Почему же тогда наука и ее картографический язык — математика — считаются трудными для изучения? Я считаю, что это происходит не потому, что они настолько сложны, а скорее потому, что они на удивление просты, но очень сильно отличаются от обычного, здравого человеческого .
Моими любимыми примерами ранней науки и замечательной общей метафорой о том, чем занимается наука являются попытки точного картографирования, которое было начато греками и потеряно впоследствии на тысячи лет, а затем возобновлено в 15 веке. К концу 1700-ых люди были в восторге от того, что могли купить карманный глобус «мира таким каким он выглядит из космоса». Спустя 200 лет мы вышли в космос, вспомнили прошлое, сделали фотографии и увидели то, что уже давно определили составители карт в 18 веке.
Все научные процессы и знания носят этот характер: это попытки «увидеть» и представить вещи очень точно с разных точек зрения, которые не являются частью наших разумных догадок о мире. Мы хотим сделать невидимое видимым. Большую часть истории человечества наши теории о себе и о мире, в котором мы живем, были, в основном, построены на необоснованных убеждениях, которые служили утешительными историями. Несколько лет назад мы обнаружили новый способ видения, который позволил нам воспринимать физический мир как бы «из космоса» с гораздо меньшим количеством предрассудков. В XXI веке нам нужно не только сделать это для физического мира, но и понять наше человеческое состояние словно смотрим на него «из космоса», без каких-либо утешительных историй, но с более глубоким пониманием того, как нам бороться с нашей человеческой природой и воспитанием.
«Глобус» Средневековья.
Карта Средиземья Толкиена.
Пустыня Мохаве.
(*) Карты, как и все наши представления для идей, являются довольно произвольными и не имеют по умолчанию какие-либо внутренние требования к точности. Например, вот три карты. Первая это карта Средневековья, вторая — это карта из «Властелина колец» Толкиена, третья это карта пустыни Мохаве. Средневековая карта показывает мир таким каким люди думали мир должен был быть, эта карта включает в себя Райский сад(вверху на дальнем востоке), Средиземноморье (середину мира), которая представляет собой вертикаль “T”, Иерусалим как центр мира, присоединенный к “Т”, а сапог Италии здесь не более чем просто выпуклость. Карта Толкиена была составлена максимально подробно, чтобы помочь читателям (и вероятно автору) визуализировать выдуманный мир Хоббита и Властелина колец. Карта пустыни Мохаве была сделана в прошлом году с использованием как методов предварительной геодезии, так и спутниковых снимков, предназначенных для размещения объектов.
Важно понимать, что с точки зрения традиционной логики ни одна из этих карт не является «настоящей», поскольку ни одна из них не находится в точном взаимно однозначном соответствии со всеми деталями, с которыми эти карты пытаются сопоставить. Другими словами, каждая из этих карт это своего рода история, которая написана в основном с помощью изображений, а не слов. В пределах карты мы можем наблюдать идеальную логику — например, если Рим это север Александрии, а Париж север Рима, то Париж это север Александрии. Эта внутренняя логика отлично работает со всеми тремя картами. Математика также является своего рода системой отображения, которая задана для того, чтобы быть полностью последовательной самой по себе — на самом деле, это включает в себя создание карт вроде этих («Измерение Земли» на греческом языке — это «Геометрия»). Когда мы пытаемся соотнести карты с тем, что они должны представлять, это вызывает у нас затруднение, и мы обнаруживаем, что ни одна из этих карт не является “настоящей” в плане истины, которая должна быть заключена внутри карты. Но если бы вы попали в пустыню Мохаве, какую “ненастоящую” карту вы бы решили взять с собой? Многие особенности “ложных” карт действительно создают разницу в современном .
С нашей точки зрения, причина обучать «новому мышлению», которая набирает популярность последние 400 лет, не в том, чтобы обеспечить большим количеством технических профессий или поддерживать страну сильной или даже создавать лучших граждан. Все это хорошие результаты, которые являются побочными продуктами нового , но реальные причины связаны с здравомыслием и цивилизацией. Если карты в наших головах не похожи на то, что находится за их пределами, то мы в лучшем случае «безумны» (unsane), как говорил Альфред Коржибский. Наше определение настоящего безумия заключается в том, что когда карты в наших головах по каким бы то ни было причинам становятся так непохожи на то «что за пределами» (включая то, что находится в картах других людей) это заметно и иногда опасно. Поскольку мы не можем сделать карты в точности правильными, мы всегда немного безумны по отношению к физическому миру. Поскольку наши фактические внутренние карты не могут быть напрямую разделены, мы еще более безумны по отношению к сопоставлениям карт этого мира друг с другом, включая нас самих. Потому что мы думаем в рамках наших внутренних карт — своего рода театральное представление наших убеждений перед нами — не будет преувеличением сказать, что мы живем не в реальности, а в бредовом, характеризующемся галлюцинациями сне, который нам нравится называть «реальностью». Мы определенно хотим построить «наименее ложную» версию этой реальности, насколько это возможно!
Цивилизация — это не состояние, которое может быть достигнуто и не само путешествие, это способ путешествовать. Для меня самая интересная и замечательная, даже удивительная, вещь о науке заключается в том, что она создается нами, хотя мы — существа, в головах у которых есть только разные истории, которые скорее должны вызвать у нас желание возглавлять саблезубых тигров нежели разбираться в многовековых изменениях климата. Но процесс научного может справляться со многими нашими неспособностями мыслить и другими недостатками в достаточно сильной манере, чтобы придумывать более точные отображения более сложных частей нашей вселенной. Вот почему нам нужно помочь детям этого мира научиться делать это.
Но почему же тогда наука и ее картографический язык — математика — считаются трудными для изучения? Я считаю, что это происходит не потому, что они настолько сложны, а скорее потому что они на удивление просты, но очень сильно отличаются от обычного, здравого человеческого . Наука и математика вырабатывают совершенно необычную точку зрения о том, «что там?» и что это значит, чтобы заявить о том, что знания об этом являются основным процессом обучения науке. Один из способов взглянуть на это заключается в том, что часть того, что нужно изучать, это новый вид здравого смысла — Алан Кромер называет это «противоречащим здравому смыслу» (uncommonsense).
И подобному тому как это не требует ничего более чем нормальный ум для изучения идей, это также не требует каких-либо крупных затрат, хотя многие люди любят оправдываться тем, что «они не обучают науке, потому что у них нет компьютеров, научного оборудования, книг и т.д.» Науке сейчас около 400 лет, а персональные компьютеры у нас есть около 20 лет, поэтому около 380 лет наука и математика изучались без использования высоких технологий. Некоторые самые важные открытия были сделаны до индустриальной революции с использованием очень малого количества оборудования.
Я думаю, что, в основном, вне зависимости от финансирования, нам не хватает взрослых, которые понимают науку и хотят работать с людьми и нам также не хватает учителей. Позор моей профессии! Большинство из нас остаются в лабораториях вдали от детей, родителей, учителей и школ. Как мы можем обучить науке «без денег»? Прежде всего, мы должны научиться наблюдать и интересоваться явлениями некатегорическим образом, то есть мы не хотим отказываться от вещей, названия которых мы только узнали — большинство вещей становятся почти невидимыми после того, как мы узнаем их и вспоминаем их названия. Поэтому мы должны найти способы «сделать невидимое видимым», чтобы избежать «преждевременного распознавания». Наука повсюду вокруг нас и многое может быть выявлено путем более тщательного изучения того, что, по нашему мнению, мы видим.
Один из способов сделать это — научиться рисовать. Как отмечает Бетти Эдвардс («Правополушарное рисование»), учиться рисовать значит учиться видеть (в отличие от изучения распознавания). Для многих вещей нам нужно найти способы отложить быстрое распознавание в пользу более медленного замечания этих вещей.
Это несколько отличается от «художественной части» изобразительного искусства тем, что мы стараемся в основном выражать визуальные детали того «что есть», а не то, как мы к этому относимся, но не все так однозначно. Как однажды заметил мой дедушка в статье, написанной им для Saturday evening о том, может ли фотография быть искусством: «Искусство появляется, когда мы трудимся с определенной целью; то есть, когда мы освобождаемся от действий, которые являются просто механическими». Чувства проявятся в любом из наших тщательно сделанных творений.
Другим хорошим примером «высокой оценки низкой стоимости» является измерение окружности велосипедной шины для проекта 5-го класса. Большая часть философского золота в науке находится в этой замечательной деятельности. Ученики использовали разные материалы и получали разные ответы, но были совершенно уверены, что там был точный ответ в сантиметрах (отчасти потому, что обучение побуждает их давать точные, а не реальные ответы). Один из учителей тоже так подумал, потому что на стороне шины было указано 20 в диаметре. Учитель «знал», что длина окружности равняется числу пи умноженному на диаметр, что число пи равняется 3,14, а дюймы конвертируются в сантиметры в отношении 2,54 и все это умножается, чтобы получить точное измерение длины окружности у шины = 159,512 см. Я предложил им измерить диаметр и они обнаружили, что он на самом деле равен 19 целых и ¾ (шина была не надута). Это был шок поскольку все они привыкли верить тому, что написано и идея провести независимый тест, чтобы проверить правильность написанного просто не пришла им в голову.
Это привело к вопросам о сдутии шины под определенным давлением, но все равно большинство считало, что есть точная длина окружности. Затем один из нас связался с производителем шин (который оказался корейцем) и было много интересных и увлекательных переписок между нами пока не нашелся инженер, который написал в ответ, что они фактически не знают длину окружности или диаметр шины. Они прессуют их и разрезают до длины равной 159,6 см ± 1 мм!
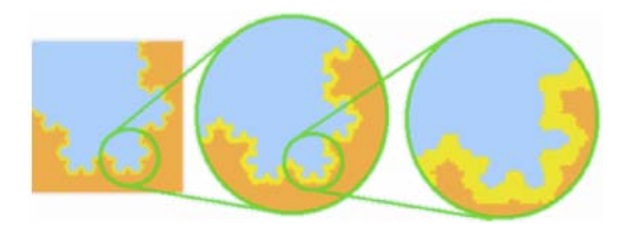
Это действительно шокировало и впечатлило детей — производитель шины даже не знал ее диаметра или длину окружности! — и это заставило их думать в более глобальных масштабах. Может быть невозможно точно измерить вещи. Разве вещи не состоят из атомов? Разве атомы не колеблются? Разве атомы не состоят из вещей, которые колеблются? И так далее. Хорошая аналогия с вечным вопросом «какой длины береговая линия?» Ответ частично связан с масштабом и допуском измерения. Как доказали Мандельброт и другие ученые, заинтересованные в фракталах, длина математической береговой линии может быть бесконечной, а физика показывает нам, что физическое измерение может быть «почти» столь же длинным (что является очень большой длиной).
Существует много способов использовать мощную идею «допустимого отклонения». Например, когда дети делают свой проект по гравитации и придумывают модель, для которой гравитация приближается к объектам на поверхности Земли, им очень важно осознать, что они могут измерять только один пиксель на своих экранах компьютеров и что они также могут делать небольшие промахи. Если они будут зациклены на точности измерений, то упустят из вида, то что происходит — равномерное ускорение. Так что они должны быть терпимы к маленьким ошибкам. С другой стороны, они должны быть достаточно бдительными касательно несоответствий, которые разнятся с типичными погрешностям измерения. Исторически так сложилось, что Галилей не мог точно измерить, как катятся шарики по наклонной плоскости, а Ньютон не знал, что на самом деле делает орбита планеты Меркурий, когда смотрел на нее.
В 2004 году исполнилось 400 лет с первого случая в истории, когда появилась хорошая модель того, что происходит, когда тело падает около поверхности Земли под воздействием силы тяжести. У Галилея не было домашних видеокамер, компьютеров и Squeak, чтобы придумать эту модель. Он сделал свое открытие «без денег», будучи очень усердным в отношении изучения и просто наблюдая до тех пор, пока не нашел способ скопировать то, что он видел, чтобы сопоставить это с математикой.
Как он это сделал? На этот вопрос нет абсолютно однозначного ответа, но есть много рассказов об этом, которые были собраны из заметок и трудов Галилея. Отец Галилея был профессиональным музыкантом, а Галилей обладал отличной репутацией как
музыкальный любитель, играющий на ряде инструментов, включая флейту и лютню.
Он проводил много экспериментов с наклонными плоскостями, используя шары одинакового размера из разных материалов и имеющих разные веса. Он обнаружил, что шарики того же размера, но разного веса по-видимому шли по наклонной плоскости с одинаковой амплитудой увеличения скорости независимо от угла.
Однажды он, возможно, позабавился, весело покатив мяч или два по верху своей лютни. Вы можете заметить, что лады у лютней и гитар неравномерно распределены. В какой-то момент он заметил, что клики мяча на ладах было почти одинаковы и понял, что более широкий интервал ладов компенсирует увеличение скорости мяча. Замечательная вещь в лютнях заключается в том, что в отличии от гитар их лады сделаны из того же материала из которого сделаны струны и поэтому они просто привязаны. Поэтому Галилей мог их переместить. Он начал их перемещать, пока не услышал абсолютно одинаковую последовательность кликов (в какой-то момент он, вероятно, начал связывать материал лада через его наклонную плоскость). Когда он получил совершенно одинаковые клики, он измерил расстояния и обнаружил, что увеличение скорости (ускорение) было константой!
Одним из самых важных заключений является тот факт, что существуют множество научных исследований, которые можно провести с помощью подручных материалов, если учитель понимает настоящую науку. Это один способ провести это исследование «без затрат», другой способ заключается в том, чтобы прокатить игрушечный грузовик с открытой банкой чернил по наклонной плоскости.
Не позволяйте отсутствию компьютера или оборудования замедлить работу. Наука и математика вокруг нас. Мир, в котором мы живем это обширная лаборатория, полная оборудования, если его можно заметить. Есть бесплатные общественные библиотеки даже в самых неблагополучных районах США, в которых есть книги, где написано как все это сделать: знание не стоит денег, но оно действительно требует времени, интереса и внимания.
Вы читаете эту книгу, потому что вас интересуют все эти проблемы — возможно, вы ее нашли в бесплатной публичной библиотеке вне зависимости от того, сможете ли вы сегодня позволить себе воспользоваться компьютером. Если не сможете, то все равно есть множество вещей, которые вы можете сделать подобно тому как существует много настоящей музыки, которую можно воспроизвести с детьми без формального использования каких-либо инструментов. Если вы можете позволить себе музыкальный инструмент или компьютер, тогда вы получили прекрасные усилители для ваших музыкальных, математических и научных импульсов.
Компьютер, в прямом смысле, превращает математику в явления, тем самым обеспечивая полный цикл «собрали части в целое», добавленный к «разобрали на части» природе науки. Это одно из самых важных применений компьютеров во взрослой науке и инженерии, и, следовательно, дети и взрослые крепко завязаны в одном и том же искусстве и спорте, и детский бейсбол и теннис — это настоящие версии спорта.
Дальнейшее понимание заключается в том, что диапазон и глубина конструкций, которые дети могут выполнить, могут быть значительно расширены с помощью подходящей компьютерной среды. Многие исследователи обнаружили, что дети способны к более глубоким мыслям, которые они могут легко построить: например, они могут мыслить шире касательного того, как роботы и животные могут найти свое место в мире и дети могут создать поистине тонкие и глубокомысленные программы на компьютере, которые воплощают эти идеи в жизнь таким образом, который находится далеко за пределами их возможностей, в таком возрасте они еще не могут создать физические воплощения этих идей.
Через несколько лет сами компьютеры станут почти бесплатными и станут частью действительно глобальной сети связи. И так, все материалы, описанные в этой книге, находятся в пределах досягаемости практически каждого ребенка на планете. Но нам еще нужно найти способы не забывать, что здесь действительно важно.
Самое важное различие, которое мы должны не упускать из виду находится между «заниматься настоящей наукой» и «изучать то, что уже сотворили ученые». Это похоже на разницу между «музыкой» и «оценкой музыки». Последнее предстоит сделать в обоих случаях, но оба случая требуют изучения реального процесса, чтобы понять, что на самом деле означает «знание об оценке». Например, нет никаких важных различий между тем, чтобы дать «святую книгу», полную утверждений и попросить запомнить их все и свято верить им, и тем, чтобы дать «научную книгу» полную утверждений и просить запомнить их и свято верить им. Как и с разницей между двумя значениями логики (истина и ложь) и многозначной логикой науки (множество бесценной лжи) разница между тем, что имеет в виду наука, когда говорит «мы знаем это» и тем, что имеют в виду предыдущие системы знаний, когда говорят это, не может быть еще более огромной. Когда наука заявляет о том, что она «знает» что-либо это настолько отличается от предыдущих применений, что не стоит даже пытаться использовать слово «знать», потому что на самом деле подразумевается, что: «у нас есть отличная модель карты, которая работает вот таким образом, но если разобраться не все отображается так же хорошо, как хотелось бы здесь и там, и, кстати, вот как вы можете помочь нам проверить это и провести свою собственную критику и т.д.»
Я надеюсь, что проекты, представленные в этой книге, и то, что вы прочитали до нее, убедят вас в том, что эти действия являются не просто «математикой и наукой», а глубокими, реальными и важными аспектами математики и науки. Что если бы было рассмотрено больше проблем физического мира в этом медленном, взвешенном восприятии, скептически, осторожно, мощно, в манере построения карт и моделей? Если вы считаете, что многие вещи стали бы значительно отличаться или улучшились бы в интересах всех людей, то пожалуйста, помогите детям научиться думать намного лучше, чем большинство взрослых сегодня.
Автор: Алексей
