На хабре уже много-много-много раз писали про игру «Жизнь». Совсем недавно была удивительная статья Жизнь на плоскости Лобачевского. Но игра «Жизнь» является частным случаем т. н. клеточных автоматов. Существует много других клеточных автоматов совсем не похожих на игру «Жизнь», но тем не менее очень интересных. Про некоторые из них и хочется рассказать здесь.
Начнём с того, что рассмотрим ряд клеток, в которых, кроме одной, находятся нули:
... 0 1 0 0 0 0 0 0 ...
Рассмотри следующее правило, заменяем число в клетке на сумму этого числа и соседа слева. Получим следующую серию состояний:
... 0 1 0 0 0 0 0 0 ... ... 0 1 1 0 0 0 0 0 ... ... 0 1 2 1 0 0 0 0 ... ... 0 1 3 3 1 0 0 0 ... ... 0 1 4 6 4 1 0 0 ... ... 0 1 5 10 10 5 1 0 ... ... 0 1 6 15 20 15 6 1 ...
Не сложно увидеть, что это — треугольник Паскаля. А теперь вместо обычного сложения будем использовать сложение по модулю два. Известно (и даже недавно рассказывалось в хабрастатье Треугольник Серпинского и треугольник Паскаля), что получится дискретный аналог треугольника Серпинского:
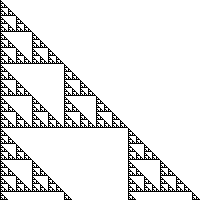
... 0 1 0 0 0 0 0 0 ... ... 0 1 1 0 0 0 0 0 ... ... 0 1 0 1 0 0 0 0 ... ... 0 1 1 1 1 0 0 0 ... ... 0 1 0 0 0 1 0 0 ... ... 0 1 1 0 0 1 1 0 ... ... 0 1 0 1 0 1 0 1 ...
Интересно? Читаем дальше!
Давать точное определение клеточного автомата здесь не имеет смысла, но полезно отметить следующие свойства клеточных автоматов: параллельность, локальность, однородность. Параллельность означает то, что обновления всех клеток происходят независимо друг от друга. Под локальностью подразумевается то, что новое состояние клетки зависит только от старого состояния клетки и её окрестности. И, наконец, однородность означает, что все клетки обновляются по одним и те же правилам.
Чтобы не связываться с бесконечными сетками, будем рассматривать клеточные автоматы на конечной четырёхугольной сетке, а чтобы не было проблем с границами, завернём сетку в тор. Две окрестности клетки имеют именные названия: это окрестность Мура — соседями являются все восемь окружающих клеток, и окрестность фон Неймана — соседями являются только ближайшие клетки слева, справа, сверху и снизу. Чтобы избежать двусмысленностей, кроме словесного описания правила преобразования состояния клетки, будет также приведена реализация функции
int transformCell(
int northWestCell, int northCell, int northEastCell,
int westCell, int centerCell, int eastCell,
int southWestCell, int southCell, int southEastCell);
Ограниченный и неограниченный рост
Итак, пусть клетки могут находиться в двух состояниях 0 — мёртвая, и 1 — живая.
Рассмотрим следующее правило: клетка становится живой, если хотя бы один из её соседей живой; клетка, однажды став живой, остаётся живой всегда. В случае окрестности Мура тело функции transformCell() будет таким:
int sum = northWestCell + northCell + northEastCell +
westCell + eastCell +
southWestCell + southCell + southEastCell;
if (sum > 0) {
return 1;
} else {
return centerCell;
}
Если поле изначально будет заполнено нулями, то живых клеток не появится, но если одну из клеток сделать живой, то из этого «зародыша» возникнет растущий квадрат из живых клеток, который в итоге заполнит поле. При этом область из живых клеток увеличивается с максимально возможной скоростью — скоростью света.


Немного изменим правило выше: вместо условия «хотя бы один из соседей живой», рассмотрим условие «в точности один из соседей живой».
int sum = northWestCell + northCell + northEastCell +
westCell + eastCell +
southWestCell + southCell + southEastCell;
if (sum == 1) {
return 1;
} else {
return centerCell;
}
Получаемая из одной клетки структура будет, во-первых, гораздо разреженней, а, во-вторых, будет иметь явный фрактальных характер.
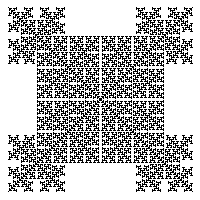

Можно вместо окрестности Мура рассмотреть окрестность фон Неймана:
int sum = northCell + westCell + eastCell + southCell;
if (sum == 1) {
return 1;
} else {
return centerCell;
}
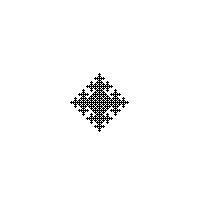


Циклические клеточные автоматы
Циклические клеточные автоматы были придуманы Дэвидом Гриффитом. Клетка может находиться в n состояниях, которые будем нумеровать числами 0, 1, ..., n – 1. Будем говорить, что состояние m является следующим за состоянием k, если m + 1 = k (mod n). Клетка из состояния m переходит в следующее состояние k, только если одна из соседних клеток имеет состояние k. Например, в случае окрестности фон Неймана преобразование запишется следующим образом:
int nextState = (centerCell + 1) % statesNumber;
if (northCell == nextState ||
westCell == nextState ||
eastCell == nextState ||
southCell == nextState) {
return nextState;
} else {
return centerCell;
}
При этом, если начать со случайно заполненного поля, могут наблюдаться три различных стадии. Первая стадия — случайное поле. Затем начинают появляться цветные области, которые будут поглощать области, заполненные случайно. Эти блоки будут «волнообразно» менять свой цвет. Далее возникают спирали, которые также называют демонами. И наконец, на третьей стадии, поле будет поглощено демонами.




Можно также рассмотреть одномерный циклический клеточный автомат:
int transformCell(int leftCell, int centerCell, int rightCell) {
int nextState = (centerCell + 1) % statesNumber;
if (nextState == leftCell || nextState == rightCell) {
return nextState;
} else {
return centerCell;
}
}

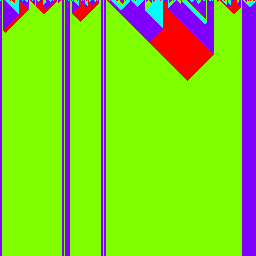
Если интересно узнать больше подробностей, то рекомендую начать с википедии Cyclic cellular automaton.
Мешанина
Пусть снова клетка может находиться в состояниях 0, 1, ..., n – 1.
Рассмотрим правило состоящее из трёх частей.
Здоровье. Если клетка находится в состоянии 0 (т. е. здорова), то она заболевает, если несколько из её соседей больны (т. е. находятся в ненулевом состоянии).
Выздоровление. Если клетка находится в состоянии n – 1, то она самовылечивается и переходит в состояние 0.
Болезнь. Иначе же состояние клетки рассчитывается как среднее состояний соседних клеток плюс некоторая константа. (Если полученное число больше чем n – 1, то новым состоянием будет n – 1.)
int sum = northWestCell + northCell + northEastCell +
westCell + eastCell +
southWestCell + southCell + southEastCell;
if (centerCell == 0) {
if (sum < 5) {
return 0;
} else if (sum < 100) {
return 2;
} else {
return 3;
}
} else if (centerCell == statesNumber - 1) {
return 0;
} else {
return Math.min(sum / 8 + 5, statesNumber - 1);
}


Отмечается, что получаемые таким образом волнообразные процессы, напоминают реакцию Белоусова – Жаботинского.
Поверхность Венеры
Это правило (как впрочем и предыдущее) я нашёл в Cellab Manual. Каждая клетка находится в состоянии 0, 1, 2 или 4. Правило имеет вид:
if (centerCell == 0) {
return 2 * ((northWestCell % 2) ^ (northEastCell % 2)) + northCell % 2;
} else if (centerCell == 1) {
return 2 * ((northWestCell % 2) ^ (southWestCell % 2)) + westCell % 2;
} else if (centerCell == 2) {
return 2 * ((southWestCell % 2) ^ (southEastCell % 2)) + southCell % 2;
} else {
return 2 * ((southEastCell % 2) ^ (northEastCell % 2)) + eastCell % 2;
}
Если начинать со случайно заполненного поля, то образуется два врезающихся друг в друга «потока»: вертикальный и горизонтальный. Через некоторое время один из «потоков» начинает преобладать. И в итоге остаётся только один.




Это небольшая часть клеточных автоматов, про которые я хотел рассказать, но я вынужден остановиться, чтобы статья не стала слишком большой. Для заинтересовавшихся дам несколько ссылок:
(1) Т. Тоффоли, Н. Марголус, Машины клеточных автоматов, М., Мир, 1991.
(2) М. Шредер, Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая, Ижевск, РХД, 2001, стр. 469--490.
(3) R. Rucker, J. Walker Cellab Manual.
Автор: mkot