
Меня всегда привлекали элементарные алгоритмы, с помощью которых можно создавать сложные паттерны. Есть в таких алгоритмах что-то фундаментальное. Один из таких алгоритмов — Perfect Shuffle. Посмотрим на его необычные свойства, а также попробуем нарисовать несколько впечатляющих фракталов с помощью этого алгоритма.
Дальше много картинок, gif-анимации и немного музыки.
Perfect Shuffle известен в среде фокусников-картежников. Называют они его Faro Shuffle. Недавно тоже захотел научиться показывать карточные фокусы. С чего начинаются фокусы? С развития ловкости рук. Повертев неделю колоду карт, освоил основные способы тасовки — «Riffle Shuffle», «Faro Shuffle», «Charlier Pass». Тренируясь делать Faro Shuffle, однажды упорядочил колоду так, чтобы все черные масти находились в начале колоды, а красные — в конце. Сделав несколько раз Faro Shuffle, обратил внимание на необычный порядок карт в колоде. Карты отложил и сел программировать.
Данный алгоритм меняет порядок элементов в массиве (перемешивает массив). Сей алгоритм элементарен:
1. Делим массив на две равные части.
2. Элементы из первой половины массива размещаем на четных позициях. Из второй — на нечетных.
Наглядно:
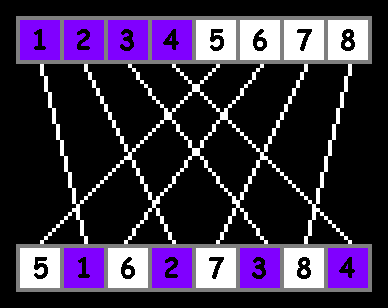
Еще наглядней:
function shuffle(array){
var half=array.length/2; //здесь мы смело делим длину массива пополам
var temparray=[];
for(var i=0;i<half;i++){
temparray[i*2]=array[i+half]; //и используем в качестве индекса
temparray[i*2+1]=array[i];
}
return temparray;
}
var array=[1, 2, 3, 4, 5, 6, 7, 8];
array=shuffle(array);
console.log(array); // [5, 1, 6, 2, 7, 3, 8, 4]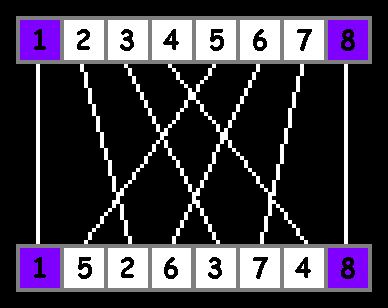
Как видим, крайние элементы остаются на своих позициях, а середина массива перемешивается тем же in-shuffle. Вариант out-shuffle далее не рассматриваем.
Кроме того, не рассматриваем вариант, когда количество элементов в массиве нечетное — последний элемент в массиве остается на своей позиции.
У алгоритма есть несколько примечательных свойств. Если перемешать массив несколько раз — через n итераций все элементы вернутся в исходную позицию! Это очевидно. Алгоритм детерминированный. Для каждого следующего состояния массива существует только одно уникальное предыдущее состояние. Количество всех возможных состояний ограничено длиной массива. Если мы будем перемешивать массив итеративно — рано или поздно мы исчерпаем возможные состояния и пойдем по второму кругу. На самом деле, это случится гораздо раньше. Количество итераций, необходимых для возврата массива в исходное состояние — меньше (или равно) количества элементов в массиве. «Меньше или равно» — все, что можно сказать о количестве итераций.
Для массива из 12-ти элементов хватит 12-ти итераций:
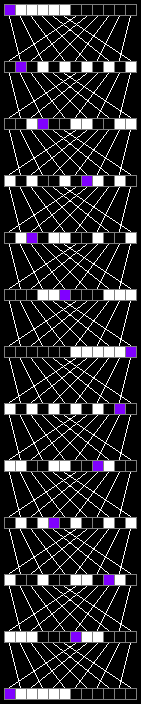
Для массива из 14-ти элементов хватит всего 4 итерации:
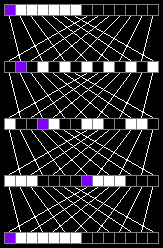
На картинке ниже (кликабельно) перемешиваем массивы с длинами от 2-х элементов до 20-ти:
Перечисленные массивы возвращаются в исходное состояние на
2, 4, 3, 6, 10, 12, 4, 8, 18, 6
итерациях. Последовательность A002326
function a002326(n){
var a=1;
var m=0;
do{
a*=2;
a%=2*n+1;
m++;
}while(a>1);
return m;
}
for(var n=1;n<11;n++){
m=a002326(n);
console.log(m);
}Построим график! На графике по оси X отметим количество элементов в массиве (деленное на 2). По оси Y — количество итераций. Белыми точками обозначим исходные состояния массивов (начало координат — левый верхний угол):

Согласитесь, точки на графике размещаются хаотично.
Еще одно необычное свойство Perfect Shuffle — после некоторого количества итераций, порядок элементов в массиве может измениться на обратный. Выше на картинке мы перемешивали массив из 12-ти элементов. Порядок элементов меняется на обратный на 6-й итерации. Нарисуем еще один график, на котором отметим массивы с обратным порядком элементов:
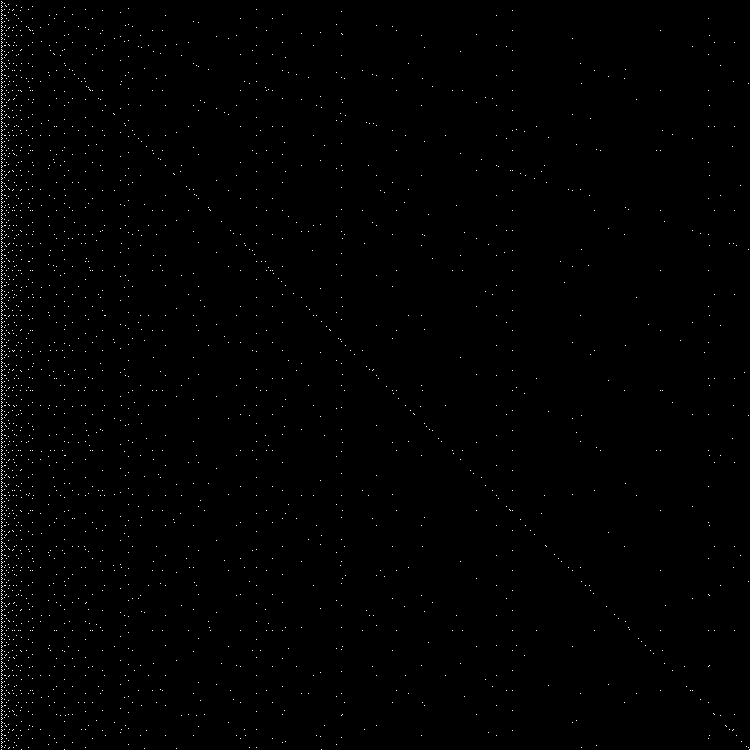
Опять же, размещение точек, не менее хаотично.
Очень интересно понаблюдать за перемещением элементов в массиве! Как элементов из первой половины массива в совокупности, так и конкретного (первого) элемента в частности.
Заполним первую половину массива нулями, вторую — единицами (далее на картинках нули — черные пиксели, единицы — белые). На картинках ниже, каждая строка (X) — состояние массива. По Y — итерации.
Несколько массивов (142-150 элементов):
288 элементов (144*2):

610 элементов:

Массив из 142-х элементов, на 55-й итерации выглядит вот так:
0011001100011001100011001100011001100111001100111001100111001100111001100110001100110001100110001100110001100110011100110011100110011100110011
Эту последовательность можем вбить сюда и посмотреть на этот массив более наглядно:
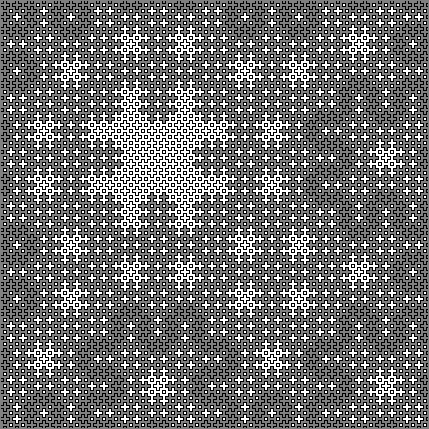





Как видим, и здесь у нас сплошной хаос. Понаблюдаем за отдельным элементом и его траекторией в массиве.
Массив 610 элементов. Заполнен только первый элемент:

Вообще, для отдельного элемента, не обязательно перемешивать весь массив. Положение конкретного элемента на следующей итерации можно посчитать по формуле:
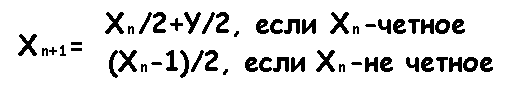
(Y — длина массива)
Первые массивы (с длинами от 2-х до 22-х):
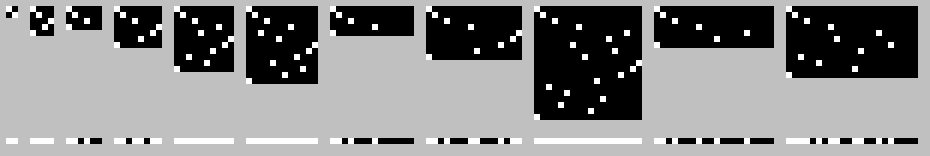
На картинке выше: в верхней части картинки массив и положение элемента на каждой итерации, в нижней части линии — все возможные положения элемента. Как видим, траектория элемента внутри массива тоже не очевидна. Чтобы окончательно в этом убедиться — из этих линий сделаем еще один график, сложив их «стопочкой»:
Черные пиксели — те позиции в массиве, в которые не попадает первый элемент при перемешивании.
На этом можно было бы остановиться, но мы пойдем еще дальше! Понаблюдаем за перемещением всех элементов в массиве. Для этого перейдем к матрицам.
Но прежде, чем переходить к перемешиванию матриц, покажу еще два фокуса с массивами.
Во второй половине массива меняем порядок элементов на обратный (на каждой итерации):

Во второй половине инвертируем элементы:
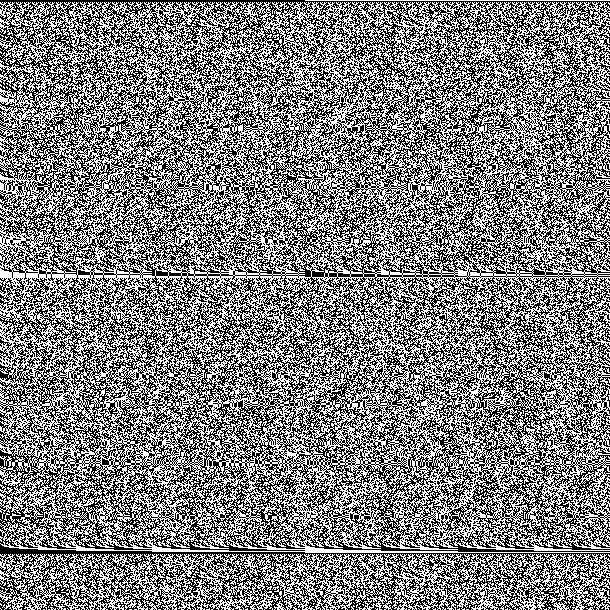
Две эти операции нам еще пригодятся.
Перейдем к матрицам!
Заполним в матрице, в первой строке — первый элемент, во второй — второй и т.д. Другими словами, нарисуем диагональ:

Перемешаем с помощью Perfect Shuffle столбики в матрице. Так мы сможем посмотреть, куда попадают все элементы после перемешивания. Матрица 80х80:

Тут явно не хватает еще одной диагонали:

Очень любопытный муар получается. Матрица 242х242 с 27 по 35 итерацию:

Ну и если уже начали перемешивать столбцы в матрице с помощью Perfect Shuffle — почему бы не перемешать и строки?
Немного модифицируем нашу функцию:
function shufflecr(array){
var half=array.length/2;
var temparray=[];
for(var x=0;x<half;x++){
temparray[x*2]=[];
temparray[x*2+1]=[];
for(var y=0;y<half;y++){
temparray[x*2][y*2]=array[x+half][y+half];
temparray[x*2+1][y*2]=array[x][y+half];
temparray[x*2][y*2+1]=array[x+half][y];
temparray[x*2+1][y*2+1]=array[x][y];
}
}
return temparray;
}Делим матрицу на 4 части. Перемешиваем столбцы. Перемешиваем строки. Получаем новую матрицу. Наглядно:
Диагонали перемешиваются довольно скучно:

Может даже показаться, что в функции где-то ошибка и матрица не перемешивается. Сдвинем диагонали на один пиксель вправо:

Замечательно. Функция работает, матрица перемешивается. Правда опять же довольно скучно. Попробуем заполнить матрицу каким-то паттерном. В рандомном месте нарисуем квадрат:
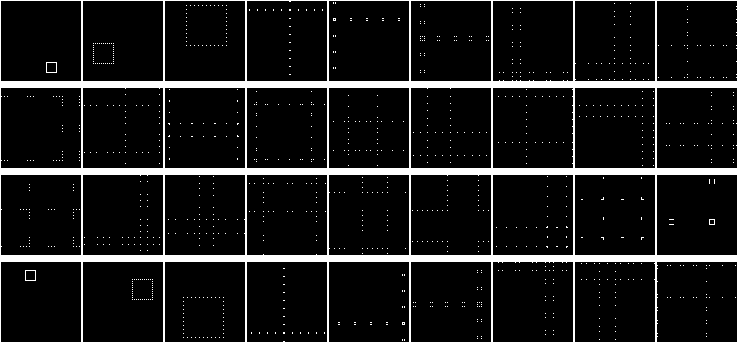
Размер матрицы 80х80 выбрал не случайно. При перемешивании массива длиной 80 элементов, на 27-й итерации порядок элементов меняется на обратный.
Подвигаем этот квадрат!
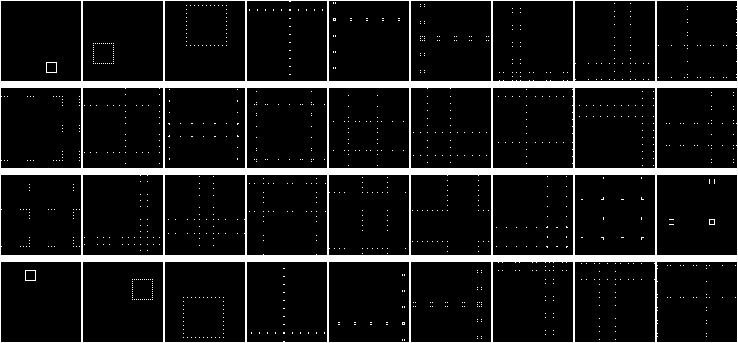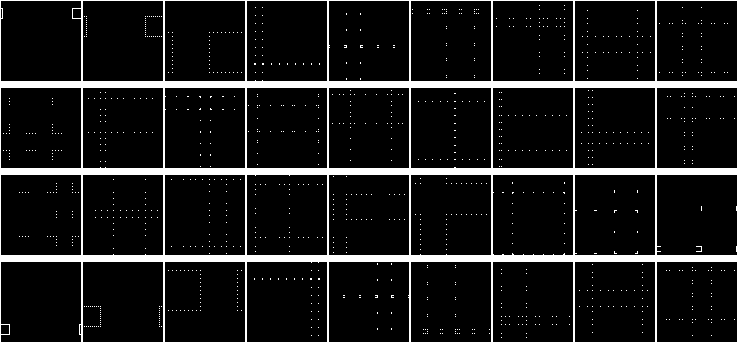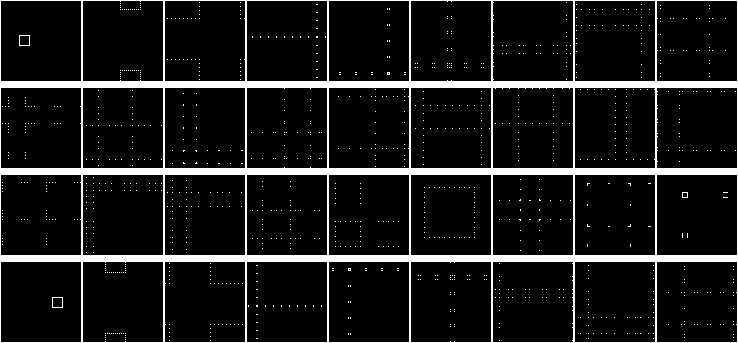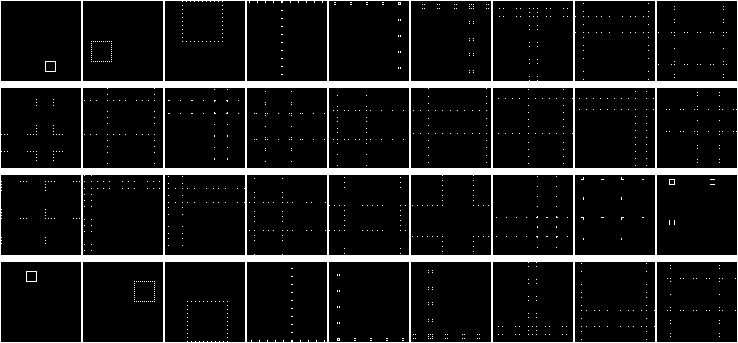
Тут можно заметить одно очень интересное свойство, но еще лучше это свойство видно, если нарисовать окружность:
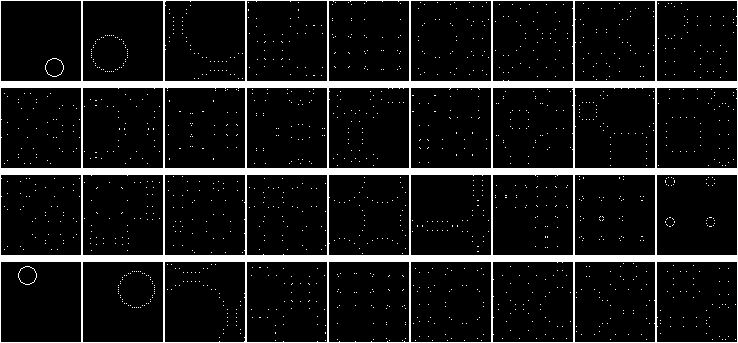
Обратите внимание на краевые эффекты. Наша матрица сворачивается в тор! Это хорошо видно на второй итерации.
Подвигаем:

Выше мы перемешивали массив и получили несколько замечательных картинок. Одна из них (144*2):

Ее тоже запишем в матрицу и перемешаем:

Или даже так. Возьмем исходный паттерн:

И оставим на нем пиксели с координатами x*4+i, y*4+j. Для i=2, j=2:
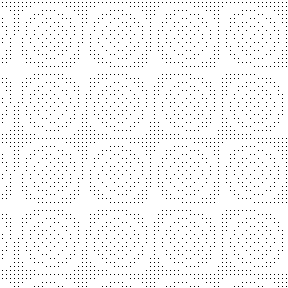
Уберем пустые столбцы и строки:

Для других i и j (фактически сделали perfect unshuffle — разделили матрицу на 16 частей):

Знакомые паттерны! Похожие паттерны можно нарисовать с помощью тригонометрических функций z=sin(n*x/y) и z=sin(n*x*y)
График функции z=sin(3*x*y). Если z>=0 — белый пиксель. Если z<0 — черный:

z=sin(13*x*y):

Один из интересных паттернов:

Можем сделать заливку, чтобы выделить замкнутые области:

На самом деле это довольно круто! Можем взять такой шаблон:

И немного сжать его осликом:
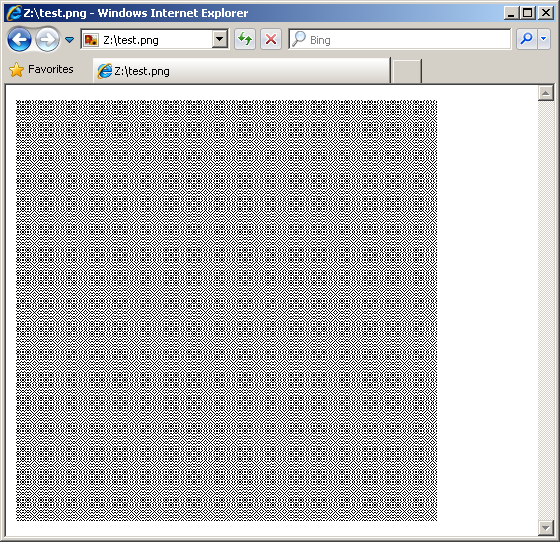
Получили знакомый паттерн.
Можно поиграться с другими шаблонами:

Сжали осликом:
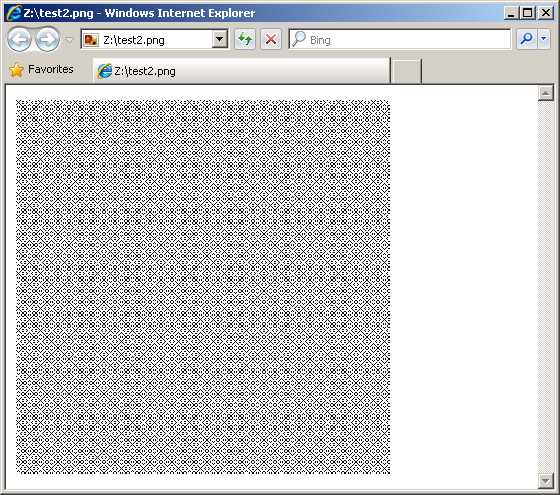
Вспомним о фокусах (изменение порядка элементов на обратный и инвертирование).
Изменение порядка элементов дает очень интересные паттерны! Один из них:

С заливкой:

Другие паттерны не менее интересны, но на них останавливаться не будем. Гораздо интересней понаблюдать за инвертированием.
Для этого эксперимента нам хватит пустой матрицы. Разделим ее на 4 части. Две из них инвертируем. Перемешаем. На первой итерации ничего необычного:

А вот дальше появляются любопытные паттерны:

Чтобы разобраться, откуда берутся эти паттерны, вернемся еще раз к массивам. До этого мы использовали матрицы и массивы фиксированной длины. Попробуем немного изменить подход — длину будем увеличивать постепенно:
1. Создадим массив из n элементов.
2. Сделаем его копию.
3. Перемешаем копию с оригиналом с помощью Perfect Shuffle. Получили массив из n*2 элементов.
4. Вернемся к шагу 2.
Копию каждый раз будем инвертировать.
Начнем с массива из двух элементов — 1 и 0
10 — исходный массив
10, 01 — массив и инвертированная копия
0110 — смешали
0110, 1001 — массив и инвертированная копия
10010110
10010110, 01101001
0110100110010110
… и т.д.
Получили последовательность Морса — Туэ (A010060) — простейший фрактал!
И обратно к матрицам. Вот тут начинается чистое искусство. До этого мы делили матрицу на 4 части и перемешивали эти части. Попробуем копировать матрицу, производить над копиями некоторые элементарные действия и перемешивать оригинал с копиями.
С матрицами можем произвести 15 элементарных действий. Действие 0 — матрица без изменений. Действия 1-7 — разные способы вращения матрицы. Действия 8-15 — инвертирование. Наглядно:

В качестве примера, произведем над копиями действия 0, 0, 7, 7. Действие 7 — поворот матрицы на 90°.
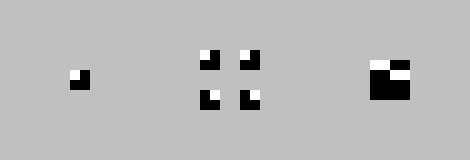
Следующая итерация:
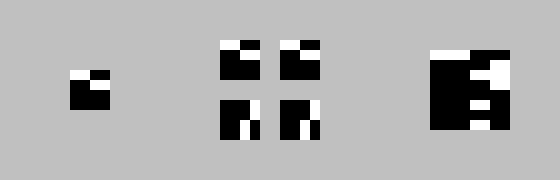
… восьмая итерация:
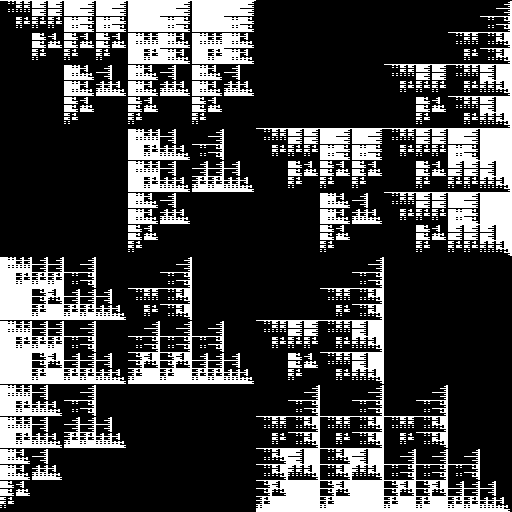
Очень необычный фрактал получился.
Действия 0, 0, 7, 7. Первая итерация:
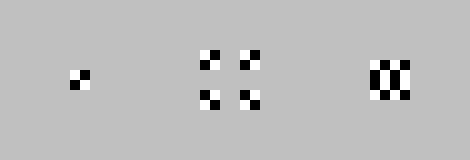
Вторая итерация:
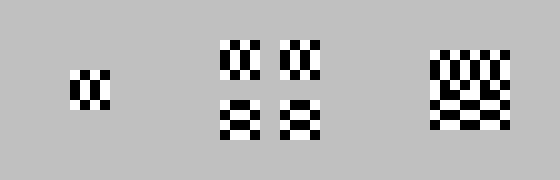
Восьмая:

А теперь два фокуса.
Накладываем сверху копию картинки с прозрачными белыми пикселями, копию поворачиваем на 90°:
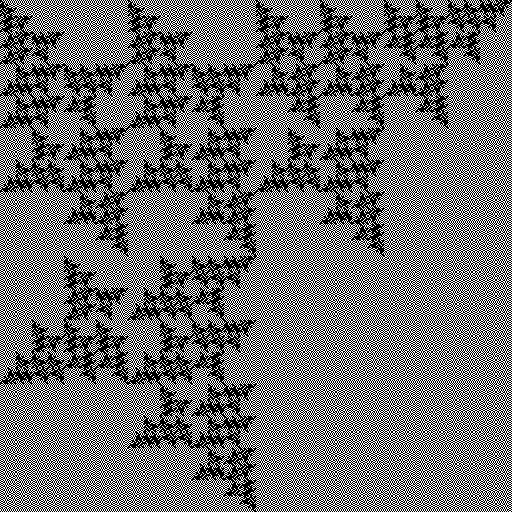
Копия повернута по вертикали:

Комбинируя перечисленные действия, можно нарисовать 16^4=65536 фракталов. Некоторые из них:
Нарисованы за 6 итераций. Картинки кликабельны (8 итераций).


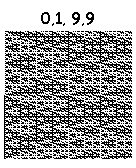


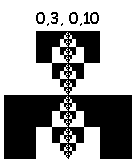
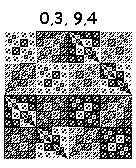
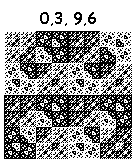

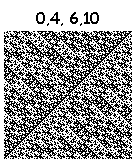
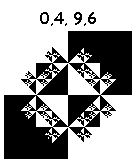

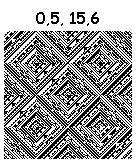
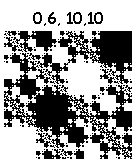




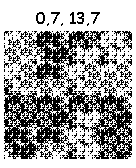


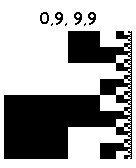
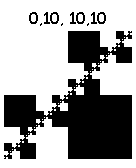


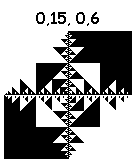

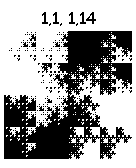



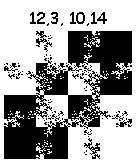
А вот эти тянут на шедевр:
15, 5, 9, 5:
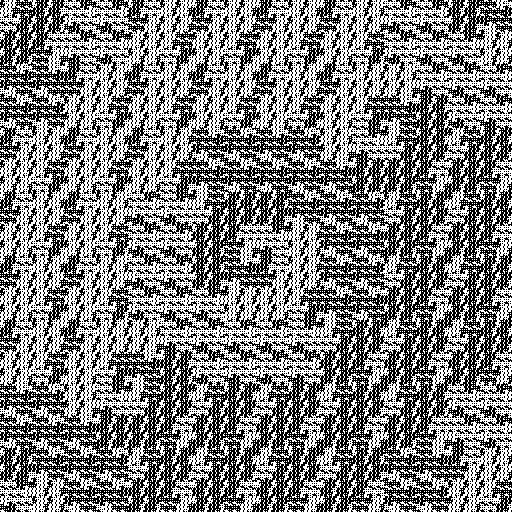
3, 5, 9, 5:
13, 7, 11, 11:

0, 0, 7, 13:
1, 1, 4, 14:

Другие фракталы можно нарисовать здесь
Вот такие «карточные фокусы» получились. Думаю, на этом можно временно остановиться (можно перемешивать трехмерные матрицы, но об этом в другой раз).



Автор: xcont







