Криптоалгоритмы. Классификация с точки зрения количества ключей

На Хабрахабре уже порядка 1000 статей так или иначе связанные с шифрованием, но иногда возникает ситуация, когда быстро нужна информация по тому или иному алгоритму.

Вместо предисловия

Изначально это должен был быть цикл из 3-х публикаций, но вовремя публикации первой и второй в комментариях мне было предложено сделать одну общую статью.
К сожалению, потребовалось больше времени, но теперь представляю Вам список из порядка 50 криптоалгоритмов, который представляет собой справочник с кратким описанием алгоритмов, а также местами их реализацией.

Часть алгоритмов довольна известна, часть является откровенной экзотикой. Но это именно те алгоритмы показались мне интересны. Возможно где-то акцент сделан не на привычные всем вещи., но как говорится на вкус и цвет все фломастеры разные. И которые так или иначе изучались в профильном ВУЗе и по которым чаще всего требовалась информация. Так сказать краткий конспект студента.

Отдельная благодарность apashkova за помощь и редактуру.
Заранее благодарю, за отзывы и предложения.

Типизация КА

Итак, представляю вам статью, в которой собраны, известные и не очень, криптографические алгоритмы. Оговоримся, что статья не претендует на новаторство, или уникальность. Скорее краткий справочник, кто-то даже назовет это прикроватным чтивом. Существуют различные классификации криптоалгоритмов, например, такая:

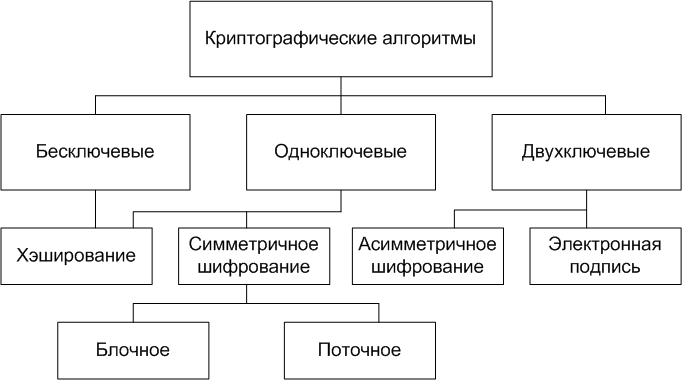
Для удобства я буду использовать деление на группы по количеству ключей:

1. Бесключевые КА — не используют в вычислениях никаких ключей;
2. Одноключевые КА — работают с одним ключевым параметром (секретным ключом);
3. Двухключевые КА — на различных стадиях работы в них применяются два ключевых параметра: секретный и открытый ключи.

Бесключевые КА

md2/4/5/6

MD2 — криптографическая хеш-функция, разработанная Рональдом Ривестом в 1989 году, и описанная в RFC 1319. На входе сообщение произвольный длины. Размер хеша — 128 бит.

Как писал в свое время braindamagedman о MD5 и MD6:

Алгоритм MD5 имел некогда большую популярность, но первые предпосылки взлома появились еще в конце девяностых, и сейчас его популярность стремительно падает.

Алгоритм MD6 — очень интересный с конструктивной точки зрения алгоритм. Он выдвигался на конкурс SHA-3, но, к сожалению, авторы не успели довести его до кондиции, и в списке кандидатов, прошедших во второй раунд этот алгоритм, отсутствует.

Tiger

Криптографическая хеш-функция, разработанная Росом Андерсоном и Эли Бихамом в 1995 году. Tiger был предназначен для особенно быстрого выполнения на 64-разрядных компьютерах. Tiger не имеет патентных ограничений, может использоваться свободно как с эталонной реализацией, так и с её модификациями. Размер значения хеша — 192 бита (Tiger/192), хотя имеются также более короткие версии для совместимости с SHA-1 (Tiger/160) и с MD4, MD5, RIPEMD, Snefru (Tiger/128). Скорость работы — 132 Мбит/с (проверено на одном процессоре Alpha 7000, модель 660). На современных процессорах значительно быстрее (даже при тесте на 32-битном AMD Sempron 3000+ скорость около 225 Мбит/с).
Так же была реализована Вторая версия Tiger2 —отличается от основной только другим алгоритмом добавления битов, сходным с MD5/SHA-1. Для Tiger2 доступны тестовые векторы.

Sha-1/2

Алгоритм криптографического хеширования. Описан в RFC 3174. Для входного сообщения произвольной длины (максимум 22^64-1 бит, что примерно равно 2 эксабайта) алгоритм генерирует 160-битное хеш-значение, называемое также дайджестом сообщения. Используется во многих криптографических приложениях и протоколах. Также рекомендован в качестве основного для государственных учреждений в США. Принципы, положенные в основу SHA-1, аналогичны тем, которые использовались Рональдом Ривестом при проектировании MD4.

SHA-3

Алгоритм хеширования переменной разрядности, разработанный группой авторов во главе с Йоаном Дайменом, соавтором Rijndael, автором шифров MMB, SHARK, Noekeon, SQUARE и BaseKing. 2 октября 2012 года Keccak стал победителем конкурса криптографических алгоритмов, проводимым Национальным институтом стандартов и технологий США. 5 августа 2015 года алгоритм утверждён и опубликован в качестве стандарта FIPS 202. В программной реализации авторы заявляют о 12,5 циклах на байт при выполнении на ПК с процессором Intel Core 2. Однако в аппаратных реализациях Keccak оказался намного быстрее, чем все другие финалисты. Алгоритм SHA-3 построен по принципу криптографической губки.

Ripemd

Криптографическая хеш-функция, разработанная в Католическом университете Лувена Хансом Доббертином (Hans Dobbertin), Антоном Босселарсом (Antoon Bosselaers) и Бартом Пренелом (Бартом Пренелем). Для произвольного входного сообщения функция генерирует 160-разрядное хеш-значение, называемое дайджестом сообщения. RIPEMD-160 является улучшенной версией RIPEMD, которая, в свою очередь, использовала принципы MD4 и по производительности сравнима с более популярной SHA-1.
Существуют так же 128-, 256- 320-битные версии алгоритма, имеющие соответственные названия.

Haval

Криптографическая хеш-функция, разработанная Yuliang Zheng, Josef Pieprzyk и Jennifer Seberry в 1992 году. Для произвольного входного сообщения функция генерирует хеш-значение, называемое дайджестом сообщения, которое может иметь длину 128, 160, 192, 224 или 256 бит. Количество итераций — переменное, от 3 до 5. Количество раундов на каждой итерации — 32. Является модификацией MD5.

Теперь пришло время одноключевых КА.

Rijndael

Так же известный как Advanced Encryption Standart – симметричный алгоритм блочного шифрования. Размер одного блока. 128 бит, ключи 128/192/256, принят стандартом правительством США по результатам конкурса AES.
Пришел на смену алгоритму DES (о нем чуть позже). Спецификация была опубликована 26 ноября 2001 год. 26 мая 2002 был объявлен стандартом шифрования. По состоянию на 2009 год является одним из самых распространенных алгоритмов симметричного шифрования.
Интересным факт, 128 ключ обеспечивает 340 андециллионов возможных комбинаций.

DES

Алгоритм для симметричного шифрования, разработанный фирмой IBM и утверждённый правительством США в 1977 году как официальный стандарт (FIPS 46-3). Размер блока для DES равен 64 бита. В основе алгоритма лежит сеть Фейстеля с 16-ю циклами (раундами) и ключом, имеющим длину 56 бит. Алгоритм использует комбинацию нелинейных (S-блоки) и линейных (перестановки E, IP, IP-1) преобразований. Для DES рекомендовано несколько режимов:

• ECB (англ. electronic code book) — режим «электронной кодовой книги» (простая замена);
• CBC (англ. cipher block chaining) — режим сцепления блоков;
• CFB (англ. cipher feed back) — режим обратной связи по шифротексту;
• OFB (англ. output feed back) — режим обратной связи по выходу.
• Прямым развитием DES в настоящее время является алгоритм Triple DES (3DES). В 3DES шифрование/расшифровка выполняются путём троекратного выполнения алгоритма DES.

MMB-шифр

От англ. modular multiplication-based block cipher — модульный блочный шифр, использующий умножение) — блочный алгоритм шифрования, основанный на операции умножения в конечной группе.
Блочный шифр, основанный на операции умножения в конечной группе (MMB) представляет собой блочный шифр, разработанный Йоан Дайменом в 1993 году как улучшение шифра IDEA. Основное новшество этого шифра заключается в использовании циклического умножения в группе Z2n−1. Создатели шифра предлагали сделать n=32, таким образом умножение будет производиться в группе Z4294967295. Также стоит отметить, что длина слов, с которыми будут производиться операции, равна n, то есть 32 в данном случае. Основная цель, которая преследовалась при создании этого шифра — создать шифр, устойчивый к дифференциальному криптоанализу. Недостатки в ключевом расписании были обнаружены Эли Бихамом, что, в комбинации с тем фактом, что шифр не был защищён от линейного криптоанализа, привело к использованию других шифров, например, 3-Way шифра.

BaseKing

В криптографии BaseKing — блочный шифр, разработанный в 1994 году Йоаном Дэменом (Joan Daemen).
Он очень тесно связан с 3-WAY; действительно, они — варианты той же самой общей техники шифрования.
У BaseKing размер блока 192 битов, что в два раза длиннее, чем 3-WAY. Длина ключа — также 192 бита.
В диссертации Дэемен представил обширную теорию блочного шифра, как довольно общий алгоритм шифра, составленный из многих обратимых преобразований, которые могут быть выбраны со значительной свободой. Он обсудил безопасность этой общей схемы против известных нападений, и дала два определённых примера шифров, состоящих из специфических выборов для переменных параметров. Эти шифры 3-WAY и BaseKing. BaseKing восприимчив к тому же самому виду нападению как 3-WAY. Daemaen, Peeters, и Ван Асш также демонстрировали потенциальную уязвимость к дифференциальному анализу, наряду с небольшим количеством методов, чтобы увеличить сопротивление данного выполнения BaseKing к такому нападению.

NOEKEON

Семейство из двух блочных шифров, разработанных Йоаном Дайменом, Michaël Peeters, Gilles Van Assche и Винсентом Рэйменом и представленных в исследовательском проекте NESSIE. Два шифра представляют собой NOEKEON в прямом режиме (direct mode) и в косвенном режиме (indirect mode). Отличаются режимы только процедурой расширения ключа.
Длина ключа в NOEKEON равна 128 битам. В каждом раунде NOEKEON использует последовательность преобразований, обратных самим себе, которые с легкостью могут быть реализованы в аппаратном или программном обеспечении, причем даже в таком, где существует возможность атаки по сторонним каналам. Шифр является компактным в реализации на различных языках программирования, быстро работает на различных аппаратных средствах и является очень эффективным в широком диапазоне платформ. Однако, NOEKEON не отвечал требованиям Wide Trail Design Strategy, что показал криптоанализ, проведенный Ларсом Кнудсеном и Håvard Raddum в апреле 2001. Кнудсен и Raddum показали, что на данный шифр возможна атака на основе связанных ключей, из-за чего шифр не прошел отбор в проекте NESSIE.
На рассмотрение в рамках конкурса NESSIE были приняты оба режима алгоритма Noekeon. Оба режима оказались подвержены атаке на основе связанных ключей, которую предложили криптологи Ларс Кнудсен и Håvard Raddum в своей работе. Кроме того, ими же было доказано, что критерии создания таблиц замен в операции Gamma не способствуют высокой криптостойкости алгоритма: при генерации таблицы замен результирующий алгоритм с вероятностью примерно 86 % окажется подвержен линейному и/или дифференциальному криптоанализу. Также было показано, что с большой вероятностью возможно найти связанные ключи. Этих причин оказалось достаточно для невыхода алгоритма Noekeon во второй раунд конкурса.

DFC

Decorrelated Fast Cipher — блочный симметричный криптоалгоритм, созданный в 1998 году совместно криптографами Парижской Высшей нормальной школы, Национального центра научных исследований (CNRS) и телекоммуникационного гиганта France Telecom под руководством известного криптолога Сержа Воденэ (англ.), специально для участия в конкурсе AES. Относится к семейству PEANUT (Pretty Encryption Algorithm with n-Universal Transformation) шифров.
Блочный шифр с длинного блока 128 бит, представляющий 8-ми раундовую Сеть Фейстеля. Используется 64-битовая функция шифрования с восемью различными раундовыми ключами по 128 бит, получаемыми из одного исходного ключа шифрования. Каждый раунд функция шифрования использует левую половину исходного текста (блока) и два 64-битных ключа, являющихся половинами соответствующего раундового, для получения 64-битного шифрованного текста. Полученная зашифрованная левая половина блока прибавляется к правой. Затем, согласно идее сети Фейстеля, левая и правая части блока меняются местами. Расшифровывание происходит так же, как и шифрование с использованием раундовых ключей в обратном порядке. Длина исходного ключа шифрования не ограничивается тремя фиксированными размерами, предусмотренными конкурсом AES (128, 192 и 256 битов), и может быть переменного размера от 0 до 256 бит.

DECIM

Decim — потоковый шифр на основе РСЛОС, разработанный Комом Бербаином, Оливером Биллетом, Анн Канту, Николя Куртуа, Бландином Дебре, Генри Гильбертом, Луи Губином, Алином Гуже, Луи Гранбуланом, Седериком Ларду, Марин Минье, Томасом Порнином и Эрвом Сибе. Специализирован для аппаратной реализации. Запатентован. Был представлен в проекте eSTREAM, где не прошёл дальше третьего этапа.
Самое главное требование к шифрам — устойчивость к различным видам атак. Алгебраические атаки — одна из самых серьёзных угроз безопасности потоковым шифрам. Если соотношение между комбинацией битов секретного ключа и порождённым её битом гамма является простым или легко предсказуемым, то и нахождение алгебраических зависимостей между комбинацией битов секретного ключа и битом ключевого потока (гамма) так же является простой задачей. Для усложнения соотношений между комбинацией битов секретного ключа (или комбинацией битов начального состояния РСЛОС, порождённого секретным ключом) и битов ключевого потока (гамма) используют нелинейную фильтрующую функцию от комбинации битов секретного ключа и механизмы десинхронизации между комбинацией битов секретного ключа и битами ключевого потока (гамма). Оба этих механизма (нелинейная фильтрующая функция и механизм десинхронизации между комбинацией битов РСЛОС и битами ключевого потока) являются основой работы и основным средством предотвращения криптоаналитических атак шифра Decim.
Начало работы потокового шифра Decim начинается с ввода 80-битного секретного ключа и 64-битного открытого ключа (Initialization Vector). Затем, с помощью определённых линейных комбинаций битов К и битов IV, использования нелинейной фильтрующей функции F и применения механизма выборки ABSG вычисляется начальное состояние 192 битного РСЛОС. После выполнения всех этих операций начинается генерация ключевого потока и заполнение им специального буфера BUFFER, использующегося для обеспечения непрерывной выдачи битов на выход шифра, где происходит их сложение по модулю два с двоичной последовательностью символов открытого текста.

MICKEY

Алгоритм потокового шифрования. Существует два варианта этого алгоритма — с длиной ключа 80 бит (MICKEY) и 128 бит (MICKEY-128). Он был разработан Стивом Бэббиджем и Мэтью Доддом в 2005 году с целью использования в системах с ограниченными ресурсами. Этот алгоритм имеет простую аппаратную реализацию при высокой степени защищённости. В нём используется нерегулярное тактирование сдвиговых регистров, а также новые методы, обеспечивающие достаточно большой период и псевдослучайность ключевой последовательности и устойчивость к атакам. Алгоритм MICKEY участвовал в конкурсном проекте eSTREAM, организованным сообществом eCRYPT. Текущая версия алгоритма — 2.0. Она вошла в портфолио eCRYPT, как потоковый шифр для аппаратной реализации.
Максимальная длина ключевой последовательности, полученной с помощью одной пары (K, IV) составляет 240 бит. Однако допускается получение 240 таких последовательностей при использовании одного K при условии, что IV выбирается разными для каждой новой последовательности.

SC2000

Симметричный блочный криптоалгоритм, разработанный фирмой Fujitsu и университетом г. Токио в 2000 году. В алгоритме используется 128-битный блок и ключ длиной от 128 до 256 бит (совместим со стандартом AES и поддерживает типовые длины ключа — 128/192/256). Был рекомендован комитетом CRYPTREC в 2003 году для использования государственными учреждениями Японии, однако в 2013 году был перемещён в список «кандидатов» в рекомендованные шифры. Участвовал в конкурсе Nessie, но не попал во второй раунд, хотя и показал достаточную устойчивость к атакам — причиной стала его слишком сложная структура и опасение в вероятности скрытых уязвимостей.
SC2000 — шифр со смешанной структурой: здесь используются элементы сети Фейстеля и подстановочно-перестановочной сети. Алгоритм выполняет 6.5 (для 128-битного ключа) и ли 7.5 (для ключа длиной 192—256 бит) раундов шифрования. Каждый из раундов состоит из запросов к таблице подстановки, добавления ключа и бесключевой двухраундовой сети Фейстеля.
Применяется три таблицы замены: S-Box размером 4x4 бит используется в начале каждого раунда, размером 5x5 бит и 6x6 бит — внутри сети Фейстеля.
Расширение ключа в алгоритме SC2000 выполняется в два этапа: основе секретного симметричного ключа генерируется промежуточный ключ, затем из промежуточного ключа вычисляется нужное количество фрагментов расширенного ключа.
Один раунд шифра довольно сложен и состоит из следующих операций: Входное 128-битное значение делится на 4 подблока по 32 бита, на каждый из них операцией XOR накладывается 32-битный фрагмент расширенного ключа. Выполняется операция T, которая разбивает блок данных на 32 подблока по 4 бита каждый.
Каждый 4-битный подблок проходит через таблицу подстановки S4, которая выглядит так: (2,5,10,12,7,15,1,11,13,6,0,9,4,8,3,14)
Далее блок данных разбивается на 32-битные подблоки с помощью операции T’, обратной к операции T. Выполняется наложение операцией XOR других четырёх фрагментов расширенного ключа. Значения первой пары подблоков передаются на вход функции F. В результате выполнения данной функции получаются два 32-битных значения, которые накладываются операцией XOR на два первых подблока. Первая пара подблоков меняется местами с второй парой подблоков, затем выполняется повторно прошлый шаг трансформации.

RC4

Также известен как ARC4 или ARCFOUR (alleged RC4) — потоковый шифр, широко применяющийся в различных системах защиты информации в компьютерных сетях (например, в протоколах SSL и TLS, алгоритмах обеспечения безопасности беспроводных сетей WEP и WPA).
Шифр разработан компанией «RSA Security», и для его использования требуется лицензия.
Алгоритм RC4, как и любой потоковый шифр, строится на основе генератора псевдослучайных битов. На вход генератора записывается ключ, а на выходе читаются псевдослучайные биты. Длина ключа может составлять от 40 до 2048 бит. Генерируемые биты имеют равномерное распределение.
Основные преимущества шифра:

• высокая скорость работы;
• переменный размер ключа.

RC4 довольно уязвим, если:

• используются не случайные или связанные ключи;
• один ключевой поток используется дважды.

Эти факторы, а также способ использования могут сделать криптосистему небезопасной (например, WEP).
Далее реализация Illivion.

using System;
using System.Linq;


namespace RC4_Testing
{
    public class RC4
    {
        byte[] S = new byte[256];

        int x = 0;
        int y = 0;

        public RC4(byte[] key)
        {
            init(key);
        }

        // Key-Scheduling Algorithm 
        // Алгоритм ключевого расписания 
        private void init(byte[] key)
        {
            int keyLength = key.Length;

            for (int i = 0; i < 256; i++)
            {
                S[i] = (byte)i;
            }

            int j = 0;
            for (int i = 0; i < 256; i++)
            {
                j = (j + S[i] + key[i % keyLength]) % 256;
                S.Swap(i, j);            
            }
        }

        public byte[] Encode(byte[] dataB, int size)
        {      
            byte[] data = dataB.Take(size).ToArray();              

            byte[] cipher = new byte[data.Length];

            for (int m = 0; m < data.Length; m++)
            {               
                cipher[m] = (byte)(data[m] ^ keyItem());
            }

            return cipher;
        }
        public byte[] Decode(byte[] dataB, int size)
        {
            return Encode(dataB, size);
        }
        
        // Pseudo-Random Generation Algorithm 
        // Генератор псевдослучайной последовательности 
        private byte keyItem()
        {
            x = (x + 1) % 256;
            y = (y + S[x]) % 256;

            S.Swap(x, y);

            return S[(S[x] + S[y]) % 256];
        }     
    }

    static class SwapExt
    {
        public static void Swap<T>(this T[] array, int index1, int index2)
        {
            T temp = array[index1];
            array[index1] = array[index2];
            array[index2] = temp;
        }
    }
}

RC5

Блочный шифр, разработанный Роном Ривестом из компании RSA Security Inc. с переменным количеством раундов, длиной блока и длиной ключа. Это расширяет сферу использования и упрощает переход на более сильный вариант алгоритма.
Существует несколько различных вариантов алгоритма, в которых преобразования в «пол-раундах» классического RC5 несколько изменены. В классическом алгоритме используются три примитивных операции и их инверсии:

1. сложение по модулю
2. побитовое исключающее ИЛИ (XOR)
3. операции циклического сдвига на переменное число бит.

Основным нововведением является использование операции сдвига на переменное число бит, не использовавшиеся в более ранних алгоритмах шифрования. Эти операции одинаково быстро выполняются на большинстве процессоров, но в то же время значительно усложняют дифференциальный и линейный криптоанализ алгоритма.
Шифрование по алгоритму RC5 состоит из двух этапов. Процедура расширения ключа и непосредственно шифрование. Для дешифрования выполняется сначала процедура расширения ключа, а затем операции, обратные процедуре шифрования.

Rabbit

Высокоскоростной поточный шифр впервые представленный в феврале 2003 года на 10-м симпозиуме FSE. В мае 2005, он был отправлен на конкурс eStream, целью которого было создание европейских стандартов для поточных систем шифрования.
Разработчиками Rabbit являются Martin Boesgaard, Mette Vesterager, Thomas Pedersen, Jesper Christiansen и Ove Scavenius.
Rabbit используют 128-битный ключ и 64-битный инициализирующий вектор. Шифр был разработан с целью использования в программном обеспечении, как обладающий высокой скоростью шифрования. При этом скорость шифрования могла достигать 3.7 циклов в байт(CPB) для процессора Pentium 3 и 10.5 циклов в байт для ARM7. Тем не менее, шифр также оказался быстрым и компактным при реализации в аппаратном обеспечении.
Основным компонентом шифра является генератор битового потока, который шифрует 128 битов сообщения за итерацию. Достоинство шифра в тщательном перемешивании его внутренних состояний между двумя последовательными итерациями. Функция перемешивания полностью основана на арифметических операциях, доступных на современных процессорах, то есть S-блоки подстановок и поисковые таблицы не нужны для реализации шифра.
Авторы шифра предоставили полный набор технических описаний на домашней странице Cryptico. Шифр также описан в RFC 4503. Cryptico обладала патентом на шифр, и многие годы для использования шифра в коммерческих целях требовалась лицензия. Однако, 6 октября 2008 шифр разрешили использовать для любых целей бесплатно.

NewDes

В криптографии симметричный блочный криптоалгоритм, разработанный Робертом Скотом в качестве замены стандарта DES в 1985 году с целью внедрения более надежного шифра с безопасным размером ключа — 120 бит.
NewDES, хотя и имеет производное наименование, имеет абсолютно иную структуру, значительно проще DES, легко реализуем программно и не включает побитовых перестановок, все операции производятся с байтами. Алгоритм использует таблицу замены из 256 элементов, в одном раунде производятся 8 операций сложения по модулю 2 и подстановки с использованием функции F — замен с использованием таблицы подстановок.
Ключевое расписание в первой редакции было довольно слабым и было исправлено в редакции NewDES-96. Как оказалось, алгоритм NewDES менее устойчив к криптоанализу, нежели алгоритм DES, хотя атака грубой силой на NewDES-96 практически невозможна и алгоритм в данной редакции значительно более безопасен.

Salsa20

Система поточного шифрования, разработанная Даниэлем Бернштейном (англ.) русск. Алгоритм был представлен на конкурсе «eSTREAM», целью которого было создание европейских стандартов для шифрования данных, передаваемых почтовыми системами. Алгоритм стал победителем конкурса в первом профиле (поточные шифры для программного применения с большой пропускной способностью).
Шифр Salsa20 использует следующие операции:

1. сложение 32-битных чисел;
2. побитовое сложение по модулю 2 (xor);
3. сдвиги битов.

Алгоритм использует хеш-функцию с 20 циклами. Основные её преобразования напоминают алгоритм AES.

Seal

Симметричный поточный алгоритм шифрования данных, оптимизированный для программной реализации.
Разработан в IBM Филом Рогэвеем (англ.) (англ. Phil Rogaway) и Доном Копперсмитом (англ. Don Coppersmith) в 1993 году. Алгоритм оптимизирован и рекомендован для 32-битных процессоров. Для работы ему требуется кэш-память на несколько килобайт и восемь 32-битовых регистров. Скорость шифрования — примерно 4 машинных такта на байт текста. Для кодирования и декодирования используется 160-битный ключ. Чтобы избежать нежелательной потери скорости по причине медленных операций обработки ключа, SEAL предварительно выполняет с ним несколько преобразований, получая в результате три таблицы определенного размера. Непосредственно для шифрования и расшифрования текста вместо самого ключа используются эти таблицы.
Алгоритм считается очень надёжным, очень быстрым и защищён патентом США № 5454039 с декабря 1993 года.

Sosemanuk

Sosemanuk является новым симметричным ПО – ориентированным потоковым шифром, согласно Profile 1 «ECRYPT call for stream cipher primitives». Длина ключа колеблется от 128 до 256 бит. Начальное значение устанавливается объёмом 128 бит. Как утверждается, любая длина ключа достигает 128-битной защиты. Шифр Sosemanuk использует как основные принципы из потокового шифра SNOW 2.0, так и некоторые преобразования, выведенные из блочного шифра SERPENT. Sosemanuk нацелен на улучшение SNOW 2.0 как в смысле безопасности, так и смысле эффективности. В частности, он использует быструю IV-setup процедуру. Так же необходимо снижение числа статических данных в пользу улучшения производительности на нескольких архитектурах(платформах).
Шифр Sosemanuk использует как основные принципы потокового шифра SNOW 2.0 («Snow» – англ. «снег»), так и некоторые трансформации(преобразования), выведенные из блочного шифра SERPENT («SERPENT» – англ. «змея»). По этой причине его название должно быть связано и со змеёй, и со снегом. Однако хорошо известно, что снежных змей не существует, так как змеи либо засыпают, либо перебираются в тёплые края на время зимы. Кроме того, Sosemanuk – популярный вид спорта, распространенный среди племён Восточной Канады. Идея игры состоит в метании деревянной палки вдоль снежного берега настолько, насколько это возможно. Название происходит из наречия народов и содержит сравнение палки на снегу со змеёй. «Kwakweco-cime win» является одним из названий подобной игры, но оно не звучит соответствующе для названия шифра.

Trivium

Симметричный алгоритм синхронного потокового шифрования, ориентированный, в первую очередь, на аппаратную реализацию с гибким равновесием между скоростью работы и количеством элементов, имеющий также возможность достаточно эффективной программной реализации.
Шифр был представлен в декабре 2008 года как часть портфолио европейского проекта eSTREAM, по профилю 2 (аппаратно ориентированные шифры). Авторами шифра являются Кристоф Де Канньер и Барт Пренел.
Данный потоковый шифр генерирует вплоть до бит выходного потока из 80 бит ключа и 80 бит IV (вектора инициализации). Это — самый простой шифр проекта eSTREAМ, который показывает отличные результаты по криптоустойчивости.
Trivium включен в стандарт ISO/IEC 29192-3 в качестве легковесного потокового шифра.
Изначальное состояние Trivium представляет собой 3 сдвиговых регистра суммарной длины в 288 бит. Каждый такт происходит изменение битов в регистрах сдвига путём нелинейной комбинации прямой и обратной связи. Для инициализации шифра ключ K и инициализирующий вектор IV записываются в 2 из 3х регистров и происходит исполнение алгоритма в течение 4х288 = 1152 раз, что гарантирует зависимость каждого бита начального состояния от каждого бита ключа и каждого бита инициализирующего вектора.
После прохождения стадии инициализации каждый такт генерируется новый член ключевого потока Z, который проходит процедуру XOR с следующим членом текста. Процедура расшифровки происходит в обратном порядке — каждый член шифротекста проходит процедуру XOR с каждым членом ключевого потока Z.

VMPC

Это потоковый шифр, применяющийся в некоторых системах защиты информации в компьютерных сетях. Шифр разработан криптографом Бартошем Жултаком (польск. Bartosz Żółtak, англ. Bartosz Zoltak) в качестве усиленного варианта популярного шифра RC4. Алгоритм VMPC строится, как и любой потоковый шифр на основе параметризованного ключом генератора псевдослучайных битов. Основные преимущества шифра, как и RC4 — высокая скорость работы, переменный размер ключа и вектора инициализации (от 128 до 512 бит включительно), простота реализации (буквально несколько десятков строк кода).
Основа шифра — генератор псевдослучайных чисел, базой которого является односторонняя необратимая функция VMPC (англ. Variably Modified Permutation Composition).

FROG

Алгоритм симметричного блочного шифрования c неортодоксальной структурой, один из участников американского конкурса AES, разработка костариканской компании TecApro Internacional.
Алгоритм FROG был создан в 1998 тремя специалистами компании Tecnologia Apropriada (ТесАрго) из небольшого латиноамериканского государства Коста-Рика (неизвестного ранее своими разработками в области криптографии): Дианелосом Георгоудисом (Dianelos Georgoudis), Дамианом Jlepy (Damian Leroux) и Билли Симоном Чавесом (Billy Simon Chaves).
Заявленный на конкурс вариант шифра соответствует требованиям AES, имея блок, равный 128 бит и ключ длиной 128, 192 или 256 бит. Сам алгоритм, теоретически, допускает ключи длиной от 40 до 1000 бит.
Шифр FROG выставила на конкурс международная компания TecApro Internacional, зарегистрированная в Коста-Рике. Разработчики алгоритма — Д. Георгудис (D. Georgoudis), Д. Леру (D. Leroux) и Б. Шаве (B. Chaves) — люди, мягко говоря, мало известные в криптографическом мире. Как утверждают авторы, FROG — это «новый шифр с неортодоксальной структурой». Основу стойкости шифра составляет секретный внутренний ключ сложной конструкции, сами же операции шифрования/дешифрования чрезвычайно просты.
В августе команда TWOFISH (Вагнер, Фергюсон и Шнайер) показали, что ключ шифра FROG можно вскрывать при трудозатратах около 257.
Что же касается стойкости шифров, то этот показатель проверить значительно сложнее. В ходе этапа предварительной оценки первого круга на web-сайте НИСТ и непосредственно на конференции AES2 было представлено значительное количество криптоаналитических результатов, так или иначе «подмочивших» репутацию практически всех шифров-кандидатов. Однако, если не говорить о явных аутсайдерах LOKI, FROG, MAGENTA и HPC, то никаких очевидных слабостей в алгоритмах не обнаружено.

NUSH

Блочный алгоритм симметричного шифрования, разработанный Анатолием Лебедевым и Алексеем Волчковым для российской компании LAN Crypto.
NUSH имеет несколько различных вариантов, имеющих разный размер блока (64, 128, 256 бит), различное число раундов (в зависимости от размера блока равно 36, 128 или 132 раунда) и использует длину ключа в 128, 192 или 256 бит. Алгоритм не использует S-блоки, а только такие операции, как AND, OR, XOR, сложение по модулю и циклические сдвиги. Перед первым и после последнего раунда проводится «отбеливание» ключа.
Данный алгоритм был выдвинут в проекте NESSIE, но не был выбран, так как было показано, что линейный криптоанализ может быть эффективнее, чем атака перебором.
На основе алгоритма шифрования можно построить и другие алгоритмы. Несколько из них изложены в настоящей статье.

REDOC

Симметричный блочный криптоалгоритм, разработанный Майклом Вудом в 1990 году для компании Cryptech и получивший наименование REDOC II. Все операции — подстановки, перестановки, XOR выполняются с байтами что позволяет его эффективно реализовать программно. Алгоритм использует зависимые от ключа и исходного открытого текста наборы таблиц (S-блоков), используя меняющиеся табличные функции. Алгоритм отличает использование масок, т.е. чисел, получаемых из ключевой таблицы. Маски используются для выбора таблиц конкретной функции конкретного раунда. При этом используется как значение маски, так и значение данных.
Наиболее эффективным способом вскрытия ключа считается грубая сила, для достижения цели потребуется 2160 операций. Практически единственным эффективным криптоанализом было вскрытие одного из раундов алгоритма Томасом Кузиком, но расширить вскрытие на дальнейшие раунды не удалось. С помощью 2300 открытых текстов был проведен криптоанализ одного из раундов Шамиром и Бихамом, после 4 раундов были получены 3 значения маски, однако успехов как таковых это не принесло и на данный момент алгоритм считается криптостойким.
Существует также значительно упрощенная версия алгоритма — REDOC III, созданный Майклом Вудом. Используется 80-битный блок, длина ключа переменна, может достигать 20480 битов. Перестановки и подстановки исключены, все операции над блоком и ключом основаны лишь на применении XOR, за счет чего значительно увеличена скорость шифрования в ущерб стойкости к дифференциальному криптоанализу. Основой алгоритма являются генерированные на основе секретного ключа 256 10-байтовых ключей, и полученные на основе XOR 128 10-байтовых ключей два 10-байтовых блока маски. Для успешного восстановления обеих масок алгоритма REDOC III требуется 223 открытых текстов. Этот алгоритм несложен и быстр. На 33 мегагерцовом процессоре 80386 он шифрует данные со скоростью 2.75 Мбит/с. Криптографическая система REDOC II способна шифровать 800 кбит/с при тактовой частоте 20 МГц.
Алгоритм REDOC II и его упрощенная версия запатентованы в США.

3-way

Это симметричный блочный шифр с закрытым ключом, разработанный Йоаном Дайменом (Joan Daeman), одним из авторов алгоритма Rijndael (иногда называемого AES).
Алгоритм 3-Way является 11-шаговой SP-сетью. Используются блок и ключ длиной 96 бит. Схема шифрования, как и характерно для алгоритмов типа SP-сеть, предполагает эффективную аппаратную реализацию.
Вскоре после опубликования был проведён успешный криптоанализ алгоритма 3-Way, показавший его уязвимость к атаке на основе связанных ключей. Алгоритм не запатентован.

Blowfish

Криптографический алгоритм, реализующий блочное симметричное шифрование с переменной длиной ключа. Разработан Брюсом Шнайером в 1993 году. Представляет собой сеть Фейстеля. Выполнен на простых и быстрых операциях: XOR, подстановка, сложение. Является незапатентованным и свободно распространяемым.
До появления Blowfish существовавшие алгоритмы были либо запатентованными, либо ненадёжными, а некоторые и вовсе держались в секрете (например, Skipjack). Алгоритм был разработан в 1993 году Брюсом Шнайером в качестве быстрой и свободной альтернативы устаревшему DES и запатентованному IDEA. По заявлению автора, критериями проектирования Blowfish были:

1. скорость (шифрование на 32-битных процессорах происходит за 26 тактов);
2. простота (за счёт использования простых операций, уменьшающих вероятность ошибки реализации алгоритма);
3. компактность (возможность работать в менее, чем 5 Кбайт памяти);
4. настраиваемая безопасность (изменяемая длина ключа).

Алгоритм состоит из двух частей: расширение ключа и шифрование данных. На этапе расширения ключа исходный ключ (длиной до 448 бит) преобразуется в 18 32-битовых подключей и в 4 32-битных S-блока, содержащих 256 элементов. Общий объём полученных ключей равен бит или 4168 байт.

Cast

Блочный алгоритм симметричного шифрования на основе сети Фейстеля, который используется в целом ряде продуктов криптографической защиты, в частности некоторых версиях PGP и GPG и кроме того одобрен для использования Канадским правительством.
Алгоритм был создан в 1996 году Карлайлом Адамсом (Carlisle Adams) и Стаффордом Таваресом (Stafford Tavares) используя метод построения шифров CAST, который используется также и другим их алгоритмом CAST-256 (алгоритм-кандидат AES).
CAST-128 состоит из 12 или 16 раундов сети Фейстеля с размером блока 64 бита и длиной ключа от 40 до 128 бит (но только с инкрементацией по 8 бит). 16 раундов используются, когда размеры ключа превышают 80 бит. В алгоритме используются 8x16 S- блоки, основанные на бент-функции, операции XOR и модулярной арифметике (модулярное сложение и вычитание). Есть три различных типа функций раундов, но они похожи по структуре и различаются только в выборе выполняемой операции (сложение, вычитание или XOR) в различных местах.
Хотя CAST-128 защищён патентом Entrust, его можно использовать во всём мире для коммерческих или некоммерческих целей бесплатно.
CAST устойчив к дифференциальному и линейному криптоанализу. Сила алгоритма CAST заключена в его S-блоках. У CAST нет фиксированных S-блоков и для каждого приложения они конструируются заново. Созданный для конкретной реализации CAST S-блок уже больше никогда не меняется. Другими словами, S-блоки зависят от реализации, а не от ключа. Northern Telecom использует CAST в своём пакете программ Entrust для компьютеров Macintosh, PC и рабочих станций UNIX. Выбранные ими S-блоки не опубликованы, что, впрочем, неудивительно.
CAST-128 принадлежит компании Entrust Technologies, но является бесплатным как для коммерческого, так и для некоммерческого использования. CAST-256 — бесплатное доступное расширение CAST-128, которое принимает размер ключа до 256 бит и имеет размер блока 128 бит. CAST-256 был одним из первоначальных кандидатов на AES.
CAST-256 построен из тех же элементов, что и CAST-128, включая S-боксы, но размер блока увеличен вдвое и равен 128 битам. Это влияет на диффузионные свойства и защиту шифра.
В RFC 2612 указано, что CAST-256 можно свободно использовать по всему миру в коммерческих и некоммерческих целях.

e2

В криптографии, E2 является симметричным блочным шифром, который был создан в 1998 году NTT и представили на конкурс AES.
Как и другие кандидаты AES, Е2 работает на блоках 128 бит, с использованием ключа 128, 192 или 256 бит. Он использует 12-раундовом сеть Фейстеля. E2 имеет входное и выходное преобразование преобразование, как использование модульного умножения, но круглая функция сама состоит только из операцию XOR и S-коробки поиска. Сингл 8 × 8-разрядный S-бокс изготовлен из состава аффинного преобразования с дискретным возведения в степень X127 над конечным полем GF (28). NTT приняла многие из специальных характеристик Е2 в в Камелии, который по существу заменили Е2.

Twofish

Симметричный алгоритм блочного шифрования с размером блока 128 бит и длиной ключа до 256 бит. Число раундов 16. Разработан группой специалистов во главе с Брюсом Шнайером. Являлся одним из пяти финалистов второго этапа конкурса AES. Алгоритм разработан на основе алгоритмов Blowfish, SAFER и Square.
Отличительными особенностями алгоритма являются использование предварительно вычисляемых и зависящих от ключа узлов замены и сложная схема развёртки подключей шифрования. Половина n-битного ключа шифрования используется как собственно ключ шифрования, другая — для модификации алгоритма (от неё зависят узлы замены).
Twofish разрабатывался специально с учетом требований и рекомендаций NIST для AES:

1. 128-битный блочный симметричный шифр
2. Длина ключей 128, 192 и 256 бит
3. Отсутствие слабых ключей
4. Эффективная программная (в первую очередь на 32-битных процессорах) и аппаратная реализация
5. Гибкость (возможность использования дополнительных длин ключа, использование в поточном шифровании, хэш-функциях и т. д.).
6. Простота алгоритма — для возможности его эффективного анализа.

Однако именно сложность структуры алгоритма и, соответственно, сложность его анализа на предмет слабых ключей или скрытых связей, а также достаточно медленное время выполнения по сравнению с Rijndael на большинстве платформ, сыграло не в его пользу.
Алгоритм Twofish возник в результате попытки модифицировать алгоритм Blowfish для 128-битового входного блока. Новый алгоритм должен был быть легко реализуемым аппаратно (в том числе использовать таблицы меньшего размера), иметь более совершенную систему расширения ключа (key schedule) и иметь однозначную функцию F.
В результате, алгоритм был реализован в виде смешанной сети Фейстеля с четырьмя ветвями, которые модифицируют друг друга с использованием криптопреобразования Адамара (Pseudo-Hadamar Transform, PHT).
Возможность эффективной реализации на современных (для того времени) 32-битных процессорах (а также в смарт-картах и подобных устройствах) — один из ключевых принципов, которым руководствовались разработчики Twofish.
Например, в функции F при вычислении PHT и сложении с частью ключа K намеренно используется сложение, вместо традиционного xor. Это дает возможность использовать команду LEA семейства процессоров Pentium, которая за один такт позволяет вычислить преобразование Адамара (Правда в таком случае код приходится компилировать под конкретное значение ключа).
Алгоритм Twofish не запатентован и может быть использован кем угодно без какой-либо платы или отчислений. Он используется во многих программах шифрования, хотя и получил меньшее распространение, чем Blowfish.

Xtea

Блочный шифроалгоритм, призванный устранить критические ошибки алгоритма TEA. Разработчиками шифра являются Дэвид Уилер и Роджер Нидхэм (факультет компьютерных наук Кэмбриджского университета). Алгоритм был представлен в неизданном техническом отчете в 1997 году. Шифр не патентован, широко используется в ряде криптографических приложений и широком спектре аппаратного обеспечения благодаря крайне низким требованиям к памяти и простоте реализации.
Как и TEA, шифр основан на операциях с 64-битным блоком, имеет 32 полных цикла, в каждом полном цикле по два раунда Сети Фейстеля, что означает 64 раунда сети Фейстеля. Однако, число раундов для достижения лучшей диффузии может быть увеличено в ущерб производительности. Кроме того в XTEA, как и в TEA, используется 128-битный ключ, состоящий из четырех 32-битных слов K[0], K[1], K[2] и K[3]. В XTEA нет алгоритма планирования ключей в привычном понимании. Для того, чтобы определить какое из четырех слов ключа использовать в каждом раунде, в алгоритме используется константа δ = 9E3779B916. В TEA же такого распределения нет. Еще одним отличием от TEA является перестановка битовых операций, использующихся в шифре. Благодаря этим улучшениям XTEA не претерпел сильных усложнений по сравнению с TEA, но в то же время ликвидировал два основных недостатка алгоритма TEA:
каждый ключ в TEA эквивалентен трем другим, что означает, что эффективная длина ключа составляет 126 бит вместо 128, как это было задумано разработчиками;
TEA восприимчив к атакам на связанных ключах. Такая атака может потребовать всего лишь 223 выбранного открытого текста и иметь временную сложность равную 232.

Wake

Алгоритм поточного шифрования на автоматическом ключе, созданный Дэвидом Уилером (David J Wheeler) в 1993 году. Является системой шифрования со среднескоростной шифровкой блоков. При работе требуется использование таблиц повторений и наличие большого пространства состояний. В гамме шифра используются 32-битовые слова, работает в режиме CFB — предыдущее слово шифрованной последовательности служит основанием генерации следующего. Также в алгоритме используется S-блок замены, состоящий из 256 32-битных слов, что увеличивает его стойкость.
Алгоритм является нестойким к атакам по выбранному исходному тексту и атакам по подобранным шифротекстам.

Skipjack

Блочный шифр, разработанный Агентством национальной безопасности США в рамках проекта Capstone[en]. После разработки сведения о шифре были засекречены. Изначально он предназначался для использования в чипе Clipper для защиты аудио информации, передаваемой по сетям правительственной телефонной связи, а также по сетям мобильной и беспроводной связи. Позже алгоритм был рассекречен.
Skipjack являлся одной из инициатив, предложенных в рамках проекта Capstone. Руководили проектом Агентство национальной безопасности (АНБ) и Национальный институт стандартов и технологий (НИСТ), финансируемые правительством США. Официальная дата начала инициативы — 1993 год. Алгоритм шифрования был разработан в 1980 году, а первая его реализация была получена в 1987 году. Шифр был предназначен для использования в чипе Clipper, встраиваемом в защищаемое оборудование. При этом Skipjack использовался только для шифрования сообщений, а депонирование ключа для возможности последующего использования уполномоченными органами — наиболее обсуждаемый аспект использования шифра — достигалось за счёт отдельного механизма, называемого Law Enforcement Access Field.
Изначально проект был засекречен и по этой причине подвергся огромной критике. Для повышения общественного доверия и оценки алгоритма были призваны несколько академических исследователей. По причине отсутствия времени для самостоятельного тщательного исследования, эксперты сконцентрировались на изучении представленного АНБ описания процесса разработки и оценки алгоритма. В дополнение к этому они, в течение месяца, провели ряд небольших тестов. В предварительном отчете об их работе (окончательного отчета так и не последовало) указаны три заключения:

1. Принимая во внимание, что стоимость вычислительных мощностей уменьшается вдвое каждые 18 месяцев, лишь через 36 лет стоимость взлома Skipjack полным перебором сравняется со стоимостью взлома DES сегодня.
2. Риск взлома шифра с помощью более быстрых способов, включая дифференциальный криптоанализ, незначителен. Алгоритм не имеет слабых ключей и свойства комплементарности.
3. Устойчивость Skipjack к криптоанализу не зависит от секретности самого алгоритма.

Шифр был опубликован в открытый доступ 24 июня 1998 года. В августе 2016 года НИСТ принял новые принципы использования криптографических стандартов, в которых отозвал сертификацию алгоритма Skipjack для правительственных целей.
Skipjack использует 80-битный ключ для шифрования/дешифрования 64-битных блоков данных. Это несбалансированная сеть Фейстеля с 32 раундами.

Shark

Алгоритм SHARK разработан Винсентом Рид- жменом и Джоан Деймен — будущими авторами стандарта AES, правда, в соавторстве с еще тремя специалистами, представляющими Католический Университет г. Лювен, Бельгия. Это немногим более ранняя разработка, чем алгоритм Square, — SHARK разработан в 1995 г.
В алгоритме используются 128-битный ключ и 64-битный блок. Алгоритм SHARK имеет консервативные параметры и создан для замены существующих шифров с 64 битным блоком, вроде IDEA и DES.
Существует два варианта шифра SHARK: SHARK-A (англ. affine transform) и SHARK-E (англ. exor).
Существуют атаки лишь на модифицированный вариант шифра с 5 раундами. Сам алгоритм на данный момент можно считать безопасным.
Данный алгоритм получил развитие и стал основой нового, более безопасного шифра KHAZAD. Алгоритм Rijndael так же можно считать основанным на идеях шифра SHARK и его потомком.

Serpent

Разработан Россом Андерсоном, Эли Бихамом и Ларсом Кнудсеном. Некоторые предыдущие разработки авторов тоже носили названия в честь животных, например Tiger, Bear.
Алгоритм являлся одним из финалистов 2-го этапа конкурса AES. Как и другие алгоритмы, участвовавшие в конкурсе AES, Serpent имеет размер блока 128 бит и возможные длины ключа 128, 192 или 256 бит. Алгоритм представляет собой 32-раундовую SP-сеть, работающую с блоком из четырёх 32-битных слов. Serpent был разработан так, что все операции могут быть выполнены параллельно, используя 32 1-битных «потока».
При разработке Serpent использовался более консервативный подход к безопасности, нежели у других финалистов AES, проектировщики шифра считали, что 16 раундов достаточно, чтобы противостоять известным видам криптоанализа, но увеличили число раундов до 32, чтобы алгоритм мог лучше противостоять ещё неизвестным методам криптоанализа.
Став финалистом конкурса AES, алгоритм Serpent в результате голосования занял 2 место.
Шифр Serpent не запатентован и является общественным достоянием.
Алгоритм создавался под лозунгом «криптографический алгоритм 21 века» для участия в конкурсе AES. Не использовались новые, непроверенные и неиспытанные технологии при создании шифра, который в случае принятия был бы использован для защиты огромных массивов финансовых транзакций и правительственной информации. Основным требованием к участникам конкурса AES было то, что алгоритм-претендент должен быть быстрее, чем 3DES, и предоставлять как минимум такой же уровень безопасности: он должен иметь блок данных длиной 128 бит и ключ длиной 256 бит. 16-раундовый Serpent был бы таким же надежным, как 3DES, но в два раза быстрее. Однако, авторы посчитали, что для большей надежности стоит увеличить количество раундов до 32. Это сделало шифр таким же быстрым, как DES, и намного более надежным, чем 3DES.

Seal

Симметричный поточный алгоритм шифрования данных, оптимизированный для программной реализации.
Разработан в IBM Филом Рогэвеем (англ.) (англ. Phil Rogaway) и Доном Копперсмитом (англ. Don Coppersmith) в 1993 году. Алгоритм оптимизирован и рекомендован для 32-битных процессоров. Для работы ему требуется кэш-память на несколько килобайт и восемь 32-битовых регистров. Скорость шифрования — примерно 4 машинных такта на байт текста. Для кодирования и декодирования используется 160-битный ключ. Чтобы избежать нежелательной потери скорости по причине медленных операций обработки ключа, SEAL предварительно выполняет с ним несколько преобразований, получая в результате три таблицы определенного размера.
Непосредственно для шифрования и расшифрования текста вместо самого ключа используются эти таблицы.
Алгоритм считается очень надёжным, очень быстрым и защищён патентом США № 5454039 с декабря 1993 года.
В 1991 году Ральф Меркл (англ. Ralph C. Merkle) описал рентабельность программно-ориентированных шифров. По его мнению, наиболее эффективными из них были Khufu, FEAL и RC4. Однако постоянно увеличивающиеся потребности клиентов в надежной криптографии требовали поиска новых и доработки старых решений.
Летом 1992 года началась разработка первой версии нового программно-оптимизированного алгоритма SEAL 1.0. Разработчики взяли основные идеи и принцип работы из блочного шифра Ральфа Меркла (англ. Ralph C. Merkle) Khufu, который показался им самым совершенным на тот момент. Они решили добиться лучших характеристик проекта (в основном скорости), сузив круг аппаратуры, на которой возможна его реализация. Выбор был сделан в пользу 32-битных машин минимум с восемью регистрами общего назначения и кэшем не менее 8 Кбайт. В марте 1993 года было принято решение создать блочный шифр, но структура из семейства псевдослучайных функций, разработанная к октябрю того же года, работала быстрее, что склонило разработчиков в к поточному шифрованию. Эта структура состояла из четырех регистров, каждый из которых изменял своего «соседа» в зависимости от таблицы, полученной из ключа. После некоторого количества таких модификаций значения регистров добавляются в ключевую последовательность, которая растет с каждой итерацией до тех пор, пока не достигнет определенной длины. При разработке почти все внимание уделялось внутреннему циклу алгоритма, так как процедуру инициализации регистров и метод генерации таблиц из ключа оказывали незначительное влияние на его защищенность. В окончательном виде проект SEAL 1.0 появился только в декабре 1993 года.
В 1996 году Helena Handschuh (англ.) и Henri Gilbert (англ.) описали атаки на упрощенную версию SEAL 1.0 и на сам SEAL 1.0. Им потребовалось текстов, каждый длиной в четыре 32-битных слова, чтобы найти зависимость псевдослучайной функции от ключа. В результате, в следующих версиях алгоритма SEAL 3.0 и SEAL 2.0 были сделаны некоторые доработки и изменения. Например, в версии 1.0 каждая итерация с ключевой последовательностью завершалась модификацией только двух регистров, а в версии 3.0 — модифицировались все четыре. Еще SEAL 3.0 и SEAL 2.0 использовали для генерации таблиц алгоритм SHA-1 (англ. Secure Hash Algorithm-1) вместо первоначального SHA, что сделало их более устойчивыми к криптоанализу.

Safer

Семейство симметричных блочных криптоалгоритмов на основе подстановочно-перестановочной сети. Основной вклад в разработку алгоритмов внёс Джеймс Мэсси. Первый вариант шифра был создан и опубликован в 1993 году.
Существует несколько вариантов шифра, отличающихся друг от друга длиной ключа шифрования и размерами блоков исходного текста.
Первая разновидность алгоритма — SAFER K-64 была разработана Джэймсом Мэсси для калифорнийской корпорации «Cylinc» в 1993 году. Опубликованный в том же году, алгоритм имел блок и ключ шифрования длиной в 64 бита. Для него рекомендовалось использовать 6 раундов шифрования. Однако, из-за необходимости увеличить длину ключа до 128 бит (так как была обнаружена слабость в первоначальном варианте алгоритма), Мэсси разработал новый вариант шифра SAFER K-128, который был опубликован на следующий год после SAFER K-64. Новый алгоритм включал в себя расписание ключей, разработанное министерством внутренних дел Сингапура, и в дальнейшем использовался им для различных целей. Также для этого алгоритма рекомендовалось использовать 10 (максимум 12) раундов шифрования.
Спустя некоторое время в первых вариантах алгоритма выявились некоторые слабости, обнаруженные Ларсом Кнудсеном и Шоном Мёрфи. Это повлекло за собой создание новых версий алгоритма, названных SAFER SK-64 и SAFER SK-128, в которых расписание ключей было изменено в соответствии со схемой, предложенной Кнудсеном. Также был разработан вариант с длиной ключа, уменьшенной до 40 бит — SAFER SK-40. Сокращение «SK» в названии алгоритмов расшифровывается как «Strengthened Key schedule» (Усиленное расписание ключей). Для новых вариантов шифра предлагалось использовать не 6, а по крайней мере 8 (максимум 10) раундов шифрования.
Алгоритм SAFER+ был разработан в 1998 году калифорнийской корпорацией Cylinc совместно с Армянской академией наук для участия в конкурсе AES, на котором прошёл лишь первый отборочный тур. Данный шифр имеет входной блок длиной 128 бит и размер ключа 128, 192 или 256 бит.
Последней из созданных разновидностей алгоритма SAFER является SAFER++, разработанный Мэсси в 2000 году и ставший дальнейшим развитием алгоритма SAFER+. Алгоритм принял участие в европейском конкурсе алгоритмов NESSIE, где был представлен в двух вариантах: шифр с 64-битным блоком и 128-битным блоком. Он прошёл во вторую фазу конкурса, но не был выбран в набор рекомендуемых NESSIE криптографических примитивов. Эксперты сочли, что шифр слишком медленный на всех машинах, кроме 8-битных (таких как смарт-карты), а запас безопасности шифра слишком мал.
Алгоритмы SAFER не являются частной собственностью и не защищены авторскими правами, то есть могут быть использованы без каких-либо ограничений. Поскольку они целиком состоят из простых байтовых операций (за исключением поворота байтов при генерации ключей), эти алгоритмы могут быть реализованы процессорами с малой разрядностью.

MISTY1

Блочный алгоритм шифрования, созданный на основе «вложенных» сетей Фейстеля 1995 году криптологом Мицуру Мацуи (Mitsuru Matsui) совместно с группой специалистов для компании Mitsubishi Electric. MISTY — это аббревиатура Mitsubishi Improved Security Technology, а также инициалы создателей алгоритма: в разработке алгоритма также приняли участие Тэцуя Итикава (Tetsuya Ichikawa), Дзюн Соримати (Jun Sorimachi), Тосио Токита (Toshio Tokita) и Ацухиро Ямагиси (Atsuhiro Yamagishi). Алгоритм был разработан в 1995 году, однако прошел лицензирование и был опубликован уже в 1996 году.
MISTY1 — это сеть Фейстеля с изменчивым числом раундов (рекомендовано 8, но оно может быть любым, кратным 4). Алгоритм работает с 64-битными блоками и использует 128-битный ключ. Шифр стал победителем среди алгоритмов, шифрующих 64-битные блоки, на Европейском конкурсе NESSIE. В результате анализа алгоритма, проведённого в рамках этого конкурса и до него, эксперты сделали вывод, что никаких серьёзных уязвимостей данный алгоритм не имеет (они особо отметили, что именно структура алгоритма с вложенными сетями Фейстеля существенно затрудняет криптоанализ). Аналогичные исследования были проведены и в рамках проекта CRYPTREC по выбору криптоалгоритмов для электронного правительства Японии. Эксперты проекта весьма положительно оценили алгоритм MISTY1, сделав вывод, что у него высокий запас криптостойкости, алгоритм имеет высокую скорость шифрования и весьма эффективен для аппаратной реализации.
MISTY1 запатентованный алгоритм. Однако исконный владелец патента, Mitsubishi Electric, объявил, что будет выдавать лицензию на использование бесплатно.
MISTY1 был разработан на основе теории «подтверждённой безопасности» против дифференциального и линейного криптоанализа. Этот алгоритм был спроектирован, чтобы противостоять различным криптоатакам, известным на момент создания.
С момента публикации мисти было проведено много исследований, чтобы оценить его уровень безопасности. Некоторые результаты по исследованию мисти с меньшим количеством раундов представлены ниже.
Дифференциальный криптоанализ высокого порядка эффективно применяется к блочным шифрам с малой степенью. Мисти содержит 2 look-up таблицы S7 и S9, обе с малой ad, 3 и 2 соответственно. Поэтому достаточно много статей посвящены дифференциальному криптоанализу мисти. Наилучший результат был получен для 5-уровневого алгоритма без FL функций. Однако именно присутствие FL функций и широкобитных AND/OR операции в них сильно затрудняет использование дифференциального криптоанализа высокого порядка.
Невозможный дифференциальный анализ также применим к блочному шрифту с одинаковым значением подключа в каждом раунде (или в каждом n-ом раунде). И так как MISTY1 имеет достаточно простую систему расширения ключа, вполне естественно рассмотреть применимость данной атаки к данному алгоритму. Лучший результата для подобной атаки был также получен при рассмотрении алгоритма без FL функций.
Шифр стал победителем среди алгоритмов, шифрующих 64-битные блоки, на Европейском конкурсе NESSIE (2000—2003 года). В результате анализа алгоритма, проведённого в рамках этого конкурса и до него, эксперты сделали вывод, что никаких серьёзных уязвимостей данный алгоритм не имеет (они особо отметили, что именно структура алгоритма с вложенными сетями Фейстеля существенно затрудняет криптоанализ).
Аналогичные исследования были проведены и в рамках проекта CRYPTREC по выбору криптоалгоритмов для электронного правительства Японии. Эксперты проекта весьма положительно оценили алгоритм MISTY1, сделав вывод, что у него высокий запас криптостойкости, алгоритм имеет высокую скорость шифрования и весьма эффективен для аппаратной реализации.
Существует модификация данного алгоритма — MISTY2. Однако она не получила широкой известности вследствие низкого уровня криптостойкости.
Так же получила распространение модификация MISTY1 — алгоритм KASUMI — в 2000 году стал стандартом шифрования мобильной связи W-CDMA.
KASUMI (от японск.霞 (hiragana かすみ, romaji kasumi) — туман, mist) — блочный шифр, использующийся в сетях сотовой связи 3GPP. Также обозначается A5/3 при использовании в GSM и GEA3 в GPRS.
KASUMI разработан группой SAGE (Security Algorithms Group of Experts), которая является частью Европейского Института по Стандартизации в области Телекоммуникаций (ETSI). За основу был взят существующий алгоритм MISTY1 и оптимизирован для использования в сотовой связи.
Как показали в 2010 году криптоаналитики, в процессе изменений надежность алгоритма MISTY1 была снижена: KASUMI имеет уязвимости к некоторым типам атак, тогда как MISTY1 является стойким по отношению к ним.
KASUMI использует 64-битный размер блока и 128-битный ключ в 8-раундовой схеме Фейстеля. В каждом раунде используется 128-битный раундовый ключ, состоящий из восьми 16-битных подключей, полученных из исходного ключа по фиксированной процедуре генерации подключей.

Mars

Шифр-кандидат в AES, разработанный корпорацией IBM, создавшей в своё время DES. По заявлению IBM, в алгоритм MARS вложен 25-летний криптоаналитический опыт фирмы, и наряду с высокой криптографической стойкостью шифр допускает эффективную реализацию даже в таких ограниченных рамках, какие характерны для смарт-карт.
В разработке шифра принял участие Дон Копперсмит, один из авторов шифра Lucifer (DES), известный рядом статей по криптологии: улучшение структуры S-блоков против дифференциального криптоанализа, метод быстрого перемножения матриц (алгоритм Копперсмита — Винограда), криптоанализ RSA. Кроме него в разработке алгоритма приняли участие: Кэролин Барвик, Эдвард Д’Эвиньон, Росарио Женаро, Шай Халеви, Чаранжит Джутла, Стивен M. Матьяс Мл., Люк О'Коннор, Мохамед Перьевян, Дэвид Саффорд, Невенко Зунич.
По правилам конкурса AES, участники могли вносить незначительные изменения в свои алгоритмы. Воспользовавшись этим правилом, авторы MARSa изменили процедуру расширения ключа, что позволило снизить требования к энергонезависимой и оперативной памяти. Ниже будет предоставлена модифицированная версия алгоритма.
По результатам конкурса AES, MARS вышел в финал, но уступил Rijndael. После объявления результатов (19 Мая 2000 года) группа разработчиков составила своё собственное мнение о конкурсе AES, где дала комментарии на претензии к своему детищу.
Сейчас MARS распространяется по всему миру под лицензией Royalty-free. Алгоритм уникален тем, что использовал практически все существующие технологии, применяемые в криптоалгоритмах, а именно:

• простейшие операции (сложение, вычитание, исключающее или)
• подстановки с использованием таблицы замен
• фиксированный циклический сдвиг
• зависимый от данных циклический сдвиг
• умножение по модулю 232
• ключевое забеливание

Использование двойного перемешивания представляет сложность для криптоанализа, что некоторые относят к недостаткам алгоритма. В то же время на данный момент не существует каких-либо эффективных атак на алгоритм, хотя некоторые ключи могут генерировать слабые подключи.

Loki

В криптографии, LOKI89 и LOKI91 являются симметричным ключом блочных шифров, предназначенные в качестве возможной замены для стандарта DES (Data Encryption). Были разработаны шифры основаны на теле работы анализирующей DES, и очень похожи на DES в структуре. Алгоритмы Локи были названы по имени Локи, бога озорства в скандинавской мифологии
LOKI89 был впервые опубликован в 1990 году, тогда называли просто «LOKI», австралийскими криптографами Лори Браун, Джозеф Pieprzyk, и Дженнифер Seberry. LOKI89 был представлен Европейскому RIPE проекта для оценки, но не был выбран.
Шифр использует 64-битовый блок и 64-битовый ключ. Как и DES, это 16-круглый сеть фейстеля и имеет аналогичную общую структуру, но отличается от выбора конкретных S-боксов, «P-перестановки», а «Расширительный перестановка». S-коробки использовать критерии нелинейность, разработанные Josef Pieprzyk, делая их как «комплекс» и «unpredicatable», насколько это возможно. Их эффективность сравнивали с известными проектными критериями для DES S-боксов. Перестановки были разработаны, чтобы «смешивать» выходы S-боксов как можно быстрее, способствуя лавина и полноты свойств, необходимых для хорошего Feistel шифра. Однако в отличие от их эквивалентов в DES, они предназначены, чтобы быть чистым и простым, насколько это возможно (в ретроспективе, возможно, немного слишком просто), пособничество анализ конструкции.
После публикации LOKI89, информацию о новом дифференциального криптоанализа стали доступны, а также некоторые результаты раннего анализа путем (Кнудсена 1993a). Это привело к конструкции изменяется, чтобы стать LOKI91.
LOKI 91 был разработан в ответ на нападения на LOKI89 (Brown и др., 1991). Изменения включали удаление начального и конечного ключа Отбеливание, новый S-бокс, а также небольшие изменения в расписания ключей. Более конкретно, S-блоков были изменены, чтобы свести к минимуму вероятность того, видеть различные входы, приводящие к тем же выходом (крючок, который использует дифференциальный криптоанализ), тем самым улучшая иммунитет LOKI91 к этой атаке, как подробно описано авторами атаки (Biham и Шамира 1991). Изменения расписания ключей были разработаны, чтобы уменьшить число «эквивалентных» или «связанных с» ключами, которые привели к переборного пространства для шифра сокращается.
В то время как в результате шифра явно сильнее и безопаснее, чем LOKI89, существует целый ряд потенциальных атак, как подробно описано в работах Кнудсена и Biham. Следовательно, эти шифры следует рассматривать как научные усилия по продвижению в области разработки блочных шифров, а не алгоритмы для использования. Количество цитат и опубликованных критических замечаний свидетельствует эта цель была достигнута.

Idea

Симметричный блочный алгоритм шифрования данных, запатентованный швейцарской фирмой Ascom. Известен тем, что применялся в пакете программ шифрования PGP. В ноябре 2000 года IDEA был представлен в качестве кандидата в проекте NESSIE в рамках программы Европейской комиссии IST (англ. Information Societies Technology, информационные общественные технологии).
Первую версию алгоритма разработали в 1990 году Лай Сюэцзя (Xuejia Lai) и Джеймс Мэсси (James Massey) из Швейцарского института ETH Zürich (по контракту с Hasler Foundation, которая позже влилась в Ascom-Tech AG) в качестве замены DES (англ. Data Encryption Standard, стандарт шифрования данных) и назвали её PES (англ. Proposed Encryption Standard, предложенный стандарт шифрования). Затем, после публикации работ Бихама и Шамира по дифференциальному криптоанализу PES, алгоритм был улучшен с целью усиления криптостойкости и назван IPES (англ. Improved Proposed Encryption Standard, улучшенный предложенный стандарт шифрования). Через год его переименовали в IDEA (англ. International Data Encryption Algorythm).
Так как IDEA использует 128-битный ключ и 64-битный размер блока, открытый текст разбивается на блоки по 64 бит. Если такое разбиение невозможно, последний блок дополняется различными способами определённой последовательностью бит. Для избежания утечки информации о каждом отдельном блоке используются различные режимы шифрования. Каждый исходный незашифрованный 64-битный блок делится на четыре подблока по 16 бит каждый, так как все алгебраические операции, использующиеся в процессе шифрования, совершаются над 16-битными числами. Для шифрования и расшифрования IDEA использует один и тот же алгоритм.
Фундаментальным нововведением в алгоритме является использование операций из разных алгебраических групп, а именно:

• сложение по модулю
• умножение по модулю
• побитовое исключающее ИЛИ (XOR).

Эти три операции несовместимы в том смысле, что:

• никакие две из них не удовлетворяют дистрибутивному закону
• никакие две из них не удовлетворяют ассоциативному закону

Применение этих трех операций затрудняет криптоанализ IDEA по сравнению с DES, который основан исключительно на операции исключающее ИЛИ, а также позволяет отказаться от использования S-блоков и таблиц замены. IDEA является модификацией сети Фейстеля.

Phelix

Высокоскоростной поточный шифр, использующий одноразовый код аутентичности сообщения. Шифр был представлен на конкурсе eSTREAM в 2004 году. Авторами являются Брюс Шнайер, Дуг Уитинг, Стефан Люкс и Фредерик Мюллер. Алгоритм содержит операции сложения по модулю 232, сложения по модулю 2 и циклический сдвиг; Phelix использует 256-битный ключ и 128-битную метку времени метку времени (англ.). Некоторыми криптографами были выражены опасения насчет возможности получения секретного ключа при некорректном использовании шифра.
Предтечей к Phelix стал шифр Helix, построенный на простейших операциях, но он оказался взломан. Усовершенствованный Helix получил название Phelix, но и он был отвергнут на конкурсе eCrypt. Причина отказа была спорной-атаки основывались на подборе метки времени, что являлось слабым местом и других шифров, но разработчики заявили, что их шифр устойчив к данного рода атакам. Оказалось, что шифр взламывается дифференциально-линейным криптоанализом, хотя стойкости шифра в других условиях это не угрожает. В итоге Phelix не был допущен к третьему раунду конкурса, за некоторую самонадеянность и неаккуратность авторов. Помимо всего этого, появился ряд теоретических работ, в которых утверждалось, что смешение операций add-xor-shift не дает необходимой нелинейности, но на практике взломов не было. Теперь дизайн Phelix предлагается авторами к использованию в Skein и Threefish.
Авторы сообщают, что Phelix не должен использоваться, пока он не получил дополнительного криптоанализа.
Хунцзюнь Ву и Барт Пренил, авторы дифференциальной атаки, выражают беспокойчтво тем, что каждое слово открытого текста влияет на ключевой поток, минуя достаточные конфузионные и диффузионные слоя. Они утверждают, что это свойственный недостаток в структуре Helix и Phelix. Авторы приходят к выводу, что Phelix небезопасен.

Feal

Блочный шифр, разработанный Акихиро Симидзу (англ. Akihiro Shimizu) и Сёдзи Миягути (англ. Shoji Miyaguchi) — сотрудниками компании NTT.
В нём используются 64-битовый блок и 64-битовый ключ. Его идея состоит и в том, чтобы создать алгоритм, подобный DES, но с более сильной функцией этапа. Используя меньше этапов, этот алгоритм мог бы работать быстрее. К тому же, в отличие от DES, функция этапа для FEAL не использует S-блоки, поэтому реализация алгоритма не требует дополнительной памяти для хранения таблиц замены.
Опубликованный в 1987 году Акихиро Симидзу и Сёдзи Миягути блочный шифр FEAL был разработан с целью повысить скорость шифрования без ухудшения надежности шифра, по сравнению с DES. Первоначально алгоритм использовал блоки размером 64 бита, ключ размером 64 бита и 4 раунда шифрования. Однако, уже в 1988 году была опубликована работа Берта ден Боера (англ. Bert Den-Boer), доказывающая достаточность владения 10000 шифротекстов для проведения успешной атаки на основе подобранного открытого текста. К шифру FEAL одному из первых был применен линейный криптоанализ. В том числе в 1992 году Митсуру Мацуи и Ацухиро Ямагиси доказали, что достаточно узнать 5 шифротекстов для проведения успешной атаки.
Для борьбы с обнаруженными уязвимостями создатели удвоили число раундов шифрования, опубликовав стандарт FEAL-8. Однако, уже в 1990 году Генри Гилберт (англ. Henri Gilbert) уязвимость и этого шифра перед атакой на основе подобранного открытого текста. Далее в 1992 году Митсуру Матсуи и Ацухиро Ямагиси (Mitsuru Matsui and Atsuhiro Yamagishi) описали атаку на основе открытых текстов.
В связи с большим числом успешных атак, разработчиками было принято решение еще усложнить шифр. А именно, в 1990 году был представлен FEAL-N, где N — произвольное четное число раундов шифрования, и представлен FEAL-NX, где X (от англ. extended) обозначает использование расширенного до 128 бит ключа шифрования. Однако данное нововведение помогло лишь частично. В 1991 году Эли Бихам и Ади Шамир (Eli Biham and Adi Shamir), используя методы дифференциального криптоанализа, показали возможность взлома шифра быстрее, чем полным перебором.
Тем не менее, благодаря интенсивности исследования алгоритма шифрования сообществом, были доказаны границы уязвимости шифра перед линейным и дифференциальным криптоанализом. Устойчивость алгоритма с числом раундов большим 26 к линейному криптоанализу показали в своей работе Шихо Мораи, Казумаро Аоки и Казуо Охта (Shiho Moriai, Kazumaro Aoki, and Kazuo Ohta), а в работе Казумаро Аоки, Кунио Кобаяси и Шихо Мораи (Kazumaro Aoki, Kunio Kobayashi, and Shiho Moriai) была доказана невозможность применить дифференциальный криптоанализ к алгоритму, использующему больше 32 раундов шифрования.
Благодаря тому, что шифр FEAL был разработан достаточно рано, он послужил отличным объектом для тренировок для криптологов всего мира.
Кроме того, на его примере были открыт линейный криптоанализ. Мицуру Мацуи, изобретатель линейного криптоанализа, в первой своей работе на эту тему рассматривал как раз FEAL и DES.

Двухключевые КА

RSA

RSA — аббревиатура от фамилий Rivest, Shamir и Adleman криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. Описан в 1977 году Рон Ривест, Ади Шамир и Леонард Адлеман из Массачусетского технологического института
Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи. Алгоритм используется в большом числе криптографических приложений, включая PGP, S/MIME, TLS/SSL, IPSEC/IKE и других. Алгоритм Rivest-Shamir-Adleman (RSA) является одним из самых популярных и безопасных методов шифрования с открытым ключом. Алгоритм основывается на том, что нет эффективного способа учета очень больших (100-200 цифр) чисел.

RSA-ключи генерируются следующим образом:

1. Выбираются два различных случайных простых числа и заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение , которое называется модулем.
3. Вычисляется значение функции Эйлера от числа:
   
4. Выбирается целое число ( ), взаимно простое со значением функции φ(n) . Обычно в качестве берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
   • Число называется открытой экспонентой (англ. public exponent)
   • Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в .
   • Слишком малые значения , например 3, потенциально могут ослабить безопасность схемы RSA.

5. Вычисляется число , мультипликативно обратное к числу по модулю , то есть число, удовлетворяющее сравнению:
   Число называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
6. Пара {} публикуется в качестве открытого ключа RSA.
7. Пара {} играет роль закрытого ключа RSA и держится в секрете.

Безопасность RSA зависит от вычислительной сложности факторизации больших целых чисел. По мере увеличения вычислительной мощности и выявления более эффективных алгоритмов факторинга увеличивается и способность к увеличению числа и больших чисел. Шифрование напрямую привязана к размеру ключа, а удвоение длины ключа обеспечивает экспоненциальное увеличение прочности, хотя и снижает производительность.

DSA

DSA — криптографический алгоритм с использованием открытого ключа для создания электронной подписи, но не для шифрования (в отличие от RSA и схемы Эль-Гамаля). Подпись создается секретно, но может быть публично проверена. Это означает, что только один субъект может создать подпись сообщения, но любой может проверить её корректность. Алгоритм основан на вычислительной сложности взятия логарифмов в конечных полях.
Алгоритм был предложен Национальным институтом стандартов и технологий (США) в августе 1991 и является запатентованным, НИСТ сделал этот патент доступным для использования без лицензионных отчислений. DSA является частью DSS, впервые опубликованного 15 декабря 1998. Стандарт несколько раз обновлялся, последняя версия FIPS-186-4.
DSA включает в себя два алгоритма (S, V): для создания подписи сообщения (S) и для ее проверки (V).
Оба алгоритма вначале вычисляют хэш сообщения, используя криптографическую хэш-функцию. Алгоритм S использует хэш и секретный ключ для создания подписи, алгоритм V использует хэш сообщения, подпись и открытый ключ для проверки подписи.
Фактически подписывается не сообщение (произвольной длины), а его хеш (160-256 бит).

Подпись сообщения выполняется по следующему алгоритму:

1. Выбор случайного числа
2. Вычисление
3. Вычисление
4. Выбор другого , если оказалось, что или
5. Подписью является пара чисел

Проверка подписи

Проверка подписи выполняется по алгоритму:

1. Вычисление
2. Вычисление
3. Вычисление
4. Вычисление
5. Подпись верна, если

#include < CkCrypt2 .h>
 #include < CkDsa .h>

void ChilkatSample ( void )
    {
    bool успех;

    // Используйте Chilkat Crypt для хеширования содержимого файла. 
    // Это разблокирует объекты crypt и DSA. 
    CryptCrypt2 crypt;
    success = crypt. UnlockComponent ( «Все для 30-дневной пробной версии » );
    if (success! = true ) {
         std :: cout << crypt. lastErrorText () << " r  n";
        возвращение ;
    }

    крипты. put_EncodingMode ( "hex" );
    крипты. put_HashAlgorithm ( "sha-1" );

    // Возвращает хэш SHA-1 файла. Файл может быть любого размера. 
    // Компонент Chilkat Crypt будет передавать файл, когда 
    // вычисляет хэш, сохраняя постоянство использования памяти 
    // и разумным. 
    // 20-байтовый SHA-1 хэш возвращается в виде строки с шестнадцатеричным кодированием. 
    const char * hashStr = crypt. hashFileENC ( "hamlet.xml" );

    CkDsa dsa;

    // Загрузите закрытый ключ DSA из файла PEM. Chilkat DSA 
    // предоставляет возможность загружать и сохранять общедоступные и частные 
    ключи 
    DSA из зашифрованных или незашифрованных PEM или DER. // Метод LoadText предназначен только для удобства. Вы можете 
    // использовать любые средства для загрузки содержимого файла PEM в 
    // строку. 
    const char * pemPrivateKey = 0;
    pemPrivateKey = dsa. loadText ( "dsa_priv.pem" );
    success = dsa. FromPem (pemPrivateKey);
    if (success! = true ) {
         std :: cout << dsa. lastErrorText () << " r  n";
        возвращение ;
    }

    // Вы можете дополнительно проверить ключ, чтобы убедиться, что он является допустимым 
    // DSA-ключом. 
    success = dsa. VerifyKey ();
    if (success! = true ) {
         std :: cout << dsa. lastErrorText () << " r  n";
        возвращение ;
    }

    // Загрузим хэш для входа в объект DSA: 
    success = dsa. SetEncodedHash ( "hex" , hashStr);
    if (success! = true ) {
         std :: cout << dsa. lastErrorText () << " r  n";
        возвращение ;
    }

    // Теперь, когда объект DSA содержит как закрытый ключ, так и хэш, 
    // он готов к созданию подписи: 
    success = dsa. SignHash ();
    if (success! = true ) {
         std :: cout << dsa. lastErrorText () << " r  n";
        возвращение ;
    }

    // Если SignHash успешно, объект DSA содержит 
    подпись //. Он может быть доступен как 
    строка 
    с шестнадцатеричным или base64-кодированием . (Также можно получить доступ непосредственно в форме массива байтов через // свойство «Подпись».)
     Const char * hexSig = dsa. getEncodedSignature ( "hex" );
    std :: cout << "Подпись:" << " r  n";
    std :: cout << hexSig << " r  n";

    // ------------------------------------------------ ----------- 
    // Шаг 2. Проверка подписи DSA 
    // ---------------------------- -------------------------------

    CkDsa dsa2;

    // Загрузите открытый ключ DSA для проверки: 
    const char * pemPublicKey = 0;
    pemPublicKey = dsa2. loadText ( "dsa_pub.pem" );
    success = dsa2. FromPublicPem (pemPublicKey);
    if (success! = true ) {
         std :: cout << dsa2. lastErrorText () << " r  n";
        возвращение ;
    }

    // Загрузим хэш для проверки подписи. 
    success = dsa2. SetEncodedHash ( "hex" , hashStr);
    if (success! = true ) {
         std :: cout << dsa2. lastErrorText () << " r  n";
        возвращение ;
    }

    // Загружаем подпись: 
    success = dsa2. SetEncodedSignature ( "hex" , hexSig);
    if (success! = true ) {
         std :: cout << dsa2. lastErrorText () << " r  n";
        возвращение ;
    }

    // Verify: 
    success = dsa2. Verify ();
    if (success! = true ) {
         std :: cout << dsa2. lastErrorText () << " r  n";
    }
    else {
         std :: cout << «Подпись подтверждена DSA!» << " r  n";
    }


    }

Elgamal

Асимметричный алгоритм, предложенный в 1985 году Эль-Гамалем (T. ElGamal), универсален. Он может быть использован для решения всех трех основных задач: для шифрования данных, для формирования цифровой подписи и для согласования общего ключа. Кроме того, возможны модификации алгоритма для схем проверки пароля, доказательства идентичности сообщения и другие варианты. Безопасность этого алгоритма, так же как и алгоритма Диффи-Хеллмана, основана на трудности вычисления дискретных логарифмов. Этот алгоритм фактически использует схему Диффи-Хеллмана, чтобы сформировать общий секретный ключ для абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ.
И в случае шифрования, и в случае формирования цифровой подписи каждому пользователю необходимо сгенерировать пару ключей. Для этого, так же как и в схеме Диффи-Хеллмана, выбираются некоторое большое простое число и число , такие, что различные степени А представляют собой различные числа по модулю . Числа Р и А могут передаваться в открытом виде и быть общими для всех абонентов сети.
Затем каждый абонент группы выбирает свое секретное число , и вычисляет соответствующее ему открытое число. Таким образом, каждый пользователь может сгенерировать закрытый ключ и открытый ключ .

Rabin

Этот алгоритм был опубликован в январе 1979 года Майклом О. Рабином. Криптосистема Рабина была первой асимметричной криптосистемой, в которой восстановление всего открытого текста из зашифрованного текста можно было доказать так же сильно, как факторинг.

Генерация ключа:

Выберем два больших разных числа p и q. Можно выбратьдля упрощения вычисления квадратных корней по модулю p и q (см. ниже). Но схема работает с любыми штрихами.
Позволять , Тогда n является открытым ключом. Простые числа и являются закрытым ключом.
Для шифрования сообщения необходим только открытый ключ . Чтобы расшифровать зашифрованный текст, необходимы факторы и , .

Генерация ключа

1. выбираются два случайных числа p и q с учётом следующих требований:
2. числа должны быть большими (см. разрядность);
3. числа должны быть простыми;
4. должно выполняться условие:.

Выполнение этих требований сильно ускоряет процедуру извлечения корней по модулю р и q;
вычисляется число ;

1. число n — открытый ключ;
2. числа p и q — закрытый.

Шифрование

Исходное сообщение m (текст) шифруется с помощью открытого ключа — числа n по следующей формуле:
Благодаря использованию умножения по модулю скорость шифрования системы Рабина больше, чем скорость шифрования по методу RSA, даже если в последнем случае выбрать небольшое значение экспоненты.

Расшифровка
Для расшифровки сообщения необходим закрытый ключ — числа p и q. Процесс расшифровки выглядит следующим образом:

1. Сначала, используя алгоритм Евклида, из уравнения находят числа и ;
2. далее, используя китайскую теорему об остатках, вычисляют четыре числа:

   

Одно из этих чисел является истинным открытым текстом m.

P.S. Если кому интересно, то почти по всем алгоритмам, представленным в данной статье, имеются архивы, с реализацией на С, С++ или Ассемблере(на каком-то из языков), соответственно реализации не мои, скажу больше использовать их навряд ли получится, хотя кто знает.
P.P.S. Была идея также сделать Сравнительную таблицу, но для начала хотелось бы узнать, по каким именно параметрам Вы хотели бы увидеть сравнение.

Автор: den_golub

Источник