Вступление
- Моделирование транспортных потоков стало одной из лидирующих проблем в науке, чуть ли не с появления первых автомобилей. Считается, что родоначальником данной отрасли является учёный ещё из царской России Дубелир со своей книгой «Городские улицы и мостовые» (1912 год). За 100 лет непрерывных исследований выработалось много хороших моделей, которые помогают сегодня строить качественные и быстрые дороги. Но если Вы думаете, что не осталось нерешённых вопросов, Вы сильно ошибаетесь, ведь до сих пор светлые умы нашей планеты ломают головы над решениями задач, о которых иногда спрашивают даже дети. Например, как настроить светофор так, чтобы около него не образовывалась пробка?
Кратчайший путь
- Как можно было догадаться, дорожную сеть обычно представляют в виде графа.
Несмотря на то, что большинство дорог двусторонние, существуют и односторонние участки, значит граф ориентированный.Для облегчения понимания, будем считать, что граф связанный, а именно, что из любой вершины графа всегда можно попасть в любую другую.
Представим такую ситуацию, из города А в город Б ведёт две пустые дороги с одинаковым покрытием, какую выбрать лучше? Правильный ответ: которая короче.
Значит граф взвешенный, так как каждому ребру можно поставить в соответствие число, например, являющееся длиной соответственной дороги. Такая система будет выглядеть примерно вот так…

- Но если бы всё было так просто, компании не тратили бы огромные суммы на разработку продвинутых навигаторов. А всё из-за того, что бывают высокоскоростные магистрали, а бывают сельские грунтовки, бывают узкие городские улочки, а бывает мкад. Ну и соответственно главная проблема выбора правильной трассы — это пробки.
Вместо того, чтобы над рёбрами писать кучу характеристик, обычно пишут функцию, а именно зависимость времени прохождения участка дороги от количества автомобилей.
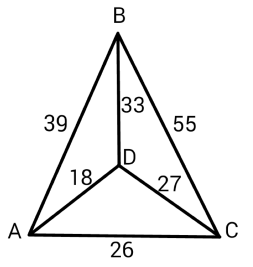
На данной схеме
— это количество машин, проезжающих через выбранное поперечное сечение за единицу времени на промежутке между городами 1-2
Максимальный Поток
- А теперь, давайте переключимся на роль генплана какого-нибудь города. Вы хотите узнать насколько хороша Ваша дорожная сеть. Чаще всего нужно выяснить сколько машин могут одновременно ехать по той или иной трассе. Во времена второй мировой войны ВВС США очень интересовало, насколько быстро и какое количество военных можно перенаправить в критические точки боевых действий. Решение проблемы нашёл Математик Джордж Бернард Данциг.
Пусть ёмкость ребра — это максимальная интенсивность потока, проходящая через ребро.
А насыщенное ребро — это ребро, по которому проходит максимальный поток.
Присвоим каждому участку пару чисел (,
).
— достигнутый до сих пор поток по ребру, вначале он равен нулю, затем это число будет только увеличиваться, пока не достигнет
, ёмкости ребра.
Пока хотя бы на одном маршруте извсе рёбра — ненасыщенные (то есть на всех рёбрах
<
), цикл продолжается.
1. Ищем любой участок трассы, содержащий только ненасыщенные рёбра изв
. Если подобный участок мы найти не можем, то цикл прекращается, максимальный поток, который мы пытаемся найти — это сумма потоков рёбер, приходящих в
.
2. Мы нашли дополняющий маршрут. Определяем значение максимального потока, который мы можем пропустить по данному маршруту. Он определяется как минимальная из всех возможных разностей ёмкости
и существующего потока c по всем рёбрам маршрута.
3. Каждоена ребре складываем с
, таким образом хотя бы одно ребро преобразуется в насыщенное.
4. Возвращаемся к (1.)
Микроскопическая Модель
- В первых двух абзацах описывалась макроскопическая модель, однако ещё с 1950-х годов учёными начала рассматриваться микроскопическая модель. Основное отличие заключается в том, что поток рассматривается не как единое целое, а как каждый автомобиль по отдельности.
- В микроскопических моделях транспортных потоков полагается, что ускорение конкретного автомобиля зависит от соседних транспортных средств. Наибольшее влияние на поведения водителя оказывает машина, движущееся впереди (лидер).
- Данная модель является сложной и неоднозначной, поэтому учёные до сих пор пишут статьи, в которых предлагают всё более совершенные функции, описывающие движение машин, однако чем более формула совершенна, тем более она становится больше и сложнее
Предпочтения Пассажира
- Представьте, что Вы — владеете крупным таксопарком и Вы пытаетесь понять, сколько оптимально иметь автомобилей, какую иметь политику приёма заказов и кого именно послать по звонку?
- Самый простой алгоритм перераспределения — ничего не делать, а когда на остановку придёт потенциальный клиент, послать к нему ближайший свободный автомобиль. Но вдруг у нас как раз к этому месту уже приближается автомобиль с пассажиром, которому нужно там выйти? Значит, мы отправили таксиста зря. Следовательно, надо учитывать и автомобили, которые уже направляются к нашей станции.
- Следующий важный вопрос — как построить так называемый эвристический алгоритм? Эвристическим называется алгоритм, который как-то использует некоторые вероятности из будущего. Например, мы знаем, что скоро прибудет поезд на станцию и из него выйдет много пассажиров, которые захотят взять такси. Может, стоит отправить туда автомобили заранее? Если да, то насколько заранее и сколько автомобилей?
Один из алгоритмов, для каждой станции задаёт некоторый индекс, зависящий от уже стоящих пассажиров, от некоторой статистики по будущим прибытиям и от местонахождения автомобилей в системе.
Перекрёстки
- Пусть нам задан перекрёсток следующего вида:
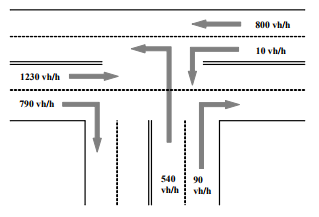
На рисунках указаны скорости потока в час пик и схема работы перекрёстка.
Какая длительность фаз светофора оптимальная (чтобы количество машин на перекрёстке было минимальным)? - Думаю, многие замечали, что большинство перекрёстков никак не используют информацию о потоках автомобилей и заданные на них длительности фаз светофора близки к рандомному. Многие предложат сделать длительности фаз пропорциональными потоку по каждому направлению. Но это может привести к тому, что будет скапливаться длинная пробка по одному из направлений. Эффективное решение, достаточно очевидно…
- Пусть поток автомобилей, двигающийся по шестиполосной дороге, доходит до T-образного перекрестка. И пусть целью трети водителей является поворот налево, а целью остальных — продолжить движение. Поворачивать и двигаться прямо одновременно нельзя (см.рисунок). В таком случае две левые полосы займут водители, которые хотят повернуть налево. Почему именно две полосы займут водители ответит сложная математическая модель. Поток транспортных средств через светофор при включении зелёного сигнала для прямого движения будет не теоретическим, максимально возможным для заданного числа полос (6000 автомобилей/час), а только 4 000 автомобилей/час. Значит на данном участке нужно не 6 полос, а всего лишь 4.
Автор: Alex_Microsoft