 Здравствуйте, коллеги. В конце 1960-ых годов прошлого века Ричард Фейнман прочитал в Калтехе курс лекций по общей физике. Фейнман согласился прочитать свой курс ровно один раз. Университет понимал, что лекции станут историческим событием, взялся записывать все лекции и фотографировать все рисунки, которые Фейнман делал на доске. Может быть, именно после этого у университета осталась привычка фотографировать все доски, к которым прикасалась его рука. Фотография справа сделана в год смерти Фейнмана. В верхнем левом углу написано: "What I cannot create, I do not understand". Это говорили себе не только физики, но и биологи. В 2011 году, Крейгом Венером был создан первый в мире синтетический живой организм, т.е. ДНК этого организма создана человеком. Организм не очень большой, всего из одной клетки. Помимо всего того, что необходимо для воспроизводства программы жизнедеятельности, в ДНК были закодированы имена создателей, их электропочты, и цитата Ричарда Фейнмана (пусть и с ошибкой, ее кстати позже исправили). Хотите узнать, к чему эта прохладная тут? Приглашаю под кат, коллеги.
Здравствуйте, коллеги. В конце 1960-ых годов прошлого века Ричард Фейнман прочитал в Калтехе курс лекций по общей физике. Фейнман согласился прочитать свой курс ровно один раз. Университет понимал, что лекции станут историческим событием, взялся записывать все лекции и фотографировать все рисунки, которые Фейнман делал на доске. Может быть, именно после этого у университета осталась привычка фотографировать все доски, к которым прикасалась его рука. Фотография справа сделана в год смерти Фейнмана. В верхнем левом углу написано: "What I cannot create, I do not understand". Это говорили себе не только физики, но и биологи. В 2011 году, Крейгом Венером был создан первый в мире синтетический живой организм, т.е. ДНК этого организма создана человеком. Организм не очень большой, всего из одной клетки. Помимо всего того, что необходимо для воспроизводства программы жизнедеятельности, в ДНК были закодированы имена создателей, их электропочты, и цитата Ричарда Фейнмана (пусть и с ошибкой, ее кстати позже исправили). Хотите узнать, к чему эта прохладная тут? Приглашаю под кат, коллеги.
Введение
На протяжении веков люди пытаются создать вещи, принцип работы которых не могут объяснить. Первой настоящей моделью искусственного интеллекта, совсем не мифического, и вполне понятно как работающего, стал персептрон Розенблатта. А потом все закрутилось. Рассмотрим область компьютерного зрения подробнее. Сегодня нейронные сети умеют отлично решать задачи классификации, сегментации и т.д., но как они это делают? Какие признаки выучивает сеть и являются ли они осмысленными — эти вопросы можно считать уже почти решенным. Вот пример того, как результаты этих работ позволяют нам сегодня манипулировать изображением. Но ведь манипулировать — это же не создавать, верно? Все еще есть проблемы, например, в данной работе вы можете увидеть, как добавление шума к изображению заставляет топовую нейросеть ошибаться, хотя невооруженный глаз изменений не видит. Вот если бы мы могли создавать изображения, тогда бы, возможно, мы смогли поставить точку в вопросе о понимании того, что на самом деле выучивает нейронная сеть и почему именно это, а не другое. Это, помните, как в Интерстелларе — последний рубеж в понимании гравитационной сингулярности находится в самой сингулярности. Вопрос об алгоритмической генерации фотореалистичных изображений не новый, но только в эпоху глубокого обучения удалось достигнуть существенных результатов. Сегодня мы с вами поговорим об одном из таких подходов, который стал одним из главных достижений последних лет в глубоком обучении. Оригинальная статья называется Generative Adversarial Nets (GAN) и пока нет устоявшегося перевода, мы будем называть их ГАНами. Как мне кажется, варианты "генеративные соревновательные сети" (ГСС) или "порождающие соперничающие сети" (ПСС), как-то не звучат.
Для начала разберем таксономию генеративных моделей, основанных на максимизации правдоподобия данных (включая те, которые делают это неявно; существуют и другие подходы к генерации данных, но они не пересекаются с ГАНами).
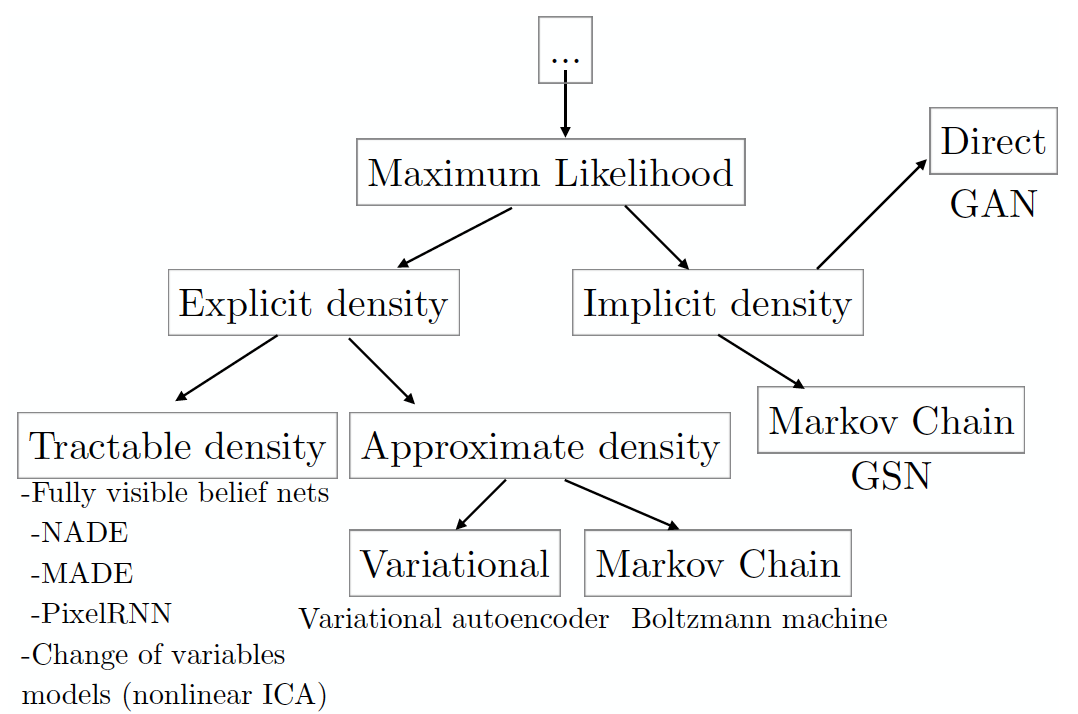
(изображение взято из статьи автора ГАНов, которая скомпилирована на основе его семинара на конференции NIPS 2016 года; оттуда же и вольный пересказ в нескольких абзацев ниже).
Вспомним, что суть принципа максимума правдоподобия заключается в поиске таких параметров модели, которые максимизируют правдоподобие набора данных, состоящего из 

Максимизация правдоподобия — это то же самое, что и минимизация KL-дивергенции между настоящим распределением данных и модельным:
Каждый лист дерева таксономии соответствует конкретной модели, которая обладает рядом плюсов и минусов. ГАНы были разработаны с целью нивелировать недостатки других моделей, что, естественно, привело к появлению новых недостатков. Но обо всем по порядку. В левом поддереве находятся модели с явно заданной формой функции плотности данных 

Если же модель создаёт изображения посредственного качества, или вы состарились, пока она обучалась, то, возможно, модели, аппроксимирующие плотность, решат проблему (см. лист approximate density). Таким моделям всё ещё необходимо предоставить явно выраженную формулу плотности распределения. Методы, основанные на вариационной аппроксимации (variational), максимизируют нижнюю оценку правдоподобия 
Главным недостатком таких моделей является то, что зазор между нижней оценкой 



От отчаяния вы можете решить использовать модели с неявно заданной функцией плотности (Implicit density) — модели, которые напрямую не формулируют 
- не требуют явно выраженной плотности, хотя можно сделать так, чтобы выучивалась нужная форма распределения (в этом смысле вариационные методы и ГАНы имеют связь);
- не требуется вывод нижней оценки логарифма правдоподобия;
- не нужно семплировать (точнее, семплирование есть, но только в один шаг, а не цепью);
- было замечено, что изображения получаются лучше, чем у других моделей (субъективная оценка, конечно);
- от себя добавлю, что эта модель одна из самых простых для понимания во всей вышеописанной категоризации.
Естественно, всё не так радужно, и в последующих частях разбора ГАНов мы узнаем о всех тех новых проблемах, которые появились вместе с новой моделью. Начнем с самой первой статьи, в которой ГАНы и были представлены для широкой публики.
Generative Adversarial Networks (10 Jun 2014)
Представим сюжет из фильма про противостояние фальшивомонетчика и полиции: один подделывает, другой ловит, ну вы поняли. Что получится, если мы заменим и того и другого нейронной сетью? Получится ролевая игра, пока только из двух актеров.  Generator – аналог фальшивомонетчика, сеть, которая генерирует данные (например, изображения), её задача уметь выдавать изображения, наиболее приближенные к целевой генеральной совокупности. Discriminator — аналог полицейского, точнее, того сотрудника аналитического отдела полиции по борьбе с фальшивомонетчиками; его задача — отличить оригинал монеты от подделки. Таким образом, дискриминатор – это не что иное как бинарный классификатор, который должен выдавать 1 для реальных изображений, и 0 для поддельных. Тут стоит вспомнить китайскую комнату: а что, если оптимальный дискриминатор не может отличить подделку от реальных, можем ли мы считать, что генератор стал генерировать реальные изображения, или это все еще подделка высокого качества? В целом модель выглядит следующим образом и обучается end-to-end методом обратного распространения ошибки:
Generator – аналог фальшивомонетчика, сеть, которая генерирует данные (например, изображения), её задача уметь выдавать изображения, наиболее приближенные к целевой генеральной совокупности. Discriminator — аналог полицейского, точнее, того сотрудника аналитического отдела полиции по борьбе с фальшивомонетчиками; его задача — отличить оригинал монеты от подделки. Таким образом, дискриминатор – это не что иное как бинарный классификатор, который должен выдавать 1 для реальных изображений, и 0 для поддельных. Тут стоит вспомнить китайскую комнату: а что, если оптимальный дискриминатор не может отличить подделку от реальных, можем ли мы считать, что генератор стал генерировать реальные изображения, или это все еще подделка высокого качества? В целом модель выглядит следующим образом и обучается end-to-end методом обратного распространения ошибки:
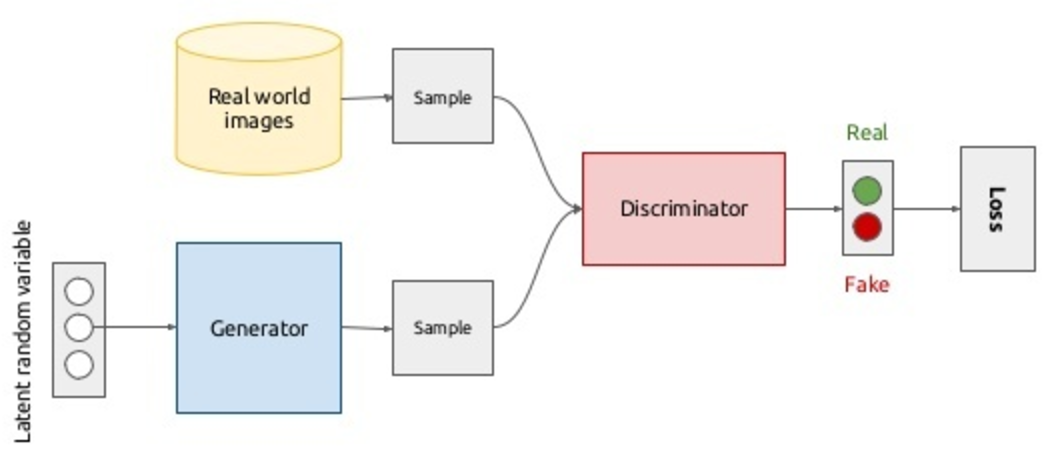
В принципе со сценарием в верхней половине диаграммы всё ясно: семплируем изображения из базы данных реальных изображений (
![Нейросетевая игра в имитацию - 18 $max_{D} mathbb{E}_{x sim p_{text{data}}}left[ log Dleft(xright) right] + mathbb{E}_{x sim p_{g}}left[ log left(1 - D(x)right) right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-18.svg)
![Нейросетевая игра в имитацию - 19 $Dleft(x, theta_dright) in left[0, 1right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-19.svg)






![Нейросетевая игра в имитацию - 26 $min_G mathbb{E}_{z sim p_zleft(zright)} left[ 1 - Dleft(Gleft(zright)right) right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-26.svg)

Вы можете заметить, что это очень похоже на начальные условия обучения с подкреплением, и будете правы. Каналом передачи информации от генератора дискриминатору является прямой проход по сети, а обратный проход — это способ передачи информации от дискриминатора к генератору. Возникает идея тренировать всю модель end-to-end, просто инвертируя градиенты, которые идут от дискриминатора, что позволит дискриминатору карабкаться выше по своей поверхности, а генератору спускаться по своей (см. следующую часть, где авторы вводят gradient reversal layer). Но именно для ГАНов такой подход не работает. В самом начале обучения дискриминатору очень легко отличить подделку от реальных данных (см. пример ниже). Тогда для фейковых данных 



Сравните какие семплы выдает сеть вначале обучения и на более поздней стадии.


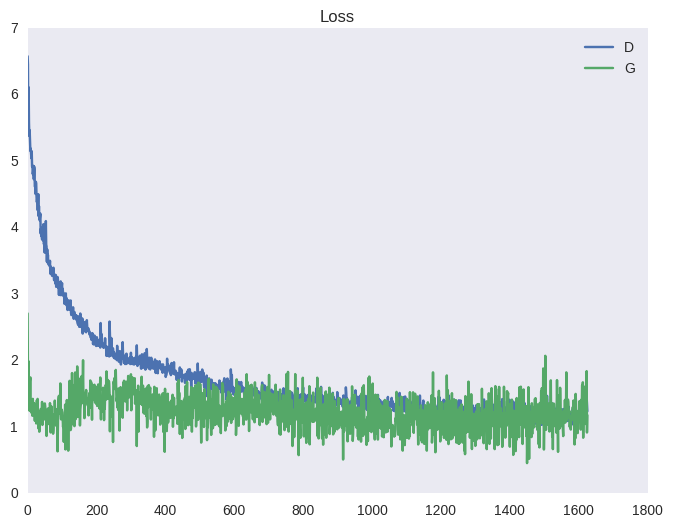
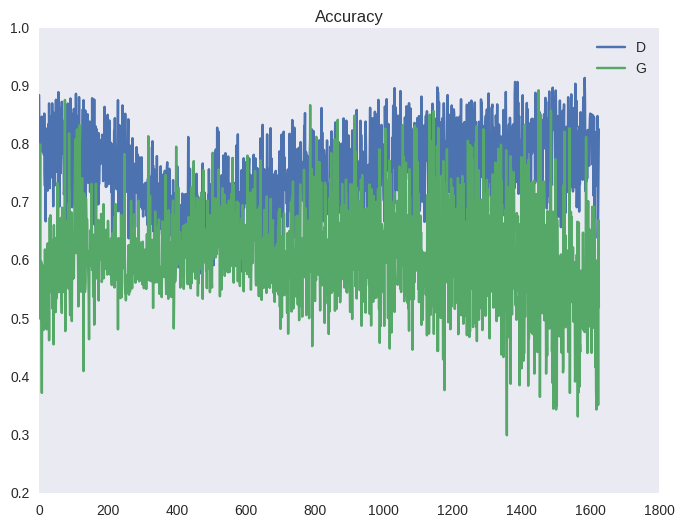
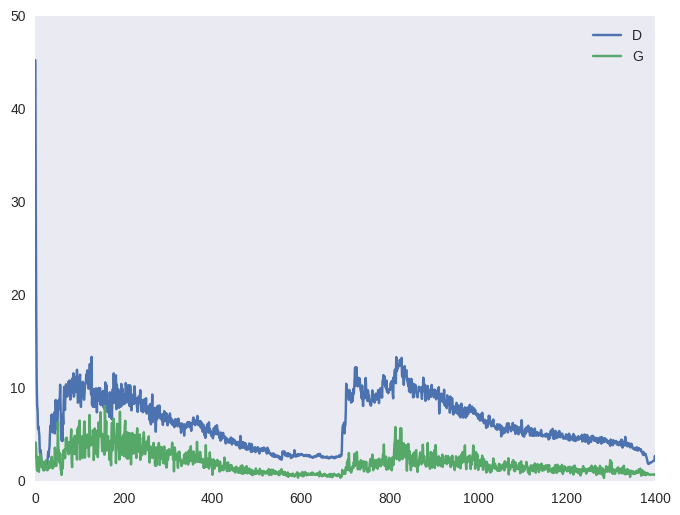
Чтобы гарантировать, что дискриминатор всегда будет около оптимума, авторы статьи предлагают следующий трюк. На каждой итерации обучения сначала несколько шагов обучается дискриминатор на батчах из реальных и поддельных изображений при фиксированном генераторе; затем делается один шаг обучения генератора на батче из поддельных изображений при фиксированном дискриминаторе. Это позволит держать дискриминатор всегда около оптимума и медленно менять генератор. В итоге получается игра в перетягивание каната, что выливается в нестабильное обучение. Ниже — типичная картина для функции стоимости ГАНа и для точности (среднее между количеством примеров, которые дискриминатор распознает верно в свою фазу обучения и в фазу обучения генератора). Эффект такого перетягивания вы можете наблюдать на графиках ниже, а также в виде ряби в примерах выше (под спойлером).
 |
 |
Давайте оценим, какие теоретические обоснования лежат в основе ГАНов. Во-первых, авторы доказывают, что для фиксированного генератора оптимальный дискриминатор имеет вид:
А дальше доказывают теорему о существовании глобального минимума функционала от функции генератора в точке 

В завершение обзора главной статьи, рассмотрим идеализированную визуализацию процесса сходимости и то, к чему он приводит:
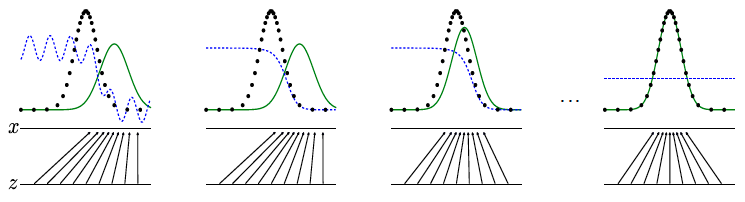
- линяя из черных точек — это распределение данных
, которое мы хотим приблизить нейросетью;
- зеленая линия — это распределение генератора
, в процессе обучения оно приближается к распределению данных (обучение происходит последовательно);
- синяя линия — это разделяющая поверхность дискриминатора, который в конце обучения не может отличить примеры из реального набора данных от подделки, созданной генератором;
- стрелками показано отображение
, которое ставит в соответствие каждому значению из распределения данных точку из априорного распределения.

Авторы приводят результаты четырех экспериментов. В первых пяти колонках находятся несколько семплов из генератора, а справа находятся наиболее близкие реальные изображения. Из-за использования MLP, результаты на сложных наборах данных пока еще не впечатляющие.
Отметим четыре свойства такого обучения:
- оказывается, что выучивается гладкое и компактное пространство (не путать с математическими понятиями), такое, что прообразы похожих объектов в пространстве шума тоже лежат рядом друг с другом (авторы используют обычный MLP, потому красивые визуализации мы увидим в одной из следующих статей, где используются свёрточные сети), и для любой точки из априорного шума существует осмысленный прообраз;
- генератор выучивается создавать близкие к реальным изображения, ни разу не увидев ни одного реального изображения, а только получая от дискриминатора сигнал о том, почему фальшивка была обнаружена, закодированный в градиентах;
- вроде как пытались избавиться от MCMC, т.к. это занимает много времени, а в итоге получили модель, которая делает семплирование в один шаг, но всё ещё обучается долго и нестабильно (MCMC хотя бы асимптотически сходится, а тут в пространстве параметрических функций никаких гарантий нет);
- модель красивая, но совсем не применимая для извлечения признаков из изображения, что в конечном счете нам и нужно, мы ведь хотим не просто генерировать, но и вычислять прообразы реальных изображений в пространстве шума.
Unsupervised Domain Adaptation by Backpropagation (26 Sep 2014)
Всем вроде было очевидно, что ГАНы это весело и задорно, но пока бесполезно. Пока человечество осознавало, как бы их приспособить для извлечения признаков, в Сколково нашли неожиданное и полезное применение ГАНам. Представьте следующую задачу: необходимо сделать поиск одежды по реальной фотографии из жизни в магазине типа Амазона. Для этого мы легко можем собрать размеченный датасет, просто спарсив Амазон. Затем приписать каждому изображению метку по категории товара, обучить классификатор и использовать какое-либо представление из сети для поиска. Но есть небольшая проблема: все фотографии на амазоне, как правило, являются студийными фотографиями с белым фоном, без шумов и часто вообще без людей. В то время как реальные фотографии, по которым осуществляется поиск, делаются на мобильник и помимо естественных шумов содержат еще людей и богатый фон. Можно было бы, конечно, разметить датасет реальных фотографий, на что было бы потрачено время и деньги, и вообще не факт, что помогло бы.
Такая проблема называется Domain Shift – когда обучение происходит в одном домене, а применение модели происходит в другом. Как правило, распределение данных в доменах разное; цена разметки данных первого домена низкая, а цена разметки данных из второго домена высокая; необходимо обучить такой классификатор, который будет инвариантен к домену, но иметь высокое качество классификации. Другими словами, скрытое представление данных не должно содержать информации о домене, а должно содержать информацию об объекте. И тут-то авторы как раз предлагают использовать ГАНы.
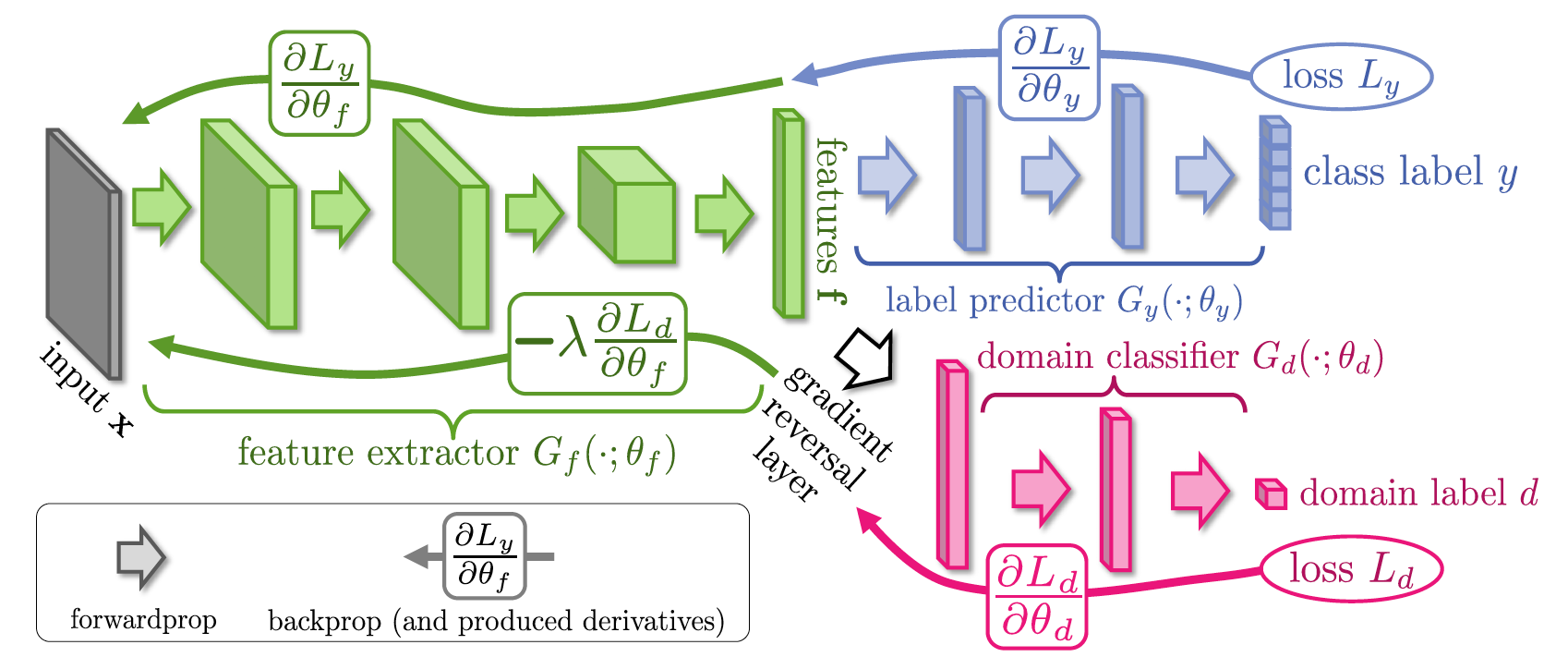
Допустим, мы хотим, чтобы слой f был инвариантен к домену, давайте к нему приделаем еще один классификатор, так же как в Google Inception V1, но будем не минимизировать функцию стоимости, а максимизировать её. Таким образом мы как бы будем "выбивать" информацию о домене из представления f, и "вбивать" информацию об объектах, т.к. обычный классификатор обучается минимизации ошибки классификации между объектами. Оказывается, весь этот процесс обучения можно делать end-to-end, используя gradient reversal layer, который находится между представлением f и доменным классификатором. При обратном распространении ошибки через такой слой знак градиентов инвертируется, таким образом часть сети перед представлением f учится вычислять такие признаки, которые не содержат информации о домене, потому что именно такие признаки максимизируют ошибку классификации доменного классификатора.
Целевая фотография:
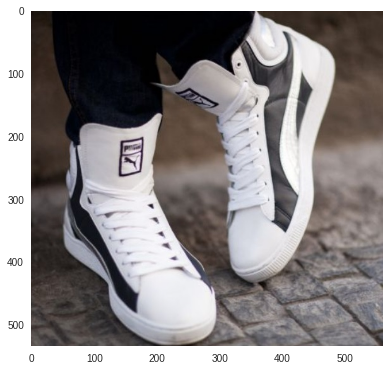
Топ-3 ответов:



Conditional Generative Adversarial Nets (6 Nov 2014)
Спустя полгода после публикации оригинальной статьи про ГАНы люди еще не научились использовать их для извлечения признаков, но уже занялись анализом динамики сходимости минимаксой игры. Было замечено, что если данные мультимодальные, то решение, как правило, коллапсирует в одну моду.

На данном изображении справа вы видите целевое распределение данных, а в левой части вы можете наблюдать процесс сходимости обычного ГАНа. В результате модель выбирает понравившуюся ей моду и генерирует семплы только из неё. Например, вы можете начать тренировать модель генерировать рукописные цифры из множества MNIST, а она выучится отлично генерировать только семерки. Немного не то, что хотелось бы получить. В случае MNIST, когда у нас есть размеченный датасет, авторы предлагают подавать в генератор и дискриминатор не только сгенерированный образ, но и его метку.
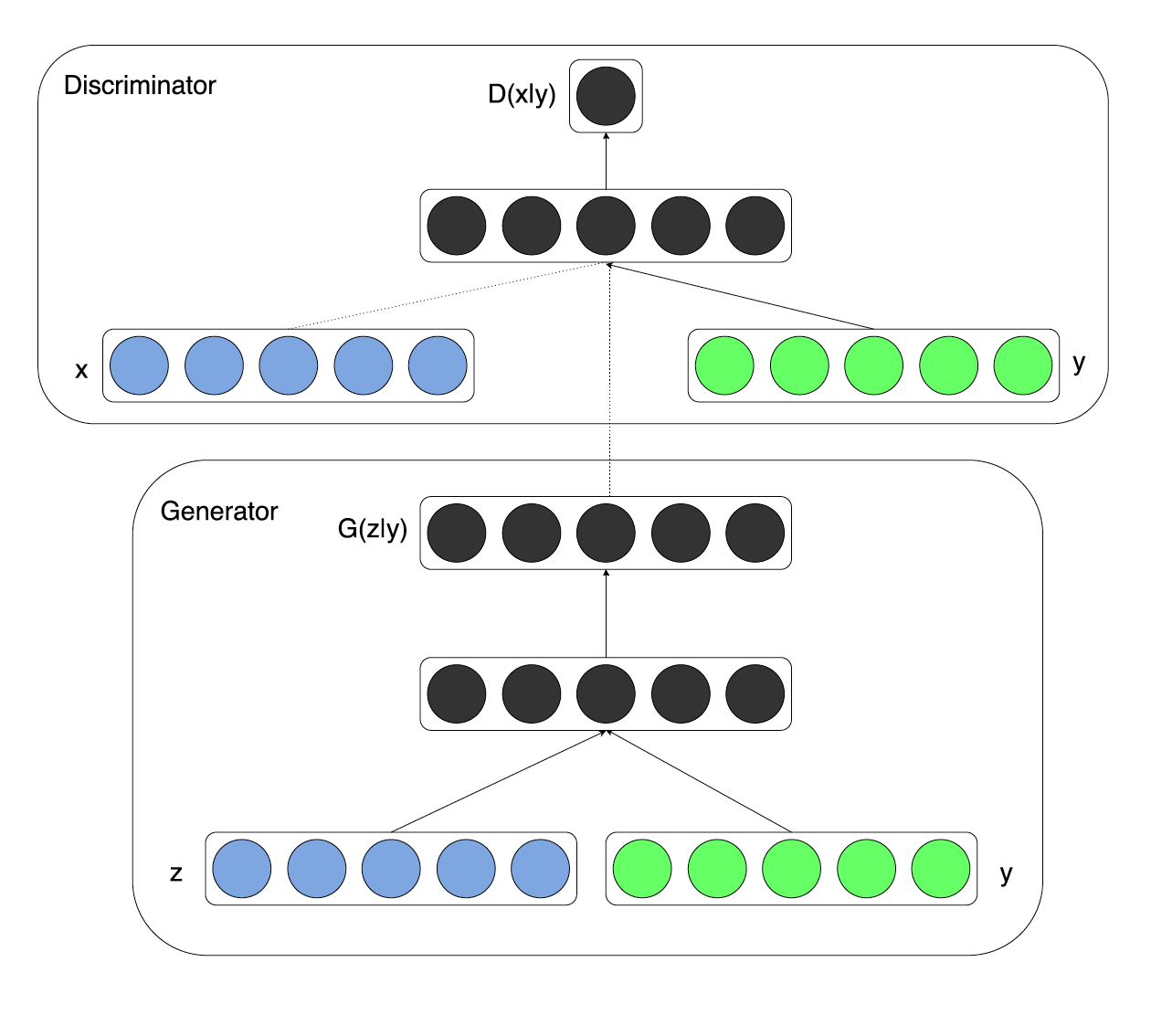
Попробуйте найти два отличия новой функции стоимости от оригинальной:
В результате чего, надеются авторы, произойдет распутывание (disentanglement of factors) моды и других параметров объекта. В случае с рукописными цифрами наблюдается забавный эффект: модели теперь не требуется кодировать информацию о метке (цифре) в вектор признаков (во входной шум), т.к. вся информация уже есть в векторе меток 

Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks (9 Nov 2015)
Данная статья имеет больше практическую ценность, чем теоретическую. Даже сами авторы отмечают, что основной вклад статьи следующий:
- обычная нейросеть заменена на сверточную, и в результате проб и ошибок составлена инструкция по тому, как тренировать Deep Convolutional GAN;
- показано на примерах, что дискриминатор, полученный при тренировке DCGAN, является хорошей инициализацией для других классификаторов на этом и схожих доменах (transfer learning в задачу обучения с учителем из задачи обучения без учителя);
- проанализировав фильтры, авторы показали, что можно найти фильтры, которые отвечают за рисование конкретного объекта;
- показано, что генератор имеет интересные свойства, схожие с word2vec (см. пример далее).
Собственно, в самой модели ничего неожиданного нет, и, вероятно, эксперименты по обучению модели как раз и заняли много времени — между статьей по ГАНам и DCGAN прошло больше года (еще, конечно, сыграло свою роль то, что авторы подстраивались именно под ICLR 2016). Вот схема генератора:
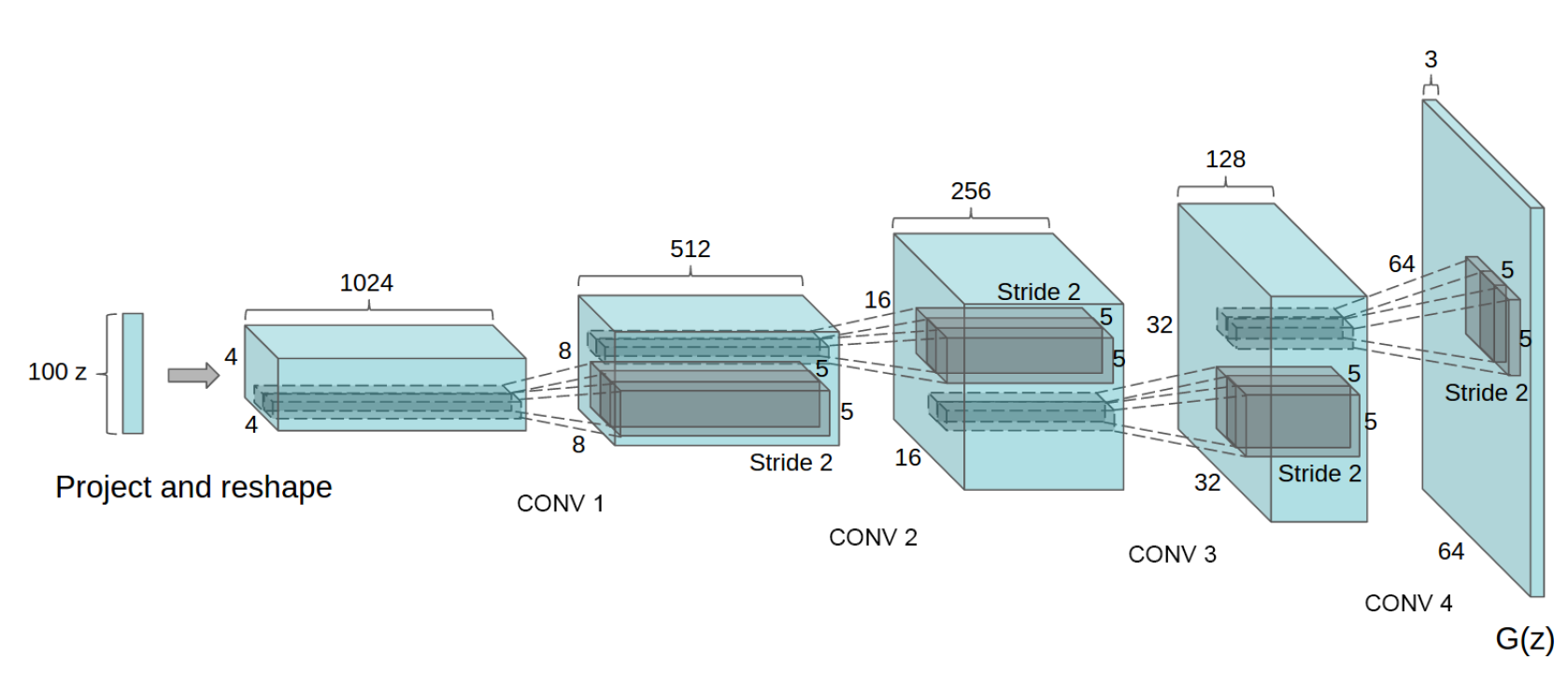
К особенностям архитектуры можно отнести следующие моменты:
- в генераторе и дискриминаторе вместо пулинга используются свертки с шагом больше единицы (stride и fractional stride соответственно);
- батч нормализация используется в генераторе и дискриминаторе;
- не используются полносвязные слои, т.е. сеть становится fully convolutional;
- в генераторе везде, кроме выходного слоя, используется ReLU (в выходном — tanh);
- в дискриминаторе везде используется Leaky ReLU.
В результате мы можем наслаждаться криповыми лицами и арифметикой над ними. Если точнее, то арифметика делается в пространстве признаков, а потом из полученного вектора генерируется результат.

Отдельно стоит упомянуть детали самого этого эксперимента. Для начала им пришлось насемплировать кучу изображений, затем найти там руками и глазами некоторое количество изображений мужчин в очках, мужчин без очков и женщин без очков. Затем векторы признаков каждой группы усредняются, делается арифметика, и из полученного вектора признаков генерируется новое изображение.
В описании первой статьи я писал, что пространство признаков получается гладким и компактным, т.е. если выбрать случайную точку, которая лежит на многообразии прообразов данных, то вокруг этой точки во всех направлениях будут признаки, образы которых похожи на текущий. Теперь можно выбрать случайно несколько точек в пространстве признаков, затем начать семплировать точки вдоль пути, соединяющего семплы, отрисовывая для каждого семпла его образ в пространстве изображений (да, стрелка там есть лишняя).
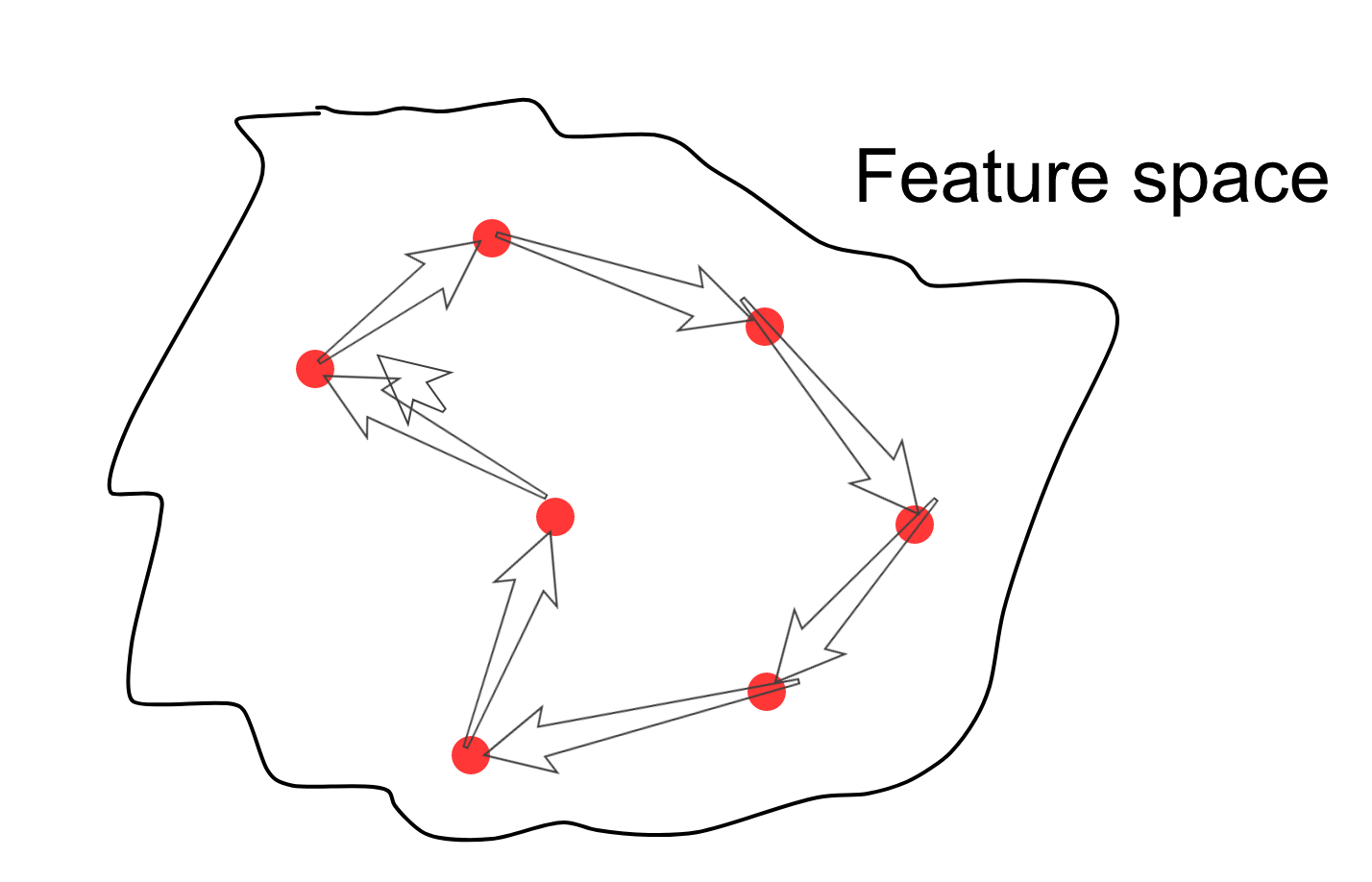
В итоге получатся такие вот переходы одних криповых лиц в другие.

В общем пока в ГАНах явно не хватает механизма извлечения признаков из изображений. И тут-то мы переходим ко второй важнейшей статье после оригинальной статьи про ГАНы — "Adversarial Autoencoders".
Adversarial Autoencoders (18 Nov 2015)
Вторая важнейшая статья в ГАНах появилась полтора года спустя после оригинальной статьи, что опять же связано с тем, чтобы подстроиться под ICLR 2016. В этой статье авторы по сути разворачивают оригинальный и бесполезный ГАН наизнанку и добавляют еще одну функцию стоимости, как в Google Inception V1. В итоге получается особый тип автоэнкодеров — модель, с помощью которой можно извлекать признаки из объектов. Рассмотрим топологию модели AAE и затем обратим внимание на некоторые свойства признаков такого автоэнкодера.
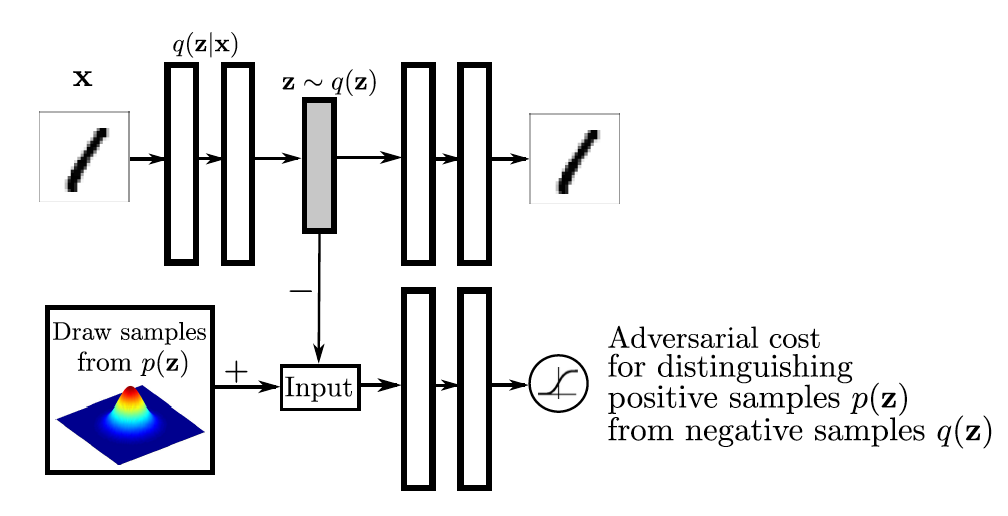
В верхней части изображения находится обычный автоэнкодер. Обозначим распределение, генерируемое энкодером (кодировщиком) как 




Слева снизу находится генератор семплов из некоторого априорного распределения шума. Это может быть как заданное аналитически распределение типа многомерного нормального, так и распределение неведомой природы, некоторый черный ящик. Мы пока не понимаем, как именно он работает, но можем семплировать из него. Обозначим априорное распределение скрытого слоя как 




В результате получается автоэнкодер с двумя функциями стоимости: обычной для качества данных и ГАН для качества скрытого слоя. Обучение модели происходит стохастическим градиентным спуском по следующему сценарию:
- фаза восстановления: обычная итерация обучения автоэнкдера, в процессе которой обновляются параметры энкодера и декодера для минимизации ошибки восстановления образа;
- фаза регуляризации: итерация обновления энкодера и дискриминатора. Она в свою очередь состоит из двух фаз, описанных в сценарии обучения обычных ГАНов, т.е. нужно сначала сделать несколько шагов обучения дискриминатора на батчах из реальных и поддельных примеров при фиксированном генераторе, затем сделать один шаг обучения генератора на батче из поддельных изображений при фиксированном дискриминаторе.
После такого обучения можно надеяться, что сеть обучится отображать образы из пространства данных на заданное нами распределение, а также для любой точки из заданного распределения над кодом находить адекватный образ в пространстве наблюдений.
В самом начале поста есть дерево таксономии генеративных моделей, обратите внимание на вариационный автоэнкодер (VAE), который аппроксимирует явно заданное распределение скрытого слоя. VAE минимизирует верхнюю границу отрицательного логарифма правдоподобия данных:
Переводя на русский, функция стоимости содержит как ошибку восстановления, так и штраф за то, что распределение выхода энкодера отличается от заданного априорного 
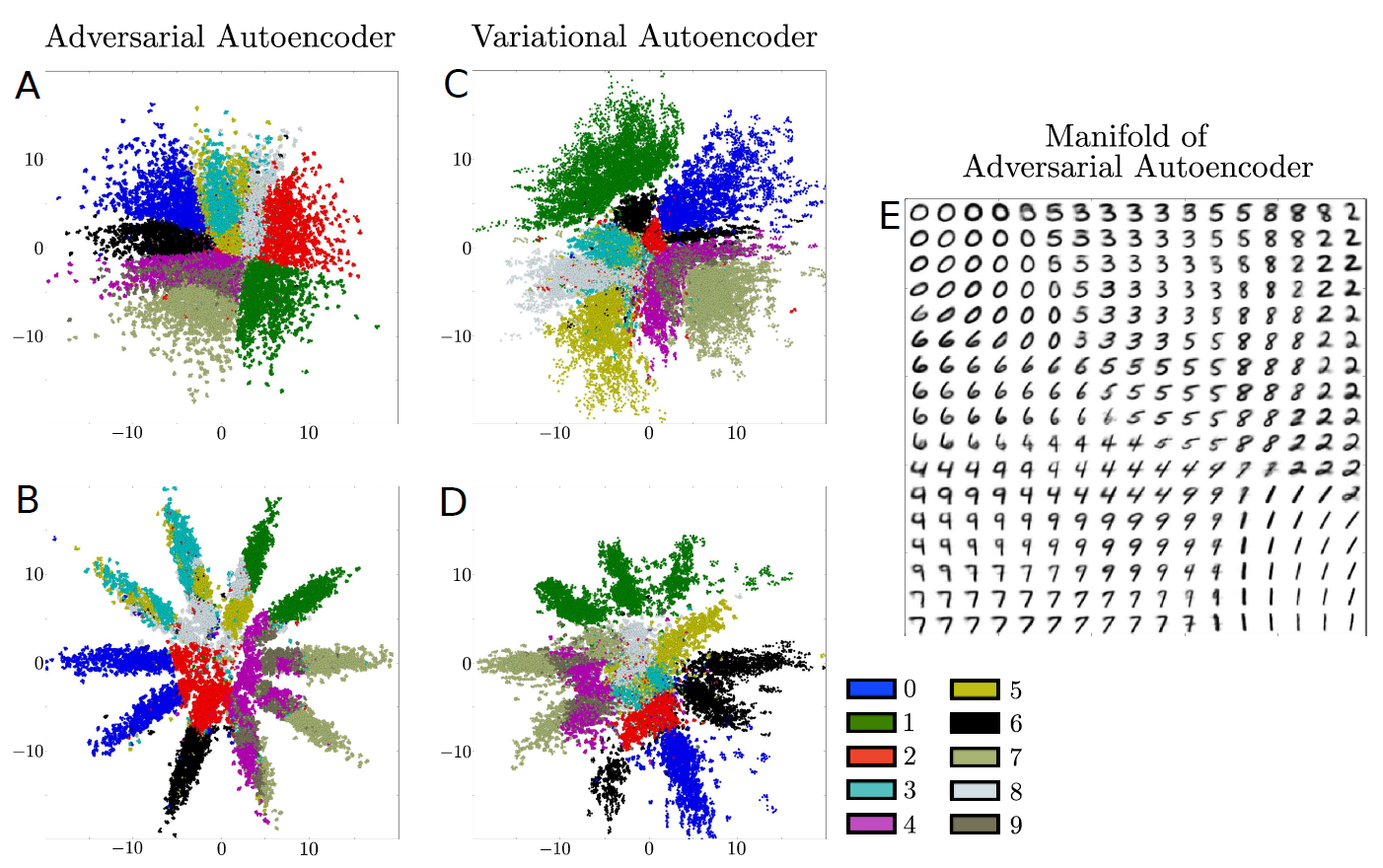
На данном изображении авторы сравнивают то, как ложатся на скрытое пространство примеры с помощью AAE и VAE. В первой строке скрытым пространством является двумерная гауссиана, а во второй строке смесь из десяти гауссиан. Справа авторы семплируют точки из скрытого пространства и отрисовывают соответствующие им изображения рукописных цифр, как видим всё действительно компактно и гладко.
Так же в этой статье описывается несколько более извращенных моделей на основе AAE, которые лягут в основу многих другие моделей в будущем.
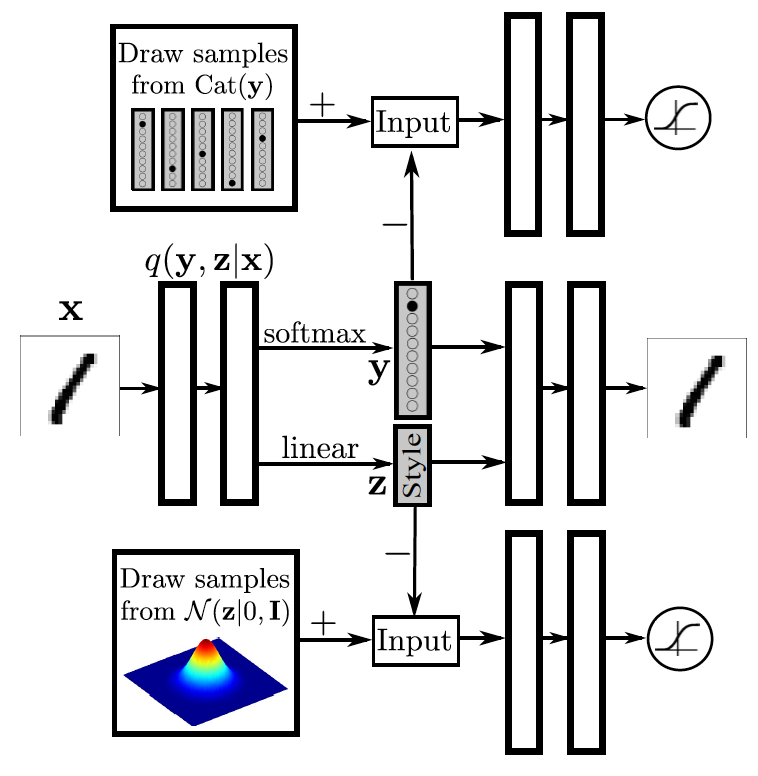
Модель очень похожа на Conditional GAN, но так же вывернутый наизнанку. В центральной части автоэнкодера находится скрытое представление составленное из двух векторов. Первый отображает распределение вероятности принадлежности к классу. Второй отображает некоторое представление стиля (что же еще может остаться, если убрать из написания цифры саму цифру). В верхней части находится ГАН часть для представления класса, которая старается приблизить выданное энкодером (генератором) распределение над классами к реальному one-hot-encoding этой цифры. Нижний ГАН старается вжать информацию о стиле в какое либо распределение (в данном случае в гауссиан). В итоге происходит распутывание информации о классе и стиле. Например, можно зафиксировать класс и генерировать цифру разными стилями. Или же наоборот, фиксируем стиль и отрисовываем разные цифры. Стоит отметить, что в статье они не приводят таких примеров, а вот в следующий статье этого разбора этот эксперимент вполне успешен.
Такая модель полезна, если у вас есть некоторое количество размеченных примеров и намного большее количество неразмеченных (как часто и бывает). Тогда для примеров без метки не используется верхний ГАН.
После этой статьи астрологи объявили несколько лет ГАНов. В целом все статьи после AAE можно разделить на скорее инженерные и скорее теоретические. Первые, как правило, эксплуатируют различные топологии, похожие на распутывание стилей в AAE. Вторые больше концентрируются на теоретических особенностях ГАНов. Мы рассмотрим несколько теоретических и несколько инженерных статей. Для тех, кто решит заняться практической реализацией, будет очень полезно взглянуть на статью автора ГАНа, сделанную на основе его туториала по ГАНам на конференции NIPS в 2016 году: Improved Techniques for Training GANs.
InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets (12 Jun 2016)
Данная статья является представителем теоретической группы статей, в ней авторы добавляют в процесс обучения некоторые информационно-теоретические ограничения, тем самым лучше распутываются скрытые факторы. Авторы рапортуют об успешном распутывании стиля и написанных символов, фона изображений от объекта интереса, а также причесок, эмоций и факта наличия очков на датасете из селфи. Также авторы утверждают, что полученные признаки в режиме обучения без учителя сравнимы по качеству с признаками, полученными обучением с учителем. Не забывают авторы и упомянуть о том, что генеративные модели являются доминирующим типом моделей в сфере обучения без учителя и напоминают, что умение создавать объекты влечет за собой полное понимание структуры объекта и как следствие улучшенное распутывание факторов.
Если кратко, то все эти прелести достигаются за счет максимизации взаимной информации между наблюдениями и некоторым подмножеством признаков из внутреннего представления автоэнкодера. Обычные ГАН не накладывают ограничения на вектор скрытого представления, тем самым, в теории, генератор может начать использовать факторы в очень нелинейно или связано, тем самым ни один из факторов не будет отвечать за какой либо семантический признак (вспомните eigenfaces). Перед тем как перейти к деталям InfoGAN, позвольте мне напомнить вам целевую функцию из оригинального ГАНа:
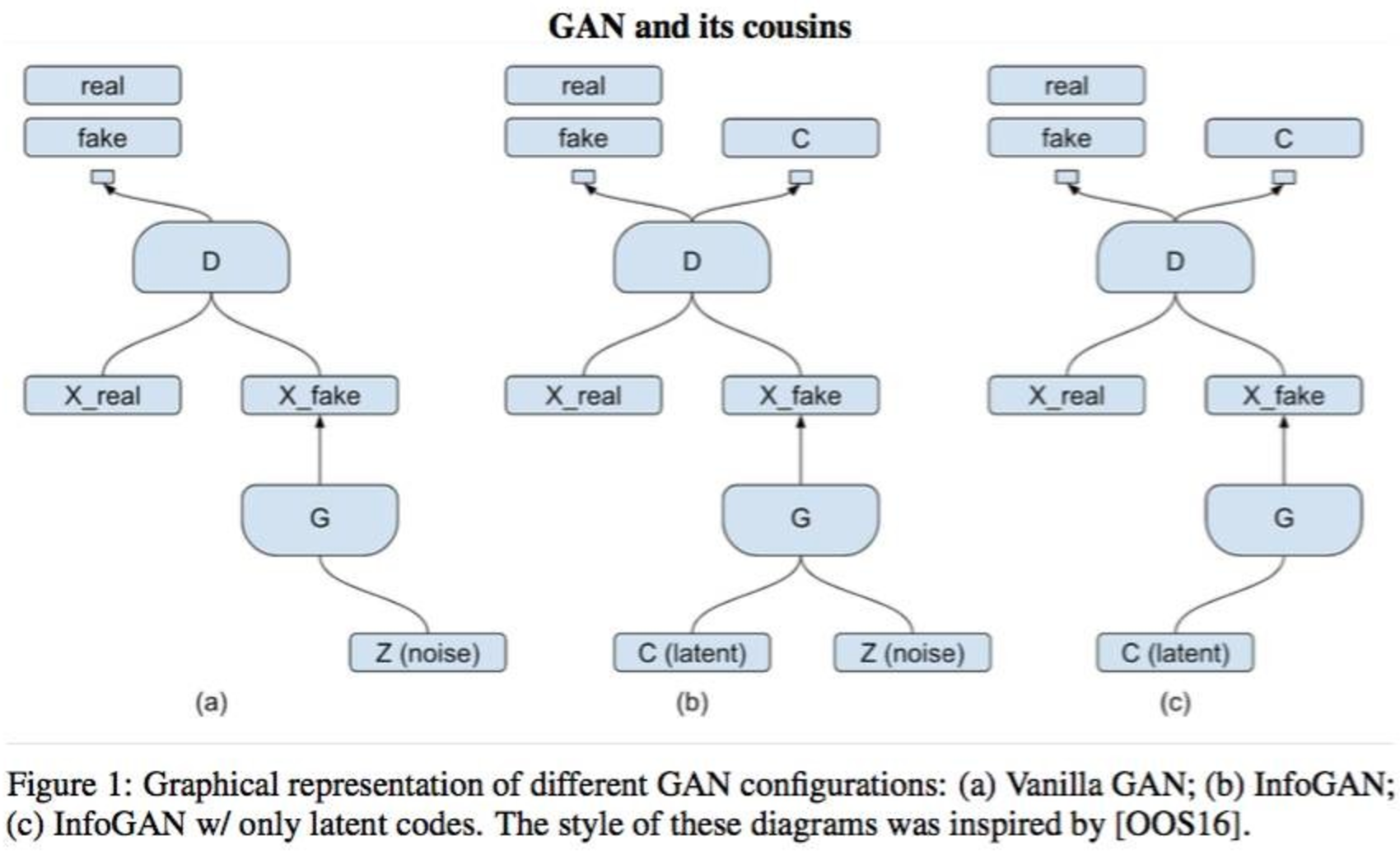
Топология модели идентична модели, описанной в Conditional GAN, скрытый слой разделен на две части: 






Вспомним, что такое взаимная информация. Рассмотрим две случайные переменные 

измеряет "количество информации", полученное о переменной 




Но, к сожалению, такая оптимизационная задача становится нетривиальной из-за того, что теперь нам требуется апостериорное распределение 

KL-дивергенция не отрицательна, а энтропию скрытого семантического слоя можно считать постоянной, тогда получается нижняя вариационная граница взаимной информации. Оптимизируя нижнюю границу, мы оптимизируем и само значение функции, хотя зазор между оценкой и реальным значением определяется дивергенцией и энтропией. И, естественно, распределение 
Таким образом, дискриминатор выполняет две функции: распознавание реального примера от фальшивого и восстановление вектора факторов 
В эксперименте на MNIST — база из десяти рукописных цифр, в качестве скрытого слоя используется одна категориальная переменная как семантическое описание 


В каждой колонке находятся семплы при фиксированной категории, но со случайной шумовой составляющей. В каждой строке наоборот. Слева результаты InfoGAN'а, видно, что в семантической переменной находится информация о лейбле (напоминаю, лейблы не участвовали в обучении). Справа обычный ГАН и нет интерпретации.

А здесь, в каждой строке фиксированы две из трех скрытых переменных, все семплы из InfoGAN'а. Слева фиксируем категорию и вторую шумовую переменную, справа категорию и первую шумовую переменную, и в результате видим, что в шумовой составляющей находится информация о стиле.

Unsupervised Cross-Domain Image Generation (7 Nov 2016)
Давайте рассмотрим теперь статью, которая является скорее инженерной, нежели теоретической. Под инженерной я подразумеваю способ построения модели, использующий "механизмы" (нужно перейти реку — строим мост). Теоретические (в моей нотации) — это модели, где математический трюк позволяет достичь цели. Данная статья является адским миксом стилевого трансфера и ГАНов. Представьте, что есть два датасета из разных доменов Source и Target, например, домены реальных лиц и рисованных эмоджи. Задачей является построение модели, которая может конвертировать семплы из одного домена в другой. Получается, вообще говоря, описание обычного стилевого трансфера. Тогда добавим еще одно требование, чтобы попасть в условия ГАН-задачи: семпл, трансформированный из S в домен T должен быть неотличим от семплов из домена T. Полученную модель назовут Domain Transfer Network. Как я уже сказал, это модель, которая создается модульно из всем до этого известных компонентов. Нам понадобится некоторая функция 




Первая базовая модель, которую создали авторы, следует напрямую из условия задачи. У нас есть генератор 


Но такое прямолинейное решение не заработало. Тогда авторы, вероятно, что-то употребили и создали следующего монстра.
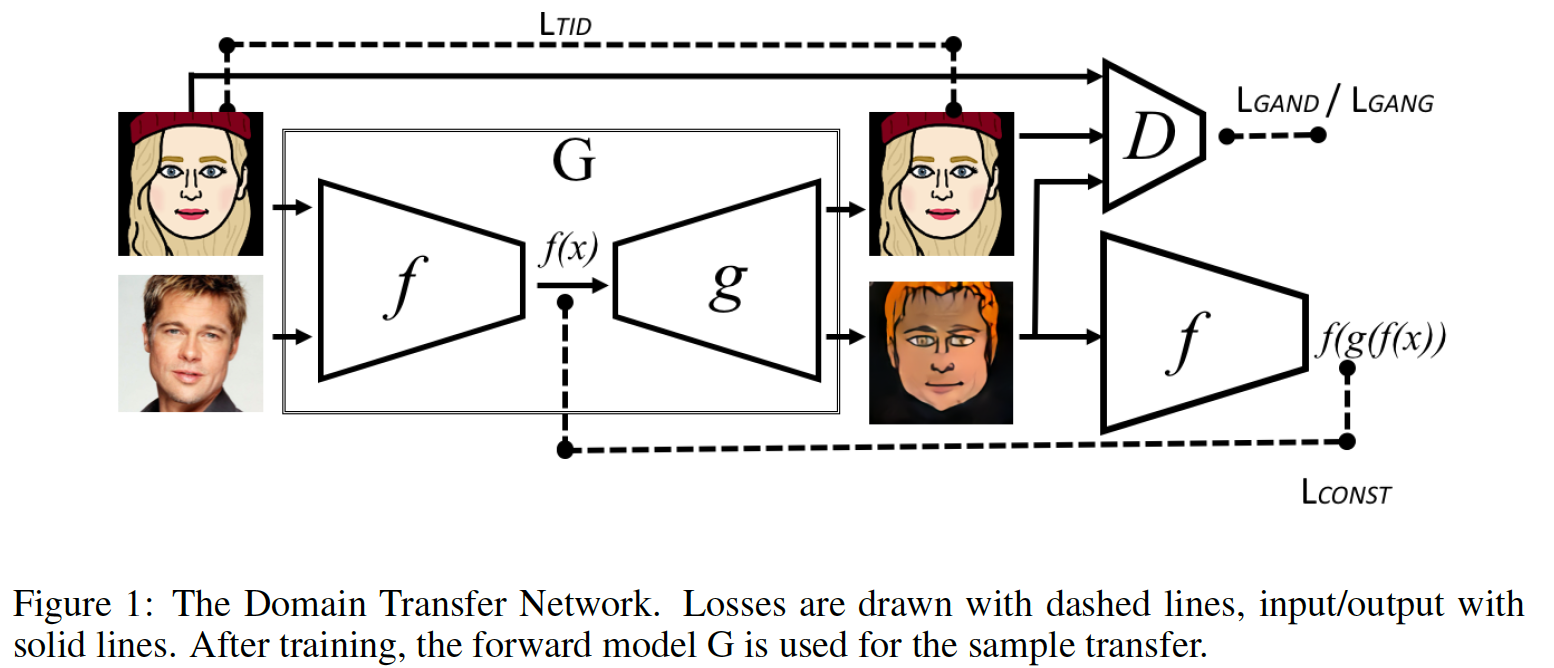
Генератор 


Дискриминатор 
- семпл из домена T под действием
- семпл из домена S под действием
- семпл из домена T в чистом виде
Функция стоимости генератора тоже состоит из нескольких:
- третий класс дискриминатора отвечает за чистые семплы из домена T, его-то и учится обманывать генератор
- f-constancy loss, отвечающий за инвариантность энкодера для семплов из домена S
- для семплов из домена T мы хотим, чтобы генератор
их никак не изменял
- для семплов из домена T мы хотим, чтобы генератор
- total variation loss добавляет немного размытия на изображение,
— это пиксели изображения на выходе из генератора
- total variation loss добавляет немного размытия на изображение,
Функцию 

- рукописные цифры в знаки на домах
- эмоджи в реальных людей :wat:

Проблема такой сети в том, что у вас вряд ли получится её натренировать. Все дело в том, что жадный FB не выложил базу эмоджи. Я лично пробовал обучать на базе аниме персонажей (да, каюсь, пришлось спарсить 100к картинок с японскими порномультиками, распознать там то, что называется лицом, и попробовать обучить). Результат вообще никакой, вероятно из-за того что "физика" лица в онеме совсем не реальная.
Unrolled Generative Adversarial Networks (7 Nov 2016)
В данной статье авторы пытаются решить проблему коллапсирования генератора в моду распределения данных. В отличие от предыдущей статьи, авторы подходят к проблеме, анализируя математику процесса обучения ГАНов. Для начала рассмотрим, почему происходит коллапсирование в моду распределения. Допустим, у нас есть бимодальное распределение, и дискриминатор пытается различать семплы: являются ли они примерами из этого распределения или все таки подделки. Также допустим, что у этого бимодального распределения одна мода в два раза плотнее другой. Оптимальной стратегией генератора будет постоянная генерация примера из точки с наибольшей плотностью, т.е. из той моды, которая больше. Получается, что бы мы не подали на вход такого генератора, мы всегда будем получать примерно одинаковые образы. Наверное. "Наверное" — потому что это не доказано, но звучит вполне правдоподобно. Обозначим параметры генератора и дискриминатора, как 

целью будут оптимальный генератор:
где оптимальный дискриминатор является функцией от генератора:
Для фиксированного генератора можно выучить хороший (в смысле локального оптимума) дискриминатор градиентным подъемом (третья формула ниже), мы же максимизируем дискриминатор:
Стоит заметить, что весь процесс обучения оптимального генератора можно представить в виде длинной суммы (первая и вторая формулы), и мало того, вся эта сумма будет дифференцируема. Введем суррогатную функцию стоимости на 
Получается, что обучая генератор при 



Таким образом, градиенты для генератора мы берем как будто бы из будущего (разворачиваем ГАН как рекуррентную сеть); затем для нового генератора, который видел будущее, обновляем дискриминатор из настоящего, вследствие чего процесс обучения сильно замедляется, примерно в 
Первый член градиента соответствует обновлению неразвернутого ГАНа, т.е. при фиксированном дискриминаторе 




Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (30 Mar 2017)
Ну и под конец я затрону буквально в нескольких предложениях одну мою самую любимую модель, ибо она проста, элегантна и эффективна. Более подробно про эту модель будет вскоре отдельный пост с матаном и кодом.
Представьте, что у нас есть два домена X и Y, например, селфи мужчин и женщин. Мы хотим сделать модель, которая умеет конвертировать мужчин в женщин, а женщин в мужчин.
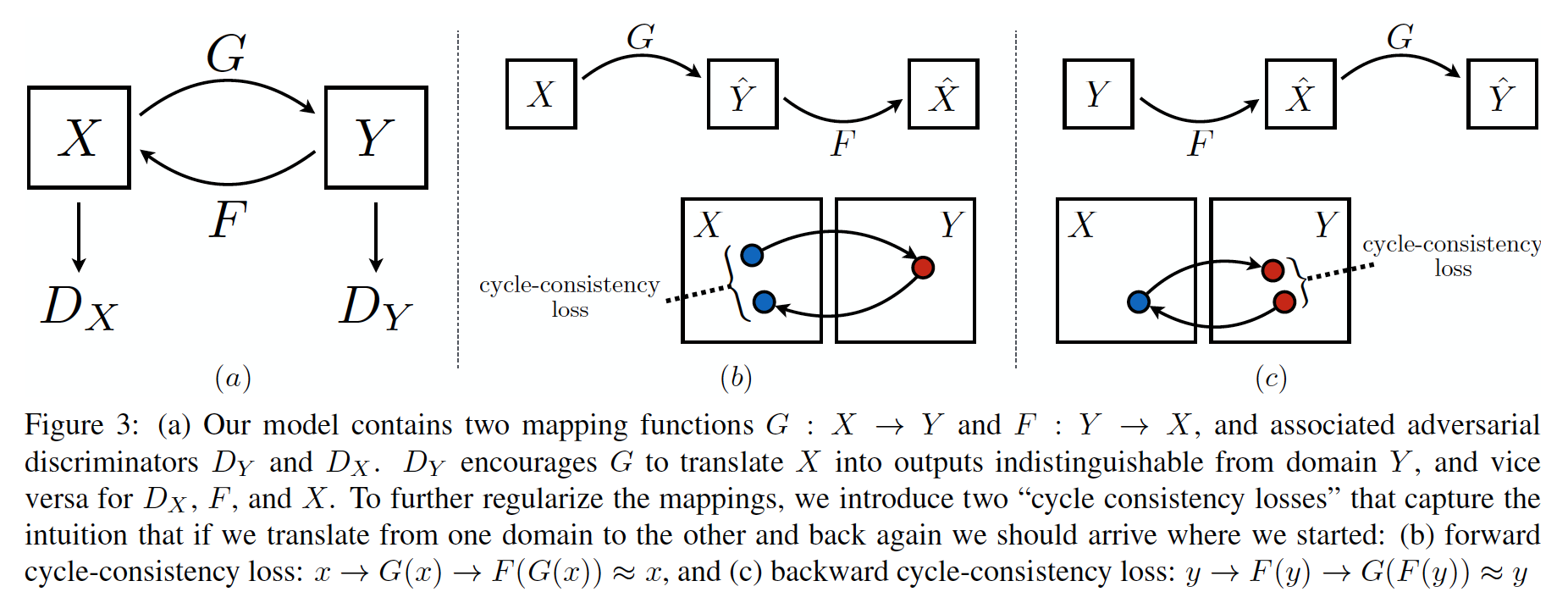
Для этого мы возьмем две сети-генератора 


 |
 |

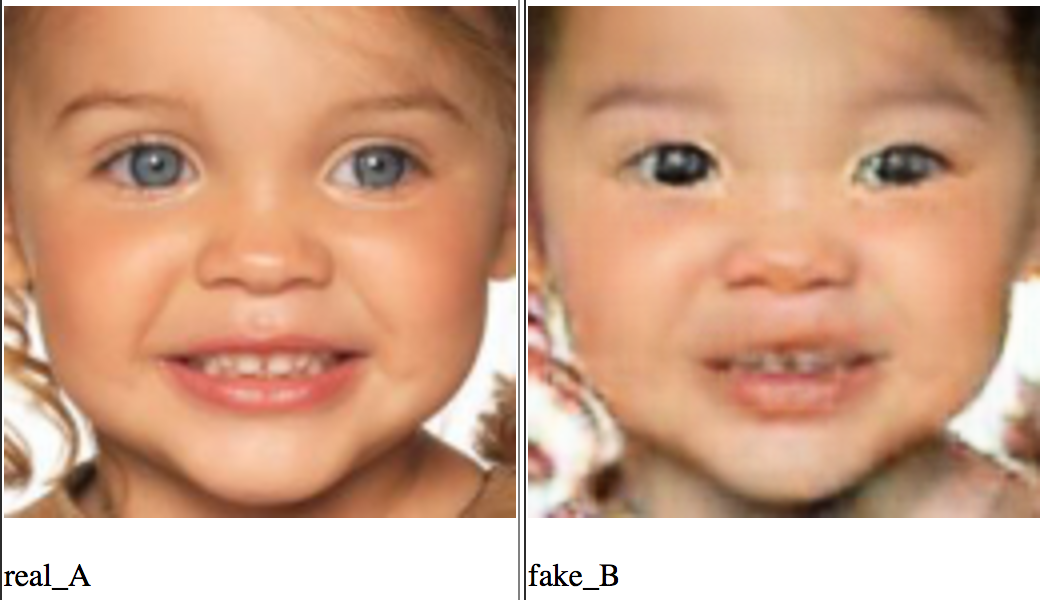


PS: кстати, если вы будете такое делать, то замените попиксельный consistency loss на такой же, но в пространстве VGG признаков, как это делается в задаче style transfer.
В общем, ждите вскоре детального разбора этой сети.
Заключение
На этом на сегодня у меня все. ГАНы уже как год являются одной из самых популярных тем в глубоком обучении. Для тех, кто захочет углубиться в них, вот несколько полезных ссылок:
- https://github.com/zhangqianhui/AdversarialNetsPapers
- https://github.com/nightrome/really-awesome-gan
- https://github.com/wiseodd/generative-models
- а на десерт можете полюбоваться генератором хорроров из MIT.
- а для тех адептов, кто понимает обучение с подкреплением, может быть интересна статья о связи ГАНов и reinforcement learning
Было бы в общем в жизни все так просто как в ГАНах:

Спасибо за правки и советы следующим дамам и господам из ложи датасаентологов: bauchgefuehl, barmaley_exe, yorko, ternaus и movchan74.
Автор: Павел Нестеров



![Нейросетевая игра в имитацию - 28 $large min_G max_D Vleft(D, Gright)=mathbb{E}_{x sim p_{text{data}}left(xright)} left[log Dleft(xright)right] + mathbb{E}_{z sim p_zleft(zright)}left[logleft(1 - Dleft(Gleft(zright)right)right)right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-28.svg)

![Нейросетевая игра в имитацию - 53 $large min_G max_D Vleft(D, Gright)=mathbb{E}_{x sim p_{text{data}}left(xright)} left[log Dleft(x mid yright)right] + mathbb{E}_{z sim p_zleft(zright)}left[logleft(1 - Dleft(Gleft(z mid yright)right)right)right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-53.svg)
![Нейросетевая игра в имитацию - 54 $large min_G max_D Vleft(D, Gright)=mathbb{E}_{x sim p_{text{data}}left(xright)} left[log Dleft(xright)right] + mathbb{E}_{z sim p_zleft(zright)}left[logleft(1 - Dleft(Gleft(zright)right)right)right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-54.svg)
![Нейросетевая игра в имитацию - 72 $begin{array}{rcl} E_{x sim p_dleft(xright)} left[ -log pleft(xright) right] &<& E_xleft[ E_{qleft(z mid xright)}left[-log pleft(x mid zright)right] right] + E_xleft[ text{KL}left(qleft(z mid xright) midmid pleft(zright)right)right] \ &=&E_xleft[ E_{qleft(z mid xright)}left[-log pleft(x mid zright)right] right] - E_x left[Hleft(qleft(z | xright)right)right] + E_{qleft(zright)}left[-log pleft(zright)right] \ &=& text{Reconstruction} - text{Entropy} + text{CrossEntropy}left(qleft(zright), pleft(zright)right) end{array}$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-72.svg)
![Нейросетевая игра в имитацию - 76 $large min_G max_D Vleft(D, Gright)=mathbb{E}_{x sim p_{text{data}}left(xright)} left[log Dleft(xright)right] + mathbb{E}_{z sim p_zleft(zright)}left[logleft(1 - Dleft(Gleft(zright)right)right)right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-76.svg)


![Нейросетевая игра в имитацию - 95 $begin{array}{rcl} Ileft(C, Gright) &=& Hleft(Cright) - Hleft(C mid Gright) \ &=& Hleft(cright) - E_gleft[Hleft(c mid gright)right] \ &=& Hleft(cright) + E_g E_{c mid g} log pleft(c mid gright) \ &=& Hleft(cright) + E_g E_{c mid g} log dfrac{pleft(c mid gright) qleft(c mid gright)}{qleft(c mid gright)} \ &=& Hleft(cright) + E_g E_{c mid g} log qleft(c mid gright) + E_g E_{c mid g} log dfrac{pleft(c mid gright)}{qleft(c mid gright)} \ &=& Hleft(cright) + E_g E_{c mid g} log qleft(c mid gright) + E_g text{KL} left(pleft(c mid gright) mid mid qleft(c mid gright)right) \ &geq& Hleft(cright) + E_g E_{c mid g} log qleft(c mid gright) \ &geq& E_g E_{c mid g} log qleft(c mid gright) end{array}$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-95.svg)











![Нейросетевая игра в имитацию - 135 $large Vleft(theta_G, theta_Dright)=mathbb{E}_{x sim p_{text{data}}left(xright)} left[log Dleft(x; theta_Dright)right] + mathbb{E}_{z sim p_zleft(zright)}left[1 - Dleft(Gleft(z; theta_Gright); theta_Dright)right]$](https://www.pvsm.ru/images/2017/09/04/neirosetevaya-igra-v-imitaciyu-135.svg)











