Измерение интенсивности входящего потока событий в модели распада

в 8:07, , рубрики: C, rate detector, алгоритм определения интенсивности, Алгоритмы, Блог компании Qrator Labs, математика, поток событий, метки: , ,

В классе поточных алгоритмов имеется подкласс, решающий задачу поиска тяжелых элементов (heavy hitters). В общем виде эта задача формулируется как «выявление во входящем потоке наиболее часто повторяющихся событий и измерение их интенсивности». В данной публикации сотрудника компании Qrator Labs Артема janatem Шворина предлагается эффективный алгоритм для решения этой задачи.

Введение

Алгоритмы нахождения тяжелых элементов помогают решать задачи, такие как борьба с перегрузкой сети, выявление сетевых аномалий и атак, управление динамической маршрутизацией. Например, известный веб-сервер NGINX позволяет ограничивать интенсивность запросов к определённому ресурсу, и для того, чтобы это делать, интенсивность должна быть измерена количественно.

В этой публикации мы хотим показать читателю ещё один подход к измерению интенсивности потока событий при наличии множества разных (не идентичных) потоков событий. Пусть задано множество типов событий. Требуется оценивать, насколько часто происходит событие данного типа, и обращать внимание на случаи, когда событие одного типа повторяется «слишком часто».

Важной характеристикой данного инструмента является его высокая эффективность, чтобы он не стал узким местом во всей системе анализа и фильтрации трафика. Речь в этом случае идет о том, чтобы обрабатывать одно событие за несколько десятков тактов центрального процессора современных компьютеров.

Помимо собственно измерения интенсивности требуется выделять типы событий, которые случаются наиболее часто. Их интенсивность нужно измерять более точно, в то время как редкие типы событий большой роли не играют, и оценивать их интенсивность не обязательно с высокой точностью.

В работе представлен разработанный нами алгоритм Decay-based count, основанный на модели распада радиоактивного вещества (см. раздел «Модель распада»), с высокой эффективностью решающий задачу поиска тяжелых элементов.

Задача поиска тяжелых элементов

Классификация задач

В описываемом классе задач можно выделить следующие подклассы:

  • Threshold-$t$. Требуется выделить потоки, имеющую большую интенсивность чем заданная доля $t$ интенсивности всего входящего трафика.
  • Top-$k$. Требуется выделить заданное количество $k$ самых интенсивных потоков.
  • Выделение потоков, интенсивность которых превышает некоторое заданное абсолютное значение.

Предлагаемый алгоритм относится к последнему из перечисленных подклассов.

Целевая архитектура

В зависимости от платформы, на которой предполагается запускать данный поточный алгоритм, имеется набор аппаратных ограничений. Иногда требуется встраивать нужную функциональность в сетевое оборудование (свитч, коммутатор и т. п.). Предлагаемый алгоритм предполагается использовать на универсальном процессоре, но при некоторых значениях параметров допускает встраивание в сетевое оборудование.

Параметры задачи

  • Абсолютное значение интенсивности потока, которое считается «опасным». Задачей алгоритма является выявление потоков, интенсивность которых превышает заданный порог.
  • Размер ключа — идентификатора, по которому определяется тип события. В данной реализации, как и во многих других алгоритмах, требуется хранить значения ключей в таблице, поэтому размер ключа влияет на затраты памяти.
  • Способ вычисления оценки интенсивности одного потока по временам прихода однотипных событий. По сути это алгоритмическое определение того, что такое интенсивность потока. В этом случае вычисляется экспоненциальное скользящее среднее, которое имеет единственный параметр — характерное время $tau$, в течение которого учитывается вес события после его прихода.

Точность решения

  • Оценкой качества алгоритма может быть относительная или абсолютная погрешность в оценке интенсивности потоков. Также используют $(varepsilon,delta)$-аппроксимацию в качестве оценки точности: если с вероятностью $1-delta$ погрешность составляет не более $varepsilon$, то говорят, что алгоритм имеет характеристику точности $(varepsilon, delta)$.
  • Если ошибка имеет качественный, а не количественный характер, как, например, включение или невключение данного потока в список самых интенсивных в задаче top-$k$, то для оценки берутся вероятности ложноположительного и ложноотрицательного срабатывания.

Накладные расходы

Как правило, основной характеристикой алгоритма является максимальная интенсивность входящего потока, которую он способен обработать. То есть важно лишь время обработки одного события. Однако на практике влияют и другие аппаратные ограничения, такие как размер памяти, используемой для хранения накопленной информации о потоке. Особенно жесткие аппаратные ограничения имеют место при встраивании функционала в сетевое оборудование. Но и на обычных компьютерах наличие большого количества оперативной памяти DRAM помогает далеко не всегда, поскольку доступ в DRAM может занимать неприемлемо много времени. Для того чтобы достичь требуемой производительности, приходится идти на компромисс с точностью измерения и ограничивать размер используемой памяти, чтобы она помещалась в кэш процессора. В данной реализации при осмысленных значениях параметров таблица помещается в L2 кэш процессора. В результате удалось добиться того, чтобы время обработки одного события составляло несколько десятков тактов процессора.

Методы оценки интенсивности потока

Для оценки интенсивности повторений событий заданного типа требуется посчитать количество событий в течение некоторого времени. Для этого нужно фиксировать время наступления события и каким-то образом сохранять его. Обычно для этой цели используют счетчик, который инкрементируется при наступлении соответствующего события. Тогда интенсивность оценивается как отношение значения счетчика к интервалу времени, в течение которого проводится измерение. Более аккуратные способы измерения актуального значения интенсивности используют различные варианты скользящего среднего. Например, экспоненциальное скользящее среднее (exponential moving average, EMA) — разновидность взвешенного скользящего среднего с экспоненциально убывающими весами.

В работе предлагается новый метод вычисления EMA. Здесь используется модель экспоненциального распада, которая описывает такое физическое явление как радиоактивный распад. Эта модель имеет ряд преимуществ по сравнению с традиционным подходом. Во-первых, представление данных оказывается более экономичным по памяти. Во-вторых, модель распада допускает эффективную по скорости реализацию операции обновления счетчика — она требует небольшое количество целочисленных арифметических операций и одно кэшируемое обращение к памяти.

Методы учета множества потоков

В задаче поиска тяжелых элементов проблемой является не только высокая интенсивность входного трафика, но и большое количество различных потоков (типов событий), за которыми приходится следить. Наивная реализация предполагает заведение отдельного счетчика на каждый поток, что приводит к значительному расходу памяти. При этом есть опасность не только в исчерпании всей доступной памяти, но в существенной замедлении скорости работы из-за промахов в кэш. Поэтому, как правило, отказываются от точного решения задачи поиска тяжелых элементов, выбрасывая часть накопленной информации о потоках. Известно множество методов ограничения объема используемой памяти и уменьшения времени обработки события, некоторые из которых приведены ниже:

  • Packet sampling
  • Space saving algorithm
  • HashParallel
  • HashPipe
  • Count-min sketch

Формализация задачи

Прежде чем переходить к описанию алгоритма, необходимо с достаточной математической строгостью сформулировать задачу измерения потока событий, что мы и сделаем в данном разделе.

Последовательность однотипных событий задается в виде множества элементарных событий ${event_k}_{kin I}$, где индекс $k$ пробегает конечный или бесконечный дискретный интервал $Isubsetmathbb{Z}$.

В простейшем случае событие определяется только временем его наступления: $event_k=t_k$, причем события упорядочены во времени: $t_{k_1} < t_{k_2}$ для $k_1<k_2$. В большинстве реализаций систем учета событий время считается дискретной величиной: $t_kinmathbb{Z}$, однако для теоретических рассуждений бывает удобно обобщить и считать время непрерывным: $t_kinmathbb{R}$.

Основной вопрос, на который должны отвечать системы учета событий, — это оценка интенсивности потока. Интенсивность может быть строго формализована для равномерного потока событий. Равномерный поток ${t_k}$ определяется следующим образом:

$t_k=varphi+pk,quad kinmathbb{Z},$

где $p>0$, $varphiin[0,p)$ — параметры потока — период и фаза, соответственно. То есть события наступают через равные промежутки времени. Тогда интенсивность такого потока, по определению, выражается как $r=1/p$.

Для неравномерных потоков формальное определение интенсивности $r=r({t_k})$ может отличаться в зависимости от постановки задачи. Модель распада остается работоспособной и полезной и в этом случае, однако оценка качества вычисления истинной интенсивности дана ниже только для случая равномерных потоков.

В некоторых моделях требуется дополнительно учитывать некоторую характеристику события, например, его вес $c_k$ — величина вклада данного события в измеряемую интенсивность. Тогда событие определяется не только временем его наступления, но и весом: $event_k=(t_k, c_k)$.

В типичных реализациях систем учета событий заводится счетчик $s$, который некоторым образом накапливает информацию о потоке событий, и в любой момент времени по его текущему значению можно получить оценку интенсивности потока $hat{r}=hat{r}(s)$, такую что $rapproxhat{r}$. Обновление счетчика происходит по приходу очередного события $event_k$:

$s leftarrow update(s, event_k),$

где $update()$ — некоторая функция, которая определяется реализацией. Ниже приведено несколько примеров с вариантами реализации функции $update()$:

  • Простой подсчет количества событий: $update_1(s, event_k)=s+1$;
  • Подсчет количества событий с учетом веса: $update_c(s, event_k)=s+c_k$;
  • Вычисление экспоненциального скользящее среднего (EMA) с параметром $beta$. Здесь счетчик $s=(v,t)$ хранит две величины: собственно значение EMA и время последнего обновления.

    $update_{EMA}((v, t), event_k)=(v', t'),$

    где $v'=beta + (1-beta)^{t_k-t}cdot v,quad t'=t_k$.

В некоторых задачах требуется различать потоки событий. Пусть имеется множество различных типов событий, занумерованных индексом $i=1,dots N$, и требуется учитывать отдельно потоки сообщений каждого типа. Тогда событие описывается как $event_k=(t_k, i_k)$ (или, с учетом веса события, $event_k=(t_k, i_k, c_k)$), где $i_k$ — тип события. Множество индексов $k$, относящихся к данному типу события $i$ обозначим $I_i={kmid i_k=i}$.

Модель распада

Модель распада описывается следующим образом:

$v(t)=v_0 e^{-lambda t},$

где $v_0$ — «количество вещества» в нулевой момент времени, $v(t)$ — количество в момент времени $t$, $lambda$ — параметр модели (так называемая постоянная распада). Название данной модели отражает тот факт, что она описывает физическое явление радиоактивного распада.

Дополнительно введем следующие обозначения:

$tau=1/lambda,quadalpha=e^{lambda}.$

В нашем случае в качестве параметра модели вместо $lambda$ удобнее использовать $tau$, поскольку $tau$ будет иметь размерность времени и неформально может определяться как характерный интервал времени, в течение которого собирается история событий.

Будем по определению считать, что каждому типу события соответствует величина $v$, имеющая физический смысл «количества вещества» и зависящая от времени, которая при наступлении события скачком увеличивается на единицу, а в остальное время уменьшается по приведенному выше экспоненциальному закону.

На рис. 1 показано, как меняется со временем значение $v$ для равномерных потоков с разной интенсивностью и для неравномерного потока.

Измерение интенсивности входящего потока событий в модели распада - 58

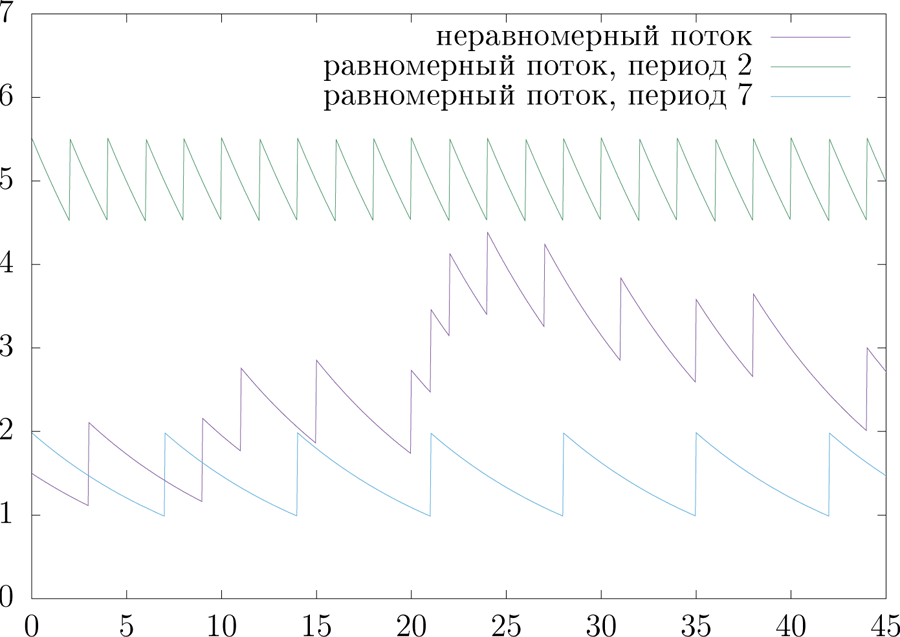
Рисунок 1: Значение $v$ для разных потоков

Величина $v$ не хранится явно в памяти, но может быть вычислена в любой момент. Хранится же значение $s$, такое что в момент времени $t_{now}$ величина $v$ выражается следующим образом:

$v=alpha^{s-t_{now}}.$

Данное представление соответствует модели распада.

Вычисление счетчика в модели распада эквивалентно вычислению экспоненциального
скользящего среднего с точностью до нормирующего множителя (константы). Важной особенностью данного представления является то, что единственное значение, хранимое в счетчике, заменяет собой пару (время последнего события, накопленная величина), которую хранят при традиционном подходе.

Обновление счетчика

Нетривиальной операцией является обновление значения счетчика $s$ при наступлении очередного события. В этом случае требуется заменить $s$ на новое значение $s'$, которое определяется из следующего равенства:

$alpha^{s'-t_{now}}=alpha^{s-t_{now}} + 1.$

Здесь слева стоит значение $v$ сразу после наступления события, а справа — значение $v$ непосредственно до события, увеличенное на вклад события (равный единице). Ниже будут предложены эффективные способы вычисления результата обновления.

В терминах функции $update()$ из определения операция обновления выражается так:

$update_1(s, event_k)=t_k + log_alpha(1 + alpha^{s-t_k}).$

Здесь время исполнения операции $t_{now}$ совпадает со временем $t_k$ прихода сообщения.

Определение интенсивности

Пусть имеется равномерный поток событий интенсивности $r$, то есть события наступают с периодом $p=1/r$. Равномерный поток задается согласно определению.

Если измерение производится сразу после наступления очередного события, то есть $t_{now}=t_n$ для некоторого $n$, то накопленное в течение длительного времени значение счетчика $s$ будет выражаться следующим рядом:

$alpha^{s-t_{now}}=sum_{k=-infty}^nalpha^{t_k-t_{now}}=sum_{k=0}^infty alpha^{-kp},$

откуда

$alpha^{-Delta s} + alpha^{-p}=1,$

где $Delta s=s-t_{now}$ — относительное значение счетчика.

В более общем случае момент измерения может оказаться между событиями:
$t_{now}=t_n+psi$, $psiin[0,p)$. В этом случае значение счетчика будет отличаться в меньшую сторону на величину $psi$:

$alpha^{-(Delta s+psi)} + alpha^{-p}=1.$

Задача измерения интенсивности заключается в том, чтобы по значению счетчика оценить интенсивность. В предположении, что поток равномерный, можно получить оценки истинной интенсивности равномерного потока сверху и снизу, подставляя в предыдущее уравнение крайние значения $psi=0$ и $psi=p$:

$r^-le r < r^+,$

где

$begin{align}r^+&=r^+(Delta s)=frac1{log_alpha(1+alpha^{-Delta s})}\r^-&=r^-(Delta s)=left{begin{array}{ll}frac1{-log_alpha(1-alpha^{-Delta s})}&mbox{при }Delta s>0\ 0&mbox{иначе}end{array}right.end{align}$

Обе оценки $r^+$ и $r^-$ монотонно зависят от значения счетчика $s$ (см. рис. 2), поэтому, например, сравнение текущего значения счетчика с пороговым значением не требует дополнительных вычислений.

Измерение интенсивности входящего потока событий в модели распада - 94

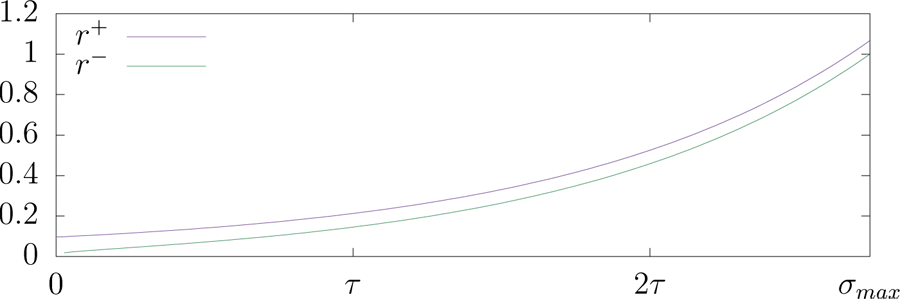
Рисунок 2: График функций $r^-$ и $r^+$ для $tau=15$

В модели распада интенсивность произвольных (не обязательно равномерных) потоков по определению задается приведёнными выше оценками $r^+$ и $r^-$. Причем, если измерение происходит сразу после обработки события, то интенсивность считается в точности равной нижней оценке.

Границы применимости модели распада

Существуют ограничения на значение интенсивности, которая может быть корректно измерена в модели распада.

Во-первых, если время наступления событий измеряется как дискретная величина, то период потока не может быть меньшим единицы. То есть интенсивность потока не должна превышать $r_{max}=1$. Отсюда следует ограничение на относительное значение счетчика $Delta s=s-t_{now}$ — оно не должно превышать значения $sigma_{max}$, которое определяется из формулы:

$r^-(sigma_{max})=r_{max}.$

Величина $sigma_{max}$ оценивается следующим образом:

$sigma_{max}=taulntau+omega(tau),$

где $0leomega(tau)le1/2$.

Во-вторых, оценка интенсивности слабых (малоинтенсивных) потоков затруднена: при малых относительных значениях счетчика $Delta s$ точность верхней и нижней оценки $r^+$ и $r^-$ ухудшается, а при отрицательных значениях $Delta s$ нижняя оценка интенсивности вырождается в нуль.

Также есть ограничение на время работы реализаций модели распада, связанное с переполнением счетчиков. Поскольку значение счетчика не может убежать от $t_{now}$ более, чем на $sigma_{max}$, время работы системы фактически определяется разрядностью счетчика и длительностью одного такта. Если для хранения счетчика используется 64-разрядный регистр, то он не переполнится в течение 100 лет. Но в реализациях с малоразрядными регистрами должен быть предусмотрен механизм сброса счетчиков.

Алгоритмы учета множества потоков

Особенности модели распада

Особенностью использования EMA в качестве значения счетчика является то, что при прекращении потока событий накопленное значение быстро (экспоненциально по времени) деградирует и становится неотличимым от нуля. В модели распада этот факт используется для автоматического сброса счетчика: хотя значение счетчика $s$ будет всё время возрастать с приходом событий, через некоторое время после прекращения потока событий величину $v=alpha^{s-t_{now}}$ можно будет считать равной нулю, не меняя явно значения счетчика. Время $T_{vanish}$, за которое любое накопленное ранее значение распадается до условного нуля, зависит от параметра $tau$ и требуемой точности. Оно выражается как $T_{vanish}=T_{min}+sigma_{max}$, где $T_{min}$ — время распада значения, накопленного в результате единичного события. В разделе «Табличная реализация» дано точное выражение $T_{min}$, но здесь достаточно иметь в виду следующий факт: $T_{vanish}=O(taulntau)$ при фиксированной точности.

Отсюда следует оценка сверху на размер хранилища счетчиков при учете множества потоков для случая, когда информация вообще не будет теряться — достаточно иметь $T_{vanish}cdot r_{max}$ ячеек. Есть множество применений задачи поиска тяжелых элементов, где не требуется больших значений $tau$, и всё хранилище помещается оперативную память или даже в кэш процессора L3 или L2. В этом случае обеспечивается малое время доступа к хранилищу, так что задача становится выполнимой при высоких значениях интенсивности входного потока.

Для реализации хранилища годится хэш-таблица, где ключом является тип события. При этом пустыми считаются ячейки, у которых значение счетчика $s$ удовлетворяет условию $s-t_{now} le T_{min}$.

Численная реализация Decay-based count

Операция обновления значения

Введем следующее обозначение:

$rho_tau(x)=tauln(1+e^{x/tau})=log_{alpha}(1+alpha^x).$

Тогда операция обновления выражается следующим образом:

$s'=t_{now} + rho_tau(s-t_{now}).$

Таким образом, задача сводится к эффективному вычислению приближения функции $rho_tau$. Время удобно представлять целым числом, например, измерять его в тактах процессора, так что требуется построить целочисленное отображение ${R:mathbb{Z}tomathbb{Z}}$, такое, что:

$R_tau(T) approx rho_tau(T)quadmbox{для }Tinmathbb{Z}.$

Для данной задачи точность важна не относительная, а абсолютная, поскольку со значениями времени используются в основном аддитивные операции. Очевидно, что из-за целочисленности представления времени погрешность меньше 0.5 такта недостижима.
Кроме того, операция измерения текущего времени, как правило, дает некоторую погрешность. Например, если есть способ измерения времени с точностью в 10 тактов, то достаточно потребовать, чтобы $R_tau$ давало приближение примерно такой же точности: $left|R_tau(T) - rho_tau(T)right| le 10.$

Можно предложить несколько разных способов вычисления $R_tau$ разной сложности и степени эффективности.

Вычисление $R_tau$: FPU

Проще всего использовать арифметику с плавающей точкой и непосредственно вычислять $rho_tau$ по определению. Время выполнения этой операции составляет около 100 тактов процессора, что довольно много по сравнению предлагаемым ниже методом.

Вычисление $R_tau$: табличная реализация

Идея табличной реализации состоит в том, чтобы сохранить предвычисленные значения функции в таблице.

Во-первых, используя тождество

$rho_tau(-x)=-x + rho_tau(x),$

достаточно строить $R_tau(T)$ только для $Tle0$.

Во-вторых, поскольку

$rho_tau(x)to 0 mbox{ при } xto-infty,$

существует $T_{min}>0$, такое что $R_tau(T)=0$ при $Tle-T_{min}$. Где $T_{min}$ можно найти из следующих соображений:

$T_{min}=lceil t_{min}rceil,quad rho_tau(t_{min})=1/2,$

откуда
$T_{min}=lceil-log_alpha(alpha^{1/2}-1)rceil=lceil-tauln(e^{1/{2tau}}-1)rceil.$

Таким образом, достаточно определить $R_tau(T)$ для ${T_{min}<Tle0}$.

График функции $rho_tau(x)$ представлен на рис. 3. Особенность этой функции такова, что с изменением параметра $tau$ будет происходить одинаковое масштабирование по обеим осям.

Измерение интенсивности входящего потока событий в модели распада - 150

Рисунок 3: График функции $rho_tau(x)$

Очевидная реализация $R_tau$ состоит в построении таблицы из $T_{min}$ ячеек, где будут храниться предвычисленные значения. Поскольку все значения функции на данном интервале находятся в промежутке между 0 и $rho_tau(0)=tauln2$, итоговый размер таблицы составляет $T_{min}log_2(tauln2)$ бит.

Алгоритм обновления значения выглядит следующим образом:

$begin{align} t_{now}& leftarrow getTime()\ delta & leftarrow min{|s-t_{now}|, T_{min}}\ delta' &leftarrow R(-delta)\ s' &leftarrow delta' + max{s, t_{now}} end{align}$

Абсолютная точность этого метода составляет 1/2, поскольку он дает наилучшее целочисленное приближение вещественнозначной функции.

Результаты измерения эффективности

Сравнивались между собой следующие три реализации экспоненциального скользящего среднего:
1. наивная реализация EMA;
2. модель распада через FPU (то есть с вызовом функций exp() и log() математической библиотеки);
3. модель распада табличным методом.

Исходный код теста на си: pastebin.com/wiiEe6MP.

Время выполнения одного вызова функции update() при $tau=100000$ (в этом случае таблица для вычисления $R_tau$ помещается в кэш L1) в реализациях 1, 2 и 3 составляет 125, 100, 11 тактов процессора, соответственно.

Использование экспоненциального скользящего среднего — удобный способ подсчёта событий и оценки интенсивности. Однако данная операция вычислительно затратна, что сильно ограничивает возможности её применения. Наша реализация алгоритма на основе модели распада, во-первых, красива, а во-вторых, более эффективна, нежели наивная реализация вычисления ЕМА. Эффективность обеспечивается за счет двух факторов: табличное вычисление трансцендентной функции и более экономное по памяти представление счетчика.

Благодарность

Данная публикация подготовлена нами в пробном режиме в рамках проекта по освещению механизмов работы сети фильтрации Qrator. Спасибо Антону Орлову, Артему Гавриченкову и Евгению Наградову за наводящие вопросы и предложения.

Автор: Shapelez

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js