Наткнулась на эту задачу совершенно случайно. У меня знакомая через год после окончания магистратуры снова решила учиться и начала готовиться к поступлению. А значит что-то нужно просто повторить и вспомнить, ну и разобраться с чем-то новым. Вот сидела она над какой-то задачей, я проходила мимо. Задача показалась весьма простой (школьного уровня), но надо немного подумать.
Итак, рассматриваемая здесь задача звучит так: даны угол и точка внутри него. Через эту точку провести отрезки, имеющие концы на сторонах угла, так, чтобы полученный треугольник имел наименьший периметр.
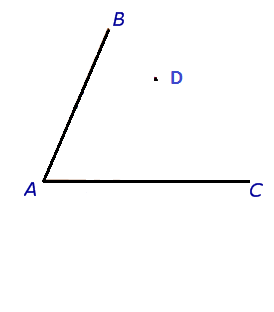
Задачка является частью доказательства задачи Фаньяно.
, вершины 
, 
и 
которых лежат на сторонах 
, 
и 
остроугольного треугольника 
соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника 
.
Первые мысли, которые приходят в голову, это, наверное, построить перпендикуляры (как кратчайшее расстояние до сторон). Отображаем точку 
симметрично относительно 
и 
(получаем точки 
и 
).
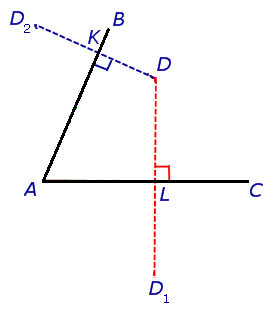
У некоторых сразу же может возникнуть искушение соединить точки пересечения перпендикуляров и сторон угла 
. После чего появляется ложное впечатления «я сделяль», и кажется, что 
— это тот самый треугольник.
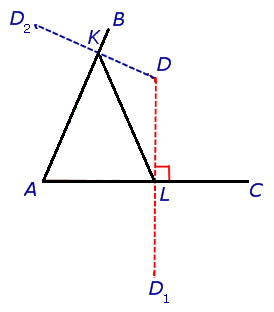
Всё не так. Тот факт, что две стороны треугольника — кратчайшие (перпендикуляры до прямой), еще не делает периметр треугольника минимальным.
На самом деле поиск треугольника с наименьшим периметром использует утверждение: кратчайшее расстояние между двумя точками – прямая. Дополнительные построения должны привести к тому, чтобы все длины сторон искомого треугольника оказались на прямой. Соединяем точки 
и 
. Точки пересечения прямой 
со сторонами угла и есть оставшиеся искомые вершины треугольника.
и 
являются медианами и высотами(точка 
симметрично отображена относительно сторон угла) треугольников 
и 
соответственно, значит треугольники 
и 
— равнобедренные. Видно, что периметр треугольника 
равен длине отрезка 
. Треугольник с меньшим периметром найден.
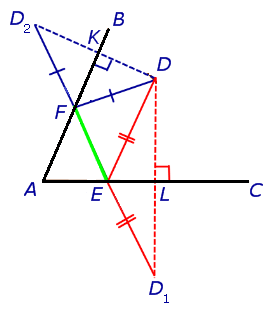
Возьмем какие-нибудь другие точки(
и 
) на сторонах угла.
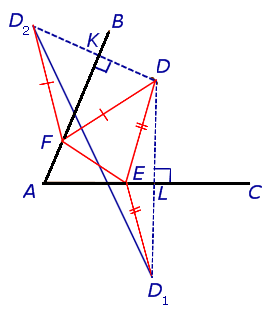
Периметр этого треугольника 
оказывается больше, чем длина отрезка 
.
Вот и все. Удачи всем поступающим!
Автор: AnROm
