
Изучая иностранную литературу, на днях наткнулся на работы [1, 2] профессора Мичиганского университета Дивакара Вишваната (Divakar Viswanath) об итерационном алгоритме вычисления периодических орбит динамических систем, основанном на методе Линдштедта-Пуанкаре (ЛП) (для ознакомления с ним рекомендую книгу [3, с. 408-411]). Преимуществом данного метода является то, что он не требует численного интегрирования дифференциального уравнения, поэтому может быть применён к построению и неустойчивых циклов.
На сегодняшний день в математике одно из популярных направлений исследований — это теория динамического хаоса. Самым известным объектом здесь является система Лоренца, введённая в 60-е годы 20-ого века. Отмечу, что с того времени появилось много нелинейных математических моделей, где имеет место хаотическое поведение решений, в различных областях науки. Несколько лет назад получили популярность хаотические системы без положений равновесия, применяемые для шифрования сигналов (см., например, [4]). Тем, кто только начинает заниматься теорией хаоса, советую посмотреть математический фильм ХАОС, состоящий из девяти глав.
Уорвик Такер (Warwick Tucker) в работе [5] доказал существование периодических решений в аттракторе Лоренца, но убедительных доказательств найденных циклов в численных экспериментах авторов различных статей мне не удавалось найти.
Пусть x(t), y(t) и z(t) — фазовые координаты системы Лоренца. В 2004 году Вишванатом в работе [2] были найдены три цикла ЛП-методом. Он привёл значения начальных условий и периода:

где T — период.
На мой взгляд, это значительный прорыв в исследовании аттрактора Лоренца.
Может возникнуть вопрос — зачем 99 знаков в дробной части чисел? Дело в том, что периодические орбиты являются неустойчивыми (и эти числа, скорее всего, являются иррациональными), и чтобы их построить численными методами на периоде с приемлемой точностью, нужно располагать большим количеством знаков после запятой.
Я решил проверить и построить циклы Вишваната в программе, приведённой в топике [6] (численная схема также описана в работе [7]). Для этого была взята точность 1e-110 по степенному ряду, количество бит под мантиссу вещественного числа — 390 (машинный эпсилон при этом равен 7.93107e-118), проход по времени — только вперёд. Осуществлялась проверка следующих равенств:
x(0) = x(T),
y(0) = y(T),
z(0) = z(T).
Для первого цикла совпали все знаки в дробной части у всех координат, кроме последнего знака для y(T) (у меня там получилась цифра 6), для второго — 80 знаков, для третьего — 38 знаков.
Далее приведены рисунки циклов Вишваната.
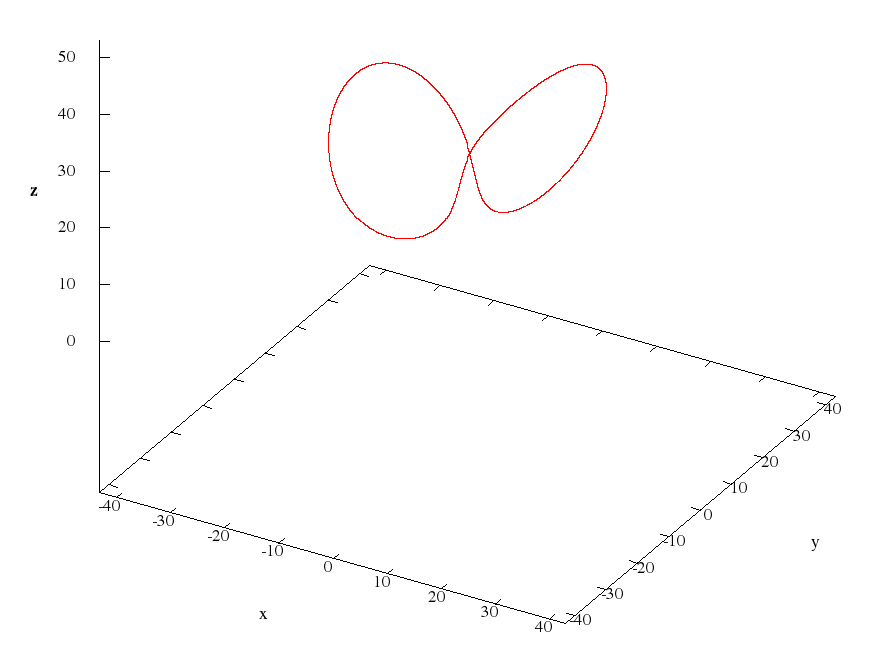
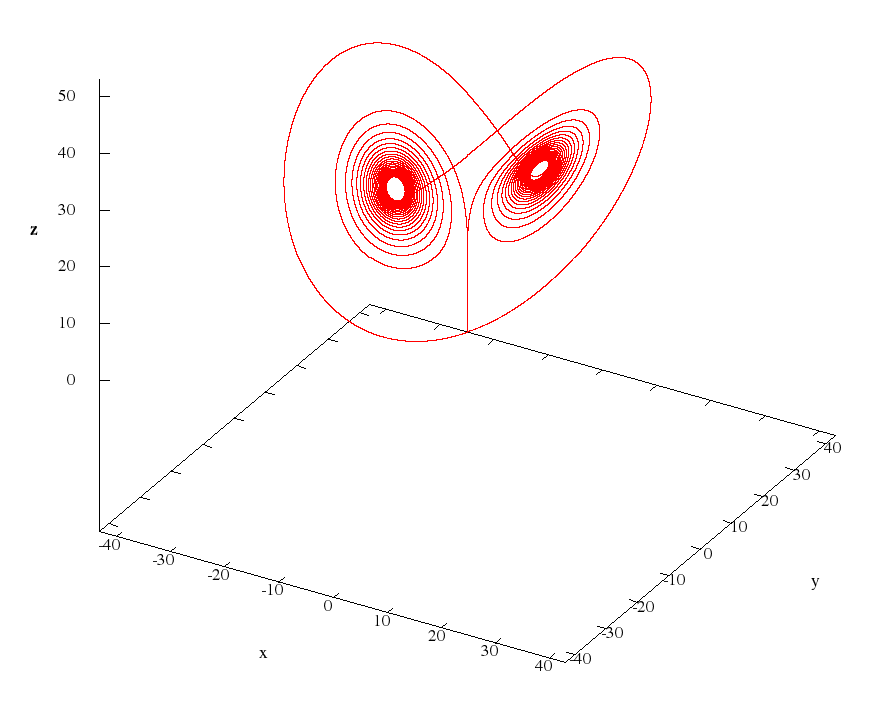
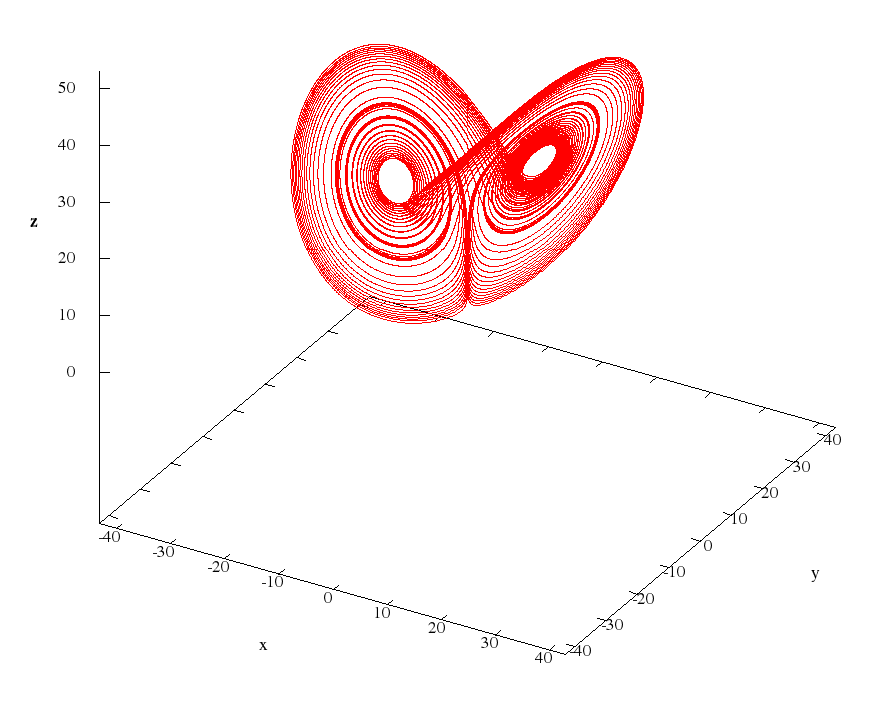
И анимация, загруженная на YouTube.
Для второго рисунка меня заинтересовало, насколько близко траектория системы проходит к началу координат O(0;0;0). В численном эксперименте найдена точка с координатами
![]()
Поскольку базовым методом для численной схемы является метод степенный рядов, для третьего цикла определена максимальная степень аппроксимирующего полинома на переменных шагах интегрирования, где решение раскладывается в ряды, — 78, приближенное максимальное значение шага интегрирования при этом = 0.0120621. Так как значение T здесь достаточно велико, время вычислений на моём компьютере составило примерно 6.2 мин.
Литература
1. Viswanath D. The Lindstedt-Poincare Technique as an Algorithm for Computing Periodic Orbits // SIAM Review. — 2001. — Vol. 43, Iss. 3, pp. 478-495.
2. Viswanath D. The Fractal Property of the Lorenz Attractor // Physica D: Nonlinear Phenomena. — 2004. — Vol. 190, Iss. 1-2, pp. 115-128.
3. Федорюк М.В. Обыкновенные дифференциальные уравнения. — М.: Наука, 1985. — 448 с.
4. Wang Z., Akgul A., Pham V.-T., Jafari S. Chaos-Based Application of a Novel No-Equilibrium Chaotic System with Coexisting Attractors // Nonlinear Dynamics. — 2017, pp. 1-11.
5. Tucker W. A Rigorous ODE Solver and Smale's 14th Problem // Foundations of Computational Mathematics. — 2002. — Vol. 2, Iss. 1, pp. 53-117.
6. Пчелинцев А. Динамическая система Лоренца и вычислительный эксперимент, 2014. Хабрахабр. https://habrahabr.ru/post/229959/
7. Пчелинцев А.Н. Численное и физическое моделирование динамики системы Лоренца // Сибирский журнал вычислительной математики. — 2014. — Т. 17, №2. — С. 191-201.
Автор: pchelintsev_an

