На некотором сайте, в некотором форуме, добрый молодец по прозвищу SciFi озадачил коллектив свой историей.
Нашел он в руководящих технических материалах иноземной фирмы Texis Instrument [FSK Modulation and Demodulation With the MSP430 Microcontroller] требуемый ему цифровой фильтр. Но иноземцы шибко хитры оказались, и в исходном коде привели следующее:
**************************************************
* Running this filter takes 113 cycles
**************************************************
;*****************************************************
; New simpler filter at following specification
; Freq_Stop: 2.5KHz, Attenuation_Stop: 40dB
; Freq_Pass: 1.4KHz, Attenuation_Pass: 1dB
; Order of filter = 5
;*****************************************************
filters:
bis #INTERRUPT_TOGGLE,global_status
mov #WDF_PARMS,mem_ptr
.word 4f16h
.word 0000h
.word 498fh
.word 0000h
.word 4f17h
.word 0008h
.word 8607h
.word 4708h
.word 1108h
.word 4806h
.word 1108h
.word 1108h
.word 1108h
.word 1108h
.word 1108h
.
.
.
Зашифровали демоны! Но добрый молодец SciFi, тоже не промах оказался. Одолел их хитрости и перевел их тайнопись на язык С:
signed short filter(signed short x)
{
static signed short fltmem[5];
signed short r6, r7, r9;
r7 = fltmem[4] - fltmem[0];
fltmem[0] = x;
r6 = (r7 >> 1) - (r7 >> 6) - fltmem[4];
fltmem[4] = fltmem[3];
fltmem[3] = r6;
r6 -= r7;
r7 = fltmem[2] - x;
r9 = (r7 >> 3) - (r7 >> 6) + fltmem[2];
r7 -= r9;
fltmem[2] = fltmem[1];
fltmem[1] = r7;
return (r6 - r9)>>1;
}
Как выяснилось, демоны шифровались дважды. Данный код получен явно с использованием компилятора, так использовать относительную адресацию может только компилятор. Но сам по себе код заслуживает интереса и уважения. Как видно, он не содержит операций умножения и может эффективно выполнятся даже на самых простых процессорах. У доброго молодца SciFi, и у всех остальных, возник вопрос: “Что это за фильтр?”.
Восстановить структурную схему фильтра по такому коду, если и возможно, то весьма трудоемко. Поэтому мы пойдем другим путем. Вывод о типе и параметрах фильтра будем делать по амплитудно-частотной характеристике (АЧХ). Как ее получить? Да как два байта переслать.
Сразу отметим, что данный фильтр является фильтром с бесконечной импульсной характеристикой. Это угадывается в исходном коде, состояние фильтра хранится в массиве static signed short fltmem[5];
Снимем 60 отсчетов импульсной характеристики фильтра, то есть, реакцию фильтра на единичный импульс. Но в условиях целочисленной арифметики, чтобы получить конечный результат с наилучшей точностью, будем подавать на вход фильтра значение не 1, а 10000. Точнее, надо подавать максимально возможное число, не вызывающие переполнения.
Тестовый код для снятия импульсной характеристики:
printf("%drn", filter(10000));
for(int i=1;i<100;i++)
{
printf("%drn", filter(0));
}Полученный результат, с помощью копипастинга, обработаем в математическом пакете MathCad.
Построим график импульсной характеристики. На интервале 0-20 отсчетов он выглядит так:
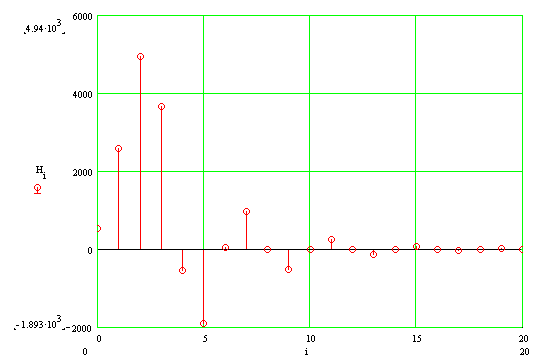
И на интервале 20-60 отсчетов он выглядит так:
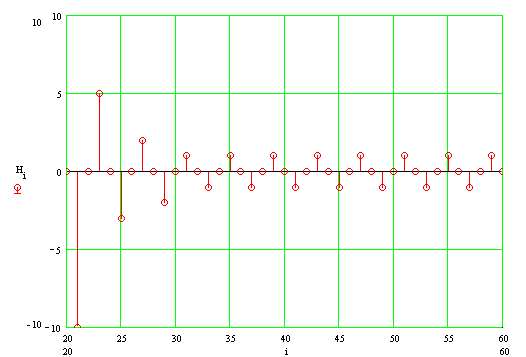
Из анализа импульсной характеристики видно, что фильтр не лишен недостатков. Импульсная характеристика содержит незатухающие колебания, амплитудой одна дискрета. В теории синтеза фильтров с бесконечной характеристикой [Гольденберг Л. М. и др. Цифровая обработка сигналов. М.: Радио и связь, 1985] такие колебания принято называть предельными циклами, которые возникают из-за ошибки округления целых чисел.
Комплексный коэффициент передачи исследуемого фильтра можно определить как преобразование Фурье от импульсной характеристики. Только в случае дискретной импульсной характеристики интегрирование по временой оси можно заменить сложением по всем ненулевым отсчетам. В нашем случае коомплексный коэффициент передачи случае определится выражением:
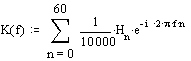
Где H – массив отсчетов импульсной характеристики;
f – частота, нормированная относительно частоты дискретизации;
Построим график модуля комплексного коэффициента передачи, амплидудно-частотную характеристику, в логарифмическом масштабе (ЛАЧХ). Здесь и далее, при построении графиков, используется частота, нормированная относительно частоты дискретизации.
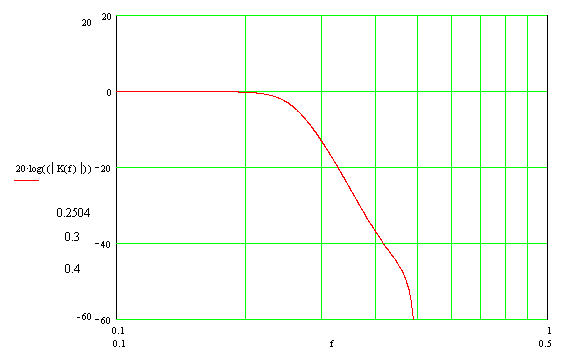
С помощью встроенных средств математического пакета определим ключевые точки АЧХ:
- Частота среза фильтра по уровню -3дБ – 0.25
- Коэффициент передачи на частоте 0.3 — -13.266дБ
- Коэффициент передачи на частоте 0.4 — -37.013дБ
Соответственно, наклон характеристики вне полосы пропускания составляет:
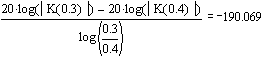Дб/декада
Для полноты картины приведем фазо-частотную характеристику (ФЧХ):
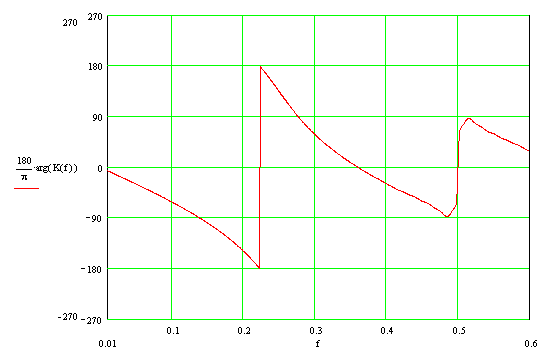
Фазовый сдвиг на частоте 0.48 составляет (180+180+87)=447 градусов. Разрыв фазы на графике может вызвать недоумение, если забыть о неоднозначности арктангенса.
Так же, для полноты картины, приведем групповое время запаздывания (ГВЗ).
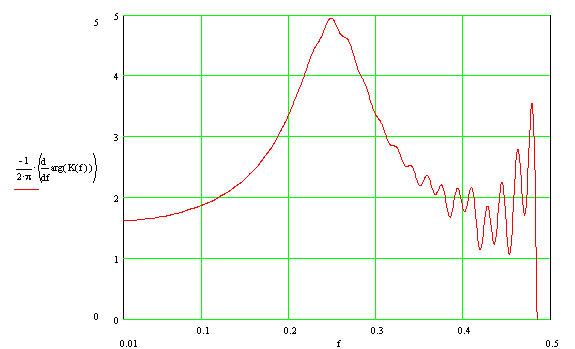
Теперь, глубоко задумавшись, можно ответить на вопрос “Что это за фильтр?”.
Порядок фильтра. Из анализа логарифмической амплитудно-частотной характеристики можно предположить, что данный фильтр является звеном 10 порядка, наклон характеристики вне полосы пропускания составляет около 20*10=200 дБ/декаду. Но из анализа фазовой характеристики видно, что фазовый сдвиг стремится к 90*5=450 градусам. Тут у неискушенного “угадывателя фильтров” невольно возникают мысли о неминимально-фазовости данного звена. Но не стоит забывать, что “аналоговая” частота отображается в “цифровую” через тангенс и, следовательно, законы аналогового мира (20дБ/декаду и т.п.) работают только на частотах много меньше частоты дискретизации. В нашем же случае, мы рассматриваем ЛАЧХ на участке близком к половине частоты дискретизации, и законы аналогового мира не работают.
Таким образом, по виду фазовой характеристики можно сделать вывод, что данное звено является звеном 5 порядка.
Тип фильтра. Принимая во внимания вид ЛАЧХ (в полосе пропускания ЛАЧХ максимально плоская) и вид графика ГВЗ (экстремум в окрестности частоты среза) можно предположить, что данное звено является фильтром Баттерворта. Для подтверждения нашего предположения построим ЛАЧХ, ФЧХ и ГВЗ идеального цифрового фильтра Баттерворта с частотой среза 0.25 синтезированного методом билинейного преобразования [Википедия].
На графиках красной сплошной линией обозначены величины соответствующие исследуемому фильтру, синей пунктирной линией — идеальному цифровому фильтру Баттерворта синтезированного методом билинейного преобразования
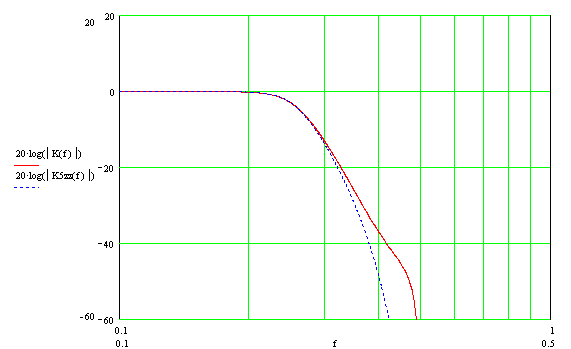
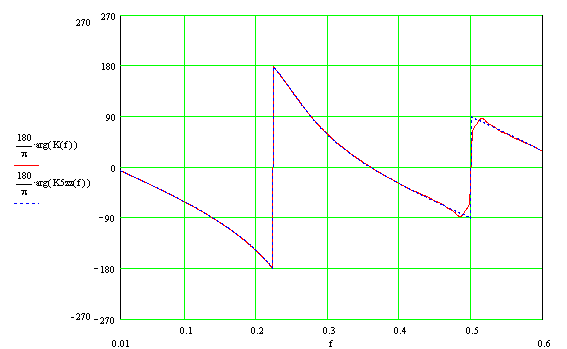
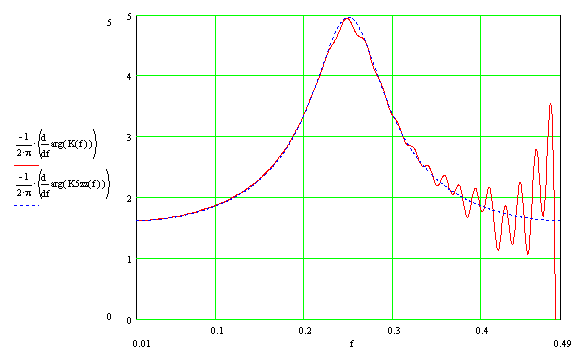
Как видно из графиков, практически полное совпадение параметров исследуемого фильтра с параметрами идеального цифрового фильтра Баттерворта синтезированного методом билинейного преобразования.
Заключение.
В данной работе мы исследовали замечательную реализацию цифрового фильтра Баттерворта 5-порядка. Данная реализация фильтра, не смотря на свои недостатки в виде предельного цикла, заслуживает большого уважения. Инженерам фирмы Texis Instrument удалось воплотить достаточно сложный алгоритм фильтра 5 порядка в целых числах, не используя операций умножения и деления, при этом обеспечить приемлемую устойчивость и соответствие характеристик фильтра прототипу.
Ваш покорный слуга, искренне надеется, что использованный в данной работе метод анализа кода цифровых фильтров будет интересен и полезен читателю.
Автор: IBAH_II
