Вручную выписывать коэффициенты СЛАУ и вводить их в программу — не самый эффективный способ программирования метода конечных разностей, потому что для каждой новой вариации постановки задачи потребуется писать новую программу. Логичнее разработать общий солвер для более широкого класса задач, что упростит программирование и тестирование. Тестирование алгоритмов МКР затруднено, так как точное решение неизвестно, но общий солвер можно протестировать на задачах с заданным точным решением.
Автором разработан солвер Joker FDM для решения 1- и 2-мерных задач сопряжения для эллиптических уравнений методом конечных разностей.
Постановка задачи
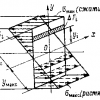
Рассматривается прямоугольная область. Горизонтальная сторона прямоугольника разделяется на 
промежутков, вертикальная — на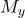 
промежутков. Таким образом, весь прямоугольник разделяется на 
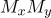прямоугольных подобластей.
В каждой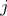 
-й подобласти, 
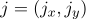, задается система дифференциальных уравнений реакции-диффузии
с граничными условиями Дирихле, Неймана или Робина и условиями сопряжения типа неидеального контакта либо идеального контакта.
Подробную постановку задачи см. в GitHub Wiki, для просмотра формул установите расширение для Chrome.
Солвер применялся автором для вычисления решения диффузионной модели сложного теплообмена (нелинейная система двух уравнений).
Не во всех конечноэлементных решателях есть функция решения задач сопряжения со скачком решения на границе раздела (неидеальный контакт). Отметим пакет FEniCS, в котором есть такая функция.
Описание алгоритма
В области вводится сетка: каждый x- и y-промежуток разбивается на равные части.
Применяется разностная схема 2-го порядка, описанная в книге Самарского, Андреева «Разностные методы для эллиптических уравнений».
Для линеаризации нелинейных уравнений используется метод Ньютона. Этот метод хорошо зарекомендовал себя для решения уравнений сложного теплообмена.
Формулировку и обоснование одномерной разностной схемы см. в wiki.
Описание солвера
1-мерный солвер реализован на Octave и C++, 2-мерный – только на C++.
Разностные уравнения записываются в виде суммы одномерных разностных операторов по x и y и нелинейного точечного оператора. Реализация общего алгоритма через сумму одномерных операторов позволяет не рассматривать большое количество типов узлов (внутренние, на стороне прямоугольника, в угловой точке, на границе раздела подобластей, на стороне прямоугольника и на границе раздела, в угловой точке на границах раздела). Для записи уравнений используется понятный синтаксис с перегрузкой операций.
Для решения СЛАУ применяется итерационный метод из библиотеки MTL4.
В дальнейшем планируется реализовать 3-мерный солвер аналогичным образом.
Заключение
Можно программировать метод конечных разностей по-простому: выписать разностные уравнения для конкретной задачи, ввести коэффициенты в программу и вызвать функцию решения СЛАУ.
Более продуктивно разработать общий солвер, который можно протестировать на задачах с известным решением.
Автор: grenkin
