Одним из красивейших математических результатов можно смело считать теорему Эйлера, которая впервые появилась в журнале Петербургской Академии наук в работах Леонарда Эйлера «Элементы учения о телах» и «Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями».
Теорема Эйлера. Пусть 
– число вершин выпуклого многогранника, 
– число его ребер и 
– число граней. Тогда верно равенство
Число 
называется эйлеровой характеристикой многогранника. Легко вычислить эйлерову характеристику для некоторых знакомых нам многогранников.
| Многогранник |  |
 |
 |
 |
| Тетраэдр | 4 | 6 | 4 | 2 |
| Куб | 8 | 12 | 6 | 2 |
| Октаэдр | 6 | 12 | 8 | 2 |
Доказательство теоремы Эйлера может быть найдено здесь.
Давайте воспользуемся теоремой Эйлера для установления некоторых интересных фактов. Посмотрите на изображение футбольного мяча.
Вопрос: сколько нужно взять пятиугольников, чтобы сшить мяч? Пусть 
– количество шестиугольников, а 
– количество пятиугольников. Давайте применим теорему Эйлера к нашему футбольному мячу:
где 
, 
, а 
. Формулы для количества вершин, ребер и граней легко получаются из наблюдения, что каждая вершина попадает на три грани, а по каждому ребру пересекаются только две грани. Подставив значения в формулу, вы получите ответ: 
. Переменная 
исключается из уравнения, т.е. количество шестиугольников может быть каким угодно. На следующей картинке изображен мяч, сшитый из одних только пятиугольников. Сколько их?
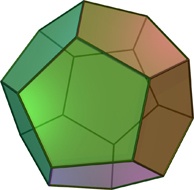
Этот многогранник называется додекаэдром и является одним из пяти правильных многогранников.
Давайте рассмотрим другой сюжет. Фуллерены — молекулярные соединения, принадлежащие классу аллотропных форм углерода и представляющие собой выпуклые замкнутые многогранники, составленные из чётного числа трёхкоординированных атомов углерода. Своим названием фуллерены обязаны инженеру и архитектору Ричарду Бакминстеру Фуллеру, чьи геодезические конструкции построены по этому принципу. Первоначально данный класс соединений был ограничен лишь структурами, включающими только пятиугольные и шестиугольные грани.
И наконец, давайте посмотрим на следующую картинку.
Ничего особенного — всего лишь купол, собранный из шестиугольников. А теперь еще раз помедитируйте над формулой Эйлера и вперед искать пятиугольники.
Этот и многие другие математические сюжеты смотрите в замечательных лекциях Алексея Савватеева или в его книге «Математика для гуманитариев».
Автор: dfedchenko
