Голуби дают людям фору в решении дилеммы Монти Холла, что могло бы позволить им успешно выступать на одноименном ток-шоу. Это закономерность может, в свою очередь, излить свет на то, почему людям так трудно она дается.
Чем примечательна эта дилемма? При кажущейся простоте, она запутывает логические цепочки наших умозаключений, заставляя людей (но не голубей), в буквальном смысле, блуждать в трех соснах, вернее — в дверях. Это свойственно представителям самых разных культурных традиций: американцы, китайцы, шведы и бразильцы совершают одинаково неверный выбор.
Когнитивный психолог Massimo Piattelli-Palmarini заметил по этому поводу: Ни одна статистическая задача даже рядом не стоит по способности дурачить всех людей и во все времена.
В этой статье мы узнаем, в чем состоит дилемма, найдем теоретическое верное решение, проверим его в R, расскажем про интеллектуальную битву людей с голубями и узнаем ее результаты.
Дилемма Монти-Холла
Так называемая дилемма Монти Холла является хорошо известной загадкой, названной так в честь первого телеведущего на американском ТВ-шоу «Предлагаю Сделку», в которой тот давал участникам на выбор три двери, за одной из которой была машина, а за двумя остальными — козлы. Приз и козлы заранее расставлялись случайным образом и далее не меняли свои местоположения. После того как участник делал свой выбор, ведущий всегда открывал одну из оставшихся двух дверей, за которой, как он знал наперед, не было приза. Затем игроку предлагалась возможность поменять свой выбор или оставить все как есть.
На самом деле существует несколько возможных стратегий Монти.
- Адский Монти: ведущий предлагает сменить, если дверь правильная.
- Ангельский Монти: ведущий предлагает сменить, если дверь неправильная.
- Ведущий выбирает одну из коз и открывает её, если игрок выбрал другую дверь.
Классикой стала стратегия непредвзятости ведущего, когда он при любом изначальном выборе игрока открывает козло-дверь и предлагает поменять свой выбор или все оставить как есть. От нее мы и будем далее отталкиваться.
Подавляющее большинство игроков, опрашиваемых и испытуемых отказывались менять свой выбор, не смотря на то, что это удваивало их шансы на выигрыш. При этом люди мыслят, что в оставшихся двух дверях шансы на выигрыш равны и менять свой выбор нет никакого смысла. Если вы думаете так же, не смущайтесь, ибо не один вы заблуждаетесь.
Когда колумнист Mаrilin vos Savant[1] опубликовала решение в журнале Parade Magazine, на нее посыпался просто шквал писем читателей, выражающих свое несогласие. Вот например такие.
Я уверен, что скоро Вы получите много писем от студентов высших школ и колледжей. Возможно, Вам следует сохранить эти адреса, они помогут Вам в последующих выпусках.
W. Robert Smith, Ph.D. / Georgia State UniversityЯ в шоке оттого, что даже после того, как Вас исправили по меньшей мере три математика, Вы все еще не видите свою ошибку.
Kent Ford / Dickinson State UniversityТы сама коза.
Glenn Calkins / Western State College
Всего — около 10 тыс. писем. Как видим троллинг процветал еще в те времена, когда для этого нужно было потратить гораздо больше времени и усилий чем сейчас, а еще оплатить почтовый конверт и почтовую марку.
Талантливейший венгерский математик Paul Erdős также попался на уловку и отказывался даже принять решение, пока не увидел своими глазами компьютерную симуляцию результатов эксперимента. Честно говоря, с трудом в это верится, но молва пошла, тем не менее.
Разоблачение
Самое лаконичное объяснение решения ДМХ (Дилеммы Монти Холла) дано в круговой диаграмме.
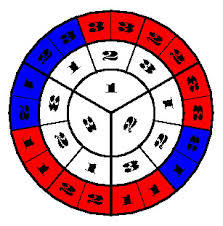
Внутренний круг показывает дверь за которой приз, средний круг указывает на первоначальный выбор участника а внешний — дверь, что откроет Монти. Последний также указывает на выигрышные расклады — они показаны красным цветом и их вдвое больше чем проигрышных синих. Простая арифметика показывает нам, что шансы выиграть при постоянном выборе равны 1/3, а смена выбора дает 2/3.
Рассмотрим теперь формальное решение задачи, на основе Теоремы Байеса об условной вероятности.
- Пусть А — событие, при котором машина за 1-й дверью.
- Пусть Б — событие, при котором Монти Холл открывает 2-ю дверь с козлом.
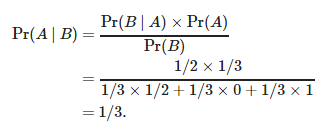
Pr(A) считается просто — 3 двери с одинаковой вероятностью выбора, значит машина за первой дверью с вероятностью 1/3. Вероятность нахождения приза в оставшихся двух одинакова, отсюда Pr(B|A)=1/2.
Рассчитать Pr(B), что в знаменателе, немного сложнее. Учитывая, что:
- Вы выбираете дверь под номером 1, а Монти показывает козла за дверью под номером 2.
- Если машина за 1-й дверью, то Монти с вероятностью 1/2 покажет дверь под номером 2.
- Если машина за 2-й дверью, то Монти всегда будет открывать дверь под номером 3, так как он никогда не показывает машину.
- Если машина за 3-й дверью, то Монти всегда будет открывать дверь под номером 2, так как он никогда не показывает машину.
Так и получается, что вероятность выигрыша равна 1/3, когда игрок не меняет дверь. Соответственно, смена двери, после демонстрации козла ведущим, равна 2/3.
А голуби что?
Немало изумленные косностью некоторых паттернов человеческого разума, исследователи Julia Schroder и Walter Hebranson задались целью проверить результаты на голубях, которые неплохо себя зарекомендовали в ряде практических теоретико-вероятностных задачах.
Пернатые и в этот раз не обманули ожиданий. После некоторой тренировки, голуби эмпирическим путем научились выбирать верную стратегию, а вот люди в том же эксперименте — нет.
Дело было так. Ученые отобрали шестерых заурядных сизых голубей и дали им на выбор три светящиеся кормушки. Следовал первоначальный выбор клювом, все три кормушки затухали и после недолгой паузы вновь начинали светится две, из которых голубь одну выбрал в начале. Компьютерная симуляция подменяла Монти Холла, убрав одну пустую кормушку, после чего испытуемое могло выбрать по-новой из оставшихся двух. Призом являлась еда — когда голубь верно угадывал кормушку, та открывалась и птица получала награду. Награда усиливала стимул и давала импульс к обучению. Затем появлялась новая тройка светящихся кормушек.
Птицы быстро научились считать свою выгоду и за 30 дней процент переключений кормушки вырос с 36.33% до 96.33%.
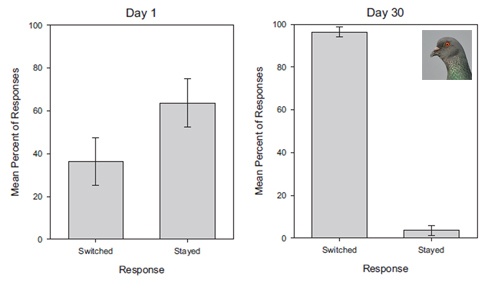
График роста голубиных показателей: на вертикальные линии над столбиками — доверительный интервал. Левый столбик показывает смену выбора а правый — тот же выбор. Некоторые птицы достигли абсолютных показателей — переключались всегда.
С людьми вышло иначе. За 30 дней эксперимента некоторый прогресс вначале наблюдался, но выявить тенденцию не удалось.
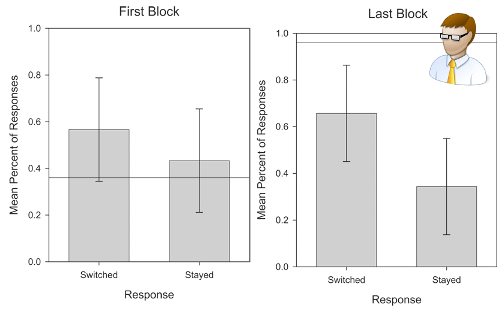
Рост надоев показателей с 56.67% до 65.67%. Границы доверительного интервала указывают на то, что выбор мог определяться случайностью.
Была проведена еще одна серия испытаний, в которых условия дилеммы Монти Холла ставились так, что выгоднее стало придерживаться изначального выбора. Целью было проверить способность найти оптимальную стратегии даже когда условия неожиданно меняются. Во втором эксперименте, местонахождение приза фиксировалось только после первоначального выбора.
Результат подтвердил тенденцию. ЦОД голубиного опять все верно рассчитал. С первый день ошибочной стратегии придерживались в 30.17% случаев, в последний же 15-й день — лишь в 4.33%. Результат юных home sapiens был едва отличим от его отсутствия: в первый день меняли выбор в 30%, в последний день — 27.67%.
Что все это значит?
В самом общем виде эти результаты можно интерпретировать следующим образом. Дело в том, как мы обучаемся и учимся оценивать вероятность событий. Чаще всего наша мысль бродит по отстроенным в годы обучения коридорам в поисках оценочной модели. Затем мы загоняем в нее данные и на выходе получаем готовый ответ. Часто берутся на вооружения всевозможные эвристические методы. В целом, это неплохо работает, но иногда случаются знатные фейлы, как в случае с ДМХ.
Альтернативой является эмпирический брутфорс: наблюдения, агрегация, вывод. Этот более трудозатратный и медленный способ принятия решений, но в данном случае именно он обеспечивает голубям выработку правильной стратегии.
Возможно ответ следует искать в серии статей про Логику Мышления. Человеческий и даже птичий несет в себе еще много загадок, поэтому вместо спекуляций, в завершение темы, лучше попробуем эмуляцию ДМХ на R. Вывод скрипта русифицирован.
5:543)$ R -f monty.r
Monty Hall Problem Simulation
"Оставить прежний выбор"
Выигрыш = 3380
Количество повторов = 10000
Наблюдаемое соотношение выигрышей = 0.338
Соотношение выигрышей в теории = 0.3333333
"Изменить выбор"
Выигрыш = 6620
Количество повторов = 10000
Наблюдаемое соотношение выигрышей = 0.662
Соотношение выигрышей в теории = 0.6666667>
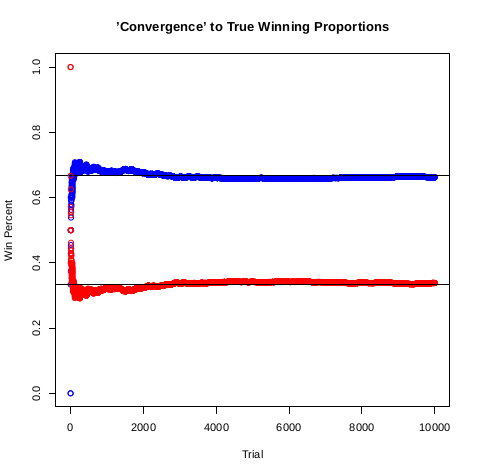
> ## Plot 'convergence' to true winning proportions
> ## Blue is switching doors, red is staying
> plot.new()
> plot(cumsum(changewin) / c(1:N), main = "'Convergence' to True Winning Proportions",
+ xlab = "Trial", ylab = "Win Percent", ylim = c(0, 1), col = "blue")
> abline(h = 2/3)
> points(cumsum(staywin) / c(1:N), type = "p", col = "red")
> abline(h = 1/3)График асимптотической сходимости к вероятностям 1/3 и 2/3.
Использованные материалы
- Are Birds Smarter Than Mathematicians? Pigeons (Columba livia) Perform Optimally on a Version of the Monty Hall Dilemma
- Pigeons Beat Humans at Solving 'Monty Hall' Problem
- Pigeons outperform humans at the Monty Hall Dilemma
- Monty Hall Problem: Intuitive and Mathematical Solutions
- ↑Автор колонки Ask Merilin, обладатель рекорда Гиннеса за самый высокий IQ.
Автор: temujin
