Нахождение экстремума (минимума или максимума) целевой функции является важной задачей в математике и её приложениях (в частности, в машинном обучении есть задача curve-fitting). Наверняка каждый слышал о методе наискорейшего спуска (МНС) и методе Ньютона (МН). К сожалению, эти методы имеют ряд существенных недостатков, в частности — метод наискорейшего спуска может очень долго сходиться в конце оптимизации, а метод Ньютона требует вычисления вторых производных, для чего требуется очень много вычислений.
Для устранения недостатков, как это часто бывает, нужно глубже погрузиться в предметную область и добавить ограничения на входные данные. В частности: МНС и МН имеют дело с произвольными функциями. В статистике и машинном обучении часто приходится иметь дело с методом наименьших квадратов(МНК). Этот метод минимизирует сумму квадрата ошибок, т.е. целевая функция представляется в виде:

Алгоритм Левенберга — Марквардта используется для решения нелинейного метода наименьших квадратов. Статья содержит:
- объяснение алгоритма
- объяснение методов: наискорейшего спуска, Ньтона, Гаусса-Ньютона
- приведена реализация на Python с исходниками на github
- сравнение методов
В коде использованы дополнительные библиотеки, такие как numpy, matplotlib. Если у вас их нет — очень рекомендую установить их из пакета Anaconda for Python
Зависимости
Алгоритм Левенберга — Марквардта опирается на методы, приведённые в блок-схеме
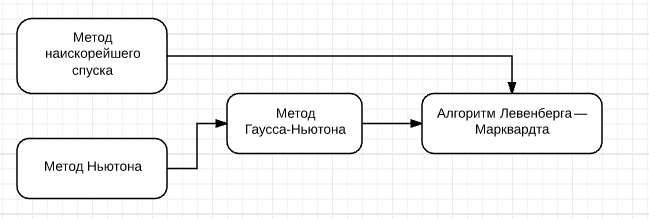
Поэтому, сначала, необходимо изучить их. Этим и займёмся
Определения
— наша целевая функция. Мы будем минимизировать
. В этом случае,
является функцией потерь
— градиент функции
в точке
—
, при котором
является локальным минимумом, т.е. если существует проколотая окрестность
, такая что
— глобальный минимум, если
, т.е.
не имеет значений меньших, чем
— матрица Якоби для функции
в точке
. Т.е. это таблица всех частных производных первого порядка. По сути, это аналог градиента для
, так как в этом случае мы имеем дело с отображением из
-мерного вектора в
-мерный, поэтому нельзя просто посчитать первые производные по одному измерению, как это происходит в градиенте. Подробнее
— матрица Гессе (матрица вторых производных). Необходима для квадратичной аппроксимации
Выбор функции
В математической оптимизации есть функции, на которых тестируются новые методы. Одна из таких функция — Функция Розенброка. В случае функции двух переменных она определяется как

Я принял 

Будем рассматривать поведение функции на интервале
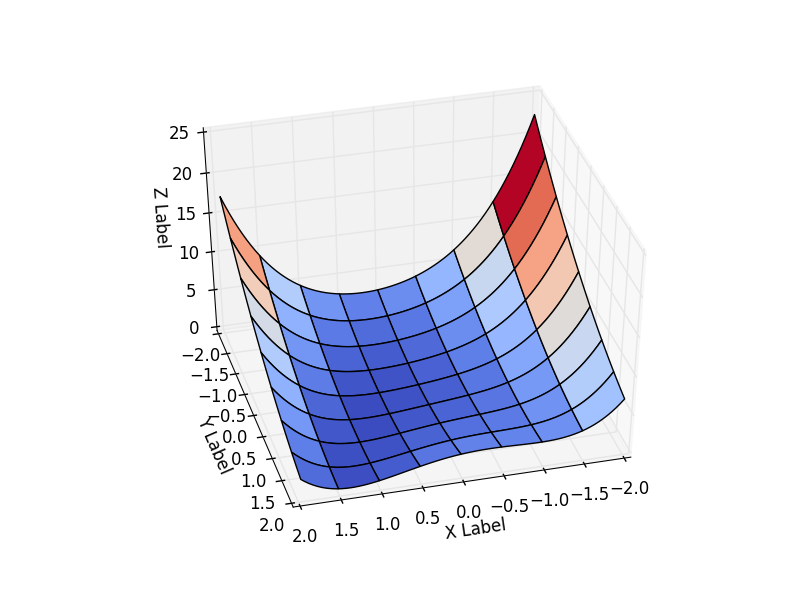
Эта функция определена неотрицательно, имеет минимум 
В коде проще инкапсулировать все данные о функции в один класс и брать класс той функции, которая потребуется. Результат зависит от начальной точки оптимизации. Выберем её как 
functions.py
class Rosenbrock:
initialPoint = (-2, -2)
camera = (41, 75)
interval = [(-2, 2), (-2, 2)]
"""
Целевая функция
"""
@staticmethod
def function(x):
return 0.5*(1-x[0])**2 + 0.5*(x[1]-x[0]**2)**2
"""
Для нелинейного МНК - возвращает вектор-функцию r
"""
@staticmethod
def function_array(x):
return np.array([1 - x[0] , x[1] - x[0] ** 2]).reshape((2,1))
@staticmethod
def gradient(x):
return np.array([-(1-x[0]) - (x[1]-x[0]**2)*2*x[0], (x[1] - x[0]**2)])
@staticmethod
def hesse(x):
return np.array(((1 -2*x[1] + 6*x[0]**2, -2*x[0]), (-2 * x[0], 1)))
@staticmethod
def jacobi(x):
return np.array([ [-1, 0], [-2*x[0], 1]])
"""
Векторизация для отрисовки поверхности
Детали: http://www.mathworks.com/help/matlab/matlab_prog/vectorization.html
"""
@staticmethod
def getZMeshGrid(X, Y):
return 0.5*(1-X)**2 + 0.5*(Y - X**2)**2
Метод наискорейшего спуска (Steepest Descent)
Сам метод крайне прост. Принимаем 
Нужно найти 






где 


Так как мы минимизируем 






Направление у нас верное, но делая шаг длиной 

Теоретически, чем меньше шаг, тем лучше. Но тогда пострадает скорость сходимости. Рекомендуемое значение
В коде это выглядит так: сначала базовый класс-оптимизатор. Передаём всё, что понадобится в дальнейшем (матрицы Гессе, Якоби, сейчас не нужны, но понадобятся для других методов)
class Optimizer:
def _init_(self, function, initialPoint, gradient=None, jacobi=None, hesse=None,
interval=None, epsilon=1e-7, function_array=None, metaclass=ABCMeta):
self.function_array = function_array
self.epsilon = epsilon
self.interval = interval
self.function = function
self.gradient = gradient
self.hesse = hesse
self.jacobi = jacobi
self.name = self.<strong>class</strong>.<strong>name</strong>.replace('Optimizer', '')
self.x = initialPoint
self.y = self.function(initialPoint)
"Возвращает следующую координату по ходу оптимизационного процесса"
@abstractmethod
def next_point(self):
pass
"""
Движемся к следующей точке
"""
def move_next(self, nextX):
nextY = self.function(nextX)
self.y = nextY
self.x = nextX
return self.x, self.y
Код самого оптимизатора:
class SteepestDescentOptimizer(Optimizer):
...
def next_point(self):
nextX = self.x - self.learningRate * self.gradient(self.x)
return self.move_next(nextX)
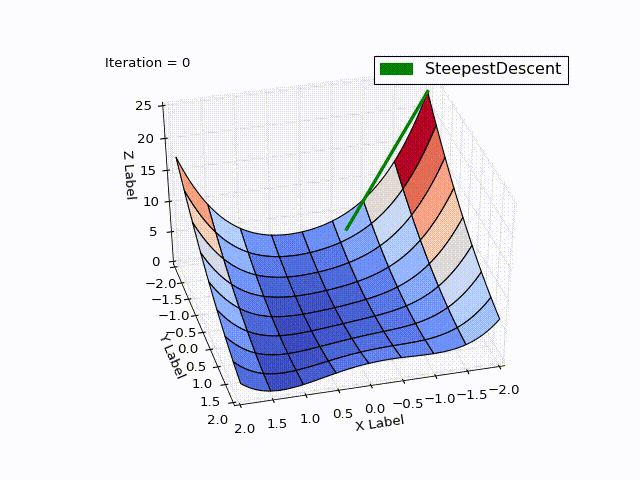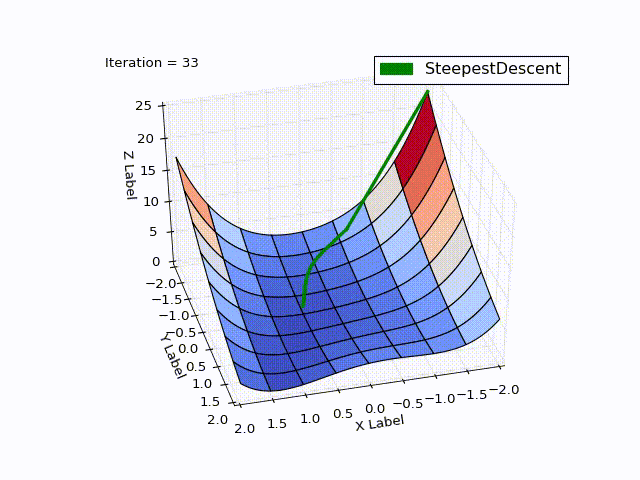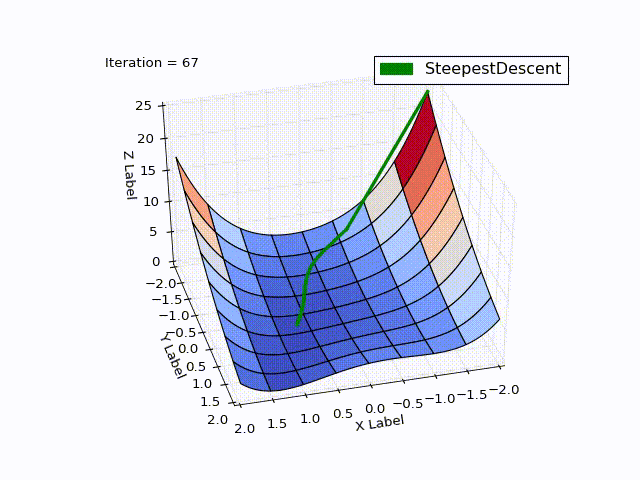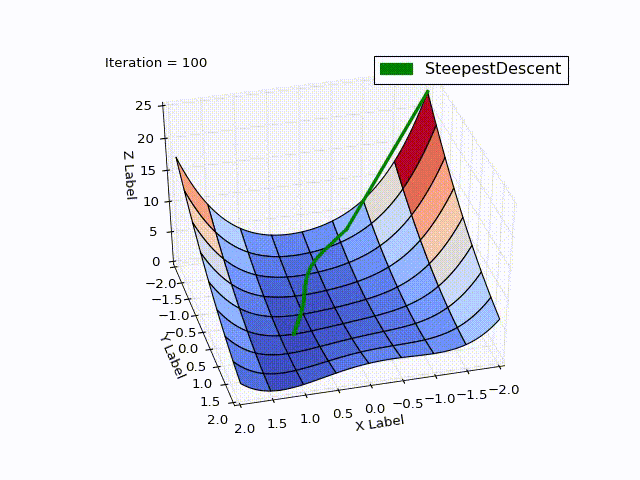
Результат оптимизации:
| Итерация | X | Y | Z |
|---|---|---|---|
| 25 | 0.383 | -0.409 | 0.334 |
| 75 | 0.693 | 0.32 | 0.058 |
| 532 | 0.996 | 0.990 |  |
Бросается в глаза: как быстро шла оптимизация в 0-25 итерациях, в 25-75 уже медленне, а в конце потребовалось 457 итераций, чтобы приблизиться к нулю вплотную. Такое поведение очень свойственно для МНС: очень хорошая скорость сходимости вначале, плохая в конце.
Метод Ньютона
Сам Метод Ньютона ищет корень уравнения, т.е. такой 

А есть ещё Метод Ньютона для оптимизации. Когда говорят о МН в контексте оптимизации — имеют в виду его. Я сам, учась в институте, спутал по глупости эти методы и не мог понять фразу «Метод Ньютона имеет недостаток — необходимость считать вторые производные».
Рассмотрим для
Принимаем 
Разлагаем 

Несложно показать, что если 



Продифференцируем обе части по 







В многомерном случае первая производная заменяется на градиент, вторая — на матрицу Гессе. Делить матрицы нельзя, вместо этого умножают на обратную (соблюдая сторону, т.к. коммутативность отсутствует):

Аналогично одномерному случаю — нужно проверить, правильно ли мы идём? Если матрица Гессе положительно определена, значит направление верное, иначе используем МНС.
В коде:
def is_pos_def(x):
return np.all(np.linalg.eigvals(x) > 0)
class NewtonOptimizer(Optimizer):
def next_point(self):
hesse = self.hesse(self.x)
# Если H - положительно определённая - Ок, иначе мы идём не в том направлении, используем МНС
if is_pos_def(hesse):
hesseInverse = np.linalg.inv(hesse)
nextX = self.x - self.learningRate * np.dot(hesseInverse, self.gradient(self.x))
else:
nextX = self.x - self.learningRate * self.gradient(self.x)
return self.move_next(nextX)
Результат:
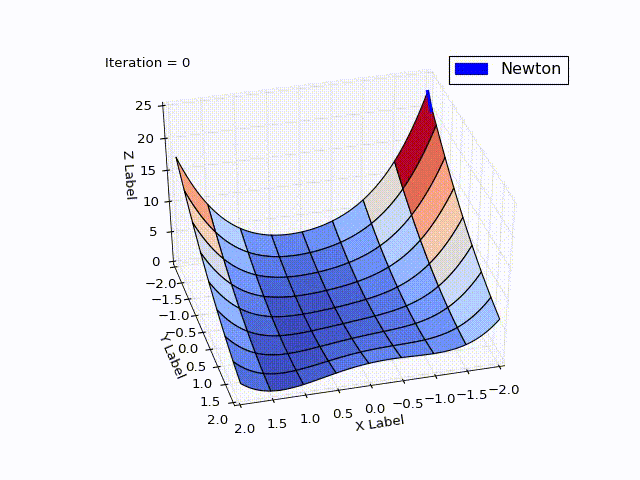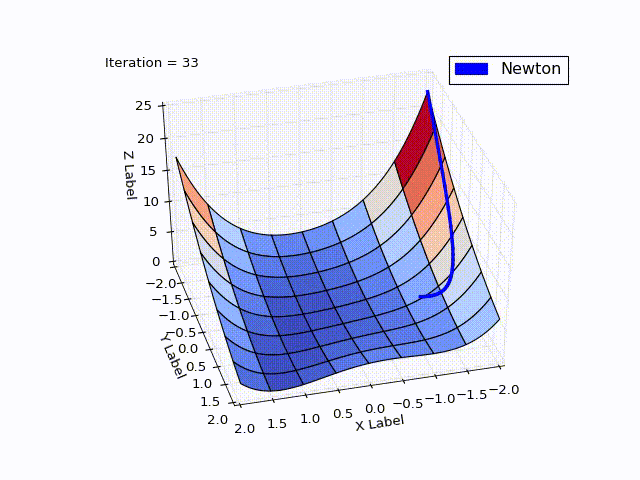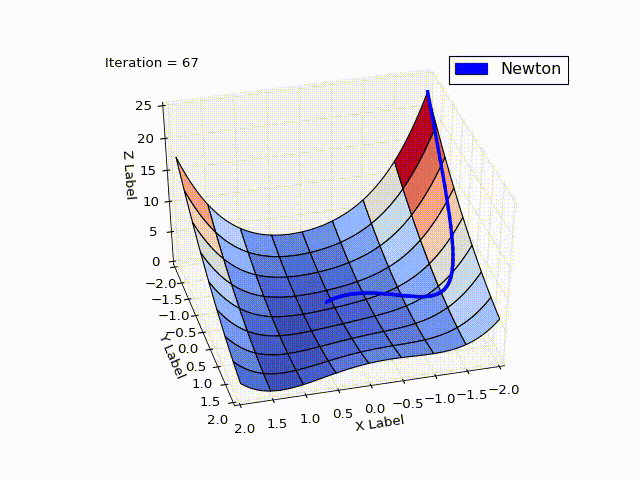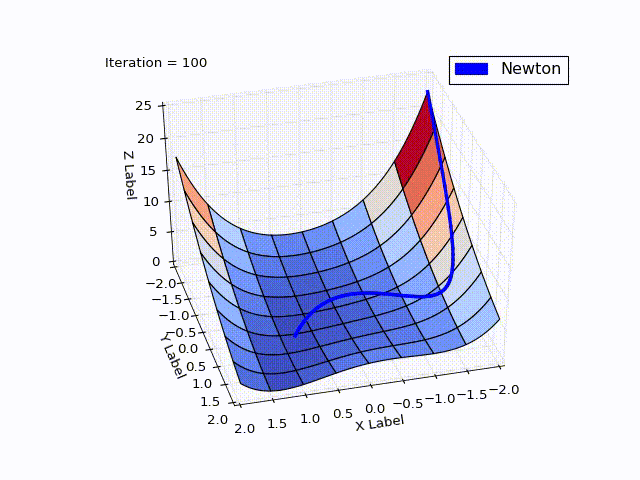
| Итерация | X | Y | Z |
|---|---|---|---|
| 25 | -1.49 | 0.63 | 4.36 |
| 75 | 0.31 | -0.04 | 0.244 |
| 179 | 0.995 | -0.991 |  |
Сравните с МНС. Там был очень сильный спуск до 25 итерации (практически упали с горы), но потом сходимость сильно замедлилась. В МН, напротив, мы сначала медленно спускаемся с горы, но затем движемся быстрее. У МНС ушло с 25 по 532 итерацию, чтобы дойти до нуля с 

Это частое поведение: МН обладает квадратичной скоростью сходимости, если начинать с точки, близкой к локальному экстремуму. МНС же хорошо работает далеко от экстремума.
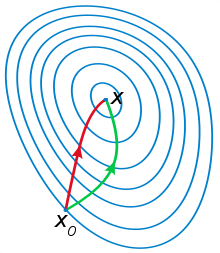
МН использует информацию кривизны, что было видно на рисунке выше (плавный спуск с горки). Ещё пример, демонстрирующий эту идею: на рисунке ниже красный вектор — это направление МНС, а зелёный — МН
[Нелинейный vs линейный] метод наименьших квадратов
В МНК у нас есть модель 




В линейном МНК у нас есть 

Для линейного МНК решение единственно. Существуют мощные методы, такие как QR декомпозиция, SVD декомпозиция, способные найти решение для линейного МНК за 1 приближённое решение матричного уравнения 
В нелинейном МНК параметр 


Здесь же приходится находить решение итеративно, причём решение зависит от выбора начальной точки.
Методы ниже имеют дело как раз с нелинейным случаем. Но, сперва, рассмотрим нелиненый МНК в контексте нашей задачи — минимизации функции

Ничего не напоминает? Это как раз форма МНК! Введём вектор-функцию

и будем подбирать 

Тогда нам нужна мера — насколько хороша наша аппроксимация. Вот она:

Я применил обратную операцию: подстроил вектор-функцию 




Напоследок, один очень важдный момент. Должно выполняться условие 
Метод Гаусса-Ньютона
Метод основан на всё той же линейной аппроксимации, только теперь имеем дело с двумя функциями:

Далее делаем то же, что и в методе Ньютона — решаем уравнение (только для 

Несложно показать, что вблизи 

Код оптимизатора:
class NewtonGaussOptimizer(Optimizer):
def next_point(self):
# Решаем (J_t * J)d_ng = -J*f
jacobi = self.jacobi(self.x)
jacobisLeft = np.dot(jacobi.T, jacobi)
jacobiLeftInverse = np.linalg.inv(jacobisLeft)
jjj = np.dot(jacobiLeftInverse, jacobi.T) # (J_t * J)^-1 * J_t
nextX = self.x - self.learningRate * np.dot(jjj, self.function_array(self.x)).reshape((-1))
return self.move_next(nextX)
Результат превысил мои ожидания. Всего за 3 итерации мы пришли в точку 
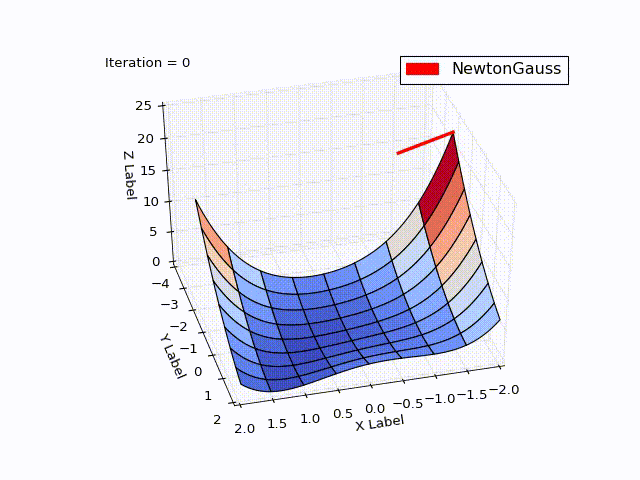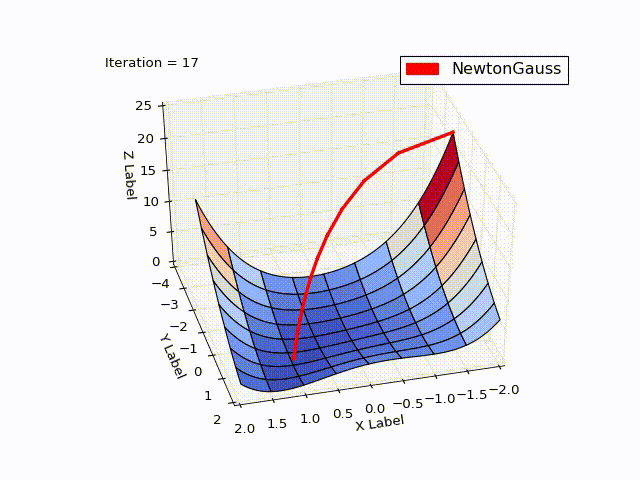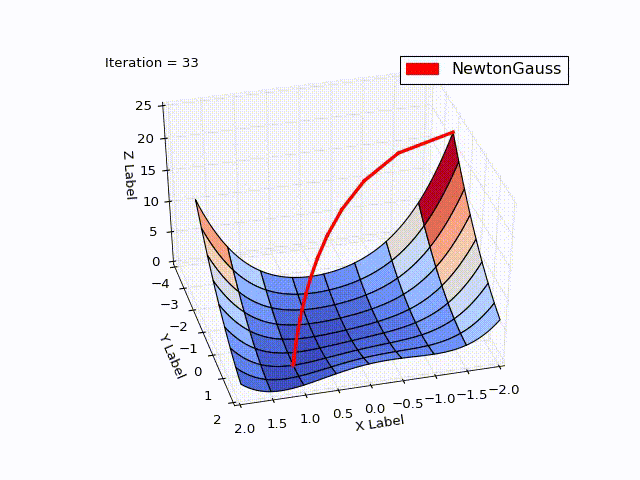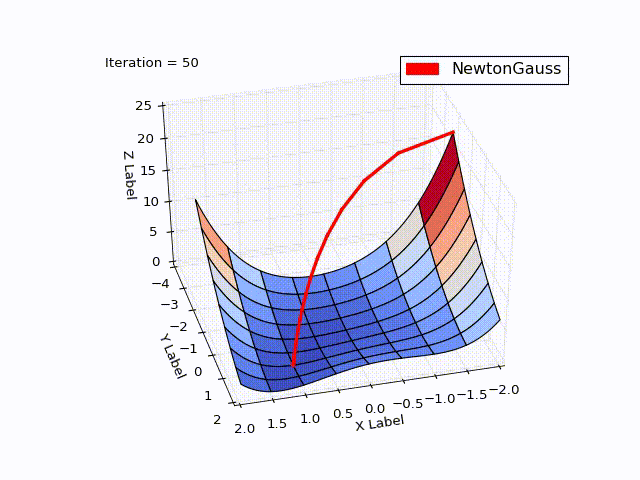
Алгоритм Левенберга — Марквардта
Он основан на одной из версий Методе Гаусса-Ньютона ("damped version" ):

Для больших 
Сам алгоритм в процессе оптимизации подбирает нужный 

Если 



Начальное значение 






В оптимизаторах я не реализовывал критерий остановки — за это отвечает пользователь. Мне нужно было только движение к следующей точке.
class LevenbergMarquardtOptimizer(Optimizer):
def __init__(self, function, initialPoint, gradient=None, jacobi=None, hesse=None,
interval=None, function_array=None, learningRate=1):
self.learningRate = learningRate
functionNew = lambda x: np.array([function(x)])
super().__init__(functionNew, initialPoint, gradient, jacobi, hesse, interval, function_array=function_array)
self.v = 2
self.alpha = 1e-3
self.m = self.alpha * np.max(self.getA(jacobi(initialPoint)))
def getA(self, jacobi):
return np.dot(jacobi.T, jacobi)
def getF(self, d):
function = self.function_array(d)
return 0.5 * np.dot(function.T, function)
def next_point(self):
if self.y==0: # Закончено. Y не может быть меньше нуля
return self.x, self.y
jacobi = self.jacobi(self.x)
A = self.getA(jacobi)
g = np.dot(jacobi.T, self.function_array(self.x)).reshape((-1, 1))
leftPartInverse = np.linalg.inv(A + self.m * np.eye(A.shape[0], A.shape[1]))
d_lm = - np.dot(leftPartInverse, g) # moving direction
x_new = self.x + self.learningRate * d_lm.reshape((-1)) # линейный поиск
grain_numerator = (self.getF(self.x) - self.getF(x_new))
gain_divisor = 0.5* np.dot(d_lm.T, self.m*d_lm-g) + 1e-10
gain = grain_numerator / gain_divisor
if gain > 0: # Ок, хорошая оптимизация
self.move_next(x_new) # ok, шаг принят
self.m = self.m * max(1 / 3, 1 - (2 * gain - 1) ** 3)
self.v = 2
else:
self.m *= self.v
self.v *= 2
return self.x, self.y
Результат получился тоже хороший:
| Итерация | X | Y | Z |
|---|---|---|---|
| 0 | -2 | -2 | 22.5 |
| 4 | 0.999 | 0.998 |  |
| 11 | 1 | 1 | 0 |
При learningrate =0.2:
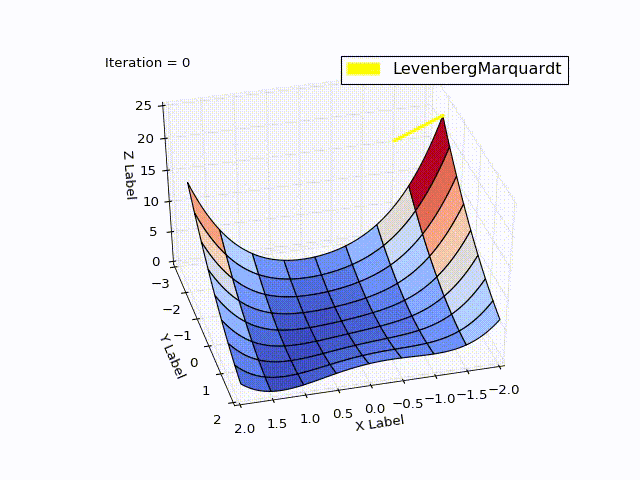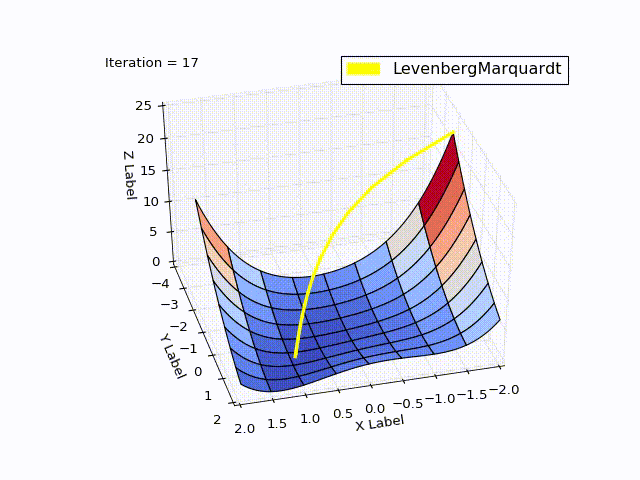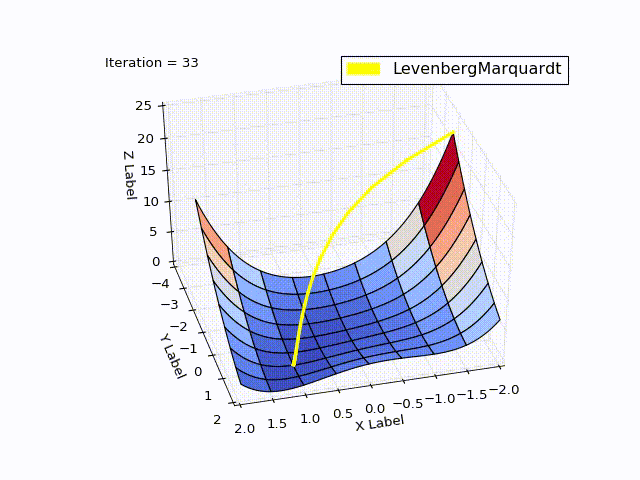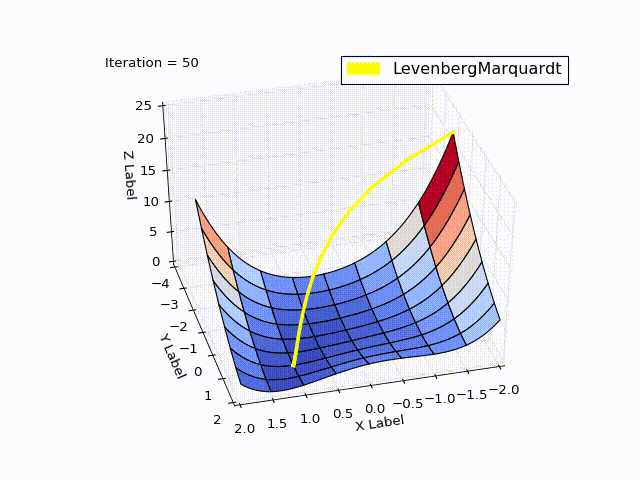
Сравнение методов
| Название метода | Целевая функция | Достоинства | Недостатки | Сходимость |
|---|---|---|---|---|
| Метод наискорейший спуск | дифференцируемая | -широкий круг применения -простая реализация -низкая цена одной итерации |
-глобальный минимум ищется хуже, чем в остальных методах
-низкая скорость сходимости вблизи экстремума |
локальная |
| Метод Нютона | дважды дифференцируемая | -высокая скорость сходимости вблизи экстремума
-использует информацию о кривизне |
-функция должны быть дважды дифференцируема
-вернёт ошибку, если матрица Гессе вырождена (не имеет обратной) -есть шанс уйти не туда, если находится далеко от экстремума |
локальная |
| Метод Гаусса-Нютона | нелинейный МНК | -очень высокая скорость сходимости
-хорошо работает с задачей curve-fitting |
-колонки матрицы J должны быть линейно-независимы
-налагает ограничения на вид целевой функции |
локальная |
| Алгоритм Левенберга — Марквардта | нелинейный МНК | -наибольная устойчивость среди рассмотренных методов
-наибольшие шансы найти глобальный экстремум -очень высокая скорость сходимости (адаптивная) -хорошо работает с задачей curve-fitting |
-колонки матрицы J должны быть линейно-независимы
-налагает ограничения на вид целевой функции -сложность в реализации |
локальная |
Несмотря на хорошие результаты в конкретном примере рассмотренные методы не гарантируют глобальную сходимость (найти которую — крайне трудная задача). Примером из немногих методов, позволяющих всё же достичь этого, является алгоритм basin-hopping
Совмещённый результат (специально понижена скорость последних двух методов):
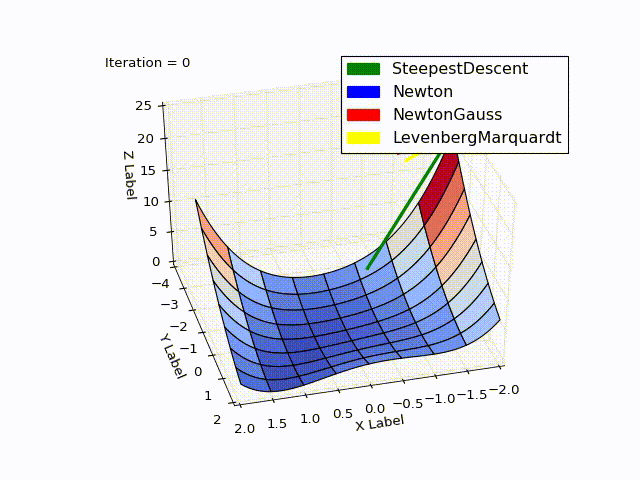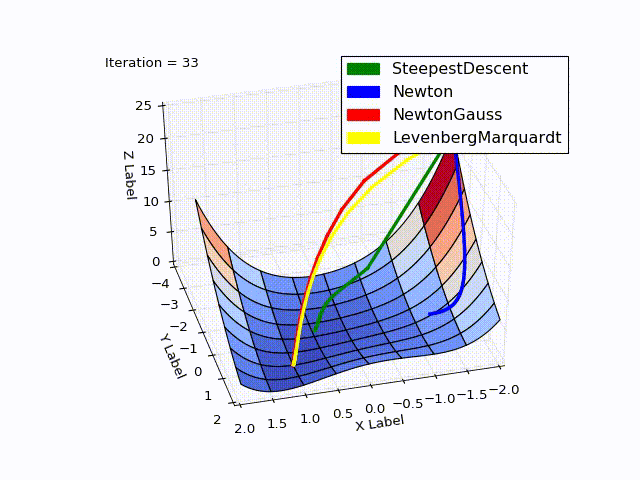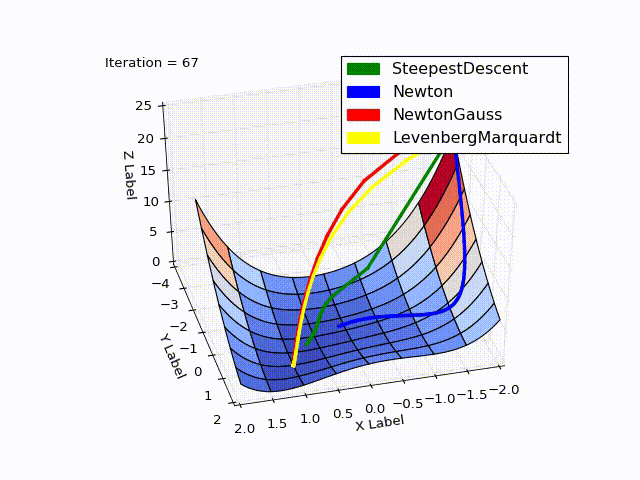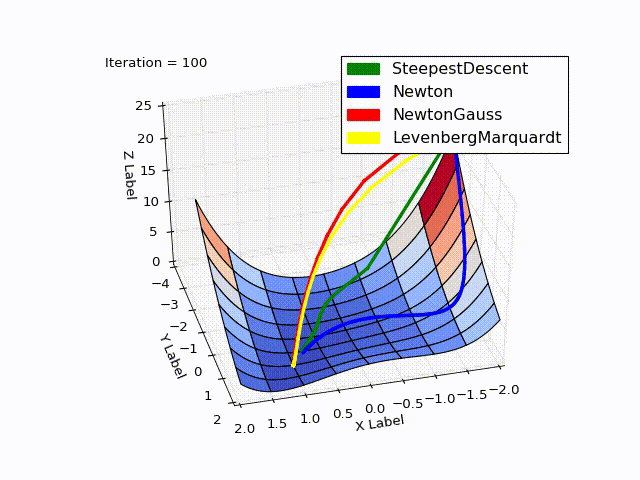
» Исходники можно скачать с github
» Источники
- K. Madsen, H.B. Nielsen, O. Tingleff (2004): Methods for non-linear least square
- Florent Brunet (2011): Basics on Continuous Optimization
- Least Squares Problems
Автор: lightforever2














