Нужно ли вам читать этот текст?
Давайте проверим. Прочтите следующее:
Тригонометрическим рядом Фурье функции
 называют функциональный ряд вида

где

Страшно, но всё же хочется понять, что это значит?
Значит, вам под кат. Постараюсь формул не использовать.
Мотивация
По моему глубокому убеждению, к математике можно подходить на двух уровнях: большинство людей её видит (им её именно так и преподают) как набор значков и правил операций над значками, что приводит к широким массам людей, математикой травмированных. А можно попытаться передать смысл и идеи, не особо заостряясь на значках. Лично я неспособен к синтаксическому подходу, я в цепи из двух формул обязательно потеряю какой-нибудь минус, что не мешает мне достаточно успешно считаться математиком. Просто у меня в голове графический ускоритель.
Я уже приводил цитату Фейнмана о том, как именно он читал все уравнения, что ему приходилось:
Actually, there was a certain amount of genuine quality to my guesses. I had a scheme, which I still use today when somebody is explaining
something that I'm trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they're all excited. As they're telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) — disjoint (two balls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn't true for my hairy green ball thing, so I say, «False!»
И при подготовке этого текста я наткнулся на замечательный доклад Анри Пуанкаре, который, пожалуй, был величайшим математиком конца девятнадцатого и начала двадцатого столетия. Он указывал, что даже в такой абстрактной науке, как математика, следует культивировать интуитивные понятия, например, понятие прямолинейности, хотя интуиция и должна проверяться формальными доказательствами.
Его доклад озаглавлен «Du rôle de l'intuition et de la logique en mathématiques», на французском можно прочитать тут, английский перевод доступен здесь. Крайне рекомендую интересующимся математикой, читается на одном дыхании.
К сожалению, передавать интуицию очень сложно, но я попытаюсь, так как выгода от переданной интуиции несравнимо выше от выгоды передачи просто значков.
На что я опираюсь в этом тексте
Перво-наперво нужно знать, что такое вектор, хотя бы на уровне «стрелочка». Ну и представлять, что стрелочки можно рисовать в существенно большем количестве размерностей, нежели 2 или 3. Ну и что хранить вектор можно в std::vector.
Затем центральным понятием является скалярное произведение.
На пальцах скалярное произведение можно представлять как меру того, насколько один вектор похож на другой. То есть, это операция, которая на вход берёт два вектора, на выход даёт число. Нормирование данных это уже детали, пока не очень нужные. Поэтому если у меня есть две стрелочки единичной длины, то скалярное произведение равно единице, если стрелочки совпадают, нулю, если они ортогональны и минус единице, если они противонаправлены.
Лирическое отступление
Это не просто лирика, это пример, который на первый взгляд не связан с темой разговора, но на самом деле является его сутью. Хотите понимать дальше — понимайте пример. Что неясно, задавайте вопросы.
Давайте на минуту рассмотрим крайне практическую задачу: у меня есть неспешный робот, и он должен знать, где он находится. Система навигации должна быть пассивной. Я люблю крайне дубовые решения, поэтому я ставлю на моего робота два микрофона (как уши у человека). Затем у меня есть маяк (на самом деле несколько, но давайте про один), который проигрывает в цикле некоторый (моно) звук. Например, вот такой:

Это просто сухие щелчки, положим для простоты один щелчок в секунду.
«Уши» робота находятся на разном расстоянии от маяка, а звук распространяется неспешно, поэтому каждый из двух микрофонов запишет плюс-минус один и тот же сигнал, но с небольшой задержкой один относительно другого. Я не ищу легких путей, поэтому у меня не лабораторные условия. Вот, например, как выглядит запись в течение нескольких секунд:
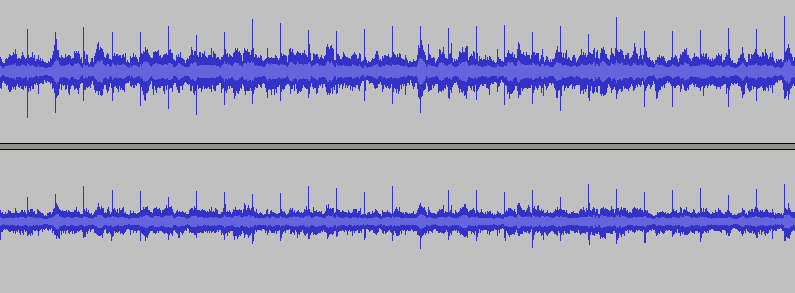
Два канала по количеству ушей, высокий уровень шума (играет музыка). На записи видно регулярные всплески сухих щелчков, но напрямую искать их в сигнале крайне непросто, иногда музыка бывает даже громче щелчков.
Как мне убрать фоновый шум? Напоминаю, робот у меня совсем неспешный. Самый дубовый способ — это записать час звука, затем порезать его на 3600 кусков в одну секунду длиной (у меня один щелчок в секунду), и взять среднее между всеми этими кусочками записи.
Получится нечто вот такое:
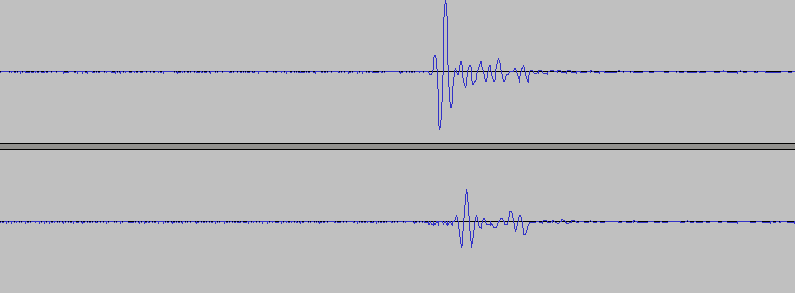
Пики щелчков приходятся в каждом из 3600 кусков на одно и то же место, а остальной шум размазан более-менее равномерно по всей длине, в итоге шум уходит. К слову сказать, маяков у меня несколько, никакой синхронизации между ними нет, а ушей только два. И именно так я и разделяю сигналы с маяков: один маяк щёлкает раз три раза в секунду, другой пять, третий семь. (Очень важно) Порезав один и тот же сигнал на кусочки в 1/3, в 1/5 или в 1/7 секунды, я получу сигнал именно с нужного маяка!
Итак, теперь мне нужно понять, как один сигнал сдвинут относительно другого. Мне абсолютно всё равно, в каком именно месте записи у меня пик, мне нужен сдвиг одного канала относительно другого.
Для начала давайте поймём, как я вообще представляю этот сигнал в памяти машины. Я пишу обычный wav с частотой дискретизации 44100Гц. Длина записи одна секунда, таким образом, у меня есть просто два массива (вектора!) вещественных чисел со 44100 элементами.
Фиксируем один вектор, а второй 44100 раз циклически сдвинем вправо. (Очень важно) Посчитаем 44100 скалярных произведения и возьмём тот сдвиг, при котором это скалярное произвдение максимально. То есть, именно этот сдвиг максимизирует похожесть двух сигналов. Поздравляю вас, вы только что посчитали взаимнокорреляционную функцию!
А теперь давайте считать ряд Фурье в уме
Предыдущая секция очень важна, но пока давайте её отложим и попробуем посчитать на пальцах простой ряд Фурье.
В качестве примера давайте возьмём простой квадратный сигнал, так любимый в электронике. Графики я рисую в sage.
def square_wave(t): return (sgn(sin(t))+1)/2
t = var('t')
plot(square_wave(t), (t, -10*pi, 10*pi),figsize=(10,2))

Это простой периодический сигнал с периодом в 2 pi. Половину времени он равен нулю, половину времени равен единице. Давайте считать коэффициенты ряда Фурье (см. начало статьи).
Нулевая частота
Коэффициент a0 — это просто среднее сигнала, очевидно, что он равен половине. Как считать a1 и b1?
Первая частота
А вот тут я предлагаю нарисовать один период нашего сигнала, но на сей раз не в обычной декартовой системе координат, но в полярной. Итого у нас угол идёт от нуля до двух пи, и мы получим следующую картинку:
parametric_plot((cos(t)*square_wave(t), sin(t)*square_wave(t)), (t, 0, 2*pi))
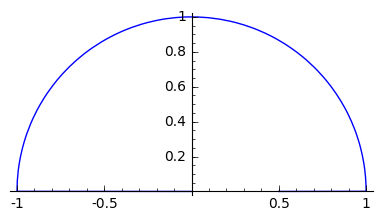
Почему в полярной системе? Очень просто. Как преобразуются полярные координаты точки (r,alpha) в декартовы?
x = r cos(alpha),
y = r sin(alpha).
А что у нас стоит под знаком интеграла в формуле для a1 и b1? Правильно, f sin(t) и f cos(t). Осталось проинтегрировать. Как это сделать в уме? Представьте, что у вас это не математический график, а отрезок проволоки. Давайте найдём его центр тяжести. Очевидно, что он будет лежать на оси ординат примерно в центре нашей дуги (на самом деле, на расстоянии 2/pi от центра, ну да это не суть, давайте назовём это расстояние A):
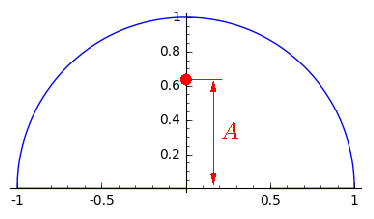
Координаты красной точки (центра тяжести графика) и есть нужные нам интегралы (с точностью до умножения на константу, ну да это не суть). Кстати, а можете сказать, почему именно так?
Итого a1 = 0, b1 = A.
Вторая частота
Что до a2 и b2? Давайте снова делать полярный график, «наматывая» наш обычный график вокруг нуля. Единственное, что теперь мы будем наматывать, делая два оборота.
Первый оборот:
parametric_plot((cos(2*t)*square_wave(t), sin(2*t)*square_wave(t)), (t, 0, pi))
parametric_plot((cos(2*t)*square_wave(t), sin(2*t)*square_wave(t)), (t, pi, 2*pi))
Второй оборот очевидно будет пустым, наш квадратный сигнал в этот момент равен нулю:

Центр масс первого + второго графиков лежит, очевидно, в нуле. Таким образом, a2=0, b2=0.
Третья частота
Теперь намотаем вокруг нуля один период нашей функции три раза, для наглядности я показываю три витка на раздельных графиках:

Первый виток заполняет полностью нашу окружность, второй наполовину, а третий пуст. Если один полный виток весит один килограмм, то мы имеем один килограмм в нуле и полкило на расстоянии A от нуля. Итого, центр тяжести будет на расстоянии A/3 от нуля.
a3 = 0
b3 = A/3
Более высокие частоты
Что будет с четвёртой частотой? Два заполненных витка и два пустых, центр в нуле. И так для всех чётных.
Что будет с пятой частотой? Два заполненных, два пустых и один полувиток. Итого центр тяжести на оси ординат на расстоянии A/5 от нуля.
Подводим итог
Если посмотреть ещё раз, как мы считаем интегралы, то станет понятно, что между нашим сигналом (квадратной волной) и функциями cos(nx), sin(nx) мы ищем скалярные произведения. То есть, мы смотрим, насколько наш сигнал похож на cos(nx) и насколько он похож на sin(nx). Наматывая определённое количество раз график (периодической!) функции вокруг нуля, мы гасим все частоты, кроме текущей.
Полярный угол нашего центра тяжести говорит, насколько сигнал похож на соответствующий синус или насколько он похож на соответствующий косинус. А расстояние, на котором находится центр тяжести, говорит о силе их вклада в формирование нашего сигнала.
Итого наш ряд равен f(x) = 1/2 + 2/pi sin(x) + 2/(3 pi) sin(3x) + 2/(5 pi) sin(5x) +…
Домашнее задание
1) Вы поняли связь между примером с роботом и квадратной волной?
2) А как связан ряд Фурье с преобразованием Фурье?
Автор: haqreu








