Добрый вечер, дорогиее, добрый вечер, славный город Белгород.
Расскажу я вам сегодня сказку об одном дураке. А дурак он (я, то беж) потому, что не следовал одной простой истине:
Знаменитая программистская лень заключается в том, что вместо лишних телодвижений (своих ли, машинных ли) лучше подумать и найти решение поизящнее и попроще.
А речь в ней пойдет о том, как дурак пытался научить находить положение камеры в пространстве.
Присказка
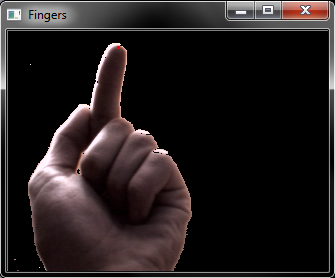
Надо было мне написать в конце второго курса проект по программированию. Решил я, как обычно, поохотиться за халяваой и примкнуть в конце года к какой-нибудь группе. Не получилось. Договорился с деканатом и препом о сдаче проекта в конце августа и спокойно уехал учить детей искусству. Вернувшись в Неризиновую, понял, что осталось у меня по сути две недели. С тех пор почти всё время я сидел в кофейне и занимался довольно приятным кодингом. Суть проекта заключалась в том, чтобы с помощью двух веб-камер в реальном времени определять пространственное положение концов пальцев.
Понятное дело, что каждому пикселю на изображении с камеры в пространстве соответствует какой-то луч в пространстве. Две камеры — внезапно два луча, пересекающиеся в интересующей нас точке. В теории всё просто. На практике я ночь прикручивал к MSVS библиотеку OpenCV, а потом полторы недели создавал различные алгоритмы обработки изображений, быстренько написал простейший 3D просмотрщик, скомпилировал две камеры вместе и отлаживал, отлаживал, отлаживал… В то время базис в пространстве я задавал легко — ставил камеры на одной линии, направлял их «примерно вверх» и считал расстояние между камерами за условные 1000 единиц.
В общем-то, всё было почти готово. Камеры по отдельности умели ловить единичный палец, причем с хорошей точностью, все мат.функции пересчета были вычислены, даже была написана фича, позволявшая иметь не черный, а почти любой неподвижный фон. Но что-то было не так — точка в пространстве выделывала причудливые кульбиты с амплитудой около сантиметра при движении рукой. Беда! И тут я понял, что официантка три часа назад просто чуть-чуть задела камеру.
Постановка
Я вздохнул и понял, что придется мне писать функцию, определяющую положение и ориентацию самой камеры. Область видимости камеры в идеале — бесконечная четырехугольная пирамида с прямоугольником в основании. Она полностью задается восемью величинами: 3 координаты вершины, 2 координаты вектора направления («биссектрисы» пирамиды, оси), 1 — поворот вокруг оси и еще 2 — угловая ширина обзора.
Последние две координаты изначально известны — гуглим угол обзора камеры по диагонали и решаем простейшую геометрическую задачку. Поворот вокруг оси — понятно что, но может меняться в зависимости от положения камеры. Координат вектора направления две, ибо его можно задавать как конец вектора определенной длины (3 координаты) и одна неизвестная уберется из уравнения x^2+y^2+z^2=l^2. Ну и три координаты вершины — понятно. Итого, нам надо вычислить 6 величин.
«О! Мне нужен треугольник!» — воскликнул я. 3 точки, и с каждой с изображения мы получаем по 2 числа. Итого план — мы ставим в пространстве какой-то равнобедренный прямоугольный треугольник и говорим, что его координаты (100, 0, 0), (0, 0, 0) и (0, 100, 0). Дальше отмечаем на изображении с камеры вершины этого треугольника и всё, что останется сделать — подставить значения в простенькую формулу. Ну, я так, во всяком случае думал.
Но не тут-то было. Я убил 4 часа на отыскание этой формулы обычными методами точной математики, подключил к поискам решения двоих лучших моих школьных друзей-математиков, стал набирать адрес Вольфрамальфы быстрее пароля, но всё, что я получил — что точное решение существует, единственно, но после его отыскания я познаю дзен.
И вот тут-то дурак и совершил ошибку. Там была система из 6 тригонометрических уравнений, тесно завязанных на уравнение окружности. А как раз в следующем семестре мы проходили ВычМаты, в которых, как известно, описан способ решения нелинейных систем. И правильно было бы почитать теорию и сделать всё как положено — несмотря на то, что времени займет больше, результат будет лучше и быстрее, да и полезно для саморазвития. Но нет, во мне проснулись замашки Петра I и я решил рубить топором.
Решение
Как известно из школьного курса планиметрии, ГМТ, из которых данный отрезок (AB) виден под данным углом (alpha) — дуга окружности. Рисунок всё проясняет.
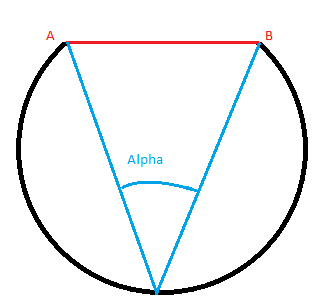
Плюс в пространстве эту картинку можно вращать вокруг отрезка. Получаем что-то вроде тора, только без дырки. Так как отрезка три, то мы получаем три тора, а, точнее, три торовых поверхности. Одна поверхность — плоская фигура, пересечение двух — уже линия (в общем случае — несколько замкнутых кривых), Три поверхности — уже точка. Торы на картинке чуть ниже.
Итак, топорный метод: мы должны пересечь эти три тора. А так как информатика дискретна, то придется нам поверхность тора представлять узлами натянутой на него сетки. Вот так:

Дальше в тупую сравниваются расстояния между точками и находится самые близкие друг к другу.
В итоге эта функция кушала памяти больше, чем вся остальная часть проекта со всеми отладочными изображениями и горами полунеобходимого мусора, работала по пять минут на одну камеру (да здравствует real-time!) и порой ошибалось.
А через пол-года я со скуки на паре таки написал функцию пересечения этих торов. Всё как положено, с вычматами, матрицами и прочим. Работала она мгновенно, считала точно и вообще была легкой и приятной. Но так как с тем проектом было кончено, написан он был на лету, с нулевым оформительством, а, значит, понять в тексте я ничего не смогу (тогда я еще боялся слова «class»), то исходник я оставил в кабинете. И вот пришло время наконец доделать этот проект, чем я, собственно, и занимаюсь. Но это уже совсем другая история.
До свидания, дорогиее, добрых снов, город Белгород.
P.S. В скором времени планирую описать алгоритмы обработки изображения — вот только сам вспомню их. Так что до скорых встреч!
Автор: gous32






