Гильоши — это характерные узоры на деньгах и ценных бумагах. Они красивы, и сочетают в себе одновременно заметную сложность с внутренней простотой — когда кажется, что ты вот-вот уловишь принцип, но он каждый раз от тебя ускользает. Возможно, именно это и есть определение красоты.
Поскольку гильоши использовались как средство защиты ценных бумаг от подделки, все, что связано с их использованием, было засекречено, и информацию приходится собирать по крупицам.
Само название происходит от фамилии французского инженера Гилльо (Guillot), о котором не осталось никаких сведений. Не исключено, что это вообще чисто мифическая фигура.
Первоначально гильоши использовались для гравировки волнистых линий на корпусах часов, яйцах Фаберже и тому подобных предметах, на которых требуются строгие геометрические украшения. Выполнялись они некоторой разновидностью токарного станка, в которой резец не был жестко закреплен, а описывал фигуры вокруг крутящейся заготовки.
Примерно в середине XIX века кому-то пришла в голову идея приспособить такой станок для генерации сложных узоров на типографской пластинке. Скорее всего, это были американцы, поскольку на их деньгах гильоши появились раньше всего — на выпуске 1862 года, и очень быстро стали одним из главных элементов дизайна.

Постепенно их заимствовали почти все развитые страны — кроме Франции, которая придерживалась исключительно живописной манеры рисования банкнот, не отвлекаясь на механические штучки.
На российских деньгах гильоши первый раз были напечатаны в выпуске 1892 года.

Если рассматривать сами узоры на деньгах разных стран, то можно заметить, что, несмотря на общий принцип, они довольно сильно различаются. Отсюда можно сделать вывод, что каждый разрабатывал соответствующие станки самостоятельно. Заметна и корреляция — чем развитее страна, тем ее гильоши сделаны лучше. Для примера достаточно посмотреть на румынские деньги времен Чаушеску, где для гильошировочной машины, похоже, использовались детали от трактора.

Создание гильошей было сложным делом — настолько сложным, что этим занимались отдельные люди, имевшие особую профессию гильошировщика. По некоторым сведениям можно понять, что гильошировщики рисовали гильош по эскизу художника — это видно из приводимого примера наброска и готовой банкноты в 1 червонец 1926 года. Не удивлюсь, если они это делали путем механической подгонки деталей, а то и вообще перебирали машину заново.


Сейчас гильоши из моды вышли, поскольку они могут противостоять только рисованию денег руками — попробуй чернилами вычертить все эти мелкие кривые. При использовании оптического копирования они бесполезны — сканеру все равно, что считывать: узоры или портреты. Так что на современных банкнотах гильошей обычно уже нет или они скромно торчат где-нибудь в углу как дань традиции.
Вычислить алгоритм для рисования гильошей крайне сложно — хотя на вид они кажутся достаточно простыми. Во многих источниках пишут, что это всего лишь усложненная версия спирографа с несколькими колесами, но я в этом сильно сомневаюсь. Многоколесный спирограф несложно повторить на компьютере, но получающиеся узоры во-первых, нисколько гильоши не напоминают, а во-вторых, их невозможно подогнать к заранее заданным контурам.
Ясно, что гильош — это семейство синусоид, сдвинутых по фазе относительно друг друга, и искажающихся в зависимости от внешних контуров так, чтобы не переходить их границы. Это очевидно — но совсем не очевидно, как именно математически контуры на синусоиды влияют.
На самом деле принцип построения узоров довольно прост, но несколько странноват. Они считаются по точкам, причем простых алгебраических операций над тремя кривыми (внутренним, внешним контуром и синусоидой, стелящейся между ними) недостаточно — нужно еще решать уравнения, чтобы определить пересечение линии и кривой.
Собственно, в каждой точке мы ставим точку синусоиды, но каждый раз разной — как бы модулированной текущим состоянием ограничивающих контуров.
Как именно необходимые вычисления выполнялись на механических станках, выше моего понимания.
Итак, принцип рисования. Мы начнем с горизонтального гильоша, потому что он проще. Внимание на экран.

Зеленым цветом выделены контуры, ограничивающие наш гильош. Будем считать их нижним и верхним и рассчитаем значение точки гильоша в абсциссе t.
Прежде всего найдем точки PB и PT — точки контуров при t. Заодно высчитаем в этом месте векторы направления кривых.
Теперь найдем некую среднюю точку Mid между нижним и верхним контуром. Именно от нее будет отсчитываться рисование нашей красивой кривой. Мы можем взять просто точку, среднюю между PB и PT, а можем еще умножить ее на некий коэффициент 0..1, показывающий, в какой пропорции следует учитывать нижний и верхний контур. Тогда мы сможем чуть смещать гильош вверх-вниз между контурами, чтобы добиться более красивых фигур.
Высчитаем в этой точке вектор направления как средний между векторами в точках PB и PT. Найдем для него перпендикуляр.
Посчитаем значение самой обыкновенной синусоиды в точке t (в предположении, что она начинается в точке 0,0 и движется вдоль оси ординат вправо).
Теперь исказим эту синусоиду следующим образом: перенесем текущее значение ее аргумента (t,0) в точку Mid, ее осью X сделаем «средний вектор», а осью Y, соответственно, перпендикуляр к нему. Тогда ее текущая точка окажется в точке RP.
Осталось только смодулировать амплитуду этой синусоиды. Посчитаем расстояние Mid--IP, то есть расстояние от средней точки до первой точки пересечения перпендикуляра с контуром. Какой контур брать, верхний или нижний, мы определим по значению исходной синусоиды — находится она выше оси ординат или ниже. На рисунке изображен случай, когда значение эталонной синусоиды больше нуля и мы используем верхний контур.
Теперь масштабируем Mid--RP, считая расстояние Mid--IP единицей, и отложим это значение вдоль новой оси ординат, т.е. по перпендикуляру. Мы получим точку GP — она и будет искомой точкой гильоша.
Перейдем к программированию. Вот программа рисования горизонтального гильоша на языке Asymptote:
import graph;
import wave;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(2);
var zero = (0,0);
typedef pair pairf(real x);
///////////////////////////////////////////
// Единичный вектор, перпендикулярный к вектору (0,0)--v
pair orthogonal(pair v)
{
return unit((-v.y,v.x));
}
// Точка и направление кривой в точке с координатами x,path(x)
pair[] pt_and_dir(path p, real x)
{
var t = times(p,x)[0];
return new pair[]{point(p,t), dir(p,t)};
}
// Функция, рассчитывающая точку гильоша в точке с абсциссой t
pairf between(path top, path bottom, real topk=0.5, real phase, real omega)
{
return new pair(real t)
{
// Точка и направление верхнего и нижнего контура
var pdt = pt_and_dir(top,t);
var pdb = pt_and_dir(bottom,t);
// "Средняя" точка как смесь из верхней и нижней
var mid = topk*pdt[0] + (1-topk)*pdb[0];
// Выведем для наглядности среднюю точку
draw(mid,gray);
// Вектор, перпендикулярный смеси направлений верхней и нижней точки
var ort = orthogonal(topk*pdt[1] + (1-topk)*pdb[1]);
// Точка на обычной синусоиде, которую мы сейчас будем модулировать
var f = sin(phase+omega*t);
// Вектор, в сторону которого модуляция отклонит точку
var rp = rotate(degrees(atan2(ort.y,ort.x)-pi/2),zero) * (0,f);
// Рассчитываем точку пересечения перпендикулярного вектора с одним из контуров
// Для этого узнаём все точки пересечения и берем из них ближайшую
var ipath = rp.y >= 0 ? top : bottom;
var inter = intersections(ipath,mid,mid+ort);
var interp = sequence(new pair(int i) {return point(ipath,inter[i]); }, inter.length);
interp = sort(interp, new bool(pair a, pair b) {return abs(mid.x-a.x) < abs(mid.x-b.x); });
var ip = interp[0];
// Узнаем расстояние от "средней точки" до точки пересечения перпендикулярного вектора с контуром
var r = sqrt((mid.x-ip.x)*(mid.x-ip.x)+(mid.y-ip.y)*(mid.y-ip.y));
// Модулируем синусоиду
return mid+r*rp;
};
}
// Рисуем гильош несколько раз со сдвигом
void repeat(int n, path top, path bottom, real topk, real freq)
{
var step = 2pi/n;
for (var i: sequence(0,n))
{
draw(graph(between(top,bottom, topk, i*step, freq), 0,8, 500));
}
}
// Верхний контур - просто что-то типа синусоиды
path top = shift(0,0.3)*(4*make_wave(1.4, (+1,+0.7),(+1,-0.7) ));
// Нижний - прямая
path bottom = (0,0)--(8,0);
draw(top, blue);
draw(bottom, blue);
// укладываем между ними 9 "синусоид" с частотой 11, проходящих точно посередине между верхним и нижним контуром
repeat(9, top, bottom, 0.5, 11);
А вот результат ее работы. Изящно.

С круговыми гильошами — как раз теми, что обычно фигурируют на деньгах — дело усложняется. Принцип остается тем же, но…
1. Вместо декартовых координат приходится работать в полярных
2. Кривые становятся капризными и начинают себя плохо вести. При более-менее сложных контурах в некоторых точках возникает ситуация, когда перпендикуляр вовсе не пересекается с нужным контуром. Очевидно, в таких случаях и требуется многолетний опыт гильошировщика.
Итак, программа. Обратите внимание, что в ней контуры по аналогии с предыдущей программой называются верхним и нижним, хотя реально они внешние и внутренние.
import graph;
import wave;
size(1000,1000);
xaxis(ticks=Ticks);
yaxis(ticks=Ticks);
defaultpen(5);
var zero = (0,0);
typedef pair pairf(real x);
typedef pair[] pairaf(real t);
///////////////////////////////////////////
// Определение перпендикулярного вектора
pair orthogonal(pair v)
{
return unit((-v.y,v.x));
}
// Пересчет полярных координат в декартовые
pair cart(real a, real r)
{
return (r*cos(a), r*sin(a));
}
// Нормализованный угол по вектору-направлению
real atan2p(pair v)
{
var a = atan2(v.y,v.x);
return a<0 ? a+2pi : a;
}
// Расстояние между двумя точками
real distance(pair a, pair b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
// Точка и вектор направления на пути p при полярном угле a
pair[] pt_and_dir(path p, real a)
{
var ii = intersections(p,zero--cart(a,100));
if (ii.length==0)
{
write(p);
write(a);
}
var t = ii[0];
return new pair[]{point(p,t[0]), dir(p,t[0])};
}
// Вычисление точек гильоша, если имеется функция midpoint, рассчитывающая координаты и направление в средней точке
pairf between(path top, path bottom, pairaf midpoint, real phase, real omega)
{
return new pair(real t)
{
var b = midpoint(t);
var mid = b[0];
draw(mid,green);
var mid_dir = b[1];
var f = sin(phase+omega*t);
var angle = (degrees(atan2p(mid_dir))+180) % 360;
var rp = rotate(angle,zero) * (0,f);
//На какой контур смотрит вектор нашей точки синусоиды - на верхний или нижний?
var ipath = distance(mid+rp,zero) > distance(mid,zero) ? top : bottom;
// Найдем точки пересечения перпендикуляра с контуром
var inter = intersections(ipath,mid,mid+rp);
// Вот тут-то и засада. Пересечений с контуром может вообще не быть. Выводим тогда линию противного цвета,
// чтобы это было сразу заметно
if (inter.length==0)
{
draw(mid--mid+rp,magenta,Arrow);
return mid;
}
// Отсортируем точки пересечения и найдем самую ближнюю
var interp = sequence(new pair(int i) {return point(ipath,inter[i]); }, inter.length);
interp = sort(interp, new bool(pair a, pair b) {return distance(mid,a) < distance(mid,b); });
var ip = interp[0];
var r = distance(mid,ip);
return mid + r*rp;
};
}
// Вычисление точек гильоша, если задан средний путь
pairf between(path top, path bottom, path base, real phase, real omega)
{
pairaf mf = new pair[](real t) { return pt_and_dir(base, t); };
return between(top, bottom, mf, phase, omega);
}
// Вычисление точек гильоша, если дан коэффициент смешивания верхнего и нижнего контуров
pairf between(path top, path bottom, real topk=0.5, real phase, real omega)
{
pairaf midpoint = new pair[](real t)
{
var pdt = pt_and_dir(top,t);
var pdb = pt_and_dir(bottom,t);
var mid = topk*pdt[0] + (1-topk)*pdb[0];
var mid_dir = topk*pdt[1] + (1-topk)*pdb[1];
return new pair[]{mid, mid_dir};
};
return between(top, bottom, midpoint, phase, omega);
}
// Рисование гильоша с вычислением средней линии (как в программе с горизонтальным гильошем)
void repeat(int n, path top, path bottom, real topk, real freq)
{
var step = 2pi/n;
for (var i: sequence(0,n-1))
{
draw(graph(between(top,bottom, topk, i*step, freq), 0, 2pi, 500));
}
}
// Вариант - средняя линия не вычисляется, а задается отдельным путем
void repeat(int n, path top, path bottom, path base, real freq)
{
var step = 2pi/n;
for (var i: sequence(0,n-1))
{
draw(graph(between(top,bottom,base, i*step, freq), 0, 2pi, 500));
}
}
// Контуры - внешний и внутренний. Чтобы не возиться с вычислением их координат, я просто обвел их в векторном редакторе,
// сохранил как SVG и извлек из текста описание пути
path top = (458.43,237.715)..controls (468.922,264.461) and (481.563,290.133)..(466.797,322.145)
..controls (438.688,358.184) and (392.762,345.094)..(362.438,351.945)
..controls (354.488,353.742) and (350.508,354.398)..(342.07,358.234)
..controls (338.023,360.074) and (333.797,358.609)..(329.125,358.598)
..controls (324.457,358.582) and (319.348,360.02)..(315.824,363.094)
..controls (306.16,371.52) and (294.707,387.746)..(278.176,400.949)
..controls (261.645,414.152) and (250.875,417.965)..(236.914,417.996)
..controls (222.957,418.023) and (213.074,414.152)..(196.543,400.949)
..controls (180.012,387.746) and (168.559,371.52)..(158.895,363.094)
..controls (155.371,360.02) and (150.262,358.582)..(145.594,358.598)
..controls (140.922,358.609) and (136.695,360.074)..(132.648,358.234)
..controls (124.211,354.398) and (120.23,353.742)..(112.281,351.945)
..controls (81.957,345.094) and (36.0313,358.184)..(7.92188,322.145)
..controls (-6.84375,290.133) and (5.79688,264.461)..(16.2891,237.715)
..controls (19.1992,230.289) and (11.7227,218.836)..(11.7227,209.773)
..controls (11.7227,200.711) and (19.1992,188.906)..(16.2891,181.48)
..controls (5.79688,154.734) and (-6.84375,129.063)..(7.92188,97.0508)
..controls (36.0313,61.0078) and (81.957,74.0977)..(112.281,67.2461)
..controls (120.23,65.4531) and (124.211,64.7969)..(132.648,60.9609)
..controls (136.695,59.1211) and (140.922,60.582)..(145.594,60.5977)
..controls (150.262,60.6094) and (155.371,59.1719)..(158.895,56.1016)
..controls (168.559,47.6719) and (180.012,31.4492)..(196.543,18.2461)
..controls (213.074,5.03906) and (222.957,1.16797)..(236.914,1.19922)
..controls (250.875,1.22656) and (261.645,5.03906)..(278.176,18.2461)
..controls (294.707,31.4492) and (306.16,47.6719)..(315.824,56.1016)
..controls (319.348,59.1719) and (324.457,60.6094)..(329.125,60.5977)
..controls (333.797,60.582) and (338.023,59.1211)..(342.07,60.9609)
..controls (350.508,64.7969) and (354.488,65.4531)..(362.438,67.2461)
..controls (392.762,74.0977) and (438.688,61.0078)..(466.797,97.0508)
..controls (481.563,129.063) and (468.922,154.734)..(458.43,181.48)
..controls (455.52,188.906) and (462.996,200.238)..(463.055,209.359)
..controls (463.113,218.48) and (455.52,230.289)..(458.43,237.715)
--cycle;
path bottom = (435.121,232.246)..controls (424.465,250.848) and (436.73,269.879)..(418,294.242)
..controls (399.266,318.602) and (368.48,321.363)..(355.004,331.102)
..controls (341.531,340.84) and (349.316,349.461)..(338.301,353.699)
..controls (327.289,357.934) and (311.055,338.211)..(297.848,342.762)
..controls (277.797,349.668) and (257.313,362.477)..(235.926,362.551)
..controls (214.543,362.629) and (196.012,350.156)..(175.961,343.25)
..controls (162.75,338.699) and (146.52,358.422)..(135.504,354.188)
..controls (124.492,349.949) and (132.277,341.328)..(118.805,331.59)
..controls (105.328,321.852) and (74.5391,319.09)..(55.8086,294.73)
..controls (37.0742,270.367) and (49.3438,251.336)..(38.6875,232.734)
..controls (33.918,224.414) and (17.0078,213.824)..(17.0078,209.363)
..controls (17.0078,204.902) and (33.9258,194.051)..(38.6953,185.727)
..controls (49.3555,167.129) and (37.082,148.094)..(55.8242,123.734)
..controls (74.5625,99.375) and (105.359,96.6094)..(118.84,86.875)
..controls (132.32,77.1367) and (124.531,68.5117)..(135.547,64.2773)
..controls (146.566,60.043) and (162.805,79.7617)..(176.016,75.2148)
..controls (196.078,68.3086) and (214.613,55.832)..(236.008,55.9102)
..controls (257.398,55.9883) and (277.891,68.7969)..(297.953,75.7031)
..controls (311.164,80.2539) and (327.402,60.5313)..(338.418,64.7656)
..controls (349.438,69.0039) and (341.648,77.625)..(355.129,87.3633)
..controls (368.609,97.0977) and (399.406,99.8633)..(418.145,124.223)
..controls (436.887,148.586) and (424.613,167.617)..(435.273,186.219)
..controls (440.043,194.539) and (456.961,205.215)..(456.926,209.535)
..controls (456.887,213.859) and (439.891,223.926)..(435.121,232.246)
--cycle;
// Подгоняем под масштаб нашего рисунка
top = scale(1/10)*top;
bottom = scale(1/10)*bottom;
// И смещаем контуры из центра координат в левый верхний квадрант
var min = min(top);
var max = max(top);
top=shift(-(max.x-min.x)/2, -(max.y-min.y)/2)*top;
min = min(bottom);
max = max(bottom);
bottom=shift(-(max.x-min.x)/2-min.x, -(max.y-min.y)/2-min.y)*bottom;
draw(top, blue);
draw(bottom, blue);
// Пускаем 4 синусоиды
repeat(4, top, bottom, 0.5, 18);
Результат — нечто похожее на розетку с купона в 25 белорусских рублей 1992 года. Можно сделать еще похожей, если самому аккуратно нарисовать среднюю линию (см. второй рисунок).
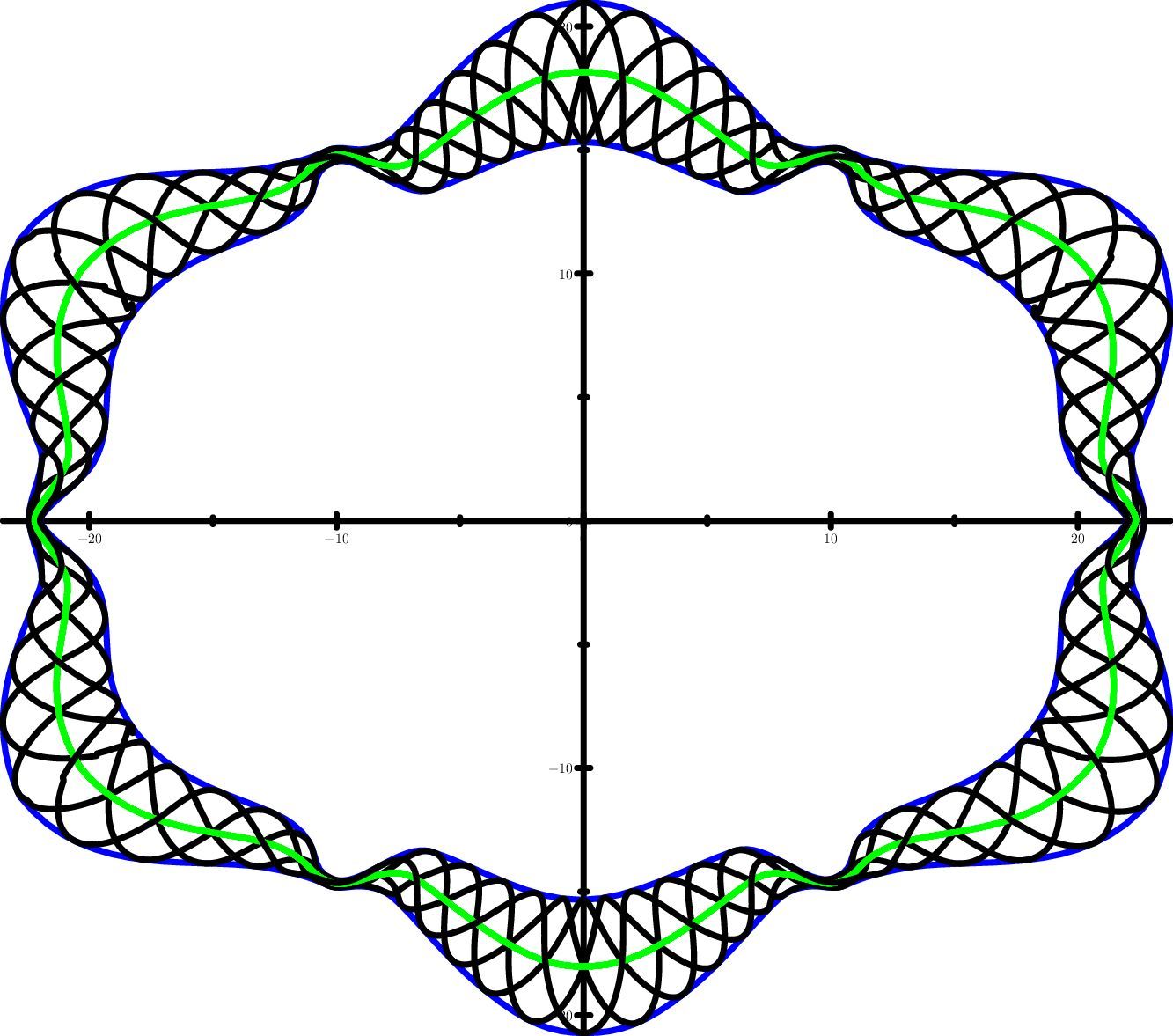

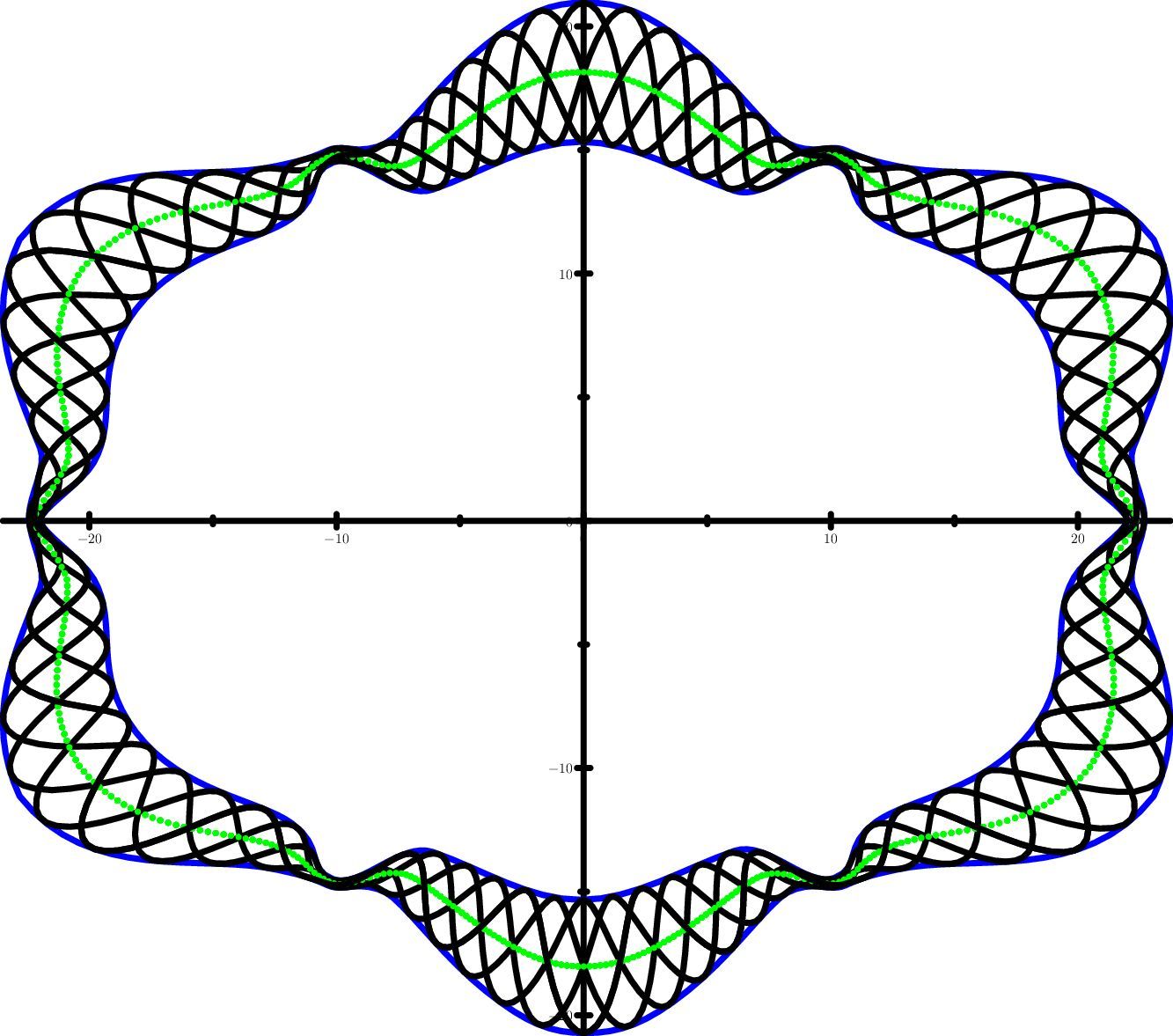
Некоторые линии на нашем рисунке получились с зазубринами — это из-за недостатка точности вычислений. В какой-то степени их можно исправить, поставив в операторе draw расчет не 500, а 10000 точек.
Что можно еще придумать с гильошами?
Во-первых, если внимательно посмотреть на белорусскую версию, то заметно, что тамошние узоры еще меняют свою частоту — они становятся то гуще, то реже. Как учитывать частоту в моей программе — я так и не придумал.
Во-вторых, гильоши прямо-таки напрашиваются быть сохраненными в виде кривых Безье — они очень хорошо ими аппроксимируются. Но для этого надо понимать, как они себя ведут — где у них вершины, где точки перегиба. Вычислять это из набора точек как-то глупо, а как подойти к вопросу математически, например, посчитав производную, — непонятно.
Если у многоуважаемой публики есть на этот счет какие-то соображения, прошу делиться.
P.S. Рисунки в статье отмасштабированы, чтобы не портить общий вид страницы. Вы можете открыть их отдельно и рассмотреть с лучшим разрешением.
Автор: gatoazul
