Это седьмая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре:
- Теория категорий для программистов: предисловие
- Категория: суть композиции
- Типы и функции
- Категории, большие и малые
- Категории Клейсли
- Произведения и копроизведения
- Простые алгебраические типы данных
Функторы
За понятием функтора стоит очень простая, но мощная идея (как бы заезжено это ни прозвучало). Просто теория категорий полна простых и мощных идей. Функтор есть отображение между категориями. Пусть даны две категории C и D, а функтор F отображает объекты из C в объекты из D — это функция над объектами. Если a — это объект из C, то будем обозначать его образ из D как F a (без скобок). Но ведь категория — это не только объекты, но еще и соединяющие их морфизмы. Функтор также отображает и морфизмы — это функция над морфизмами. Но морфизмы отображаются не как попало, а так, чтобы сохранять связи. А именно, если морфизм f из C связывает объект a с объектом b,
f :: a -> bто образ f в D, F f, связывает образ a с образом b:
F f :: F a -> F b(Надеемся, что такая смесь математических обозначений и синтаксиса Haskell понятна читателю. Мы не будем писать скобки, применяя функторы к объектам или морфизмам.)
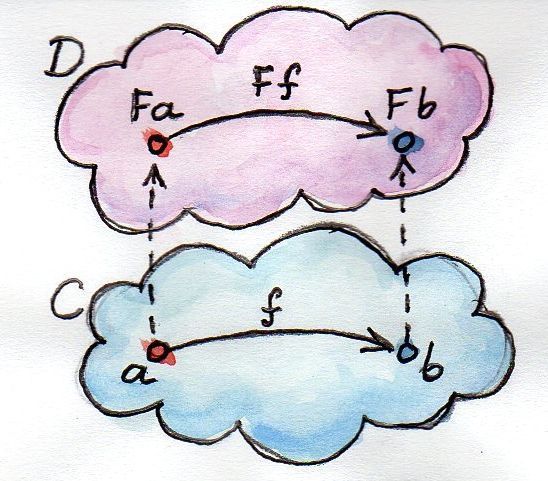
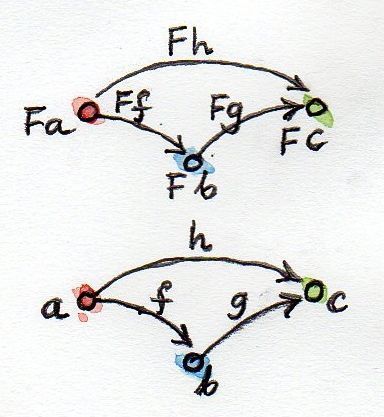
Как видите, функтор сохраняет структуру: что было связано во входной категории, будет связано и в выходной. Но этим структура не исчерпывается: необходимо также поддержать композицию морфизмов. Если h — композиция f и g:
то потребуем, чтобы его образ под действием F был композицией образов f и g:
F h = F g . F f
Наконец, потребуем, чтобы все единичные(тождественные) морфизмы из C отображались в единичные морфизмы из D:
F id(a) = id(F a)Здесь ida — это единичный морфизм объекта a, а idF a — единичный морфизм объекта F a.
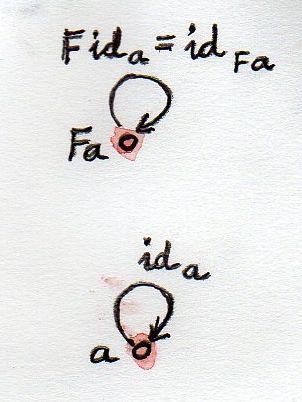
Заметим, что все эти условия существенно ограничивают круг функций, подходящих в качестве морфизмов. Функторы должны сохранять структуру категории. Если представить себе категорию как набор объектов, переплетенных морфизмами, то функтор не имеет права оборвать ни одной нити этого кружева. Он может объединить несколько объектов, он может склеить морфизмы в один, но никогда не разрывает связей. Это ограничение аналогично понятию непрерывности из математического анализа. В этом смысле функторы "непрерывны" (хотя существует еще более ограничивающее определение непрерывности функторов). Как и любая функция, функтор может быть и склеивающими, и вкладывающими. Аспект вложения наиболее ярко проявляется, когда исходная категория намного меньше целевой. В предельном случае исходная категория представляет собой категорию 1, состоящую из одного объекта и одного (единичного) морфизма. Функтор из категории 1 в любую другую категорию просто выбирает определенный объект из этой категории. Имеет место полная аналогия с морфизмами из синглтона, выбирающими элементы из целевых множеств. Аспект склеивания, доведенный до абсурда, наблюдается в константном функторе Δc. Он отображает каждый объект исходной категории в определенный объект c целевой категории, а всякий морфизм — в единичный морфизм idc. Это как черная дыра, засасывающая все в точку сингулярности. Мы вернемся к рассмотрению этого функтора при обсуждении пределов и копределов.
Функторы в программировании
Вернёмся на землю, в мир программирования. Итак, у нас есть категория типов и функций. Рассмотрим функторы, отображающие эту категорию в себя — так называемые эндофункторы. Что представляет собой эндофунктор в категории типов? В первую очередь, он сопоставляет одним типам другие. Подобные отображения на самом деле нам знакомы, это типы, параметризованные другими типами. Рассмотрим несколько примеров.
Функтор Maybe
Определение Maybe есть отображение типа a в тип Maybe a:
data Maybe a = Nothing | Just aВажная деталь: Maybe сам по себе — это не тип, а конструктор типа. Он принимает в качестве аргумента тип, такой как Int или Bool, и возвращает другой тип. Maybe без аргументов представляет собой функцию на типах. Но является ли Maybe функтором? (Здесь и далее, говоря о функторах в контексте программирования, почти всегда подразумеваются эндофункторы.) Ведь функтор — это не только отображение объектов (здесь — типов), но и отображение морфизмов (здесь — функций). Для любой функции из a в b
f :: a -> bхотелось бы получить функцию из Maybe a в Maybe b. Чтобы определить такую функцию, нужно рассмотреть два случая, соответствующие двум конструкторам Maybe. В случае Nothing мы просто возвращаем Nothing обратно. Если же аргумент является Just, то применим функцию f к его содержимому. Итак, образ f под действием Maybe — это функция
f’ :: Maybe a -> Maybe b
f’ Nothing = Nothing
f’ (Just x) = Just (f x)(Кстати, в Haskell разрешено использовать апострофы в именах переменных, что очень удобно в подобных случаях.) В Haskell обличье функтора, отвечающее за отображение морфизмов, реализуется функцией высшего порядка fmap. Для Maybe она имеет следующую сигнатуру:
fmap :: (a -> b) -> (Maybe a -> Maybe b)
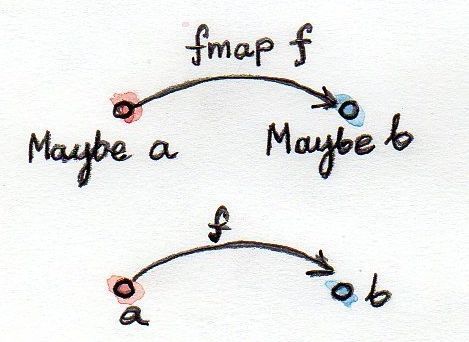
Часто говорят, что fmap возвышает (поднимает, lifts) функцию. Возвышенная функция работает на Maybe-значениях. Как обычно, из-за каррирования эта сигнатура может трактоваться двояко: либо как функция одной переменной, которая сама является функцией (a->b), возвращающая функцию (Maybe a -> Maybe b), либо как функция двух переменных, возвращающая Maybe b:
fmap :: (a -> b) -> Maybe a -> Maybe b Следуя сказанному выше, дадим определение fmap для Maybe:
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)Чтобы показать, что конструктор типов Maybe вместе с функцией fmap составляют функтор, осталось доказать, что fmap сохраняет единичные морфизмы и композицию. Эти утверждения называются "функториальными законами", но они просто удостоверяют сохранение структуры категории.
Метод эквивалентных преобразований
Докажем функториальные законы методом эквивалентных преобразований, который является типичной техникой доказательств в Haskell. Метод опирается на то, что функции в Haskell определены набором равенств: левая часть равна правой, обе они могут быть подставлены друг вместо друга (возможно, при подстановке потребуется переименовать переменные во избежание конфликтов). Можно как подставить тело функции вместо ее вызова (инлайнинг), так и вызов функции вместо ее тела (рефакторинг). Рассмотрим в качестве примера тождественную функцию:
id x = xЕсли мы встретим где-либо, скажем, id y, то его всегда можно заменить на y (инлайнинг). И вообще любое вхождение id, примененного к выражению, например, id (y + 2), можно заменить на само это выражение (y + 2). В обратную сторону: любое выражение e можно заменить на id e (рефакторинг). В случае функций, определенных при помощи сопоставления с образцом, можно использовать каждое определение независимо. Например, согласно данному выше определению fmap можно заменить fmap f Nothing на Nothing или наоборот. Рассмотрим этот подход на практике. Начнём с сохранения тождественности:
fmap id = idСледует рассмотреть два случая: Nothing и Just. Начнём с Nothing (Я описываю трансформацию левой части равенства в правую используя псевдо-Haskell):
fmap id Nothing
= { по определению fmap }
Nothing
= { по определению id }
id NothingЗаметьте, что на втором шаге мы подставили id Nothing вместо Nothing, используя определение id в обратную сторону. На практике подобные доказательства делаются методом "поджигания фитиля с двух концов", вплоть до встречи в середине на одном и том же выражении, Nothing в данном случае. Второй случай также несложен:
fmap id (Just x)
= { по определению fmap }
Just (id x)
= { по определению id }
Just x
= { по определению id }
id (Just x)Теперь покажем, что fmap сохраняет композицию:
fmap (g . f) = fmap g . fmap fНачнём со случая Nothing:
fmap (g . f) Nothing
= { по определению fmap }
Nothing
= { по определению fmap }
fmap g Nothing
= { по определению fmap }
fmap g (fmap f Nothing)Теперь пришло время Just:
fmap (g . f) (Just x)
= { по определению fmap }
Just ((g . f) x)
= { по определению композиции }
Just (g (f x))
= { по определению fmap }
fmap g (Just (f x))
= { по определению fmap }
fmap g (fmap f (Just x))
= { по определению композиции }
(fmap g . fmap f) (Just x)Стоит подчеркнуть, что для функций с побочными эффектами в стиле С++, метод эквивалентных преобразований не работает. Рассмотрим пример:
int square(int x) {
return x * x;
}
int counter() {
static int c = 0;
return c++;
}
double y = square(counter());Метод эквивалентных преобразований позволил бы развернуть square и получить
double y = counter() * counter();Определенно, такая трансформация некорректна и меняет результат выражения. Несмотря на это, если определить square как макрос, препроцессор C++ воспользуется методом эквивалентных преобразований с катастрофическим результатом.
Снова Maybe
Функторы легко выражаются в Haskell, но описывать их можно на любом языке, поддерживающем обобщённое программирование и функции высшего порядка. Рассмотрим С++ -ный аналог Maybe, шаблонный тип optional. Вот набросок реализации (полная реализация много сложнее, поскольку явно описывает разные способы передачи аргументов, семантику копирования и прочие вопросы характерного для С++ управления ресурсами):
template<class T>
class optional {
bool _isValid; // the tag
T _v;
public:
optional() : _isValid(false) {} // Nothing
optional(T x) : _isValid(true) , _v(x) {} // Just
bool isValid() const { return _isValid; }
T val() const { return _v; }
}; Приведённый шаблон обеспечивает половину описания функтора: отображение типов. Он сопоставляет новый тип optional<T> каждому типу T. Теперь опишем его действие над функциями:
template<class A, class B>
std::function<optional<B>(optional<A>)>
fmap(std::function<B(A)> f)
{
return [f](optional<A> opt) {
if (!opt.isValid())
return optional<B>{};
else
return optional<B>{ f(opt.val()) };
};
}Это функция высшего порядка, принимающая функцию как аргумент и возвращающая функцию. А вот другой вариант, без каррирования:
template<class A, class B>
optional<B> fmap(std::function<B(A)> f, optional<A> opt) {
if (!opt.isValid())
return optional<B>{};
else
return optional<B>{ f(opt.val()) };
}С другой стороны, можно реализовать fmap как шаблонный метод optional. Такая неоднозначность в выборе делает абстракцию паттерна "функтор" в С++ проблемой. Должен ли функтор быть интерфейсом, дабы от него наследоваться (к сожалению, шаблонные функции не могут быть виртуальными)? А может быть, свободной шаблонной функцией, каррированной или нет? Сможет ли компилятор С++ корректно вывести недостающие типы, или их надо задавать явно? Представьте, что входная функция f преобразует int в bool. Как компилятор определит тип g:
auto g = fmap(f);особенно, если в будущем появятся множество функторов со своими версиями fmap? (С другими видами функторов мы скоро познакомимся.)
Классы типов
Как же абстракция функтора реализована в Haskell? Используется механизм классов типов. Класс типов задаёт семейство типов, поддерживающих единый интерфейс. К примеру, класс объектов, сравнимых на равенство определяется так:
class Eq a where
(==) :: a -> a -> BoolЗдесь утверждается, что тип a принадлежит классу Eq если он поддерживает оператор (==), который принимает два аргумента типа a и возвращает Bool. Чтобы убедить Haskell что определённый тип относится к Eq, вам понадобится объявить его экземпляром (инстансом, реализацией) класса, и предоставить реализацию (==). Например, имея такое определение точки на плоскости (тип-произведение двух Float):
data Point = Pt Float Floatможно определить равенство точек:
instance Eq Point where
(Pt x y) == (Pt x' y') = x == x' && y == y'Здесь определяемый оператор (==) расположен инфиксно, между двумя образцами (Pt x y) и (Pt x' y'). Тело функции помещается справа от знака =. После того, как Point объявлен экземпляром Eq, можно непосредственно сравнивать точки на равенство. Обратите внимание, что в отличие от C++ или Java вы не обязаны предоставлять класс или даже интерфейс Eq в момент определения Point, — это можно сделать позже. Замечу, что классы типов, — единственный механизм для перегрузки функций (и операторов) в Haskell. Нам он понадобится, чтобы перегружать fmap для разных функторов. Есть одна тонкость: функтор определяется не как тип, а как функция над типами, конструктор типов. Наш класс типов должен описывать семейство конструкторов типов, а не просто типов, как было в случае с Eq. К счастью, механизм классов типов Haskell работает с конструкторами типов также как и с простыми типами (ПП: хороший пример следования функциональной парадигме — даже в мире типов функции ничем не хуже объектов). Ниже определение класса Functor:
class Functor f where
fmap :: (a -> b) -> f a -> f b Оно утверждает, что f есть Functor в том случае, если имеется функция fmap с данной сигнатурой. Здесь f — типовая переменная, того же рода что и типовые переменные a и b. Но компилятор способен понять, что f представляет собой конструктор типов, отслеживая её использование: применение к другим типам, здесь f a и f b. Соответственно, именно конструктор типов мы объявляем экземпляром функтора, как в случае Maybe:
instance Functor Maybe where
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)Замечу, что класс Functor, а также объявления многих общеупотребительных типов включая Maybe его экземплярами, входят в стандартную библиотеку Prelude.
Функторы в C++
Можем ли мы применить тот же подход в C++? Конструктору типов соответствует шаблонный класс, такой как optional, соответственно, нам надо параметризовать fmap дважды шаблонным параметром F. Записывается это так:
template<template<class> F, class A, class B>
F<B> fmap(std::function<B(A)>, F<A>);Но как нам специализировать этот шаблон для разных функторов? К сожалению, частичная специализация шаблонных функций C++ запрещена. Нельзя написать:
template<class A, class B>
optional<B> fmap<optional>(std::function<B(A)> f, optional<A> opt)Вместо этого приходится вернуться к перегрузке функций, в результате мы возвращаемся к первоначальному определению fmap (без каррирования):
template<class A, class B>
optional<B> fmap(std::function<B(A)> f, optional<A> opt)
{
if (!opt.isValid())
return optional<B>{};
else
return optional<B>{ f(opt.val()) };
}Это определение работает, но для правильной перегрузки требуется второй аргумент. Более общее определение fmap просто игнорируется.
Функтор List
Для лучшего понимания значимости функторов в программировании стоит рассмотреть больше примеров. Любой тип, параметризуемый другим типом — кандидат на роль функтора. К примеру, обобщённые контейнеры параметризуются типом своих элементов, рассмотрим список, очень простой контейнер:
data List a = Nil | Cons a (List a)Тут у нас конструктор типов List, представляющий собой отображение любого типа a в тип List a. Чтобы показать, что List есть функтор, нам необходимо определить поднятие функций вдоль функтора. Для заданной функции a->b определим List a -> List b:
fmap :: (a -> b) -> (List a -> List b)Функция, действующая на List должна рассмотреть два случая, соответственно двум конструкторам списка. Случай Nil тривиален, — Nil же и возвращаем, из пустого списка много не выжмешь. Случай Cons хитрее, поскольку затрагивает рекурсию. Подумаем: итак, у нас есть список a, функция f превращающая a в b, и мы хотим получить список b. Очевидно, нужно использовать f, для преобразования каждого элемента списка из a в b. Что именно нужно сделать, если наш (непустой) список определён как Cons головы и хвоста? Применить f к голове и применить поднятое (fmap-нутое) f к хвосту. Это определение рекурсивное, мы определяем поднятое f через поднятое f:
fmap f (Cons x t) = Cons (f x) (fmap f t) Важно, что в правой части fmap f применяется к списку более короткому, чем определяемый нами — а именно к хвосту последнего. Мы применяем рекурсию ко всё более коротким спискам, поэтому неизбежно приходим к пустому списку, или Nil. Но как мы уже определили, fmap f от Nil даёт Nil, тем самым завершая рекурсию. Окончательный результат получаем комбинированием новой головы (f x) с новым хвостом (fmap f t) используя конструктор Cons. В итоге, вот наше объявление списка экземпляром функтора полностью:
instance Functor List where
fmap _ Nil = Nil
fmap f (Cons x t) = Cons (f x) (fmap f t) Если для вас привычнее C++, имеет смысл рассмотреть std::vector, по сути, базовый контейнер C++. Реализация fmap для std::vector — просто обёртка вокруг std::transform:
template<class A, class B>
std::vector<B> fmap(std::function<B(A)> f, std::vector<A> v)
{
std::vector<B> w;
std::transform( std::begin(v)
, std::end(v)
, std::back_inserter(w)
, f);
return w;
}С её помощью мы можем, к примеру, возвести в квадрат ряд чисел:
std::vector<int> v{ 1, 2, 3, 4 };
auto w = fmap([](int i) { return i*i; }, v);
std::copy( std::begin(w)
, std::end(w)
, std::ostream_iterator(std::cout, ", "));Большинство контейнеров C++ по сути функторы. Это обеспечено наличием итераторов, которые можно передать std::transform, — примитивному родственнику fmap. К сожалению, простота функтора теряется под хламом итераторов и временных переменных (как в реализации fmap выше). Из хороших новостей — планируемая к включению в C++ библиотека интервалов (ranges) значительно выявляет их, интервалов, функциональную природу.
Функтор Reader
Теперь, когда мы развили какую-то интуицию, в частности о том, что функторы это своего рода контейнеры, вот вам пример, на первый взгляд выглядящий совершенно иначе. Рассмотрим отображение типа a на тип функций, возвращающих a. Мы ещё не добрались до обсуждения функциональных типов на должном теоретико-категорном уровне, но у нас, как программистов, есть их определённое понимание. В Haskell функциональные типы строятся с помощью конструктора типов — стрелки (->), который принимает два типа: тип аргумента и тип результата. Вы его уже встречали в инфиксной записи, a->b, но с помощью скобок можно ничуть не хуже использовать и префиксную запись:
(->) a bКак и обычные функции, типовые функции нескольких аргументов можно применять частично. И когда мы даём стрелке один аргумент, она всё ещё ждёт другой. То есть,
(->) aпредставляет собой конструктор типов; нужен ещё один тип b чтобы получился полноценный тип a->b. Таким образом, стрелка определяет целое семейство конструкторов типов, параметризованных a. Давайте выясним, является ли оно также семейством функторов. Чтобы не путать два параметра, переименуем их, подчеркнув роли. В соответствии с нашими предыдущими определениями функторов, тип аргумента назовём r, а тип результата a. Итак, наш конструктор берёт любой тип a, и отображает его на тип r->a. Чтобы обосновать функторность, нам надо поднять функцию a->b до функции принимающей r->a и возвращающей r->b. Это типы, создаваемые действием конструктора (->) r на a и b соответственно. Вот такая получается сигнатура fmap:
fmap :: (a -> b) -> (r -> a) -> (r -> b)Получаем своего рода головоломку: имея функции f::a->b и функции g::r->a, создать r->b. Есть только один способ их композиции, и результат как раз такой, как нам надо. Получается такая реализация fmap:
instance Functor ((->) r) where
fmap f g = f . gСработало! Минималист может ещё сократить запись, воспользовавшись префиксной формой:
fmap f g = (.) f gтеперь аргументы можно опустить, получая отождествление двух функций:
fmap = (.)Комбинацию конструктора типов (->) r и такой реализации fmap называют "reader".
Функторы как контейнеры
Мы познакомились с примерами использования функторов в программировании для определения контейнеров общего назначения, или хотя бы объектов, содержащих какие-то значения того типа, которым функтор параметризован. Функтор reader кажется исключением, поскольку мы не думаем о функциях как о данных. Но как мы видели, к функциям применима мемоизация, когда вычисление сводится к поиску в таблице. Таблица это уже данные. С другой стороны, поскольку Haskell ленив, традиционный контейнер вроде списка может на деле реализовываться как функция. Посмотрите, например, на бесконечный список натуральных чисел, который можно описать так:
nats :: [Integer]
nats = [1..]Пара квадратных скобок в первой строке, — встроенный типовый конструктор Haskell для списков. Во второй строке с помощью скобок формируется списковый литерал. Очевидно, подобный бесконечный список в памяти разместить невозможно. Компилятор вместо этого создаёт функцию, которая генерирует Integer-ы по запросу. Haskell фактически размывает границу между кодом и данными: список можно считать функцией, а функцию можно считать таблицей, сопоставляющей аргументам результаты. Это иногда даже практично, при условии, что область определения конечна, и не слишком велика. Но вот реализовать strlen как табличную функцию было бы не практично, поскольку различных строк бесконечно много. Программисты обычно не любят бесконечности, но теория категорий научит вас щёлкать их как орешки. Множество ли это всех возможных строк, или всех состояний вселенной, из прошлого, настоящего или будущего, мы можем работать с этим! Так что я думаю о функторных объектах (объектах типа сконструированного с помощью эндофунктора) как содержащих значения первоначального типа (аргумента функтора), даже если такое значение не представлено физически. Пример функтора в C++, — std::future, который возможно когда-нибудь будет содержать значение, если повезёт; и если вам нужно это значение, возможно, придётся остановиться и подождать, пока другой поток завершит вычисления. Другой пример это объект IO в Haskell, который может содержать введённое пользователем, или будущие версии нашей вселенной с “Hello World!” напечатанным в консоли. При такой интерпретации, функтор есть нечто, способное содержать значение или значения того типа, которым оно параметризовано. Или содержать рецепт создания таких значений. Нас не заботит, можем ли мы посмотреть на это значение, — это не относится к обязательным свойствам функтора. Всё что нас интересует, — возможность манипулировать такими значениями с помощью функций. Если значение было доступно, — мы сможем также увидеть и результат применения функции, если нет, нам достаточно того, чтобы манипуляции подчинялись композиции, а манипуляция с тождественной функцией ничего не меняла. Просто чтобы показать, насколько нам безразличен доступ к значениям внутри функторного объекта, вот вам конструктор, который полностью игнорирует свой аргумент a:
data Const c a = Const cтиповый конструктор Const принимает два типа, c и a. Чтобы создать функтор, нам надо его частично применить, так же, как мы делали с конструктором стрелки (->).
fmap :: (a -> b) -> Const c a -> Const c bПоскольку наш функтор игнорирует свой типовый аргумент, будет естественным в реализации fmap игнорировать функциональный аргумент, — функцию не к чему применять:
instance Functor (Const c) where
fmap _ (Const v) = Const vВ C++ это выглядит немного нагляднее (вот уж не думал, что скажу такое!), за счёт более чёткого различия между типовыми аргументами, которые работают на этапе компиляции, и значениями, работающими во время выполнения.
template<class C, class A>
struct Const {
Const(C v) : _v(v) {}
C _v;
};C++ -реализация fmap также игнорирует функциональный аргумент, и по сути преобразует тип Const, не трогая значение.
template<class C, class A, class B>
Const<C, B> fmap(std::function<B(A)> f, Const<C, A> c) {
return Const<C, B>{c._v};
}Несмотря на странный вид, функтор Const играет важную роль во многих построениях. В теории категорий это частный случай функтора Δc, упомянутого ранее — эндофункторной разновидности чёрной дыры. В будущем мы познакомимся с ним поближе.
Композиция функторов
Несложно убедиться, что для функторов между категориями композиция работает точно также, как для функций между множествами. Композиция двух функторов, при действии на объекты, есть просто композиция соответствующих отображений объектов, аналогичная ситуация с действием на морфизмы. После прыжка вдоль двух функторов, единичные морфизмы остаются единичными, также как и композиция морфизмов остаётся таковой для образов. Ничего особенного. В частности, легко сочетаются эндофункторы. Помните функцию maybeTail (ПП: из предыдущей главы)? Давайте её перепишем, применительно к стандартным спискам Haskell:
maybeTail :: [a] -> Maybe [a]
maybeTail [] = Nothing
maybeTail (x:xs) = Just xs(Конструктор пустого списка, который мы обозначили Nil заменён пустой парой квадратных скобок []. Конструктор Cons заменён инфиксным оператором : (двоеточие).) Результат maybeTail имеет тип композиции двух функторов, Maybe и [], действующих на a. Каждый из этих функторов снабжён собственной версией fmap, но что если мы хотим применить некоторую функцию f к содержимому композиции: Maybe list? Необходимо пролезть сквозь два слоя функторов. Используя fmap можно пройти сквозь внешний, Maybe. Но мы не можем отправить f внутрь Maybe, поскольку f не работает со списками. Нам нужно послать (fmap f), для действия на внутренний список. Например, давайте возведём в квадрат элементы Maybe list целых чисел:
square x = x * x
mis :: Maybe [Int]
mis = Just [1, 2, 3]
mis2 = fmap (fmap square) misКомпилятор, проанализировав типы выяснит, что для внешнего fmap следует использовать реализацию из экземпляра Maybe, а для внутреннего, — реализацию от функтора list. Возможно, не совсем очевидно, что код выше можно переписать так:
mis2 = (fmap . fmap) square misНо вспомните, что о fmap можно думать как о функции единственного аргумента:
fmap :: (a -> b) -> (f a -> f b)В нашем случае, второй fmap в (fmap . fmap) принимает на вход
square :: Int -> Intи возвращает функцию типа
[Int] -> [Int]Затем первый fmap берёт получившуюся функцию и в свою очередь возвращает
Maybe [Int] -> Maybe [Int]И наконец эта функция применяется к mis. Таким образом, композиция двух функторов это функтор, чей fmap есть композиция соответствующих fmap. Возвращаясь к теории категорий: достаточно очевидно, что композиция функторов ассоциативна (и отображение объектов ассоциативно, и отображение функторов). Кроме того, в каждой категории имеется единичный функтор, который отображает каждый объект в него же, и аналогично действует с морфизмами. То есть, функторы имеют все необходимые свойства морфизмов некоторой категории. Но что это будет за категория? Это должна быть категория, в которой объекты это категории, а морфизмы это функторы. Это категория категорий. Но категория всех категорий должна включать себя также, что ведёт появлению парадоксов того же типа, что делают множество всех множеств невозможным. Однако, существует категория всех малых категорий Cat (которая велика, и соответственно своим членом не является). "Малая" это такая категория, объекты которой составляют множество, в противоположность чему-то, большему, чем множество. Заметьте, что в теории категорий даже бесконечное несчётное множество считается "малым". Наверное, я рассказываю вам всё это, поскольку считаю поразительным, как одни и те же структуры повторяются на разных уровнях абстракции. Позже мы увидим, что функторы тоже составляют категорию.
Упражнения
- Можно ли превратить типовый конструктор `Maybe` в функтор, определив
fmap _ _ = Nothing
который игнорирует оба своих аргумента? (Подсказка: проверьте функторные законы) - Докажите функторные законы для функтора `reader` (Подсказка: там всё просто).
- Реализуйте функтор reader на вашем втором любимом языке (первый, естественно, Haskell).
- Докажите законы функторов для списка. Начните с допущения, что законы выполняются для хвостовой части списка (то есть используйте индукцию).
Благодарности
Гершом Базерман любезно продолжает рецензирование текста. Автор благодарен ему за терпение и высказанные идеи.
leshabirukov: приблизительно первая половина главы переведена совместно мною и Bodigrim, который также участвовал в редактировании окончательной версии. Несогласованность нашего труда лежит на моей совести.
Автор: leshabirukov