В прошлых статьях я затрагивал тему простых рейтингов. В комментариях меня попросили расписать тему рейтингов, которые выдают для каждого пользователя свои.
Нам нужно используя оценки других пользователей предсказать оценку фильма для текущего пользователя. Т.е. наша задача сводится к прогнозированию оценок конкретного пользователя.
Введение
Пользователя на основе которого считаются оценки мы назовем критиком
Пользователя для которого мы будем считать оценку мы будем называть пользователем.
Хотя пользователи и критики находятся в одной базе и пересекаются нам удобнее называть их по разному. Если у пользователя есть один голос, то мы можем что-то предсказать. Но критик с одним голосом бесполезен. Также можно добавить в качестве критика средний рейтинг фильмов или рейтинг по IMDB и кинопоиску.
Мы считаем что средняя оценка любого фильма статистически достоверна (у фильма много голосов), как средняя оценка любого критика (критик много раз голосовал). Мы можем прогнозировать эти два значения и часть критиков и фильмов с малым числом оценок убрать из рейтинга.
Мы будем считать что все оценки по 10ти бальной шкале от 1 до 10. Для любой шкалы это верно, хотя чем больше в ней вариантов оценок — тем лучше. Однако для оценок ± у меня есть сомнения что она будет работать. Для оценок «мне нравится» или «покупки» метод будет работать, однако, есть другие варианты.
Выбор лучшего критика
Начнем с простого примера. Мы каждую субботу ходим в кино. Однако, чтобы не ходить на кота в мешке мы предварительно читаем колонку кинокритики в 5-6 газетах. В последнее время нам лень читать 5 газет и нам нужно выбрать одну, оценки кинокритика которой максимально похожи на ваши. Т.е. ваши вкусы и вкусы кинокритика максимально совпадают.
Например, вот таблица двух кинокритиков
Ваши оценки:| 5 | 8 | 7 Кинокритик 1:| 5 | 8 | 4 Кинокритик 2:| 4 | 6 | 8
У первого кинокритика все оценки совпадают, кроме одной. Но эта оценка сильно отличается. У другого все оценки немного отличаются. Вопрос кто из них ближе.
Вопрос как получить численную оценку близости вкуса критика и вашу? Есть бесконечно много метрик, которые это определяют. Две самые простые это Эвклидова (расстояние между двумя точками из школьной программы) и Манхэттенова (в честь района Нью-Йорка).
Эвклид против Манхэттена
Манхэттенова метрика названа так потому-что отражает расстояние, которое нужно пройти в крупном городе с перпендикулярными улицами, когда можно двигаться только параллельно осям координат.
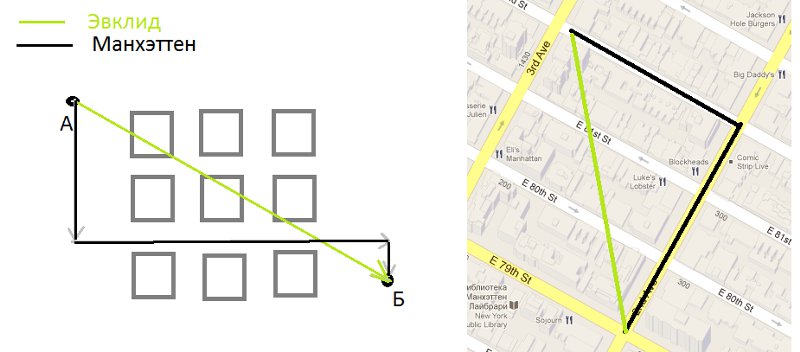

Если посчитать Манхэттен:
Кинокритик 1: /5-5/+/8-8/+/7-4/=3
Кинокритик 2: /5-4/+/8-6/+/7-8/=4
Первый лучше
Если посчитать Эвклида
Кинокритик 1: (5-5)^2+(8-8)^2+(7-4)^2=9
Кинокритик 2: (5-4)^2+(8-6)^2+(7-8)^2=6
Второй лучше. Корень я не брал, но неравенство сохранится независимо от того взять его или нет.
Метрики отражают расстояние на многомерном пространстве. В математике метрику считают характеристикой пространства, которая как бы задана. И какая из них лучше философский вопрос. С философской точки зрения, чем проще гипотеза, тем вероятнее что она правильна. С этой точки Эвклид лучше — он не предполагает каких-то препятствий, которые мешают двигаться не параллельно координатной оси. Квадрат гладкая функция и является частным случаем умножения, которое в свою очередь является частным случаем суммирования. А модуль — условная функция. Более того существует метод наименьших квадратом, с помощью которого даже открыли планету Цереру.
Если рассуждать на практике, то не все так однозначно. Квадрат увеличивает значимость одиночных сильных сдвигов, как с последним фильмом в таблице. Это с одной стороны хорошо — большие сдвиги более показательны. Однако, увеличивают значимость случайных ошибок, как пользователя так и критика.

Расстоянием между пользователем и критиком будет расстоянием между их оценками за одинаковые фильмы. Поскольку, у разных критиков разное число фильма за которые и критик и пользователь проголосовал, то нужно делить на сумму совпадений это назовем средним расстоянием. Также, поскольку существуют статистические погрешности, мы заменим среднее расстояние его прогнозом (далее ПСР).

D большое среднее расстояние всех оценок критиков от всех оценок пользователей (можно заменить константой) — им мы замещаем недостоверную часть расстояния. f(n) — оценка недостоверной части расстояния. 0.5/sqrt(n) в самом простом случае.
Смелость и снобизм
Другая проблема Эвклида, то что он наказывает за смелость. Чем меньший разброс средней оценки у критика, тем больше шансов, что случайный пользователь выберет этого критика. Например, если средняя оценка по сайту 5, то критик голосующий только пятерками получит больше всего пользователей. А критик голосующий равномерно 1 и 9 получит меньше всего пользователей. Стоит ли балансировать критиков так, чтобы вне зависимости от смелости они получали равный шанс на пользователя — нужно смотреть на практике.
Можно считать снобизм (среднее расстояние между оценкой пользователя и средней оценкой фильма) пользователей и критиков и учитывать это при поиске критика. В самом простом варианте добавить пользователю и критику виртуальный фильм «снобизм».
Вариант с несколькими критиками
Он решается аналогично. Вопрос в том, как сбалансировать их оценки. Можно посчитать средневзвешенное по ним и пускай каждый из них будет иметь коэффициент обратно пропорциональный его ПСР. Вот формула прогноза оценки, которую даст пользователь фильму.

di c точкой прогноз расстояния от пользователя до критика. Ri — оценка критиком этого фильма.
Как вы видите ничего сложного в теории нет — проблемы возникнут на практике, когда нужно все это оптимизировать по скорости и подстраивать рейтинг.
Автор: Hkey






