Введение
Промышленность не стоит на месте. Еще в 1990 году псевдослучайные числа, длинной в целых 40 бит, сгенерированные на ЭВМ можно было угадать за несколько часов [1]. На сегодняшний же день, качественные характеристики псевдослучайных величин на ЭВМ поражает даже опытных математиков. Во многих областях применения алгоритмов генераций всевдослучайных чисел существует ряд ограничений, связанных с тем или иным недостатком методов их генерации. Совершенствованию существующих методов способствует высокий интерес к теме, который повышается с ростом числа публикаций. Пусть эта статья станет моим вкладом в развитие методов моделирования и генерации случайных процессов, так важных для моих исследований и разработок.
Предыстория
Краткий экскурс в историю методов генерации случайных чисел показывает, что в погоне за стохастичностью разработчики готовы были идти на крайние меры. Так в 1996 году был изобретен и запущен источник случайных чисел под названием Lavarand. Метод генерации чисел был сведен к обработке фотографии декоративного светильника – лавовой лампы, которая непрерывно меняла свой облик непредсказуемым образом [2]. Также стоит упомянуть и о первых генераторах случайных величин на обычных ЭВМ. Разработала их фирма Intel в 1999 году, и назывался данный компонент Firmware Hub. Метод генерации заключался в регистрации теплового шума резисторов с последующим усилением и использованием в качестве управляющего сигнала осциллятора, регулярно меняющего своё значением между “0” и “1” [3].Такая система работала непрерывно, вне зависимости от нужды пользователя в использовании системы генерации случайных чисел.
Главная проблема генерации истинно случайных чисел остается обязательное наличие аналоговой составляющей, так как качественные характеристики цифровых методов генерации псевдослучайных чисел не удовлетворяют многим стандартам National Institute of Standards and Technology, а на практике абсолютно не годятся для решения многих задач прикладного характера, например криптографии.
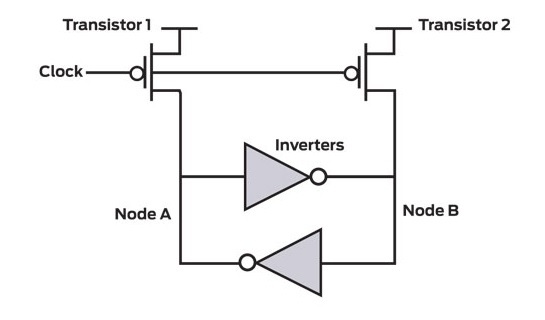
Рис.1 Схема генератора случайных чисел.
В апреле 2012 года в продажу поступили первые процессоры с микроархитектурой под кодовым названием “Ivy Bridge”. Особенностью этой архитектуры стало наличие генератора, позволяющего использовать аналоговые тепловые шумы напрямую для генерации случайных чисел [4]. На рис.1 представлена схема такого генератора. На первый взгляд она слишком идеализирована, ведь равновероятного появления “0” или “1” можно добиться только при абсолютной идентичности инверторов, чего на практике добиться невозможно. Поэтому неравномерность генерируемых чисел требуется компенсировать, что и делается в постобработке.
Генерация случайных чисел с равномерным законом распределения
Пожалуй, самым важными и незаменимыми методами моделирования случайных процессов, являются методы генерации равновероятных случайных величин, так как большая часть алгоритмов моделирования случайных процессов с произвольным законом распределения базируются именно на них [5].
Самыми популярными способами получения равномерно распределенных случайных величин являются:
• Таблицы случайных чисел
• Физические генераторы случайных чисел (такие как Firmware Hub или генератор случайных чисел в “ Ivy Bridge ”)
• С помощью цифровых генераторов или датчиков, с использованием формул.
Надо сказать, что в последнем пункте результатом генерации являются псевдослучайные числа. Как бы ни парадоксально звучало следующее утверждение, но главным недостатком таких чисел – это то, что в большинстве случаев их нетрудно предсказать, а в некоторых алгоритмах генерации их последовательность ещё и имеет свойство периодически повторятся. В некоторых прикладных задачах это недопустимо, но, несмотря на это, именно эти способы генерации случайных величин с равномерным законом распределения получили наибольшее распространение, ввиду простоты их реализации на ЦЭВМ.
Среди них наиболее популярными считают:
• Конгруэнтные методы.
• Методы, основанные на использовании регистра сдвига с линейной обратной связью (LFSR).
Линейный конгруэнтный метод по сей день используется для генерации случайных чисел в самых популярных средах программирования, таких как MSVS [6], MSVB [7], Java [6], Borland C/C++ [6], GCC [8] и других. Распространенность этого метода говорит о его эффективности.
Суть методов этого класса заключается в вычислении последовательности случайных чисел Y(n):
Y(n+1) = (x*Y(n) + c) % m,
где m – количество значений из которых формируется последовательность (m ≥ 2), % — остаток от деления, x – множитель (0 ≤ x < m), с – приращение (0 ≤ с < m), Y(0) – начальное значение (0 ≤ Y(0) < m) [9].
От выбора чисел m, x, c, Y(0) зависят качественные параметры стохастичности полученных чисел.
Пожалуй, самым универсальным в использовании, является класс методов, использующих сдвиговые регистры. Они незаменимы, как в задачах криптографии [10] (GSM, Bluetooth) так и тестирования цифровых устройств [11]. Имеются упоминания использования одного из таких алгоритмов в качестве делителя тактовой частоты или счётчика [12]. Также алгоритмы с использованием сдвигового регистра используются в задачах скремблирования [13].
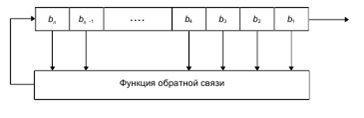
Рис.2 Схема регистра сдвига с обратной связью
Простейшая реализация этого алгоритма представлена на рис.2. После задания начального состояния регистра сдвига, из него каждый такт происходит считывание всевдослучайного бита. Затем над числом происходит некоторые, зависящие от конкретной реализации, математические операции, результат которых записывается после сдвига в “освободившийся” бит регистра.
Заключение
Разумеется, рассмотрены далеко не все, методы генерации случайных чисел. Но именно они повсеместно применяются в различных задачах, будь то моделирование стохастических нестационарных процессов для синтеза алгоритмов определения угла низколетящей цели или криптография и скремблинг кодовой последовательности. Ввиду наличия возможности просчитывать результаты работы таких алгоритмов, не зная входных данных, пусть и с затратой значительных ресурсов, вопрос их доработки весьма актуален.
Список использованных источников:
[1] Goldberg, I. Randomness and the Netscape Browser / I. Goldberg, D. Wagner // Dr. Dobb’s Journal. – 1996. – January, P.66-70.
[2] Патент US № 7031991 B2 Hadamard-transform on-line randomness test / Laszlo Hars 17 apr. 2002.
[3] Jun, B. The Intel Random Number Generator / B. Jun, P. Kocher // Cryptography Research Inc. white paper, 1999.
[4] Как работает новый генератор случайных чисел Intel
[5] Монаков, А. А. Основы математического моделирования радиотехнических систем: учеб. пособие / А. А. Монаков; ГУАП. СПб., 2005. 15 с.
[6] ISO/IEC 9899:201x Last public Committee Draft from April 12, 2011, page 346f.
[7] How Visual Basic Generates Pseudo-Random Numbers for the RND Function. Microsoft Support. Microsoft
[8] GNU Scientific Library: Other random number generators
[9] Дональд Кнут. Том 2. Получисленные методы // Искусство программирования. Указ. соч. — С. 21—37.
[10] Barklan E., Biham E., Keller N. Instant ciphertext-only cryptanalysis of GSM encrypted communication. — Journal of cryptology №21-3, 2008.
[11] Ларин, А. Л. Основы цифровой электроники: учебное пособие / А.Л. Ларин; М.: МФТИ, 2008. — 314 с. — ISBN 978-5-7417-0228-4.
[12] Efficient Shift Registers, LFSR Counters and Long Pseudo-Random Sequence Generators
[13] Варгаузин, В. Принципы цифрового телевидения стандарта ATSC / В. Варгаузин — Журнал Теле-Спутник №9(47), 1999.
Автор: mcBottle






