Одна из проблем современного интернета — слежка и несанкционированный доступ к пользовательским данным. Оборотная сторона этого являния, о которой вспоминают несколько реже — несанкционированное ограничение доступа к данным. Или, попросту, цензура.
О ней и предлагается сегодня поговорить. Количественно исследовать, как она работает в зависимости от сложности поступающей информации, и понять, что и насколько сквозь неё всё-таки проходит.
Интуитивное описание задачи
Итак, предположим, поток информации к Вам перекрывает некий фильтр. Пытающийся отсекать всё, что ему не нравится. Фильтр пассивный — то есть, сам не усиливающий никаких сигналов, а только подавляющий неугодные.
Жизненные примеры многочисленны и показывают, что цензура, вообще-то — не всегда зло:
- Антивирус. Одна вычислительная система на входе частично эмулирует поведение потенциально исполняемого кода в попытках распознать его возможную вредоносность. Другая, похожая, система этот код исполняет — и может пасть жертвой атаки, если антивирус ошибся, а другой защиты нет.
- Блокировка сайтов. Одна группа людей вычитывает содержимое интернета и принимает решение, какие сайты заблокировать. Люди из другой группы тоже читают инернет, в том числе и запрещённые сайты. Если содержимое последних достаточно иносказательно, то их мысль может быть понята адресатом, хотя и пропущена цензурой.
- Википедия (и любой публичный форум). Здесь цензором являются сами же читатели; мысли или статьи, полагающиеся неверными, просто редактируются.
- Сообщения начальства в любой достаточно крупной конторе с количеством «слоёв» L >> 1.
- И даже светофильтр на фотоаппарате. Отсекая одни длины волн, он позволяет другим достигать матрицы камеры и формировать полезное нам изображение.
Эффективность цензуры зависит от сложности поданной информации. Сообщения простые засечь и отсечь легко. Сообщения нетривиальные имеют больше шансов проскользнуть сквозь фильтр.
К примеру, допустим, кто-то решил запретить пропаганду Теоремы Пифагора в сети. Можно вообразить следующие уровни сложности этой пропаганды:
1. «Пифагор гений, а вы все и%%%ты!» — низкая сложность. Не содержит ничего, кроме уверенности и эмоций. Для понимания такого аргумента достаточно умения читать. Сразу отметим: речь вовсе не идёт о согласии с аргументом или его верности. Мы говорим только о понимании.
Распознать и заблокировать подобный аргумент довольно просто.
2. «Формулы, связывающие длины сторон прямоугольных треугольников, применяется при строительстве мостов, зданий, изготовлении машин, в картографии и прокладке маршрутов самолётов». Это уже сложнее. Апелляция идёт к отраслям современной индустрии и к геометрии. Требуется хотя бы знать об их наличии. Это класс так 7-й школы. Посылка к выводу скрыта: "… а поскольку все эти индустрии работают, то Теорема Пифагора — тоже" — и требует некоторой концентрации ума от цензора. Особенно учитывая, что сама теорема тоже явно не упомянута.
3. Приводится чертёж редкого доказательства теоремы (например, [10]), желательно в декоративной форме. От читателя требуется медитативное вглядывание в рисунок и владение геометрией, чтобы самому внезапно прийти к правильному выводу. И хотя в школе эту теорему и проходят, на практике редко кто помимо поступающих в технический ВУЗ готов добровольно повторить её доказательство.
4. Можно вообразить что-нибудь ещё. Скажем, как строка «huxj5lh» может быть связана с теоремой Пифагора?
Так вот. Оказывается, о пропускной способности пассивой цензуры можно сделать несколько математически точных количественных выводов, верных при весьма широких допущениях. Перечислим их:
Первое и главное: цензор и приёмник — сущности одного класса. Например, люди и люди. То есть, фильтр можно представить в виде набора тех же приёмников, только ориентированных не на восприятие, а на подавление информации.
Второе: приёмник и фильтр одинаково монотонно воспринимают сложность входящей информации. То есть, если A сложнее, чем B, для Вас, то в том же порядке расположена сложность и для цензуры.
Третье: цензура гораздо мощнее, «толще», чем приёмник.
При этих допущениях можно утверждать, что максимум Вашей способности улавливать просочившуюся сквозь «толстую» пассивную цензуру информацию находится на таком уровне её сложности, где пропускная способность цензуры составляет 37%
Кому интересно — доказательство ниже. Кому нет, переходите к разделу с выводами и примерами.
Математическое описание
Понятно, что эффективность восприятия за слоем цензуры зависит от сложности сообщений. Слишком простая информация легко фильтруется и адресата не достигает. Слишком сложная не распознаётся и проходит насквозь — но, к сожалению, она слишком сложна и для слушателя, чтобы понять и заметить. Значит, пик способности улавливать ошибочно пропущенную цензурой информацию должен находиться где-то в области «промежуточной» сложности. Вопрос: где именно?
Пусть x обозначает сложность приходящего пакета информации. S(x) — «чувствительность» цензуры к пакетам определённой сложности, выраженная как вероятность эту информацию засечь и отсечь. Эта чувствительность строго убывающая, выглядит она как-то так:
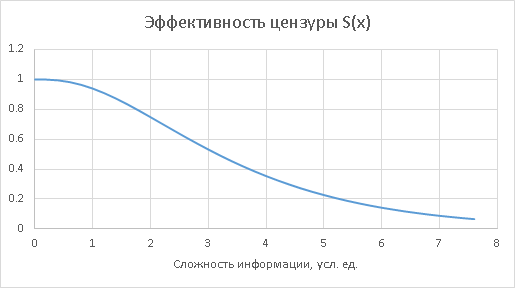
Тогда «пропускающая» способность цензуры есть, очевидно, 1-S(x):
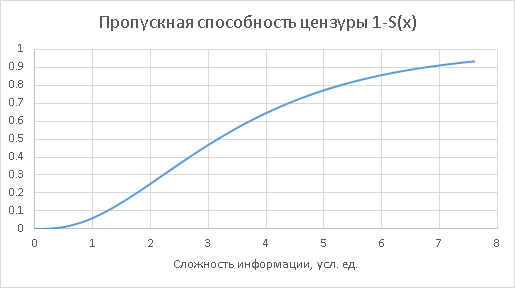
Всё, что прошло, попадает к Вам. Ваша чувствительность есть Q(x) — вероятно, с порогом ниже, чем у цензуры. Качественно как-то:
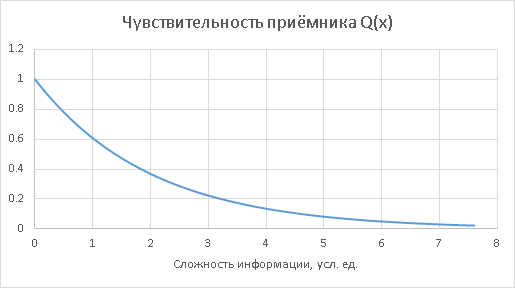
Тот сигнал, который Вы всё-таки расслышите, есть произведение того, что прошло, на то, что можно услышать, т.е. Q(x)*(1-S(x)):
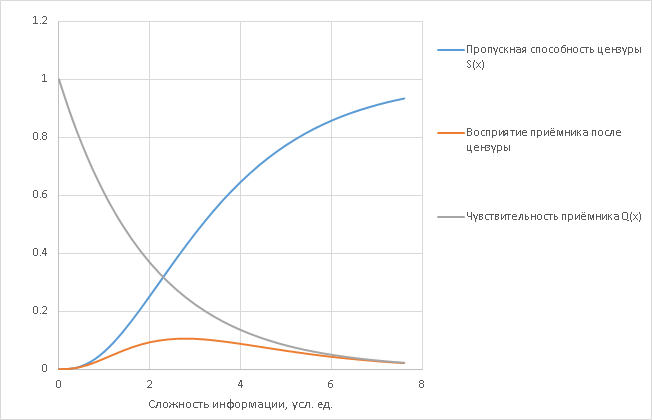
До этого места всё абстрактно. Теперь вспомним главное допущение: что цензуру осуществляют элементы того же типа, что и приёмники. Поэтому её можно мысленно представить как набор N >> 1 фильтрующих элементов, действующих более-менее независимо (если они зависимы, надо просто представить каждую синхронизованную группу как отдельный детектор, изменив эффективную величину N).
Пусть чувствительность каждого элемента цензуры есть s(x) — то есть, с такой вероятностью её работник засекает, что через него пытается проскользнуть «неправильная» информация. Соответственно, с вероятностью 1-s(x) он этого не замечает, пропуская пакет. Если элементов N, то вероятность, что все они пакет прохлопают, составляет (1-s(x))N.
Поскольку Вы — тоже человек со способностями, похожими на способности работников цензуры, то Ваша чувствительность приблизительно равна чувствительности её работника, т.е. Q(x) ≈ s(x).
Перемножив, получаем величину потока информации, которую Вы всё-таки воспринимаете:
I(x) ≈ s(x)*(1-s(x))N
Давайте найдём его максимум. Для этого надо продифференциировать это выражение по x и насильственно приравнять нулю:
0 = ∂I(x)/∂x = (∂I(s)/∂s)*(∂s/∂x) = (∂s/∂x)*[(1-s(x))N — N*s*(1-s(x))N-1] = 0.
Т.к. s(x) монотонна (допущение 2), её производную можно сократить. Равно как и величину (1-s(x))N-1. Остаётся:
(1-s) — sN = 0, или
s* = 1/(N+1)
То есть, максимум восприятия информации будет на том уровне её сложности, где Ваша воспринимающая способность составляет 1/(N+1). Какова фильтрующая способность цензуры на этом уровне? Подставим s* в (1- s(x))N, получим:
S* = S(x|s(x)=s*) = (1-1/(N+1))N
С ростом N это выражение очень быстро стремится к… золотому пределу, равному попросту 1/e, или 37%! С приличной точностью это происходит уже при N порядка 3-4:
| N | S* |
| 1 | 0.50 |
| 2 | 0.44 |
| 3 | 0.42 |
| 4 | 0.41 |
| 5 | 0.40 |
| 10 | 0.38 |
Итак, максимум Вашего восприятия за мощным слоем пассивной цензуры находится там, где её пропускная способность составляет 37%. А поскольку ответ очень слабо зависит от «толщины» цензуры N, то он остаётся верным при довольно далёких отклонениях от модели. Всякий фильтр, который можно хотя бы приблизительно представить в виде набора независимых приёмников с достаточно большим их числом N, будет удовлетворять этому выводу.
Важно лишь, чтобы сложность информации оставалась «одномерной» и монотонной. Без сообщений, которые для Вас тривиальны, а для цензуры очень сложны и она их насквозь пропускает (или наоборот).
Практическое применение
Итак, максимум уловительной способности «за цензурой» приходится на тот уровень сложности сигнала, при котором она пропускает 37% фактов.
Какая от этого знания может быть польза?
Ну, во-первых, если Вам удалось уловить один прорвавшийся сквозь фильтрацию пакет, то полезно и приятно знать: на самом деле подобных пакетов было послано 2-3. И ещё в N+1 раз больше пакетов примитивных, но полностью подавленных. Мир сбалансирован существенно иначе, чем видно сквозь фильтрацию.
А во-вторых, этим можно пользоваться для её обнаружения. Способ дорогой и медленный, но лучше, чем ничего. Работает так.
Положим, на некоторый вопрос есть две точки зрения A и B. A — «разрешённая», цензурой пропускаемая на 100% независимо от уровня сложности. И B, запрещённая, фильтруемая. На входе у Вас большой набор высказываний {F}, говорящих как за A, так и за B. Можно ли по их соотношению понять, фильтруется ли что-то, и если да, то что именно?
Отсортируем высказывания F по сложности для восприятия x. Разумеется, субъективно, тут других вариантов нет. Как умеем. Но стараясь аккуратно. Простые налево, сложные направо, остальные где-то между ними примерно в порядке возрастания. Получилась последовательность F(x). А теперь смотрим, как распределена доля точек зрения A и B в зависимости от сложности.
A не цензурируется, т.е. доходит до нас насквозь на любом уровне сложности, который мы ещё воспринимаем. В предположении, что цензур не больше одной, количество сообщений A(x) будет константой.
Радикально иначе будет вести себя B(x). В области самых простых сообщений вариантов за B почти не будет (их все отфильтровали!) Потом их число начнёт расти, пока не достигнет константы, характеризующей «нефильтрованное» соотношение мнений.
Если нарисовать пропорции A/(A+B) и B/(A+B) как функции x, то при наличии цензуры будет ожидаться примерно такая картинка:
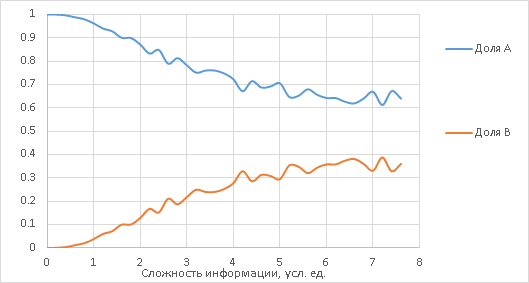
Когда графики примерно таковы, то с некоторыми основаниями можно предполагать, что а) действует пассивная цензура, и: б) ею подавляется именно вариант B.
А если график выглядит так?
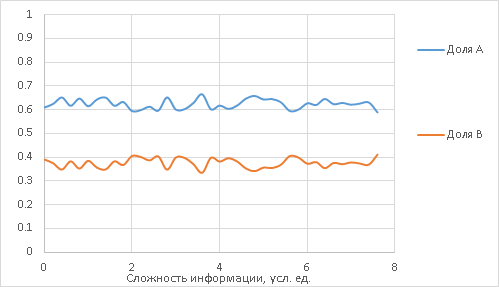
Тогда, скорее всего, никакой цензуры нет. Или мы недостаточно умны, чтобы её заметить. Ну или она не пассивная, на что нужны совсем другие методы.
Важно повторить, что в данном случае никто не говорит, будто вариант B — истина. Правдой вполне может быть как раз и официальный вариант A. Истину от лжи отличать — задача куда большей сложности. Наша цель проще: понять, в какую сторону нам «подгибают» картинку. И только.
Тестирование метода
Попробуем применить то, что мы здесь насчитали, на практике.
Тест 1 (самый простой): фотография. Вот у меня в руке лист кремния (Si) толщиной 0.7 мм:

Что получится, если использовать его в качестве светофильтра для цифровой камеры с удалённым внутренним ИК-фильтром? Приёмник — фактически кремний, 15 микрон. И фильтр — кремний. Тот же материал, только толще, 700 микрон. В качестве «сложности» выступает длина волны света. Теория предсказывает, что максимум чувствительности такой системы будет приходиться на ту длину волны, при которой входной фильтр пропускает 37% излучения. Смотрим на график прозрачности кремния от длины волны (с [20]).
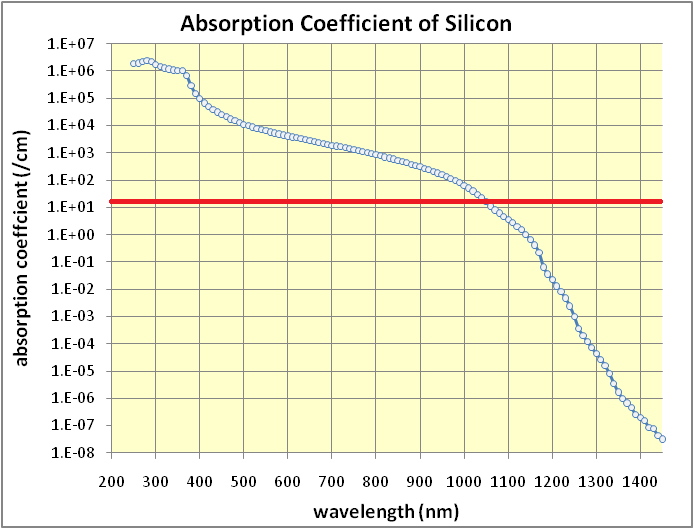
Я провёл на нём красную линию, соответствующую обратной толщине 1/0.07 см. Там, где она пересекает кривую пропускания кремния, прозрачность фильтра составляет e-1 = 37%. Это происходит на длине волны 1050 нм. Значит, там же должен находиться максимум чувствительности камеры с таким фильтром. Спектрографа у меня нет, но это можно косвенно-приблизительно проверить другим способом. Фотографируем через кремний бутылку воды:

Вода тёмная. Почему? Потому что на 1050 мкм её эффективное пропускание падает до ~5 сантиметров ([30]). Для сравнения, на 800 нм и уж конечно в видимом свете всё совсем не так:


Значит, пик восприятия такой камеры — действительно где-то в районе 1000-1100 мкм. Как и ожидалось.
Второй пример, более интересный. Вот вроде бы нейтральный ролик про распределение профессий между республиканцами и демократами в США: www.youtube.com/watch?v=R34rXt_q2sY. Разумеется, у него куча комментариев как за, так и против каждой из партий. Комментарии по сложности можно разбить на три уровня:
- Низкий. Требует только умения читать, аппелирует не более чем к эмоциям («все XXX — ко%%ы!!!»).
- Средний. Требует каких-то знаний по школьной программе, пытается апеллировать к фактам и логике (далеко не всегда корректно и далеко не всегда к верным фактам, но всё-таки пытается).
- Высокий. Требует хорошего знания истории, политики, экономики США и/или мира. Использует нетривиальные логические посылки.
Чего ожидает теория? Республиканская и демократическая партии примерно равны по силе. Даже при желании им вряд ли удастся серьёзно подавить противную сторону на широко видимом общественности ролике. Соответственно, аргументы «за» и «против» каждой партии должны быть представлены примерно равномерно по всему воспринимаемому мною спектру сложности. Берём эксель, тратим три часа на вычитывание комментариев, и — результат:
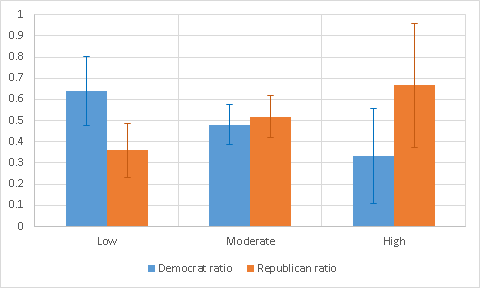
Лёгкий перекосик в сторону более «тупых» аргументов от демократов наблюдается, но в целом разница лежит в пределах статистического шума. Серьёзных указаний на присутствие цензуры не обнаружено, по крайней мере, в пределах спектра сложности, доступного моему личному интеллекту.
Возьмём более интересный пример №3: «летали ли американцы на Луну?» Ютюб — наше всё, вот ролик, где утверждается, что лунные высадки — сплошной обман: www.youtube.com/watch?v=vPRyo4cSESQ. Снова сортируем комментарии по сложности (меня хватило штук на 80):
- Эмоции и наезды
- Требуется 6-8 классов хотя бы на «тройку».
- Без университета или специальности не разобраться.
Результат. (Pro — что американцы на Луне всё-таки были, Con — что нет):
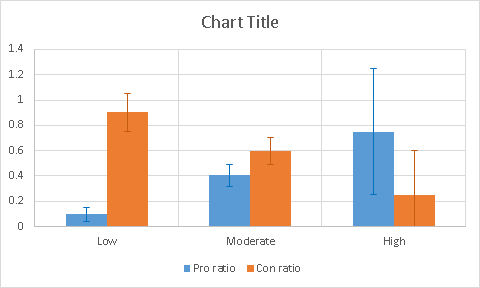
Оч-чень интересно! Аргументы «ты, ко%ёл!» доминируют среди полагающих лунные экспедиции обманом. С увеличением сложности («а как же космическая радиация?») их пропорция заметно уменьшается. К сожалению, комментариев высокой сложности слишком мало, такова уж аудитория ютюба. Но даже по двум точкам складывается весомое впечатление, что высказывания за реальность полётов на Луну в данном ролике цензурируются. Делает ли это сам автор? Допустимо. Но куда более вероятным представляется другое объяснение: люди, не воспринимающие всерьёз Moon hoax, просто не пользуются грубыми и необоснованными «аргументами». Своего рода внутренняя, субкультурно обусловленная цензура. А, между прочим, зря. Рассуждения про лазерные дальномеры их оппонентам до лампочки из-за непонятности. А вот простое «в нашей школе только %%%%ы ещё верят в Moon Hoax» может оказаться более действенным :))
Заключение
Итак, пассивная цензура, в принципе, обнаружима. Максимум возможности что-то расслышать сквозь неё приходится на тот уровень сложности сообщений, где её пропускная способность составляет 37%. Количественно расчерчивая кривые пропускания как функции сложности поступающей информации, можно делать практические выводы о наличии и силе цензуры.
Разумеется, описанный способ обладает массой недостатков. Он субъективно зависим, он может дать ошибочные результаты при отклонениях от модели. Наконец, важно помнить, что он — вовсе не быстрый и не дешёвый. Даже на промерку кривой пропускания в двух точках со скромной точностью в 20% при 1σ достоверности требуется, при самом оптимистичном раскладе, порядка 50 сообщений. Каждое из которых надо прочитать, понять, соотнести со стороной в дискуссии и, главное, оценить уровень сложности. Сделав это обязательно вручную, если Вас интересует цензура человеческая, а не автоматическая. Это пара часов времени.
Так что способ требует труда и терпения. Но если кому-то всё-таки покажется полезным или интересным — что ж, значит, время потрачено не зря.
Спасибо,
Евгений
Автор: eugeneb0



