Идея написать популярно про большие числа пришла во время чтения этой статьи. Речь в ней шла о числах-гигантах, имеющих хоть какой-то физический смысл. И заканчивается она упоминанием числа Грэма. Того числа, которое будет точкой отсчета сегодняшней статьи. Чтобы представить себе масштабы бедствия я настоятельно рекомендую предварительно прочитать вот эту статью, в которое объясняется о числе Грэма на пальцахTM — там автор очень красочно и последовательно рассказывает о границах восприятия, в которые мы себя зажимаем, когда говорим о больших числах.
Для начала, чтобы предотвратить возможные комментарии в стиле «а нафига оно надо, это ведь всё равно не имеет ровным счетом никакого практического смысла» — ответ в
В общем, как сказал IngvarrT в обсуждении статьи про числа-гиганты, весь дальнейший текст сводится к фразе «Прикиньте, шо придумали математики».
Для начала необходимо прояснить, что когда мы говорим о больших числах (даже не БОЛЬШИХ, а просто больших), то как правило имеем ввиду не последовательность цифр, образующих это число, а способ (или метод), с помощью которого данное число получается. Конечно, мы можем написать секстиллион как 1000000000000000000000, но все же привычнее видеть 1021. В данном случае способом описания числа будет операция возведение в степень (которая выглядит как запись числа верхним индексом справа). Использование подобных способов позволяет сократить запись числа, оставляя лишь способ его образования (чего, разумеется, вполне достаточно для совершения математических действий над ним). Так мы логически подошли к тому, что все разговоры в БОЛЬШИХ числах сводятся к поиску максимально компактной записи максимально большого числа. Итак, «шо же придумали эти математики».
Все мы знаем три основные арифметические операции: сложение (a+b), умножение (a × b), возведение в степень (ab). Никогда не задумывались, что все эти операции последовательно вытекают одна из другой? А если так:
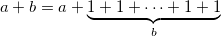
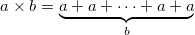
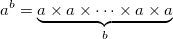
Обобщенно эти операции называются гипероператорами. Для сложения, умножения и возведения в степень — 1-го, 2-го и 3-го порядка соответственно. Продолжение этого ряда на более высокие порядки напрашивается само собой: гипероператором 4 порядка (тетрацией) называют последовательное возведение в степень:
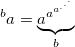
А вот для гипероператоров более высоких порядков использовать такую систему обозначений уже не получится — уж больно громоздкими и запутанными будут степенные башни. Поэтому для обозначение больших чисел используются другие системы нотаций.
Одной из наиболее распространенных является стрелочная нотация Дональда Кнута, предложенная в 1976 году. Принцип записи чисел вытекает из последовательности гипероператоров и по большому счету представляет собой явное указание порядка гипероператора. Обычное возведение в степень (гипероператор 3 порядка) обозначается одной стрелкой: a↑b, тетрация — двумя стрелками a↑↑b и так далее. Вот как вычисляется тетрация:
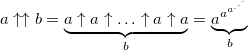
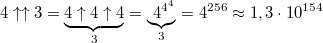
Изменив всего одну цифру мы получаем гигантский рост значения числа:
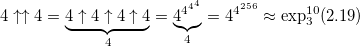— в этом числе более, чем 10153 цифр.
Добавив еще одну стрелку мы получаем гипероператор 4 порядка — пентацию:
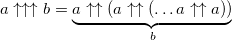
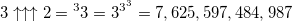
Изменение одной цифры здесь приводит к столь большому росту значения, что эпитеты можно и не подбирать:
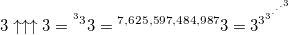— высота степенной башни составляет 7,625,597,484,987 элементов…
(это число назвается тритри, и оно нам еще пригодится)
Чтобы не рисовать много стрелок, используется сокращенная запись: a↑nb для обозначения a↑↑...↑b с n стрелок.
Тут нужно быть крайне аккуратным в оценках скорости роста функции по мере увеличения порядка гипероператора (вы явно ошибётесь в меньшую сторону) — если три не пентировать, а гексировать в три (ну просто увеличить n на единицу), то мы должны 3 два раза пентировать по три, то есть 3 пентировать в три 7,625,597,484,987 раз… (но не расслабляйтесь, всё это только начало, самое начало).
Кстати, вы уже догадались, каково самое слабое место стрелочной нотации Кнута? Да, именно n — количество стрелок. А что, если оно столь велико, что обычное число уже не в состоянии его передать? Короткое отступление: если три, пентированное в два, поддается хоть какому-то пониманию, то уже три, пентированное в три, ни представить, ни осознать невозможно. Даже не заикаясь о следующих порядках гипероператоров. Это область чистой незамутненной абстрактной математики и, чёрт возьми, it's fucking awesome!
Решением проблемы нотации Кнута являются цепочки Конвея. Они используются тогда, когда для записи числа даже стрелочная нотация Кнута становится слишком громоздкой. Помните про число Грэма, которое упоминалось в самом начале? Обозначить его стрелками Кнута просто невозможно. Определение цепочки и её взаимосвязь со стрелочками Кнута:
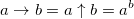
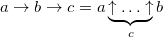
Вроде бы всё одно и то же. Но проблема «количества стрелочек» в цепочках Конвея решается легко и изящно: добавлением еще одной стрелки. А каждая стрелка обращает всю предыдущую цепочку на себя. Попробуем разобраться на примере: возьмем тетрацию 3 → 3 → 2 (что это такое: берем первые два числа и проделываем операцию возведения в степень три раза), добавим справа → 2.
3 → 3 → 2 → 2 = 3 → 3 → ( 3 → 3 → 1 → 2) → 1 = 3 → 3 → (3 → 3) = 3 → 3 → 27
Добавив всего однy стрелочку мы сразу перешли к гипероператору 27 порядка. И число Грэма, никак не представляемое в стрелочной нотации Кнута, цепочками Конвея записывается очень лаконично: 3 → 3 → 64 → 2. А ведь можно продолжать добавлять стрелочки и переходить ко всё более невообразимым порядкам чисел.
Ха! Но разве это правильно, рисовать столько стрелок? Да и слишком уж ме-е-едленно растут числа… В общем, Джонатан Бауэрс ввел массивную нотацию (array notation), которая в своей максимально расширенной форме называется BEAF (Bowers Exploding Array Function, взрывная массивная функция Бауэрса, игра слов с английским beaf — говядина. Надо отметить, что Бауэрс даже в своих научных трудах отличается особым чувством юмора). Запись ее очень проста и напоминает уже рассмотренные нотации: 3↑↑↑3 = 3 → 3 → 3 = {3,3,3}. Используется также другая система массивной нотации, когда последний элемент, обозначающий порядок гипероператора, переносится в середину записи, т.е. {3,3,2} = 3 {2} 3 (логика такая — берем две цифры по краям и делаем с ними то, что указано в середине).
На данном этапе никаких отличий массивной нотации от цепочек Конвея нет. Но добавление четвертого элемента массива имеет принципиально другой смысл, а именно — количество скобочек: {3,3,3} = {3,3,3,1}, {3,3,3,2} = {{3,3,3}}.
{a,b,1,2} = a {{1}} b = a { a { a....a { a { a } a } a… a } a } a, где b — количество a, расходящихся от центра.
Для наглядности посмотрим, что происходит при изменении элемента внутри центральных скобочек «всего на единицу»:
{3,3,1,2} = 3 {{1}} 3 = 3 {3 {3} 3} 3 = {3, 3, {3, 3, 3}} = {3, 3, тритри}
{3,3,2,2} = 3 {{2}} 3 = 3 {{1}} 3 {{1}} 3 = {3, {3, 3, тритри}, 1, 2} = 3 {3 {3… 3 {3 {3} 3} 3… 3} 3} 3, где количесто троек, расходящихся от центра к краям, равно {3,3, тритри}.
В сравнение с цепочками Конвея взрывной рост числа происходит на этап раньше — если у Конвея лишь четвертое число обращает все предыдущие операции на себя, то у Бауэрса — уже третье. Яркий пример с рассмотренными выше числами:
у Конвея третья единица «съедает» остаток цепочки 3 → 3 → 1 → 2 = 3 → 3 = 27, то у Бауэрса она как раз «работает» на дальнейший его рост: {3,3,1,2} = {3,3, тритри}.
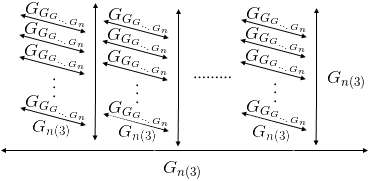
Кстати, это был всего лишь массив из 4 элементов. Добавим безумия? Просто увеличивать количество элементов массива через запятую, следуя уже сформулированным правилам работы с ними — это неинтересно. Поэтому Бауэрс придумывает видоизмененные «скобки» для того, чтобы хоть минимально наглядно «представить» числа в массивной нотации. Четвертое число в массиве еще остается с фигурными скобками, а дальше начинается форменное безобразие: пятое — квадратные скобки, повернутые на 90 градусов, шестое — кольца вокруг предыдущей конструкции, седьмое — обратные угловые скобки, восьмое — как трехмерные квадратные… Короче, проще это показать:
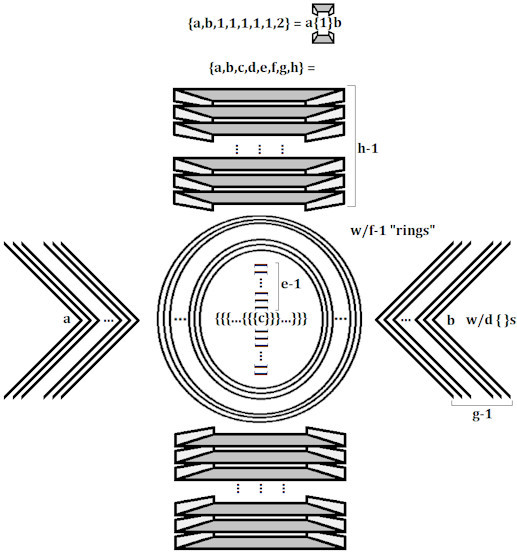
(еще на подобные картинки можно посмотреть здесь)
Вы думаете, что Бауэрс на этом остановился? Как бы не так. Ну вот что, ЧТО еще можно придумать в записи массивов? А можно обратить внимание, что там есть запятые… Которые пусть обозначают элементы одномерного массива. А если поставить между числами (1), то это переход на следующую строку, (2) — переход на следующую плоскость.
Квадрат из троек («дутритри») записывается как {3,3,3(1)3,3,3(1)3,3,3}.
Куб из троек («диментри») — {3,3,3(1)3,3,3(1)3,3,3(2)3,3,3(1)3,3,3(1)3,3,3(2)3,3,3(1)3,3,3(1)3,3,3}.
Вот так незатейливо мы перешли от плоскостных массивов к объемным (и заметьте, это всего лишь запись некого числа, которая из-за своих масштабов потребовала выйти из плоскости просто в своем написании!). Разумеется, дальше мы вводим новые обозначения для четырехмерных, пятимерных «объектов» (простите, называть эти монструозные контрукции числами уже сложно). Например, & означает «массив из»: {10,100,2} & 10. То есть {10,100,2}-массив десяток, или же 10↑↑100-массив десяток. Ну то есть нужно 100 раз возвести десять в десятую степень, построить решетку с таким количеством ячеек (причем она будет находиться в стозмерении, то есть измерении измерений измерений… измерений (слово повторено сто раз)), затем заполнить все ячейки десятками — и только тогда можно приниматься решать этот массив.
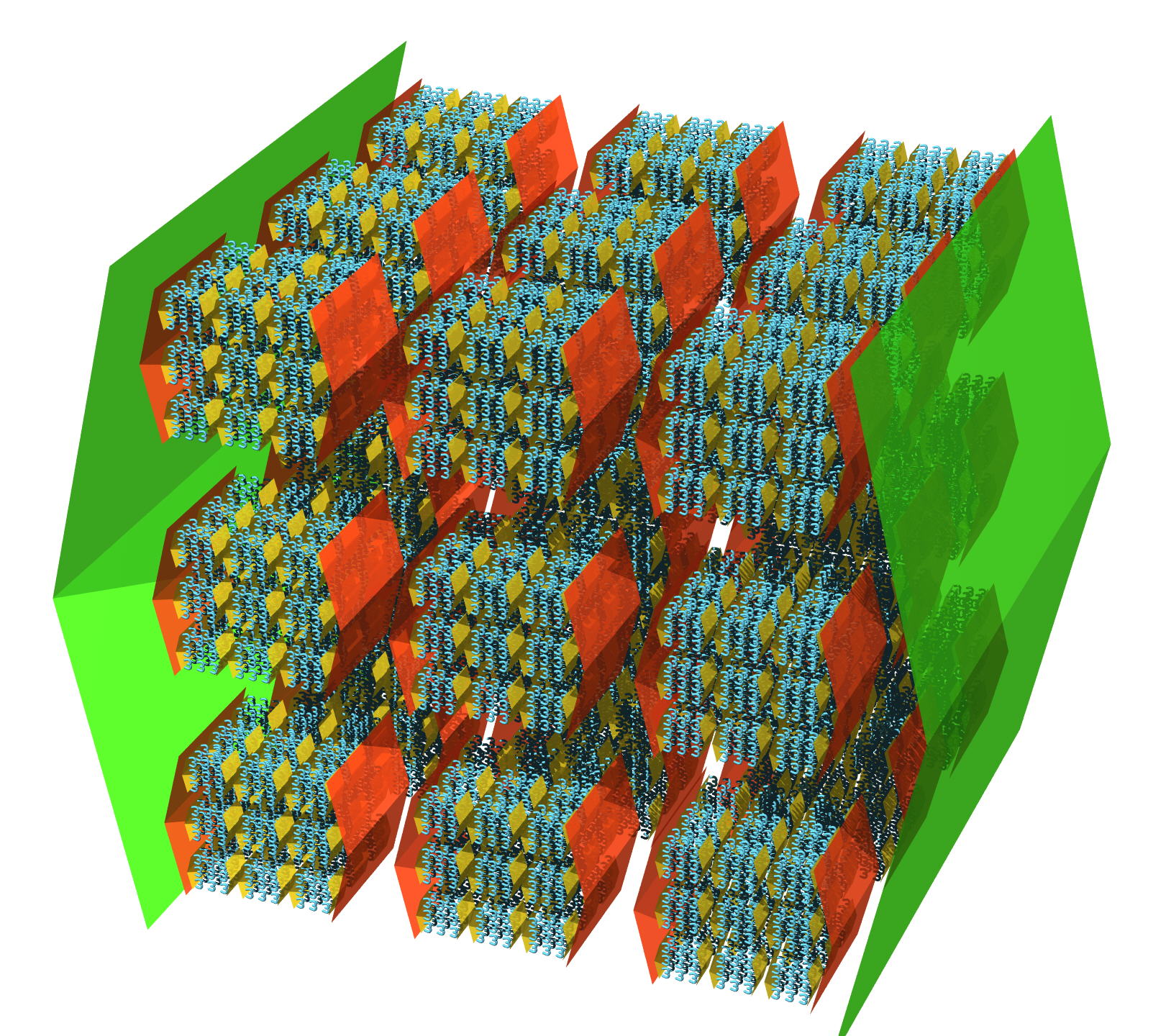
Думаете хотя бы на этом всё? Неа. Обозначим «легион» прямым слэшем (/). В массиве {a,b,c,.../2} двойка находится во втором легионе. Сначала мы должны решить первый легион (слева от косой черты), а затем взять такое количество элементов в цепочке «массив из… массив из… массив из...», которое получилось при решении: {3,3 / 2} = 3 & 3 & 3 = {3,3,3} & 3. А вот если взять {3,3,3 / 3} = {3 & 3 & 3 / 2}. На этот раз тритри — это не количество элементов в массиве, а количество элементов в цепочке 3 & 3 &… & 3 & 3.
Еще одно расширение Бауэрс сделал добавив символ @ (a@b обозначает «легионный массив размера a из b») и обратный слэш (лугион). Ну тут уже всё понятно: {a,b 2} = a @ a @ a… a @ a @ a (где а повторяется b раз).
Понятно, что процесс придумывания новых наименований для каких-то операций не может быть бесконечным (за легионами и лугионами идут лагионы, лэгионы и лигионы, но очевидно, что это ничто, учитывая наш размах), поэтому Бауэрс сделал проще — определил L как прогрессию из легионов, лугионов, лагионов, лэгионов и лигионов: L1, L2, L3… И далее число опередляется индексами.
Например для «вычисления» (смешно, конечно, говорить о вычислениях на таких масштабах) {L100,10}10,10 нужно взять сотый член в прогрессии «легионы, лугионы, лагионы...» и составить из него массив в 10 измерениях. Затем нужно убирать по одному члену, каждый раз добавляя цепочку из «10 % 10 %… %10» (где % — L100-гионный массив из на то количество десяток, которое получилось на предыдущем этапе. И только после того, как все сотые члены (а также L99, L98 и иже с ними, вплоть до и /) закончатся, мы сможем, собственно, начать решать первый массив в сумасшедшей прогрессии массивов.
Кстати, для 340 больших чисел Бауэрс ввел собственные наименования, многие из которых по своей безумности полностью соответствуют алгоритмам расчета. Встречайте, МЕАМЕАМЕАЛОККАПУВА УМПА: {{L100,10}10,10 & L,10}10,10.
Примечание для нердов:
Разумеется, Бауэрс определил строгий набор правил совершения операций над массивами.
Определения:
— первый запись в массиве называется «базой» (base) — b;
— вторая запись в массиве называется «начальной» (prime) — p;
— первая неединичная запись после начальной называется «пилотом» («pilot»);
— запись массива, которая следует сразу за пилотом называется «вторым пилотом». Она не существует, если пилот является первой записью в своем ряду;
— структура — это часть массива, которая состоит из групп меньшей размерности. Это может быть запись (Х0), ряд (Х1), плоскость (Х2), область (Х3) и т.д., не говоря уже о структурах большей размерности (Х5, Х6 и т.д.) и тетрационных структурах, например, X↑↑3. Можно также продолжить пентационными, гексационными и т.п. структурами.
— «предыдущей записью» (previous entry) называется запись, которая образуется перед пилотом, но в том же ряду, что и остальные предыдущие записи. «Предыдущим рядом» называется ряд, который появляется перед пилотным рядом, но в той же плоскости, что и все остальные предыдущие ряды и т.д.
— «начальный блок» (prime block) структуры S вычисляется заменой всех вхождений Х на p. Например, если S = Х3, то начальным блоком будет p3 или куб со стороной длины p. Начальным блоком Хх-структуры будет pp, p-гиперкуб с длиной стороны p.
— «самолёт» включает в себя пилота, все предыдущие записи, а также начальный блок всех предыдущих структур;
— «пассажиры» — это записи в самолете, которые не являются пилотом или вторым пилотом;
— значение массива записывается как v(A), где А — это массив.
Правила вычисления:
1. Если p = 1, v(A) = b
2. Если нет пилота, то v(A) = bp
3. Если первое и второе не применяется, то:
— пилот уменьшается на 1;
— второй пилот принимает значение оригинального массива с начальным значением, уменьшенным на 1;
— каждый пассажир становится b;
— остальная часть массива не изменяется
Все примеры, описанные выше, подчиняются этим незатейливым правилам.
Как уже говорилось выше, BEAF по своей мощи значительно превосходит цепочки Конвея, не говоря уже о нотации Кнута… Интересно, что дальше?
А дальше мы вступаем на поле скорее философии, нежели собственно математики. Все описанные выше нотации представляют собой вычислимые функции или функции, которые могут быть реализованы на машине Тьюринга.
Во второй части мы рассмотрим невычислимые функции: задачу усердных бобров, сигма-функцию Радо Σ(n), число Райо, BIG FOOT и другие, а также рассмотрим быстрорастущую иерархию, чтобы понять, есть ли предел этому математическому безумию.
Использованные материалы:
1. Главный сайт по гугологии: http://googology.wikia.com/wiki/Googology_Wiki
2. Бесконечноскрёбы Джонатана Бауэрса
3. Exploding Array Function
Автор: Kamalesh
