По следам «четырёх стаканов» или нужно ли знание точных математических формул физических процессов, или достаточно базовых знаний и логики рассуждений.
«Образование – это то, что остается, когда все выученное забыто»
Макс фон Лауэ, Беррес Фредерик Скиннер, Джордж Галифакс и, возможно, кто-то ещё.
Не только вся разумная человеческая жизнь (ключевое слово – разумная), но и жизнь вообще стремится к оптимизации процессов жизнедеятельности. Заметьте, не к минимизации, а к оптимизации, т.е. к повышению т.н. условного КПД процесса. Т.е. достижению результата с минимальными усилиями.
Начав читать статью «Задача про четыре стакана», ожидал общих рассуждений и появления формул в общем виде чисто для иллюстрации и наглядности. Однако, автор решил быть пунктуально строг. Да, он рассмотрел задачу и решил её довольно красиво. Однако, возник вопрос, можно ли её решить верно, не прибегая к конкретным формулам описания физического процесса? Решить, так сказать, на пальцах? Давайте попробуем. Итак (повторю исходные, вводные данные) имеем две пары одинаковых стаканов, в каждой из которых один стакан наполнен «холодной» водой, другой – «горячей».
Суть эксперимента: смешиваем воду из первой пары и ждём 10 минут. Смешиваем воду из второй пары стаканов. Замеряем температуру обоих смесей воды. В какой смеси температура будет выше/ниже или она будет одинакова?
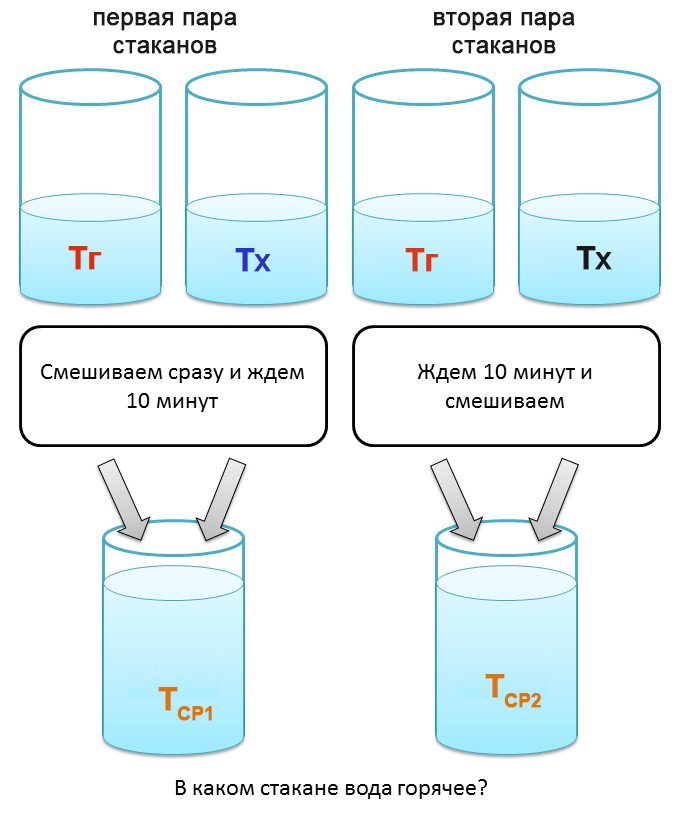
Что главное в такого рода задачах-загадках? Главное – фраза «при всех прочих равных условиях».
Значит, первым делом необходимо выделить условия неравные. Что это за условия? Это температура тел и их объём-поверхность. Что можно сказать о физике и математике процесса? Скорость остывания/нагревания тела зависит от:
1) Разности температур нагретого/охлажденного тела и окружающей среды (это физика);
2) Соотношения объёма и поверхности тел (это физика);
3) И имеет вид экспоненциальной (логарифмической) функции (это математика).
Что такое «изменение по экспоненте/логарифму»? Это изменение в n-раз. Что это значит? Это значит, что измеряемый параметр независимо от его начальной и «конечной» величины изменится не «на», а «в» конкретное количество раз в зависимости от времени (или другого параметра/аргумента функции).
Т.е. если одно тело имеет начальную температуру 100 градусов, а другое 40 градусов, то при прочих равных условиях при охлаждении первого тела в два раза оно будет иметь температуру 50 градусов, а второе будет иметь температуру в 20 градусов. Даже неважно каких градусов – в Кельвинах или в Цельсиях измерять – ведь прочие условия равны.
Такую же зависимость демонстрирует уровень звукового давления в зависимости от начального значения (роль температуры в нашей задаче) и расстояния (роль времени в нашей задаче).
Думаю, читатели смогут сами дополнить список «экспоненциальных» физических процессов. Т.е. с физической сущностью «экспоненциального» процесса мы наглядно разобрались. Оставив пока п.2. вне рассмотрения, посмотрим через картинки варианты прохождения процесса остывания/нагревания.

Рис. 1 Обозначения
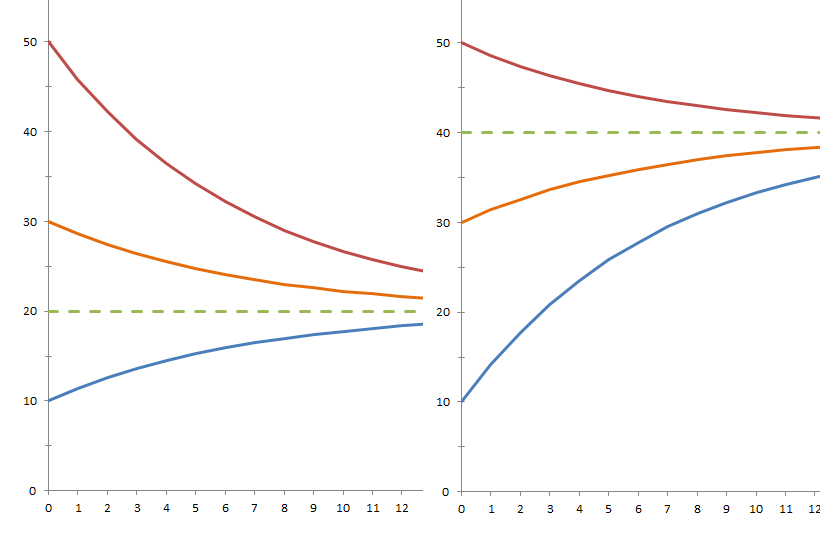
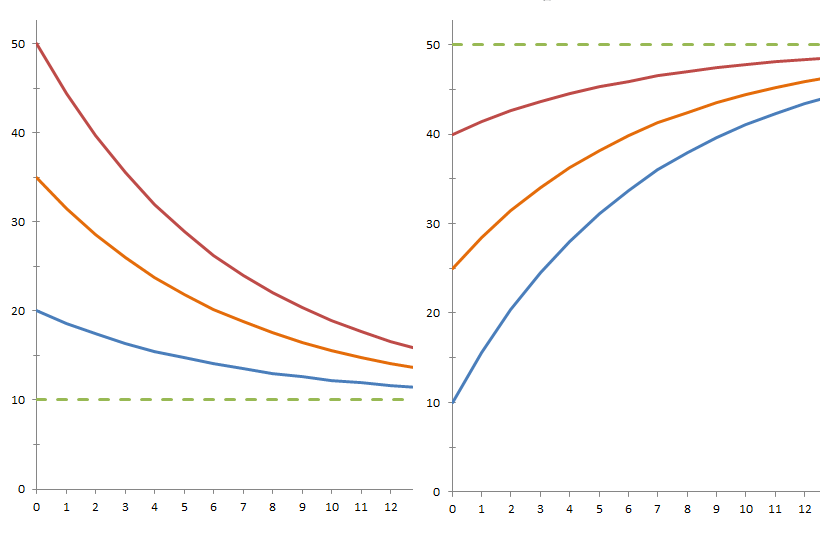
Рис. 2, 3. Варианты «несимметричных» исходных температур.
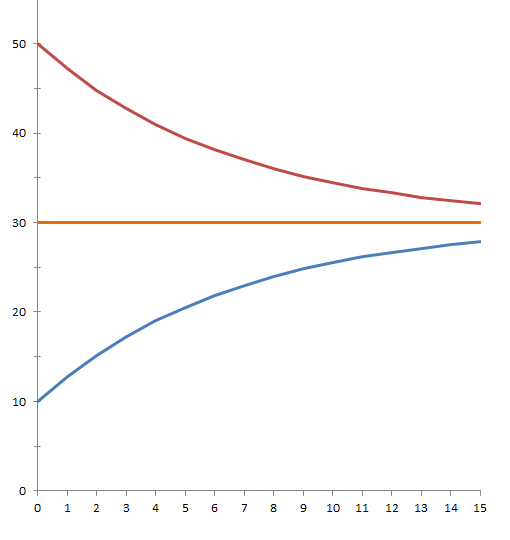
Рис. 4. Вариант «симметричных» исходных температур относительно температуры окружающей среды.
Итак, мы видим (не на картинках, а логически), что без учёта п.2. температура тела содержимого первой пары стаканов будет равна температуре тела содержимого второй пары не только через условные 10 минут, но и через любой момент времени.
Обратимся к п.2. Будем говорить про объём и поверхность, а не массу, т.к. различия именно в объёме и поверхности. Все остальные условия равны, как мы помним. Количество тепла, которое тело отдаёт/принимает, пропорционально объёму. Сопротивление передачи пропорционально поверхности.
Значит, чем больше соотношение поверхности к объёму, тем быстрее идёт процесс передачи тепла. Чем меньше тело, тем быстрее оно нагревается/остывает (помните, что малыш на морозе быстрее замерзает, чем взрослый? Именно по этой причине). Стало быть, отдельно стоящие стаканы – вторая пара – приведёт свою температуру к температуре окружающей среды быстрее. С математической (да и физической) точки зрения это равносильно увеличению времени.
Если температуры «холодной» и «горячей» воды равно отстоят от температуры окружающей среды, то конечные температуры смесей будут равны. Это, так сказать, «симметричный» вариант. Если же одна из исходных температур будет «отстоять дальше» от температуры окружающей среды, то из-за более интенсивного обмена теплом в «отдельном» стакане (вторая пара) она быстрее приблизится к температуре окружающей среды и уже не внесёт своего «полного вклада» в сохранение первоначального состояния. Т.е. если «холодная» вода «холоднее», чем «горячая» «горячее», то вторая пара (из-за более быстрого процесса теплообмена) будет теплее первой пары стаканов. И наоборот.
Итак, не прибегая ни к одной математической формуле нам удалось найти ответ, поставленный в задаче о четырёх стаканах. Нужны ли формулы? Безусловно, если вам необходимо вычислить конкретные величины.
Автор: pencilTM






