
Недавно набрел в «Википедии» на статью о так называемой самой сложной логической задаче. Статья потрясла меня то ли своей провокационностью, то ли логической безграмотностью, особенно в части авторских пояснений её условий и возможного хода решения.
Условие задачи
Есть три бога: A, B и C, один из которых бог истины, другой – лжи, а третий — случая. Бог истины всегда говорит правду, бог лжи — всегда обманывает, бог случая может говорить и правду, и ложь. Требуется определить богов, задав 3 вопроса, на которые можно ответить «да» или «нет». Каждый вопрос задаётся только одному богу. Боги понимают язык, но отвечают на своём языке, в котором есть 2 слова «da» и «ja», причём неизвестно, какое слово обозначает «да», а какое «нет».
Сначала разберем решение этой задачи циничным способом. Кратко способ характеризуется двумя тезисами:
- Задача должна быть сведена к системе логических уравнений и неравенств (СЛУН);
- Ограничения на значения входных переменных записываются в реляционные таблицы. Решение СЛУН осуществляется выполнением SQL-запроса. Построенная реляционная таблица содержит 0 или более решений логической задачи. Каждая строка таблицы – это одно из решений логической задачи.
Проиллюстрируем наши тезисы решением самой сложной логической задачи.
Обозначим А.СТАТУС, В.СТАТУС и С.СТАТУС переменные СЛУН, которую мы сейчас составим. Возможные значения переменных – строковые значения «ИСТИНА», «ЛОЖЬ» И «СЛУЧАЙ». Для их обозначения ниже будем использовать идентификаторы ИСТИНА, ЛОЖЬ И СЛУЧАЙ.
Изучение условия задачи позволяет составить одно логическое уравнение:
(A.СТАТУС<>B.СТАТУС AND A.СТАТУС<>С.СТАТУС AND B.СТАТУС<>C.СТАТУС AND) EQV TRUE — это формальная запись первого условия задачи.
SQL-запрос для решения уравнения имеет вид:
SELECT * FROM А, В, С WHERE (А.СТАТУС, В<>СТАТУС AND А.СТАТУС <> С.СТАТУС AND В.СТАТУС <> С.СТАТУС) EQV TRUE;Решения уравнения (их 6) и одна из таблиц с ограничениями на значения входных переменных представлена на рисунке ниже:
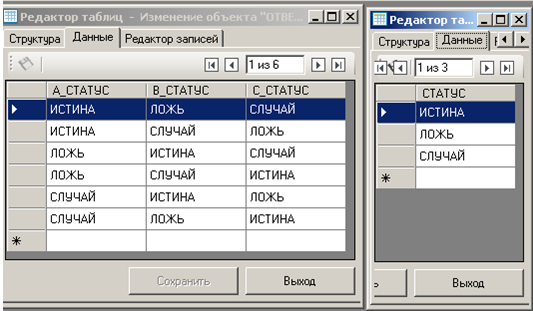
Любое из шести решений уравнения и есть ответ на вопрос задачи. Этот ответ получен без бесед с богами.
Чтобы поддержать «дедуктивный» диалог с целью получения единственного варианта ответа, зададим каждому из богов по одному вопросу, например:
Богу А: «Не является ли бог С богом случая?». Богу В: «Не является ли бог А богом лжи?». Богу С: «Не является ли он богом случая?» Формально эти вопросы могут быть записаны в виде системы из 6 логических неравенств, решением которой будет единственный ответ: А – бог истины, В – бог лжи, а С – бог случая. Отметим, что ответы богов — «da» или «ja» для решения задачи не нужны.
Система неравенств имеет вид:

Дополним конъюнктивно предложение WHERE нашего SQL-запроса этой формулой и получим ответ на вопрос задачи в виде реляционной таблицы с одной строкой.
Адресуя наши вопросы богам в другом порядке, например, первый вопрос богу В, а второй – богу А, можно получить любой другой ответ из числа возможных решений логического уравнения, приведенных на первом рисунке.
Применение тезиса о формализации логической задачи системой (или несколькими системами) логических уравнений и неравенств позволяет четко фиксировать условия задачи. В постановке самой сложной логической задачи дано только одно уравнение. Для получения единственного ответа автор задачи неявно предлагает дополнить ее условие, что мы и сделали, сформулировав 6 троек вопросов. Тезис о формализации логических задач СЛУН заставляет это понимать без экивоков.
Превращение СЛУН в SQL-запрос нетрудно автоматизировать. Для некоторых разновидностей СЛУН и диалектов SQL это уже сделано (ознакомиться с решением других задач, дополнительной информацией и материалами можно здесь). Особый интерес представляют системы логических уравнений, решение которых осуществляется выполнением рекурсивных SQL-запросов.
Автор:





