Привет! Представляю вашему вниманию перевод статьи "Math Origins: The Logical Ideas" автора Erik R. Tou (University of Washington Tacoma).
От переводчика:
В журнале Математической ассоциации Америки был опубликована серия статей об истоках математики вообще и нотации в частности. Последние две из опубликованных к текущему моменту пяти статей показались мне наиболее интересными, поэтому я публикую перевод первой из них — «Math Origins: The Logical Ideas».
Как только студент-математик набивает руку в математическом анализе и статистике, наступает момент, когда становится явной логическая суперструктура математики. Это может проявиться в виде явных вопросов, или хотя бы определенного дискомфорта касательно предполагаемой достоверности математических истин. Как мы можем быть уверены в правдивости классических результатов — таких как теорема Лагранжа или центральная предельная теорема? Это та самая точка, в которой многие программы бакалавриата по математике начинают включать курс по математической логике и мысли.
По собственному опыту автора [Эрика Тоу — прим. пер.], это обычно включает в себя изменение порядка идей, от «порядка открытий», столь распространенного в решении проблем, до «порядка логики», который формирует фундамент для математических доказательств. Очень быстро становится очевидно, что новая терминология и нотация необходимы для того, чтобы пролить свет на рассматриваемые математические утверждения и логические отношения. Такие понятия, как конъюнкция и дизъюнкция, импликация и эквивалентность, универсальность и экзистенциальность должны тщательно разделяться. На сегодняшний день теория логики и присущая ей нотация рассматриваются нераздельно: одно не существует независимо от другого. Однако, это не всегда было так! В этой статье мы рассмотрим некоторые ранние попытки организовать теорию логики систематическим путём, вместе с несколькими принятыми решениями касательно нотации. Мы увидим, что авторы 17-го и 18-го столетий были, приемущественно, заинтересованы в описании способа размышления о логике, обычно через аналогию с уже существующими математическими или философскими концепциями. В следующей статье из этой серии мы продолжим повествование в 19-ый и 20-ый века, чтобы изучить множество систем нотации, предложенных для описания логики.
Ранние символы Иоганна Рана
Для многих учащихся часть логических символов появляются в начале изучения математики, зачастую как сокращения или аббревиатуры для упрощения мыслительного процесса. Хорошим примером может служить использование символа «$inline$therefore$inline$» для «следовательно», использующегося для завершения цепочки рассуждений. Среди первых, кто начал использовать этот символ, был шведский математик Иоганн Ран. В книге 1659-го года «Teutsche Algebra» («Немецкая алгебра») Ран попытался донести алгебраический вклад Виета, Декарта и других до немецкоговорящей аудитории. В процессе он использовал множество условных обозначений для выражения этих идей. Вот выдержка:

Рис. 1. Алгебраическое доказательство в «Teutsche Algebra» Иоганна Рана использует $inline$therefore$inline$ для «следовательно» и $<!-- math>$inline$$inline$</math -->$ для умножения. Оцировано Google Books из копии, принадлежащей Баварской Национальной Библиотеке.*
Во второй строке этого пассажа Ран применяет символ «$inline$therefore$inline$» в том же значении, что и латинское ergo. Этот символ используется как заключение аргументации, которая следует непосредственно за ним: пропорция $inline$18sqrt{dd-cc} : (c+d)sqrt{dd-cc} :: 18 : c+d$inline$ из шага 2 сводится в шаге 3 к тавтологическому равенству $inline$(18c + 18d)sqrt{dd - cc} = (18c + 18d)sqrt{dd - cc}$inline$. Сегодня мы бы описали этот шаг как использование перекрестного умножения и дистрибутивности для решения задачи на дроби. Согласно Кэджори [Caj, стр. 212], это было первое использование «$inline$therefore$inline$» в значении «следовательно». Мы должны также отметить колонку в правой части страницы, в которой он ссылался на предыдущие шаги вместе с сокращенным описанием логики для данного шага.
Обозначения Рана на этом не закончились; через 20 страниц он использовал несколько новых символов, чтобы разъяснить логику знакомых алгебраических доказательств.

Рис. 2. Некоторые интересные логические символы из «Teutsche Algebra» Иоганна Рана. Оцифровано Google Books из копии, принадлежащей Баварской Национальной Библиотеке.
В этой выдержке Ран представил подход к решению старой задачи: по заданным числам $inline$D$inline$ и $inline$F$inline$ найти такие числа $inline$a$inline$ и $inline$b$inline$, сумма и произведение которых равны $inline$D$inline$ и $inline$F$inline$, соответственно. Ран ввёл спиральный символ для возведения в степень в строке 3, звёздочку $inline$*$inline$ для умножения в строке 4 и нечто, что может быть описано только как «загогулина», для квадратного корня в строке 6. В конце он нашел выражение для $inline$a-b$inline$, которое в дальнейшем может быть прибавлено к $inline$a+b=D$inline$ или вычтено из него, таким образом повторяя формулу корней квадратного уравнения. В данном случае эти символы — условные обозначения для организации логики аргументации, не слишком уж отличные от двухколоночных доказательств, которые используются современными учащимися для организации математических выкладок.
Стремление Лейбница к универсальной математике
В каком-то смысле, Ран просто ввел некоторые символы, чтобы упростить существующие доказательства, вместо того, чтобы систематически думать о том, как доказательства были построены. (Надо отдать Рану должное — это было ценным новшеством в эпоху, когда затраты на бумагу и печать были нетривиальным фактором). Действительно, не прошло и поколения, как была предпринята попытка систематизировать логику никем иным, как Готфридом Вильгельмом Лейбницем. Для философски настроенного ученого, такого как Лейбниц, это было частью более амбициозного проекта: символического и строгого универсального исчисления, которое можно применить к любому проекту в области человеческих исследований. Это была исследовательская программа, которую Лейбниц проводил в различных формах на протяжении всей своей долгой карьеры. Как описывал Гарретт Томсон в книге «О Лейбнице», Лейбниц преследовал три основные цели:
- Создать алфавит логики, которым можно кодировать понятия в числовой форме;
- Создать словарь логики, чтобы переводить сложные понятия на язык чисел;
- Создать синтаксис логики, чтобы управлять способами осуществлять логические выводы.
Первая цель наметилась в работах Лейбница еще в 1666 году, в трактате «Dissertatio de Arte Combinatoria» («Диссертация на тему искусства комбинаций») [Lei]. В частности, Лейбниц утверждал, что все высказывания (1) могут быть изложены в форме субъекта-предиката, а также (2) могут быть построены как «комплексы» (или комбинации) простых высказываний. Подсчитав количество способов сделать эти комплексы из набора простых высказываний, Лейбниц пришел к треугольнику Паскаля из комбинаторики.
Интересно, что этот ранний трактат по логике был единственной такой работой, опубликованной Лейбницем при его жизни. Однако Лейбниц посвятил много времени своему глобальному проекту, в конечном итоге написав более десятка трактатов по различным логическим темам. 1679 год был, по-видимому, плодотворным временем для Лейбница, поскольку он написал шесть работ по универсальному исчислению той весной. Мы рассмотрим одну из этих шести работ, амбициозно названную «Regulæ ex quibus de bonitate consquentiarum formisque et modis syllogismorum categoryoricorum judicari potest per per numberros» («Правила, на основании которых можно принимать решение с помощью чисел, относительно действительности умозаключения и о формах и настроениях категориальных силлогизмов»). В своем первом примере Лейбниц деконструировал утверждение «Каждый мудрец благочестив» следующим образом:
Истинное универсальное утвердительное предложение, например,
Каждый мудрец благочестив
$inline$+20−33+10−3$inline$
$inline$+cdh-ef+cd-e$inline$
— это такое, в котором любое символическое число субъекта (например, $inline$+20$inline$ и $inline$-33$inline$) может быть точно разделено (т.е. таким образом, чтобы не осталось остатка) на символическое число того же знака, принадлежащего предикату ($inline$+20$inline$ на $inline$+10$inline$, $inline$−33$inline$ на $inline$−3$inline$). Таким образом, если вы поделите $inline$+20$inline$ на $inline$+10$inline$, вы получите $inline$2$inline$ без остатка, а если вы поделите $inline$-33$inline$ на $inline$−3$inline$, вы получите $inline$11$inline$ без остатка. И наоборот, когда это не так, утверждение неверно. [Par, стр. 26]
Здесь следует сделать три важных замечания. Во-первых, Лейбниц был осторожен, чтобы различать субъект и предикат в своих высказываниях. Действительно, в начале статьи он заметил, что «у каждого категориального предложения есть субъект, предикат, связка; качество и количество». В приведенном выше примере субъект «мудрец» и предикат «благочестивый» связаны через связку «есть», а качество предложения «положительно». По словам Томсона [Tho, стр. 20], отношение субъект-предикат было одним из фундаментальных предположений Лейбница о логике. Во-вторых, Лейбниц также различал универсальные и частные высказывания. Сегодня мы ссылаемся на связанные квантором всеобщности и связанные квантором существования утверждения. Это повышает уровень точности, возможный при формулировании предложений. Наконец, оба предыдущих факта позволили закодировать суждение с точки зрения целочисленной делимости. В частности, предикат будет «делиться нацело» на субъект именно тогда, когда утверждение верно.
Более общий взгляд: «Algebræ Philosophicæ» Ричери
Перенесемся в 1761 год, когда появилась в печати «Algebræ philosophicæ in usum artis inveniendi» («Алгебра философии, для использования в искусстве открытия») Людовико Ричери. Как намекает название, Ричери ввел набор обозначений для лучшего выражения логических идей.



Рис 3. Набор символов Ричери для представления логических идей в «Algebræ Philosphicæ» (1761). Оцифровано Archive.org по копии, принадлежащей библиотеке Музея естественной истории, Лондон.
Как видно, две полукруглые дуги используются в различных комбинациях для представления логических идей. Например, символ, напоминающий греческую литеру $inline$omega$inline$, использовался для высказываний, которые признавались истинными, в то время как инвертированная версия символа использовалась для противоречивых высказываний. Далее в тексте встречается список пар символов для выражения противоположных идей в логике: сущее и несуществующее, положительные и отрицательные определения, определенное и неопределенное, возможность и невозможность, изменяемое и неизменное. Важнее всего, символы Ричери для сущего (aliquid) и несуществующего (nihil) напоминают современные символы для объединения ($inline$cup$inline$) и пересечения ($inline$cap$inline$), соответственно. Кульминацией этой короткой статьи является логическая диаграмма, которая отслеживает возможные результаты любого объекта критического исследования.
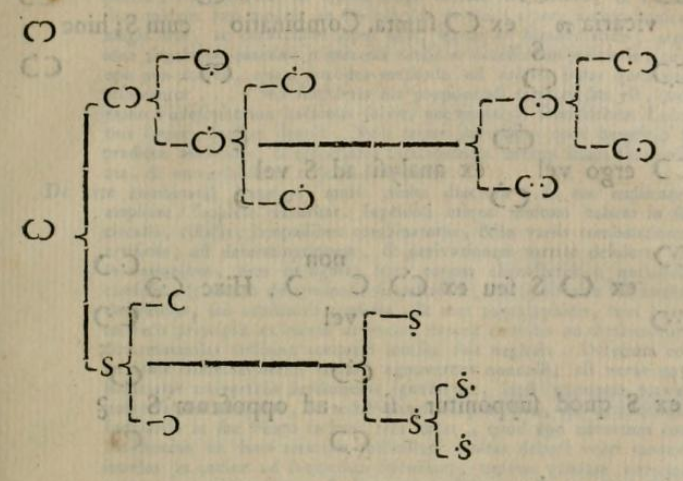
Рис. 4. Дерево символов логики Ричери из «Algebræ Philosphicæ» (1761). Оцифровано Archive.org по копии, принадлежащей библиотеке Музея естественной истории, London.
В чисто символической форме Ричери предоставил своего рода бинарный поиск для философского исследования — действительно, это та самая алгебраическая философия, которая была обещана! В общем, дерево начинается так:
- Любое утверждение либо невозможно (противоречиво, перевернутая $inline$omega$inline$ в углу), либо возможно (непротиворечиво, $inline$omega$inline$ в левом конце дерева);
- Если утверждение возможно ($inline$omega$inline$), оно может быть либо детерминированным (доказано, нижняя ветвь), либо неопределенным (недоказанное, верхняя ветвь);
Следуя чуть дальше по дереву, мы видим, что любое возможное, детерминированное утверждение должно быть либо положительным, либо отрицательным. Также интересно, что Ричери рассматривал возможные неопределенные утверждения как либо определяемые (доказуемые), либо неопределимые (недоказуемые). В общей сложности «Algebræ Philosphicæ» Ричери занимает всего 16 страниц, причем многие из них состоят из символических представлений для различных высказываний. Если вам почудилось эхо Лейбница в этой статье, вы правы! Это не случайно: в своей работе Ричери специально упомянул «Dissertatio de Arte Combinatoria». В частности, мы можем видеть, как субъектно-предикатная форма предложения была перенесена в «Algebræ Philosphicæ».
Zeichenkunst in der Vernunftlehre Ламберта
Незадолго после того, как была опубликована алгебра философии Ричери, Иоганн Ламберт сделал собственную попытку символизации рассуждений в работе 1782 года «Sechs Versuche einer Zeichenkunst in der Vernunftlehre» («Шесть попыток символического метода в теории разума»). Вот символы Ламберта со страницы 5:

Рис. 5. Иоганн Ламберт заимствовал символы из алгебры и арифметики для представления логических идей в «Sechs Versuche einer Zeichenkunst in der Vernunftlehre» (1782). Оцифровано Google Books по копии, принадлежащей Баварской государственной библиотеке.
Мы видим, что символы Ламберта являются более математическими и менее философскими, чем символы Ричери. В дополнение к заимствованию символов из математики, их значения легко узнаваемы для любого изучающего логику; например, обратите внимание на знаки равенства ($inline$=$inline$), сложения ($inline$+$inline$), разделения ($inline$-$inline$), оппозиции ($inline$times$inline$), универсальности ($inline$>$inline$) и особенности ($inline$<$inline$). Идея здесь заключается в том, что весь анализ логических идей должен и может быть сведен к форме арифметики. В этом смысле подход Ламберта гораздо ближе к Лейбницу, поскольку он опирается на аналогию между логикой и арифметикой. (Также обратите внимание, что все трое различают универсальное и частное).
Чтобы увидеть подход Ламберта в действии, давайте рассмотрим один из его ранних примеров [Lam, стр. 11]. Исходя из двух утверждений $inline$a$inline$ и $inline$b$inline$, Ламбер использовал $inline$ab$inline$ для обозначения того, что у них было общего, следовательно, $inline$a-ab$inline$ представляло такие свойства $inline$a$inline$, которыми не обладало утверждение $inline$b$inline$. Интересно, что Ламберт использовал для этого фразу «eigene Merkmale», которая может быть переведена как «собственная характеристика», отсылка к префиксу «eigen-» из предыдущей статьи этого цикла. Точно так же, $inline$b-ab$inline$ представляет те свойства $inline$b$inline$, которыми не обладает $inline$a$inline$. Следовательно, выражение $inline$a+b-ab-ab$inline$ относится к собственных характеристикам $inline$a$inline$ и $inline$b$inline$, взятым вместе, которые сегодня мы называем симметрической разностью. Чтобы это сработало, обратите внимание, что $inline$+$inline$ Ламберта должен быть истолкован не как объединение, а как комбинация (с возможным повторением) $inline$a$inline$ и $inline$b$inline$. В любом случае, этому понятию был присвоен собственный символ, так что $inline$a∣b$inline$ представляет аспекты $inline$a$inline$, которые не являются общими с $inline$b$inline$, и наоборот. Это приводит к логическому уравнению $inline$a∣b + b∣a + ab + ab = a + b$inline$, которое гласит, что объединение собственных характеристик $inline$a$inline$ и $inline$b$inline$ с двумя копиями их пересечений дает тот же результат, что и объединение $inline$a$inline$ и $inline$b$inline$.
Заключение… Пока что
Как мы увидели, общие попытки в этот период заключались в том, чтобы выработать способ о логике. У Лейбница было видение — хотя и неполное — универсального исчисления, основанного на языке предикатов субъекта, Ричери использовал философский подход для классификации утверждений и доказуемости, а Ламберт ввел систему обозначений для представления логических идей. Первый и последний опирались на аналогию с арифметикой, в которой утверждения и выводы были представлены числами и операциями, соответственно. В частности, метод Ламберта напоминает раннюю диаграмму Венна в символической форме, хотя он думал о своих объектах как об объединениях, обладающих несколькими качествами, а не как наборах, обладающих несколькими элементами.
Не удивительно, что на этом история не закончилась! Спустя примерно 60 лет после попыток Ламберта систематизировать логику, Огастес де Морган написал свою «Формальную логику» (с более понятным названием «Исчисление умозаключений») с теми же целями, что и его предшественники. В этой публикации 1847 года де Морган прояснил, по крайней мере, некоторую путаницу, формализовав понятия Лейбница о «универсальном» и «частном» путем введения «количественного определения» в его исчисление. Вот фрагмент из его письма на эту тему, в котором слово «количество» используется, чтобы провести различие между универсальным и частным.

Рис. 6. Объяснение Огастеса де Моргана противоположных утверждений в математической логике в «Формальной логике» (1847). Оцифровано Archive.org по копии, принадлежащей библиотеке университета Торонто.
Пока что обратите внимание, что некоторые другие выдержки из этой книги можно найти в «Конвергенции» в качестве одного из «Математических сокровищ» Фрэнка Светца. В дальнейшем мы продолжим рассказ с более глубокого изучения работы де Моргана в «Формальной логике», с особым интересом к обозначению, которое он выбрал для количественного определения. Затем мы рассмотрим, как изыскания 19-го и 20-го веков были направлены на то, чтобы выработать «способ записи» логики. В конечном счете, развитие теории множеств оказало глубокое влияние на математическую логику, и это привело к соответствующему изменению обозначений. Подробнее об этом в следующий раз!
Источники
[Caj] Cajori, Florian. A History of Mathematical Notations, Volume II. Chicago: Open Court Publishing Co., 1928.
[DeM] De Morgan, Augustus. Formal Logic: or, the Calculus of Inference, Necessary and Probable. London: Taylor and Walton, 1847.
[Lam] Lambert, Johann. Sechs Versuche einer Zeichenkunst in der Vernunftlehre. Berlin, 1782.
[Lei] Leibniz, Gottfried Wilhelm, Dissertatio de arte combinatoria. Leipzig, 1666. Доступен перевод на английский в «Philosophical Papers and Letters» (Leroy E. Loemker, редактор, 2-е издание) 1969 года. Два изображения представлены в «Математических сокровищах».
[Par] Parkinson, G. H. R., ed. Leibniz Logical Papers. Oxford: Clarendon Press, 1966. Содержит много переводов на английский неопубликованных трудов Лейбница.
[Rah] Rahn, Johann. Teutsche Algebra. Zurich: J. J. Bodmer, 1659.
[Ric] Richeri, Ludovico. «Algebrae philosophicae in usum artis inveniendi». Melanges de philosophie et de la mathématique de la société royale de Turin. 1 (1760-61), 46-63.
[Tho] Thomson, Garrett. On Leibniz. Stamford, CT: Thomson Learning, 2001.
Автор: Юрий Богомолов






