Наверняка на хабре уже немало постов на эту тему. Тем не менее, я попытаюсь рассказать свою точку зрения на всё это…
Однажды я прочитал в интернете про троичную систему счисления и заинтересовался. Меня мучил вопрос, а нельзя использовать в основе компьютера симметричную троичную систему счисления (СС), и даже вдруг это увеличит производительность компьютера? Мне казалось, что это возможно, и я жаждал это проверить.
Информация:
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры {0,1,2}, а в симметричной троичной системе счисления знаки {−,0,+}, {−1,0,+1}.
У некоторых людей эта логика вызывает затруднения. Они говорят, например, приведите пример подобной логики в жизни.
Человек, немного подумавший над этой логикой поймет, что она более жизненна чем двоичная. Обычный пример троичной логики в жизни связан с постоянным током: ток движется в одну сторону, в другую сторону, его нет.
Дальше:
Оказалось, что симметричная троичная система счисления использовалась давным-давно для решения «задачи о гирях», использовалась в компьютере Сетунь, построенном в 50-е годы в МГУ. С 2008 года в университете « California Polytechnic State University of San Luis Obispo» функционирует цифровая компьютерная система TCA2, основанная на троичной системе счисления.
В чем же плюсы троичной СС над двоичной? Рассмотрим эти плюсы:
1.Меньше разрядов(Написано разжевано, чтобы каждый смог понять суть этого пункта)
Возьмем число 10 в десятичной СС и переведем его в двоичную СС, получим 1010, переведем в троичную симм. СС, получим +0+, ну а если в троичную несимм. СС, то получим 101. Из этого мы видим, что в некоторых числах в троичной симм. и несимм. СС-ах меньше разрядов, чем в двоичной СС.
Возьмем число 5 в десятичной СС и переведем его в двоичную СС, получим 101, переведем в троичную симм. СС, то получим +--, ну а если в троичную несимм. СС, то получим 12. Из этого мы видим, что в некоторых числах в троичной несимм. СС меньше разрядов, чем в двоичной и троичной симм. СС-ах.
2.Емкость
Троичная СС вмещает больший диапазон чисел, т.к. 3n>2n (где n-натуральное число). Например, если n=9, то 39=19683>29=512. Для доказательства были построены таблицы и диаграммы в Excel на основе таблицы расчетов.
3.Экономичность
Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p. Рассмотрим график этой функции для различных p и n, построенный с помощью Microsoft Excel.
Мы рассмотрели троичную арифметику, теперь затронем логику:
В чем же проблемы двоичной логики?
1.Мощности компьютера, основанного на двоичной логике, не всегда хватает. Приведем пример. Одна из наиболее сложных систем защиты – криптосистема RSA. Вскрытие шифра RSA с длиной ключа 1024 бита (такая длина часто используется в информационных системах) займет в лучшем случае — при проведении распределенных вычислений на тысячах мощных ПК — не менее пятнадцати лет, а к тому времени данная система шифровки перестанет быть востребованной.
Докажем математически какая система счисления будет наилучшей для максимальной мощности и емкости памяти. Для этого рассмотрим функцию f(p)=p^(n/p), в которой p – основание системы счисления, а n – количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел, которое при этом можно записать, будет равно pn/p
f(p)=p^(n/p)
Для того, чтобы определить максимальное значение функции, найдем ее производную:
ln f = ln p^(n/p)
ln f =n/p* ln p
...(Я не буду приводить здесь всю математику)
n*p^(n/p-2) никогда не будет равно 0 => (1 — ln p)=0, ln p = 1, p = e
e = 2,71, а ближайшее целое число к нему – это три.
Значит, в этом плане лучшая система с целочисленным основанием — троичная.
Самое вкусненькое — рассмотрим троичные логические операции:
1.Отрицание
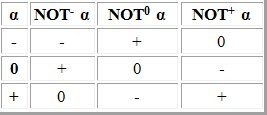
2.Конъюнкция — логическое И

3.Дизъюнкция — логическое ИЛИ
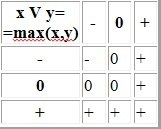
4.Операция Выбора. Эта операция существует только для троичной логики. Таблица истинности каждой из этих трёх операций содержит везде „-“, кроме единственного значения, которое ею можно выбрать.
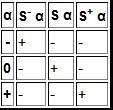
5.Модификация. Полное название этих одноместных операций: увеличение на единицу по модулю три (INC) и уменьшение на единицу по модулю три (DEC). Увеличение на единицу по модулю три – это циклическое прибавление единицы.
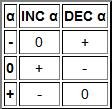
Здесь видны и прежде знакомые вам логические операции из двоичной логики, но добавились и новые…
Итог:
В конечном итоге видно, что троичная симметричная система лучше двоичной системы в некоторых показателях, но не сильно выигрывает. Но с пришествием квантовых компьютеров троичные вычисления получили новую жизнь. Универсальные квантовые логические вентили — краеугольный камень новорожденных квантовых вычислительных систем — требует сотни вентилей для завершения одной полезной операции. Квантовый компьютер канадской компании D-Wave, анонсированный в прошлом году, состоит всего из 16 квантовых битов — кубитов — минимум, необходимый для управляемого вентиля «NOT». Я думаю, если бы началось производство и тестирование таких компьютеров, то результаты были бы лучше, чем у обычных компьютеров, вскоре началось бы массовое их производство, и про двоичные компьютеры все бы забыли…
Автор: Paradoxxx








