Лента или лист Мëбиуса — верный друг всех адептов занимательной математики. Из простой бумажки можно соорудить неориентируемое гладкое двумерное многообразие, без труда вложить его в трёхмерное пространство с помощью скотча, а потом эффектно разрезать на потеху публике.
Но, серьёзно, кого сейчас можно удивить лентой Мёбиуса, да ещё на Хабре? Знаем, клеили, резали! Но всё же, я надеюсь подарить вам сегодня ещё несколько незаезженных топологических инсайтов на эту одностороннюю тему. Более того, в ней есть ещё что изучать, и помимо несложных опытов, я поделюсь с вами двумя относительно недавними исследованиями ленты Мёбиуса, опубликованными в 2010-м и 2014-х годах.
Предупреждение! Это практический пост. Предлагаемые эксперименты и наблюдения настоятельно рекомендуется провести самостоятельно, и очень желательно, — с детьми! Никакие картинки не дадут того опыта, который можно получить оперируя своими руками! А уж такой радости и подавно!
Часть 1. Эксперименты с краями
Сейчас мы заострим внимание не на сторонах ленты, о которых, кажется, сказано уже всё, что можно, а на её краях. А чтобы постичь топологию краёв чего бы то ни было, хорошо бы каким-то образом отделить край от поверхности. Это можно сделать, если вместо бумаги использовать прозрачную плёнку, например, файл для документов, а края отмечать маркером.

Итак, нам понадобятся тонкий скотч, цветные маркеры или фломастеры, ножницы либо канцелярский нож и, главный ингредиент — прозрачная плёнка.
Первые два эксперимента носят разминочный характер.
Эксперимент 0 (медитативный)
👌 С помощью указательных и больших пальцев на обеих руках, сформируйте два кольца, подобно мудре муладхара.
👌 Внимательно рассмотрите полученные кольца и нараспев произнесите слова: "тривиальное зацепление".
👌 А теперь сцепите эти два кольца так, чтобы одно проходило сквозь другое.
👌 Прочувствуйте разницу и произнесите слова: "зацепление Хопфа".
А теперь немного серьëзнее. Топология исследует такие свойства математических объектов, которые не изменяются при непрерывных преобразованиях. Если мы посмотрим на сцепленные звенья металлической цепи, то станет ясно, что без разрезания мы не сможем их разъединить, и любые непрерывные деформации (растяжения, сгибания) не освободят звенья от этого соединения. Это значит, что мы имеем дело с какой-то топологической структурой, вернее отношением между замкнутыми линиями (петлями), которое и называется зацеплением.
Простейшие из зацеплений, рассмотренные нами, буквально, на пальцах, именуются тривиальным и зацеплением Хопфа.
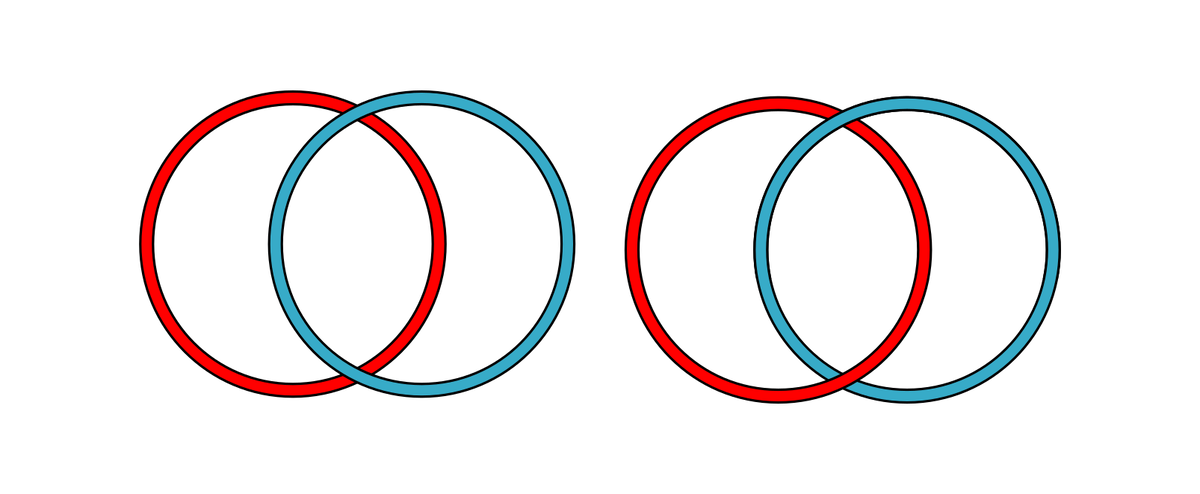
Если кольца цепи непрерывным преобразованием никак не разъединить, то для сцепленных пальцев существует преобразование, их разъединяющее. Для этого нужно использовать туловище, и голову, разумеется :) Впрочем, этот известный математический трюк сегодня нам не понадобится.
Зацепления подразумевают что петли могут как-то проходить друг в друга, что подводит нас к понятию дырки. На математическую формализацию этого понятия нужно по-хорошему, потратить ещё одну статью, и сейчас мы этого делать будем. Скажем только, что наличие одномерных дырок позволяет зацеплять друг за друга петли так, что без разрезания расцепить их и превратить в тривиальное зацепление никак не получится.
Эксперимент 1
Давайте же, наконец, резать и клеить! Начать исследование стоит с простого цилиндра, для этого склеим ленту без всяких премудростей и перекручивания. У нашего цилиндра совершенно очевидно есть два края, которые можно раскрасить разноцветными маркерами в два цвета. И эти два края образуют тривиальное зацепление.

Кстати, раскрашивать края удобнее ещё до склеивания, когда плёнка лежит плоская на столе и края видны «невооружённым глазом».
В этот момент стоит задать себе вопрос: "Сколько дырок у цилиндра?" Для ответа него, надо выяснить, как можно зацепить с его краями какую-нибудь петлю, скажем, сделанную из шнурка. Такой способ принципиально один. Даже если мы пропустим сквозь цилиндр шнурок дважды или трижды, петля при этом будет одна и проходить она будет сквозь петли, образованные краями. Так что цилиндр имеет одну (одномерную) дырку.
Эксперимент 2
Теперь склеим ленту Мëбиуса с подкрашенным краем. На прозрачной плёнке становится ясно видно, что этот край единственный. Более того, покрутив ленту в руках, можно увидеть, что этот край свёрнут в одну петлю, дважды окружающую дырку в середине ленты. Как ни крути, распрямить эту двойную петлю не получится, еë прочно «держит» дырка, не дающая гладким преобразованием превратить край в простое кольцо.

В том-то и состоит фундаментальная роль дырок в топологии — не выпускать зацепленное! Сквозь дырку ленты Мëбиуса можно пропустить шнурок и убедиться в том, что края ленты дважды огибают его, и надёжно с ним зацеплены по-хопфовски.
Нарисуем теперь маркером линию, ровно посередине полоски, лишний раз удостоверившись в том, что у нашей поверхности одна сторона. Лучше сделать это цветом, отличающимся от цвета края. Вертя результат в руках, можно увидеть, что центральная линия, в отличие от края, охватывает дырку в ленте только один раз.
А теперь внимательно посмотрите на центральную линию — она образует с линией края зацепление Хопфа. То есть одна петля проходит сквозь другую.

Поразмыслив, и поверетев ленту в руках, мы можем заключить, что край ленты Мёбиуса оказывается зацеплен с любой петлëй, которая во-первых, принадлежит ленте, а во-вторых, образует с дыркой ленты нетривиальное зацепление. Такие петли можно назвать нетривиальными внутренними петлями.
На этой анимации хорошо видно, что имеется в виду под зацеплением внутренней петли с краем листа Мёбиуса.
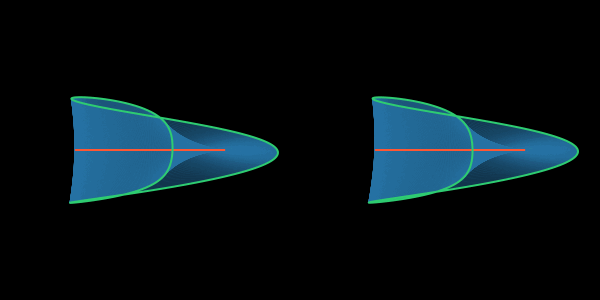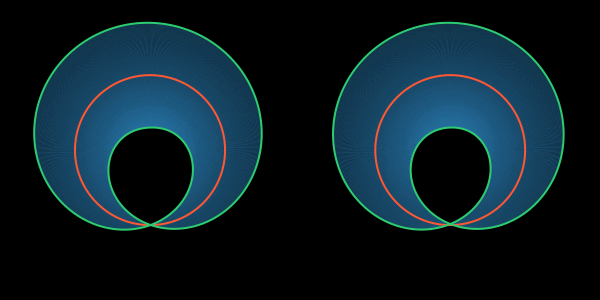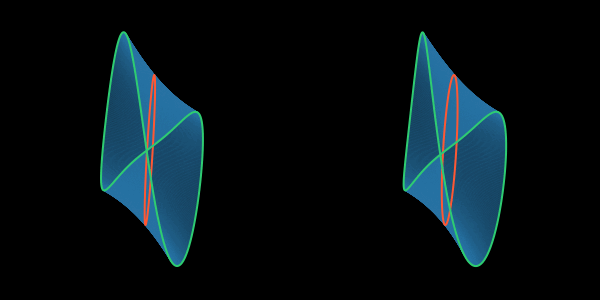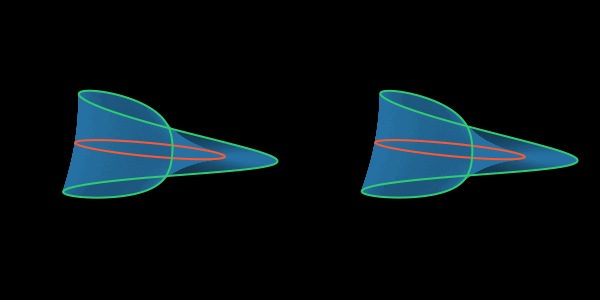
Вернитесь к цилиндру и убедитесь в том, что на нём нельзя нарисовать какие-либо внутренние петли, зацепленные друг с другом: они либо пересекаются, либо тривиально висят в воздухе отдельно друг от друга.
К чему же это приводит? Если мы станем разрезать ленту вдоль нетривиальной петли, но не пересекая её, то создадим новый край для узкой ленты Мёбиуса, а старый край при этом отделится и образует новую ленту, образующую с лентой Мёбиуса зацепление Хопфа. Если вы по какой-то причине этого ещё не делали, то проделайте непременно!
Эксперимент 3
Разрезав ленту ровно вдоль внутренней петли, нарисованной достаточно толстой линией, мы сразу получим окрашенный край получившейся поверхности. И тут же убедимся в том, что края у результата снова два, как и у цилиндра, и оба они представляют простые петли. Однако внимательно приглядевшись к линиям, «висящим в воздухе», мы можем увидеть, что эти петли оказались зацеплены друг за друга.

У цилиндра они находились рядом друг с другом, а у новой поверхности одна петля проходит сквозь другую, и никаким непрерывным преобразованием (без использования ножниц), их не расцепить.
Если задуматься об этом впервые, то кажется странным, что у непрерывной поверхности один край проходит сквозь другой край. Для того, чтобы сделать это открытие более очевидным, разрежем получившуюся ленту ещё раз по какой-нибудь внутренней петле, тем самым разъединив еë края. Результат знаком всем юным исследователям ленты Мëбиуса — мы получили две двусторонние ленты, зацепленные по Хопфу.

Эксперимент 4
Лента Мёбиуса перед склеиванием прокручивается на половину оборота. Лента, полученная разрезанием листа Мëбиуса, оказывается скрученной на полный оборот. Естественно выяснить, а что собой представляет лента, скрученная на полтора оборота и во что превращается её край.
Вырежьте, раскрасьте край и склейте такую ленту, а потом внимательно рассмотрите получившуюся линию. Можно разложить ленту на столе или вертеть в руках, главное рано или поздно осознать, что единственный край этой ленты завязан в узел. Вместо невнятной фотографии, которая толком ничего не демонстрирует, я приведу соответствующую анимацию:
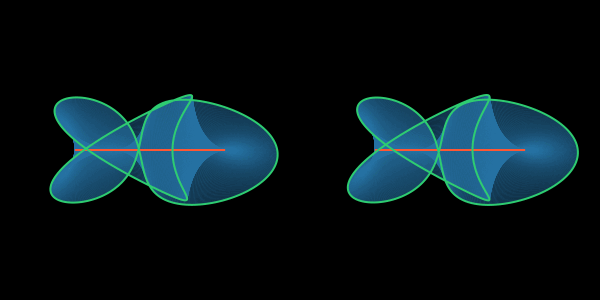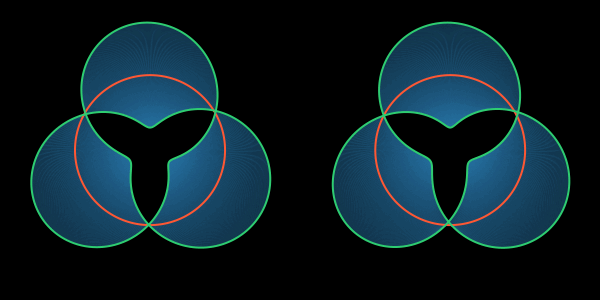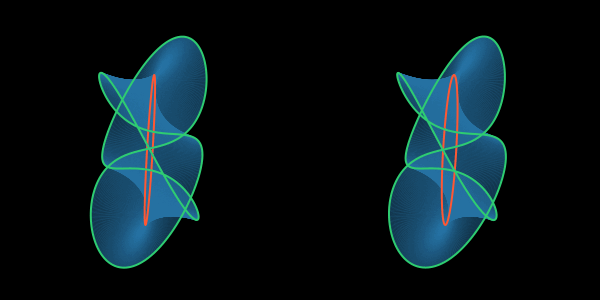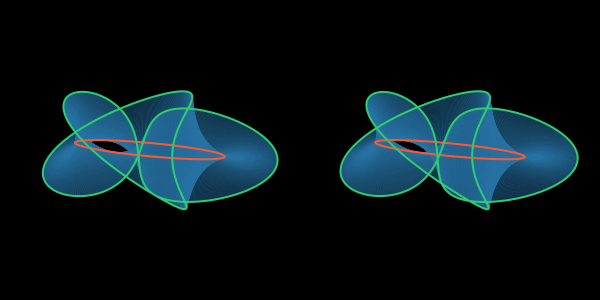
Это простейший из узлов, который в трёхмерном мире нельзя развязать не разрезая верёвки. Называется он трилистником. Лента, которая скручена трижды, заклеивает этот узел поверхностью. Разрезание такой ленты по нетривиальной внутренней петле линии должно породить две зацепленные ленты, также завязанные узлами.
Эксперимент 5 (вкусный)
А если дело происходит не в классе, а дома, то рекомендую позвать маму, приготовить с ней тугое яичное тесто. После чего можно дружно, всей семьëй исследовать топологию традиционного хвороста, который получается из полосок раскатанного теста с разрезами и всевозможными непрерывными преобразованиями.

Делая надрезы и заплетая косички, а потом соединяя противоположные стороны полосок, можно получить хворост самых разных топологий, в том числе, и мёбиусовой. Рекомендую!
Избавляемся от краëв
Передо мной на столе лежит реализация давнишней моей мечты: распечатанное на принтере вложение листа Мëбиуса с краем, принимающим форму простой петли, окружающей дырку ленты всего один раз. Эта фигура имеет даже своё название: суданская поверхность.

Она примечательна не только своей элегантной формой и тем, что делает единственность края листа Мëбиуса очевидной, самое главное еë достоинство в том, что она позволяет представить себе два способа заклеить дырку в ленте Мëбиуса.
Склеивая два листа Мëбиуса по их краям, мы получим бутылку Клейна.
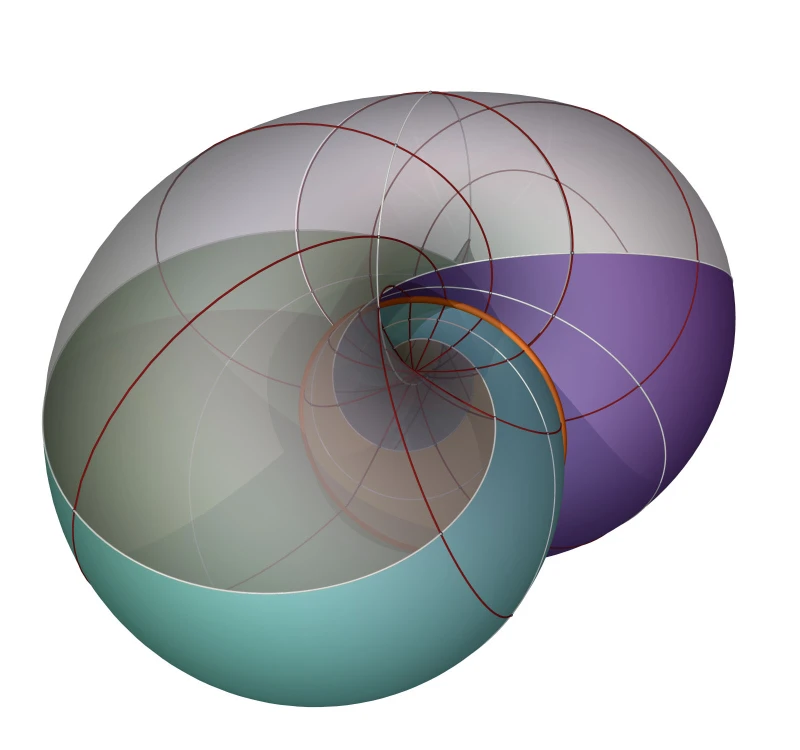
Суданская поверхность представляет собой разрез бутылки Клейна разделяющий еë на два односторонних листа. Очевидно, что приклеить две такие поверхности краями друг к другу можно только, допустив самопересечение получающейся поверхности.
Если же мы заклеим дырку в листе Мëбиуса диском, то получим менее известную среди широкой публики, но гораздо более полезную и популярную среди профессионалов проективную плоскость.
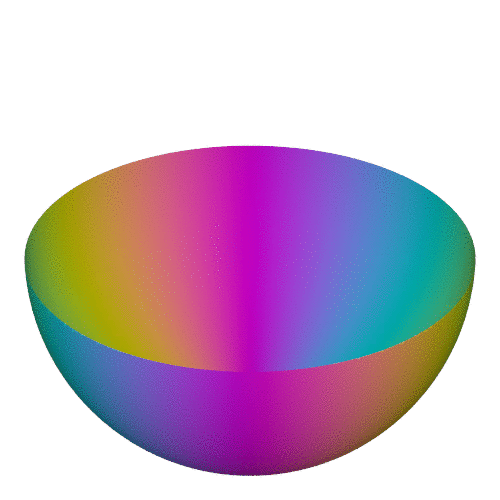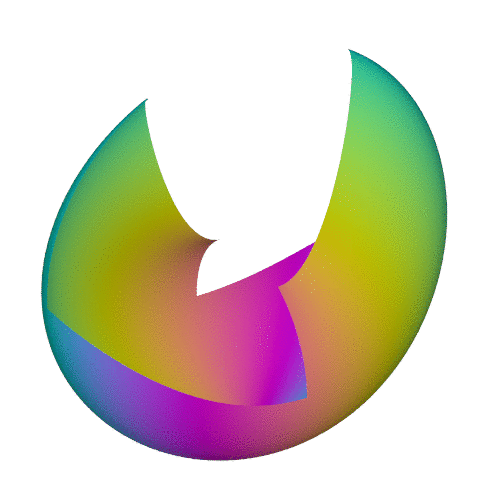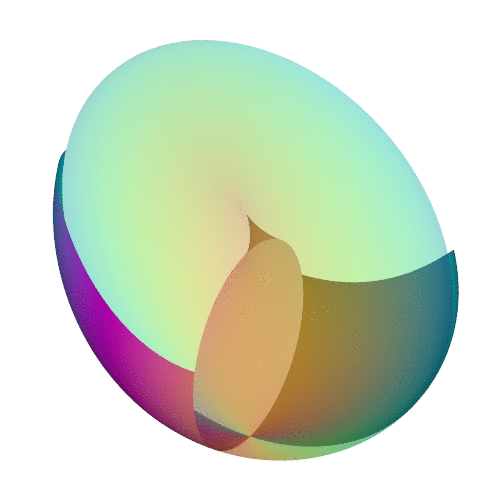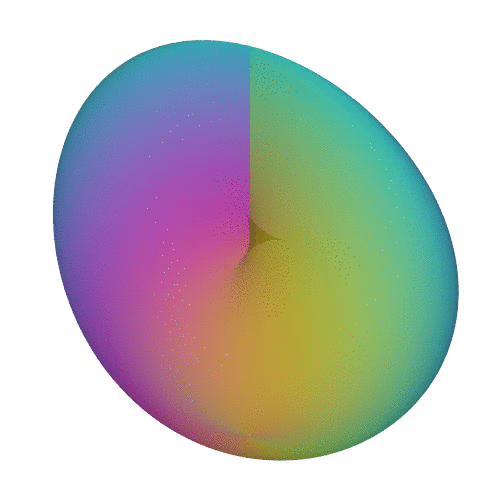
Другие анимации проективной плоскости можно увидеть тут.
И опять же, самопересечения получающейся поверхности будет не избежать. При всей свой экзотичности, геометрия на проективной плоскости имеет очень понятное нам представление в виде ровного поля с линией горизонта, при приближении к которой, видимые нами параллельные линии сближаются и пересекаются в идеальной точке.
Часть 2. Мыльная топология
Исследования краëв и заклеивающих эти края поверхностей можно продолжить, смастерив края всех перечисленных поверхностей из проволоки и заклеивая их мыльной плёнкой. Эксперимент мокрый, небыстрый, но очень увлекательный!
Как известно, мыльная плёнка решает уравнение Лапласа для заданной геометрии граничных условий, к которой сводится вариационная задача поиска минимума поверхностной энергии. Эта задача известна как задача Плато.
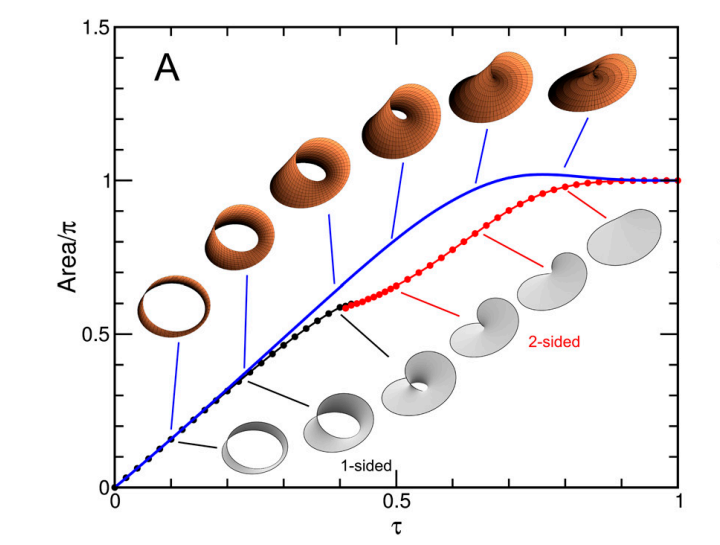
По мере изгибания проволочного края, энергия плёнки с топологией ленты Мёбиуса в какой-то момент становится равна, а потом и превышает энергию плёнки с топологией простого диска (и имеющую форму винтовой поверхности — геликоида). Это заставляет плёнку поменять топологию через бифуркацию (на видео выше это происходит в моменты 0:9 и 0:32). Однако непрерывно такой переход сделать невозможно, на то она и топология, чтобы сохраняться только при непрерывных преобразований. Так что можно ожидать, что плёнка при достижении бифуркации будет просто лопаться, но в эксперименте можно наблюдать мгновенный переход от плёнки Мёбиуса к диску, не разрушающий плёнку.
В 2010 году в журнале Applied Mathematics вышла статья Soap-film Möbius strip changes topology with a twist singularity, написанная Раймондом Гольштейном и Кейт Моффат с соавторами, посвящённая детальному исследованию такого перехода. Оказалось, что этот переход происходит через образование особой сингулярности на границе, в которой плёнка перестаёт быть гладким многообразием. Интересно, что особую роль в этом топологической бифуркации играют края и их зацепление.
Дело в том, что когда плёнка имеет форму листа Мёбиуса, то одномерное многообразие точек, находящихся на плёнке в непосредственной близости от проволоки (граница Плато, названа в честь Жозефа Плато, проводившего опыты с мыльными плёнками) образуют с проволокой нетривиальное зацепление, оборачиваясь вокруг неё, как показано на рисунке.
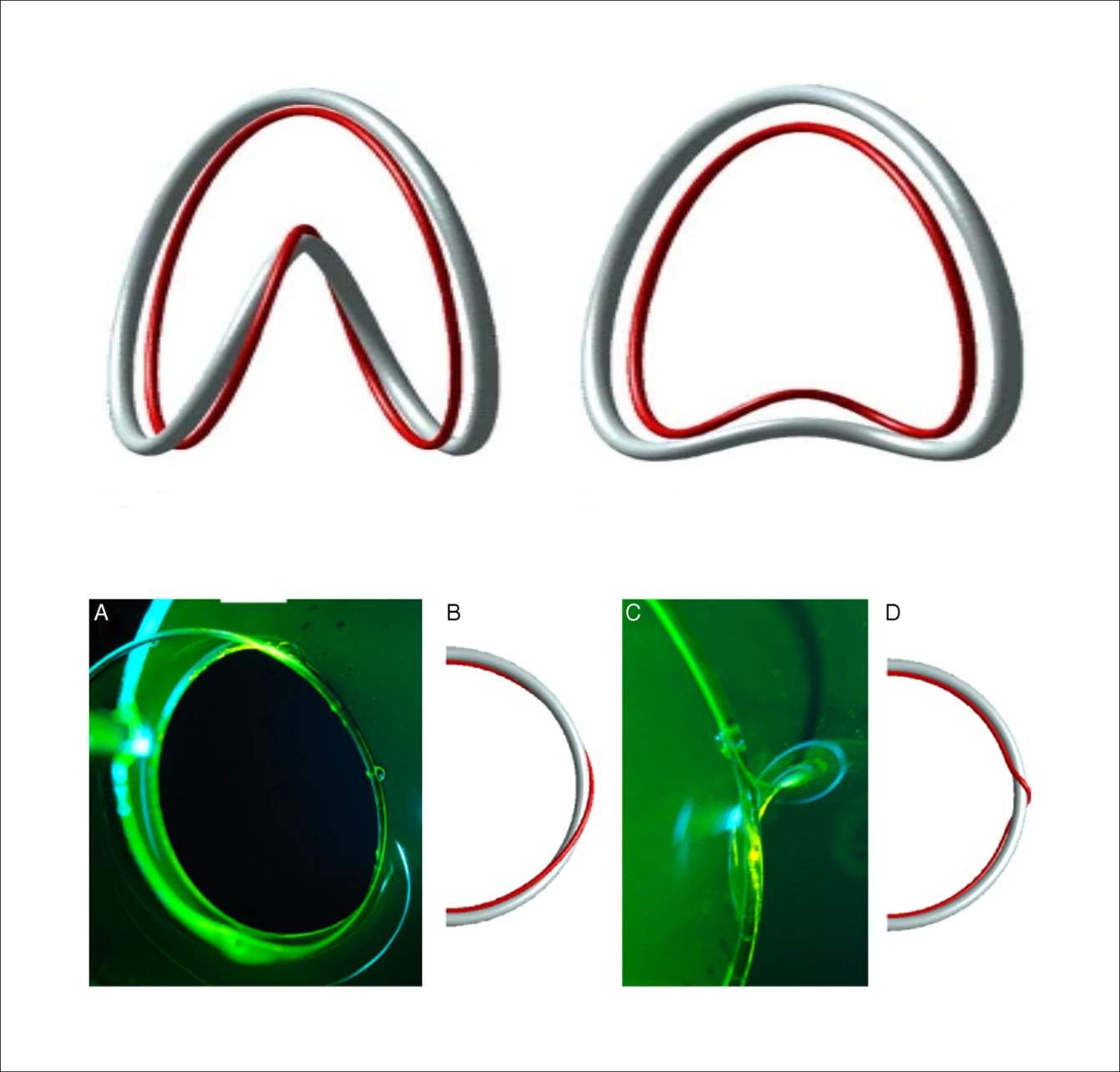
При переходе от односторонней плёнки к двусторонней это зацепление должно превратиться в тривиальное, не разрушив плёнку. Скоростная съёмка показала, что поверхностное натяжение и инерция жидкости плёнки приводят к стремительному стягиванию петли на границе Плато, окружающей проволоку.
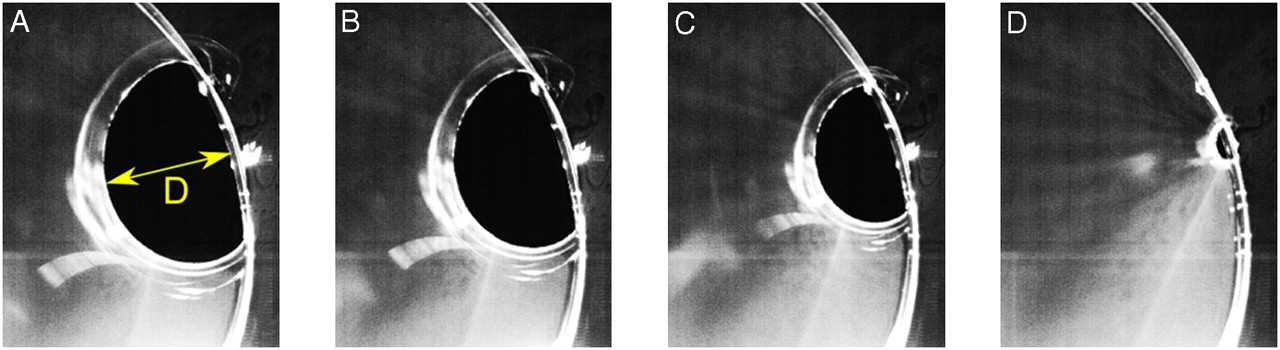
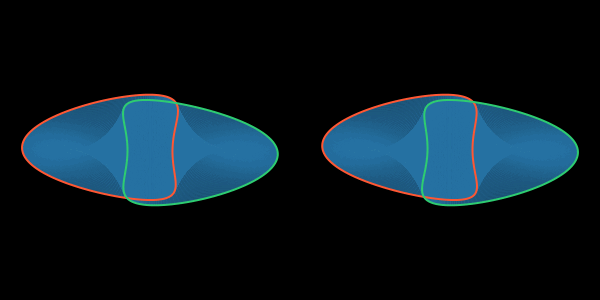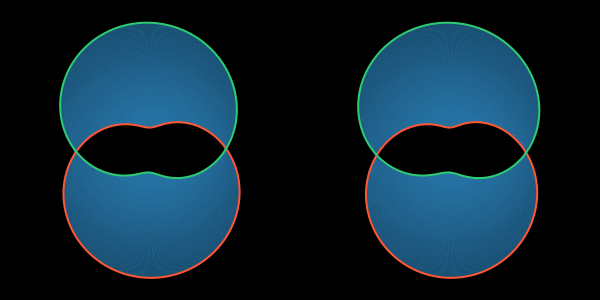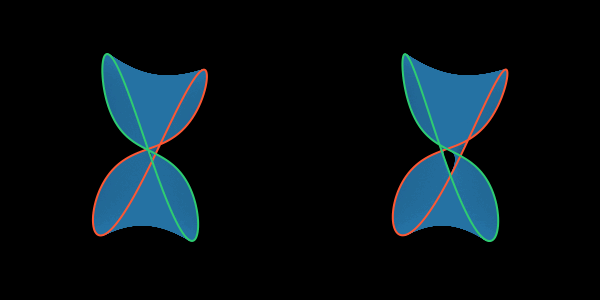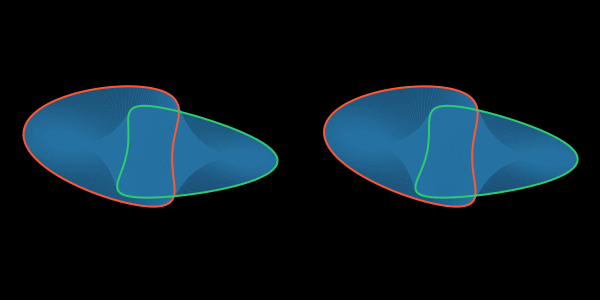
Наконец, стягиваясь, граница Плато приходит к самопересечению и превращается в «восьмёрку», у которой бо́льшая петля превращается в новую границу для двусторонней поверхности и не зацеплена с проволокой, а меньшая, зацепленная с проволокой уменьшается до предела и «растворяется», становясь частью поверхности плёнки.
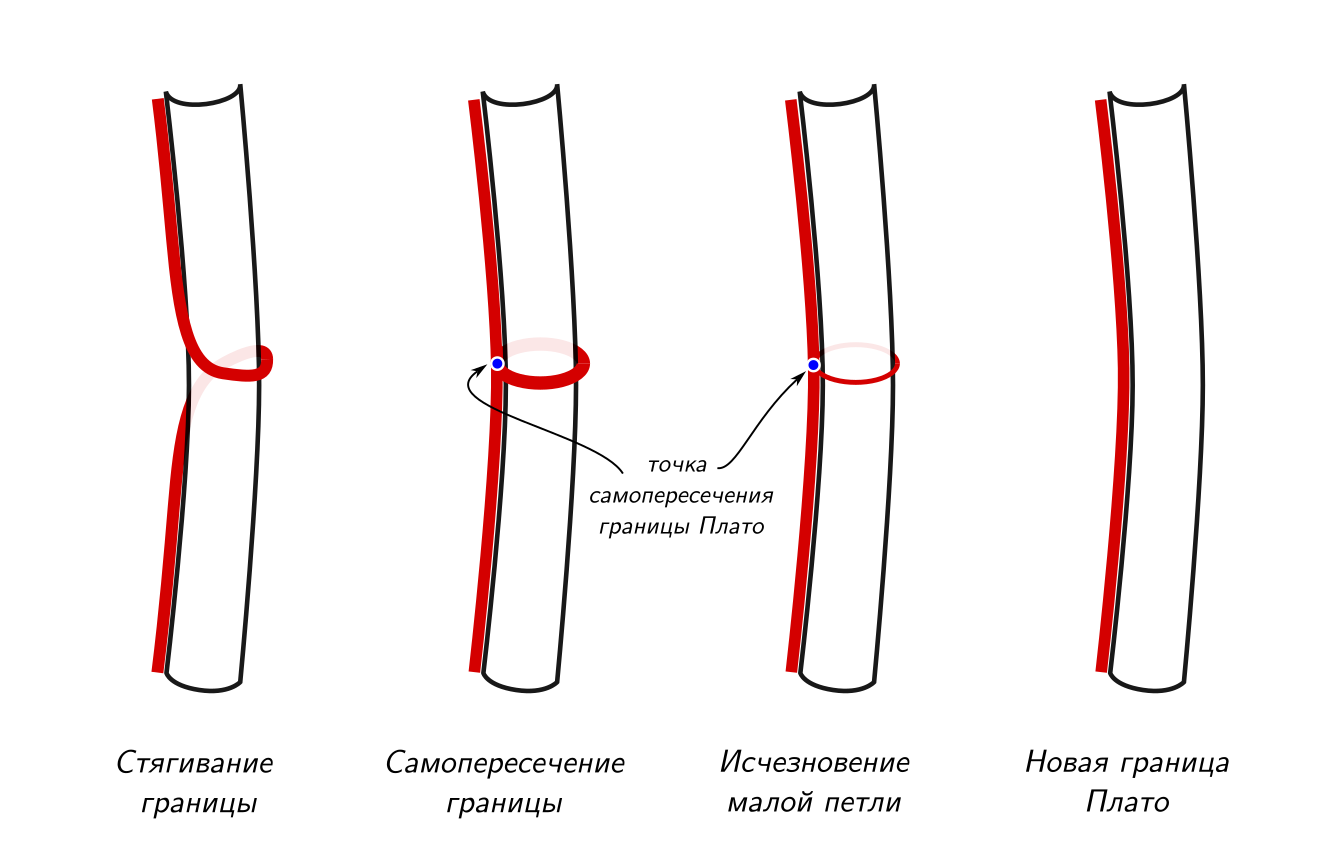
Этот переход, обеспечивая минимизацию поверхностной энергии плёнки, заставляет плёнку отойти от правильной геометрии линейчатых поверхностей, которыми хорошо описываются исходное и конечное состояния плёнки вдали от сингулярности.
Часть 3. Односторонняя статья
— Вот статья, напечатайте её, но только на одной страничке, пожалуйста.
— Хорошо! Вот вам одна единственная страничка. Не лист, заметьте, а именно страница, то есть, сторона листа. А другой стороны у неё нет. Пользуйтесь услугами нашей типографии "Топографыч"!

У бумажного листа две стороны, каждую из которых мы называем страницами. Так что напечатать книгу или документ можно с произвольным числом листов, но только с чётным числом страниц. Электронный документ, будучи в известной степени абстракцией, запросто может занимать и одну, и три, и пять страниц, однако, при печати документа с нечётным числом страниц, чётная страница всё равно добавится, хоть и останется белой.
Для того, чтобы напечатать истинный одностраничный документ, я напечатал текст этого раздела на ленте Мёбиуса. Для этого пришлось сверстать текст в две достаточно узкие колонки, воспользоваться двусторонней печатью и склеить ленту с поворотом.
Не составляет труда свернуть одностороннюю ленту из длинного и узкого бумажного листа. Но чем шире становится лента-заготовка, тем сложнее её свернуть, а начиная с какой-то ширины это будет сделать попросту невозможно. При попытке свернуть такой широкий лист, бумага либо порвётся, либо не позволит ленте сделать необходимые пол-оборота, потому что она практически не растягивается.
Возникает чисто математический вопрос: какое соотношение сторон может иметь бумажная лента, пригодная для сворачивания из неё ленты Мёбиуса?
Бумажный лист нерастяжим, а это значит, что его можно свернуть только в развёртываемую поверхность. Последнее утверждение выглядит тавтологией: "свернуть можно только то, что можно развернуть", но дело в том, что в дифференциальной геометрии развёртываемость определяется через локальные свойства поверхности, так что выяснить развёртываема поверхность или нет, можно глядя на свойства поверхности в отдельных точках, либо исследуя описывающее её уравнение, не пытаясь заниматься оригами. Это полезно при проектировании сложных форм кораблей или зданий, поскольку, если их можно представить, сшитыми из разных развëртываемых поверхностей, то изготовить их можно из изначально плоских металлических листов.
Примерами развёртываемых поверхностей могут быть всевозможные цилиндры, конические поверхности, экзотические олоид, сферикон, а так же поверхности, образованные касательными к гладким кривым. Но не всякое вложение поверхности Мёбиуса в трёхмерное пространство будет развёртываемым, так что сегодня мы посмотрим на то, какими могут быть развёртываемые, но не типичные односторонние поверхности.
Несложно провести эксперимент с настоящей бумажной лентой, сворачивая её всё туже и туже, до тех пор пока она не превратится в два конуса, которые при дальнейшем уменьшении длины ленты, начнут сплющиваться и сворачиваться в плотный кулёк, как показано на рисунке:
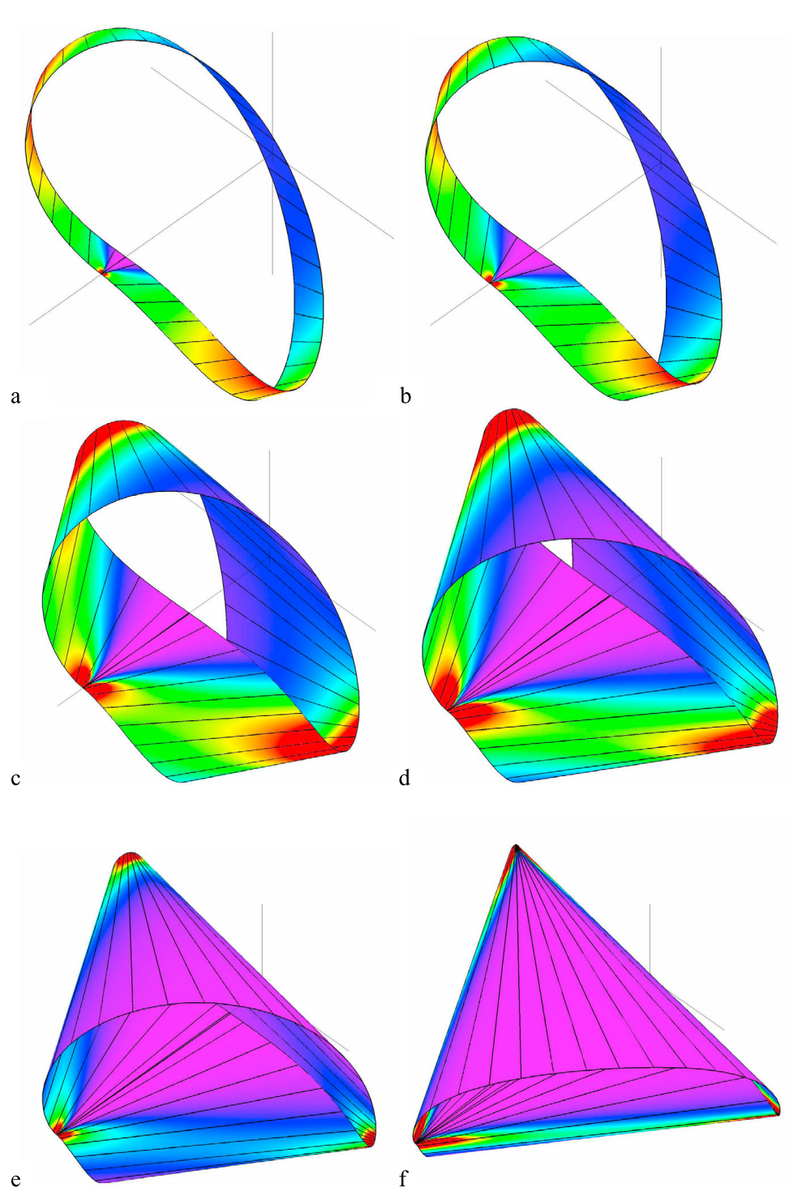
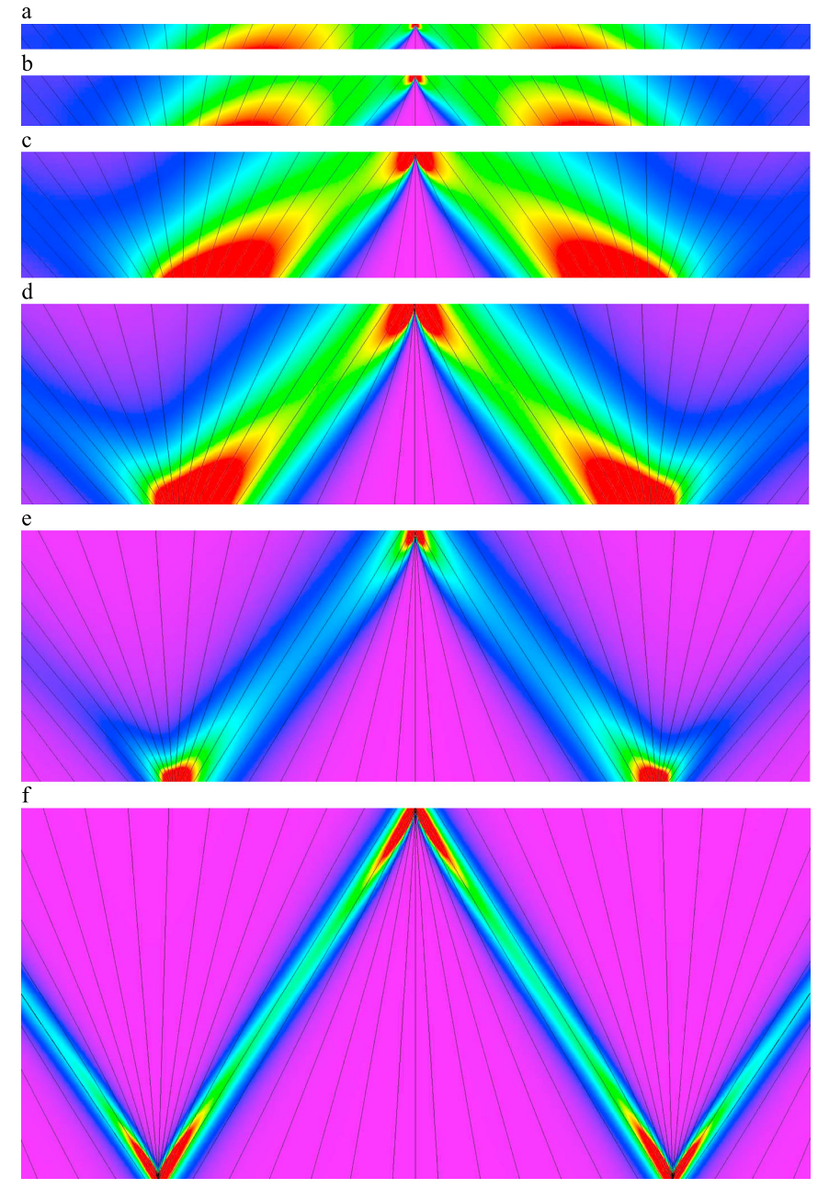
Эти иллюстрации я взял из статьи Старостина и ван дер Хейдена, вышедшей в 2014 году, и посвящённой сворачиванию различных поверхностей из нерастяжимой ленты: Equilibrium Shapes with Stress Localisation for Inextensible Elastic Moebius and Other Strips
Предельной формой ленты Мёбиуса будет сложенный втрое равносторонний треугольник, имеющий такую развёртку:
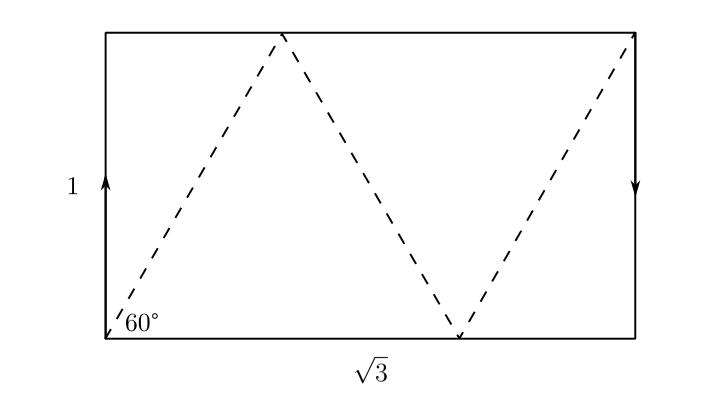
Получается, что в отличие от формата A4, имеющего отношение сторон равным , максимально широкая традиционная бумажная лента Мёбиуса может быть сложена из листа с пропорциями
. Правда, если напечатать текст, используя двустороннюю печать на принтере, и склеить такую максимально компактную одностороннюю статью, прочесть её уже не получится: она будет выглядеть, как плотно сложенный треугольник.
Чуть более читабельный вариант можно получить из ленты с пропорциями , сплющив её так, как показано не рисунке:
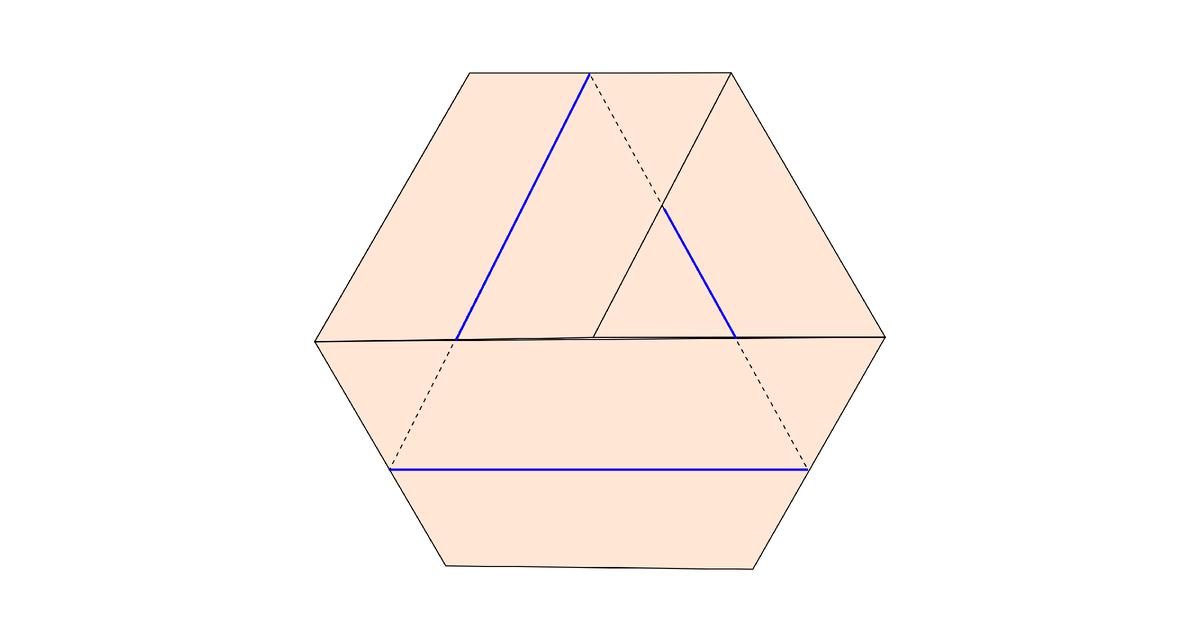
А если не ограничиваться прямоугольными лентами, то вариантов развёртываемых односторонних поверхностей станет куда больше:
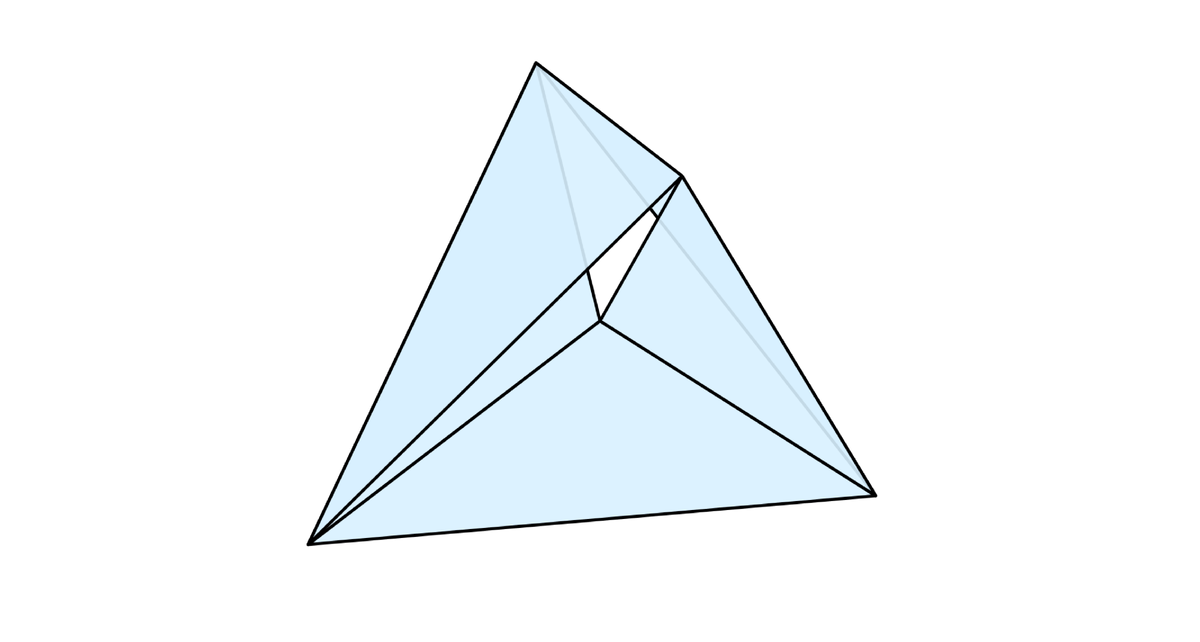


Более того, я придумал как сформировать развёртываемую одностороннюю поверхность из произвольного прямоугольного листа:
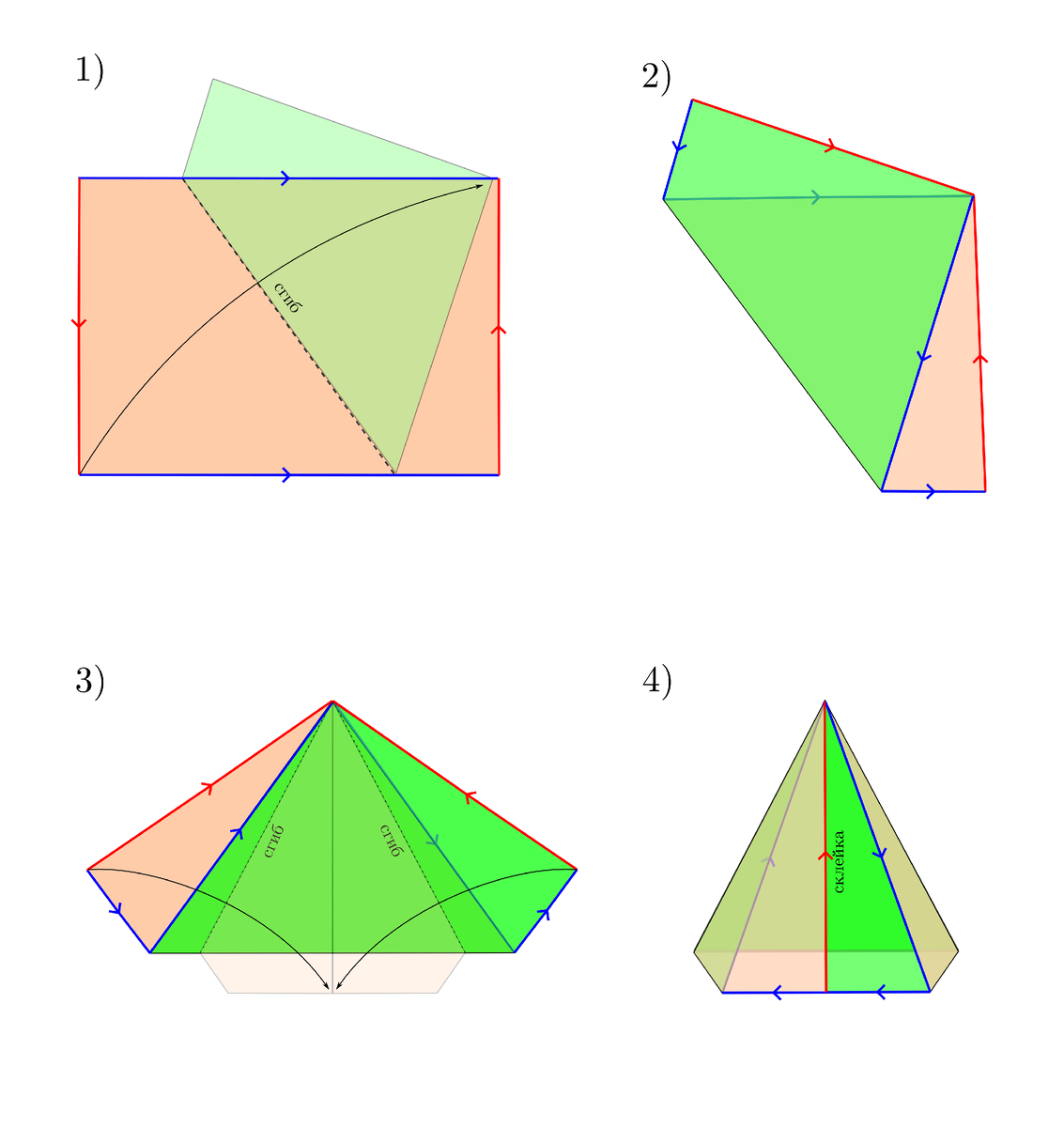
Если проследить за тем, как склеиваются стороны прямоугольника, то становится видно, что в результате мы получили одностороннюю поверхность с единственным краем, показанным синей линией. Стороны прямоугольника, показанные красной линией, отождествляются при склейке, имея противоположную ориентацию. Впрочем, такое вложение листа Мёбиуса, и лентой-то не назовёшь.
Обратите внимание на то, что край листа, показанный синей линией, имеет форму простого плоского замкнутого многоугольника. Обычно, при изготовлении одностороннего листа из бумажной ленты, получается край, делающий в пространстве две петли вокруг дырки. В предложенном вложении дырка исчезает (сжимается в точку), превращаясь в сингулярность. И через эту сингулярность неизбежно должен проходить и единственный край нашей односторонней поверхности.
Поэкспериментируйте с этим способом с помощью цветной бумаги для оригами. Свернув и склеив эту поверхность, разрежьте её по линии, перпендикулярной линии склейки, и посмотрите во что превратится эта поверхность.
Часть 4. Будет крутиться, или не будет?
Напоследок, рассмотрим ещё один нехитрый этюд на одностороннюю тему. Есть хороший маткружковский вопрос: если соединить друг с другом несколько шестерëнок, сможет эта система крутиться, или застрянет, как на знаменитой картинке.

Эта задачка красиво вводит в теорию графов, показывая зачем они нужны и что позволяют сделать. Сколь бы сложной ни была плоская система одинаковых зубчатых колёс, её можно представить в виде графа с узлами, соответствующими шестерёнкам, и рёбрами, показывающими кто из них с кем соприкасается.
Шестерёнки крутятся только в том случае, если два касающихся друг с другом колёсика вращаются в разные стороны. Если раскрасить чёрным и белым цветом узлы шестерёнок, которые вращаются, соответственно, по часовой стрелке, и против часовой, то условием подвижности всей системы, будет возможность раскрасить все узлы графа в два цвета так, чтобы для любого ребра узлы на разных его концах имели разный цвет. Если такая раскраска возможна, граф называется двудольным.
Любые деревья, то есть, графы без циклов, ничто не мешает раскрасить нужным образом. Проблемы могут возникнуть из-за циклов. Можно показать, что раскрасить двумя красками весь граф можно только если в нём все циклы имеют чётное число узлов. В противном случае раскраска невозможна, и систему шестерёнок заклинит.
Раскрашивание графа с детьми само по себе интересное занятие. Интересно решать обратную задачу: строить систему шестерёнок по произвольному графу. Подумайте, каким плоским шестерёночным системам соответствуют двудольные графы, в виде рёбер правильных куба и ромбододекаэдра?
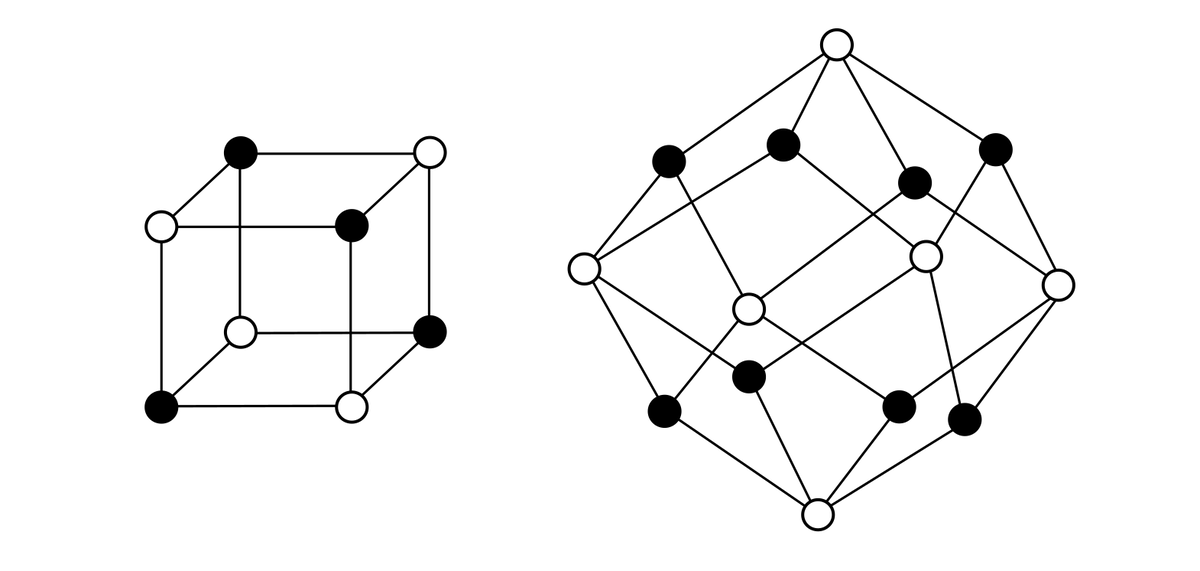
Варианты таких систем
Решение дают планетарные системы, в которых одна из шестерёнок окружает прочие. Поскольку здесь используются колёсики разного радиуса, кроме корректного графа теперь становятся важными передаточные числа шестерней.
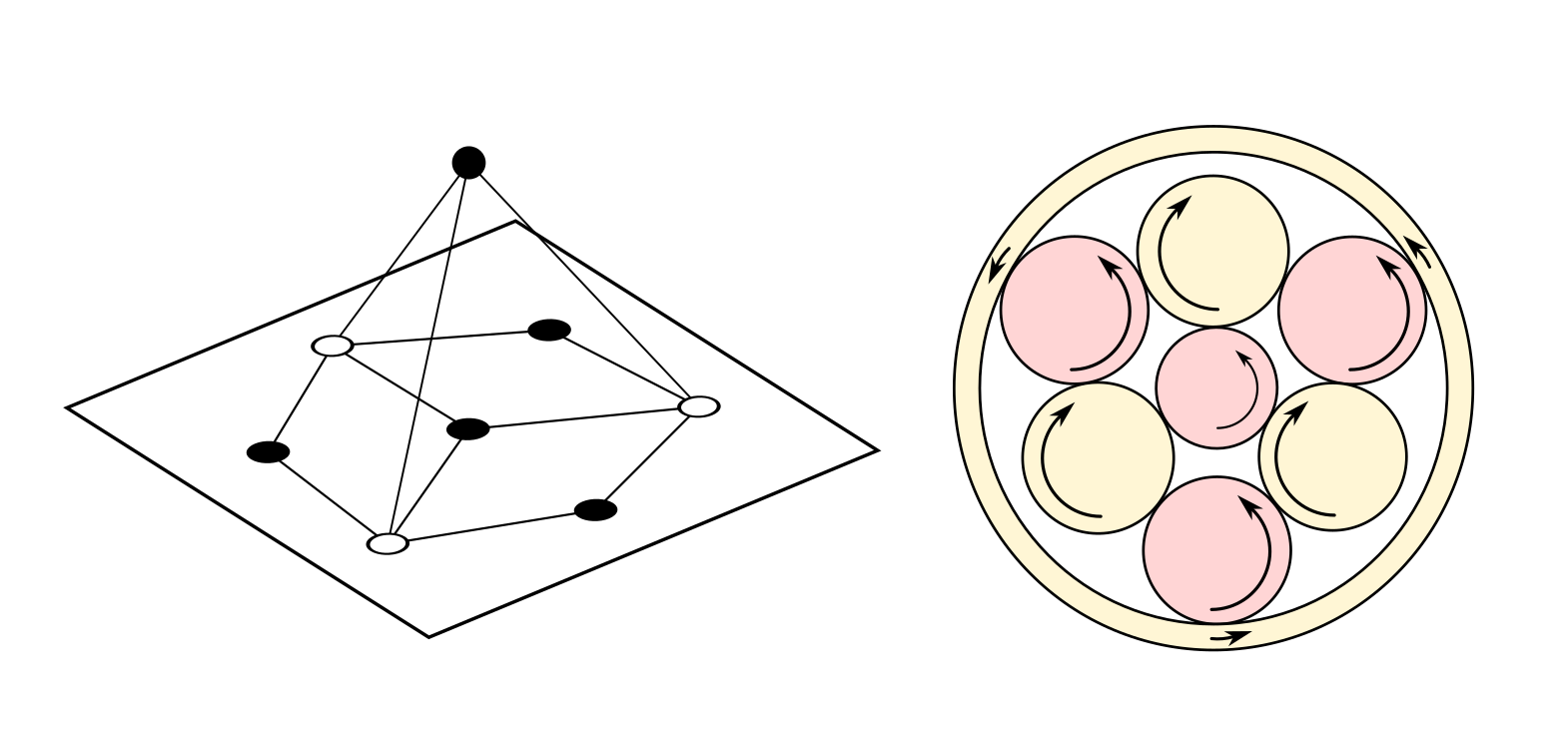
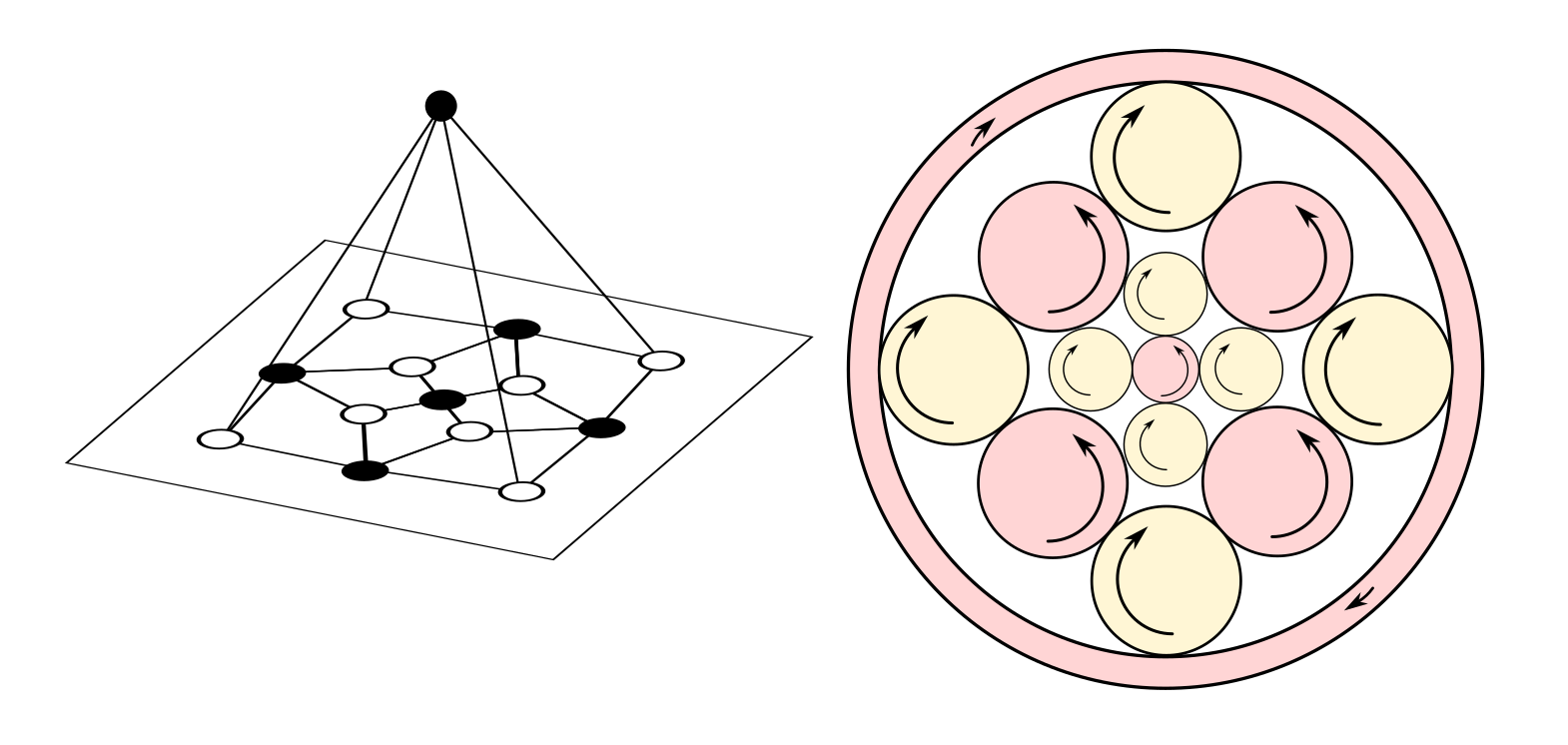
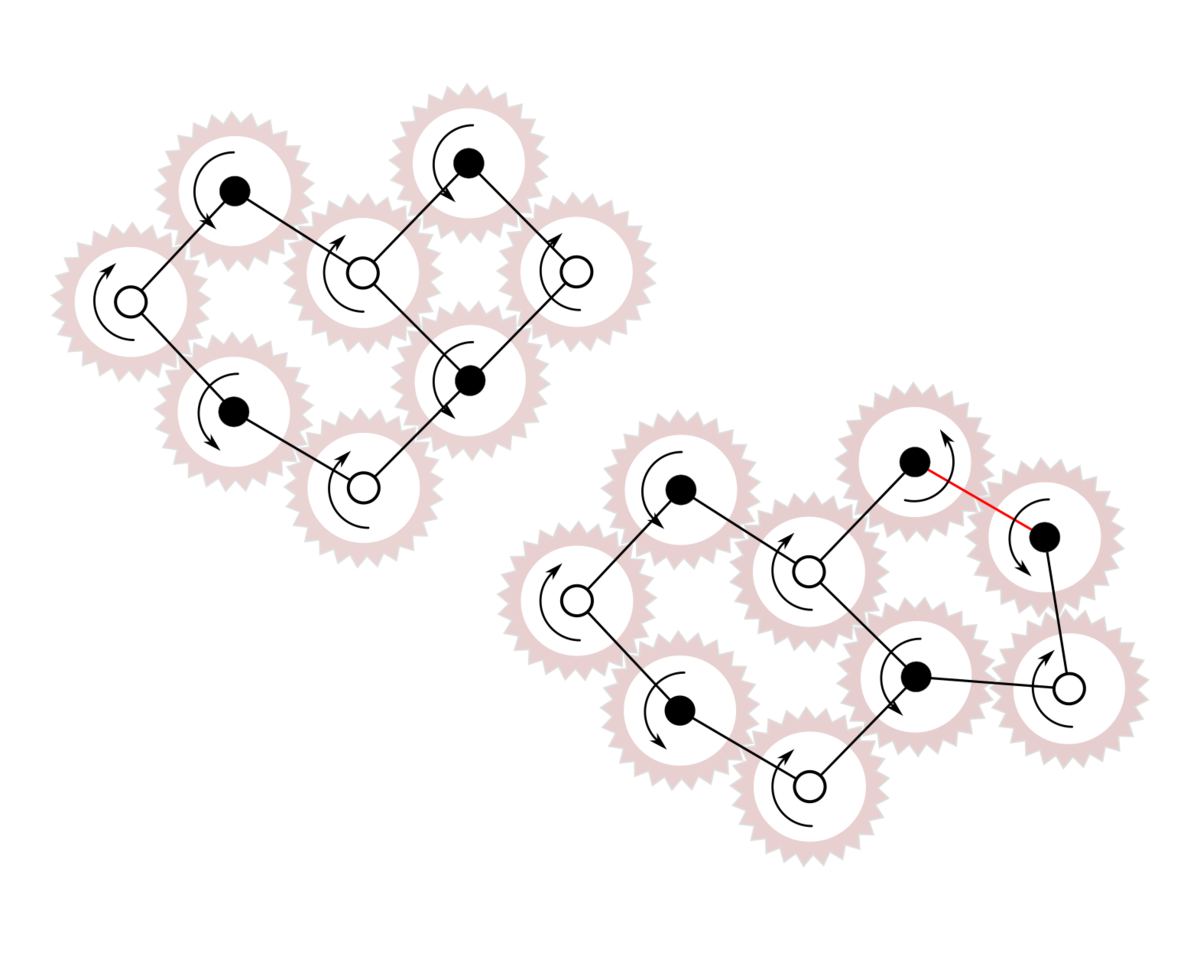
Впрочем, есть одна хитрая возможность обмануть двудольность графов и построить замкнутый цикл из нечётного количества шестерёнок, воспользовавшись вложением в трёхмерное пространство. У вращения в нашем трёхмерном мире есть одна любопытная особенность: при отражении в зеркале или переворачивании колеса, направление вращения меняется на противоположное.
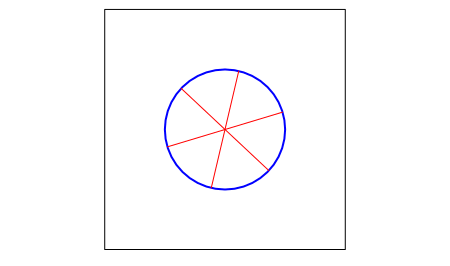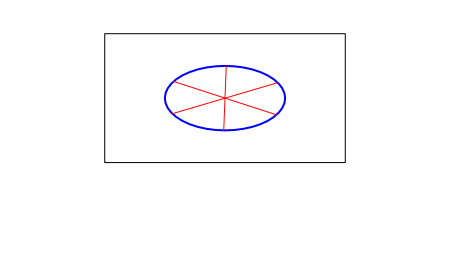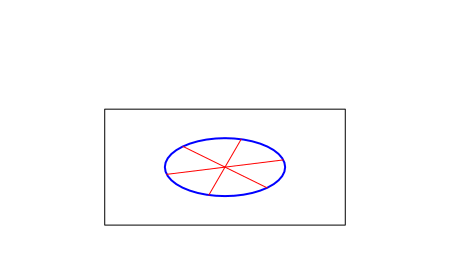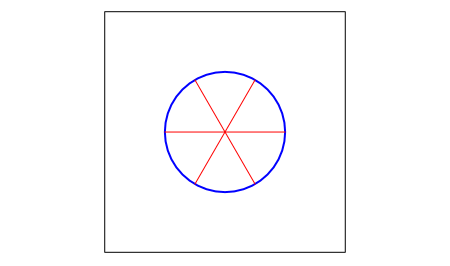
Для шестерёночных систем на плоскости это свойство никакого значения не имеет, просто отражение или переворачивание поменяет цветами чёрные и белые узлы. А что если шестерёнки расположить не на плоскости, а на ленте Мёбиуса?
Половина поворота, которую мы делаем, когда склеиваем ленту, не сможет изменить цвета узла, но может поменять направление вращения шестерёнки. Таким образом, нам удастся закрутить на ленте Мёбиуса произвольное нечётное число шестерёнок, например, 13 штук!

Я уверен, что время, проводимое с нашими детьми, направленное на совместное исследование нашего мира, составляет самые ценные моменты жизни. Математика может быть ничуть не хуже прогулки в парке. Наслаждайтесь!
Автор: Сергей Самойленко





