Задача про электрон в идеальном бесконечном кристалле

Здравствуйте, друзья!

Согласно законам квантовой механики, электрон в изолированном атоме может находиться только на определенных дискретных энергетических уровнях. Однако, когда атомы объединяются в периодическую кристаллическую решетку, ситуация меняется: вместо отдельных уровней возникают разрешенные и запрещенные энергетические зоны.

Как образуются зоны? Разобраться в этом поможет квантовая механика!

Постановка задачи

Рассмотрим предельный случай модели Кронига-Пенни. Пусть потенциал, создаваемый одномерной решёткой имеет вид:

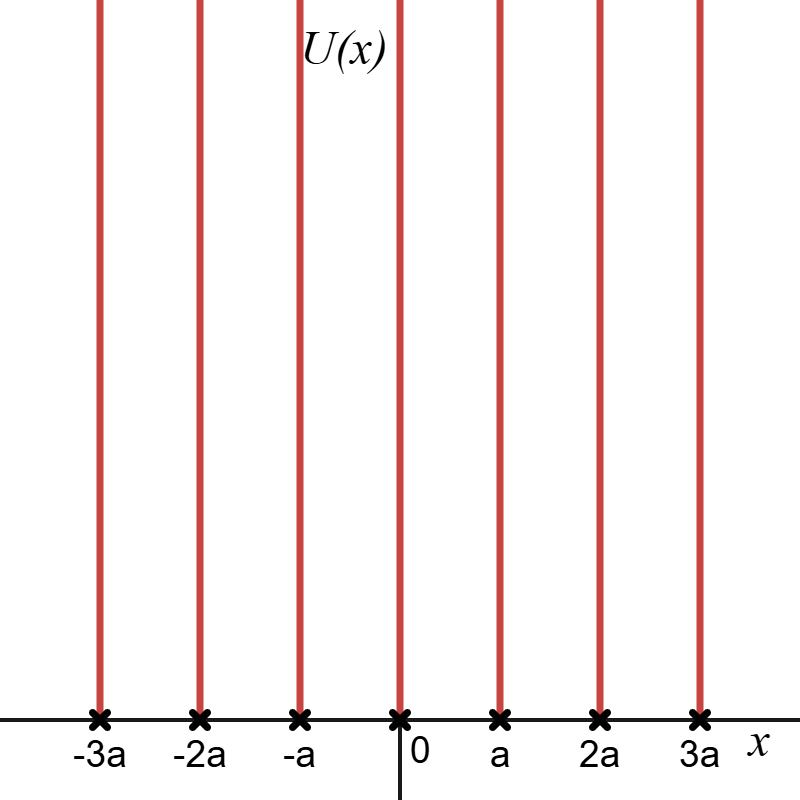
Нужно найти энергетический спектр и отвечающий ему волновые функции. Для этого нужно решить следующее стационарное уравнение Шрёдингера:

Но в каком виде искать решение?

Трансляционная симметрия. Теорема Блоха

Нетрудно заметить, что если данную систему сместить на величину кратную а, то система перейдёт сама в себя. Это так называемая трансляционная симметрия. Данному преобразованию отвечает оператор трансляции, имеющий вид:

Также нетрудно показать, что данный оператор коммутирует с оператором Гамильтона системы, а значит можно найти общие собственные функции для обоих операторов. Данный факт упрощает поиск решения, вид которого примет:

Где первую функцию выберем в качестве собственной оператора трансляции, а вторая функция будет иметь периодику потенциала.

Предлагаю найти собственные функции оператора трансляции, решив следующее уравнение на поиск собственных функций и значений оператора:

Получили функциональное уравнение Коши, решение которого известно:

Данная функция отвечает собственному значению:

Возвращаясь к исходной задаче, решение уравнения Шрёдингера будем искать в виде:

Мы получили функцию Блоха. В 1928 году физик Феликс Блох сформулировал теорему, в которой установил вид волновой функции в периодическом потенциале.

Решение уравнение Шрёдингера

Перейдём к непосредственному отысканию волновых функций, подставим установленный вид решения в уравнение Шрёдингера и получим новое уравнение на функцию u(x), рассмотрим его в области -a<x<0:

А его решение:

Тогда волновая функция в этой области примет вид:

Очевидно, что в области 0<x<a решение будет иметь такой же вид:

Но как связать коэффициенты A и B из этих областей? Подействуем оператором трансляции на решение из 1-й области, но тогда оно должно совпадать с решением из 2-й области:

Из данного условия и получаем связь коэффициентов:

Тогда волновая функция во 2-й области принимает вид:

Теперь нужно "сшить" полученные решения в точке x=0:

Подробно останавливаться на получении условий сшивки не буду.

Получаем однородную систему линейных уравнений относительно А и B, нетривиальное решение которой существует при равенстве определителя нулю:

Получили трансцендентное уравнение на энергетический спектр.

Квазиволновой вектор и энергетические зоны

Находя собственные функции оператора трансляции и решая уравнения Шрёдингера, мы пока не задумывались над физическом смыслом введённой постоянной k. Взглянув на вид Блоховских функций, можно сделать вывод, что постоянная k описывает распространение плоской волны с волновым вектором k. В физике твёрдого тела данный вектор носит название квазиволнового.

Чем же он отличается от обычного волнового вектора? Ответ кроется в полученном выше уравнении на энергетический спектр. В отличие от обычного волнового вектора, квазиволновой определён неоднозначно. Действительно, если к произведению ka прибавить 2π, то полученное уравнение не изменится, и совсем другому значению квазиволнового вектора отвечает тот же спектр энергий, а значит состояния с волновыми векторами k и k+2π/a физически эквивалентны. Для удобства значение k полагают: -π/a<k<π/a. Такое определение исчерпывает физически неэквивалентные состояния.

Перейдём к изучению полученного уравнения на энергетический спектр. Для начала продемонстрирую приведённую зонную схему - зависимость энергии от квазиволнового вектора, которая получается из данного уравнения.

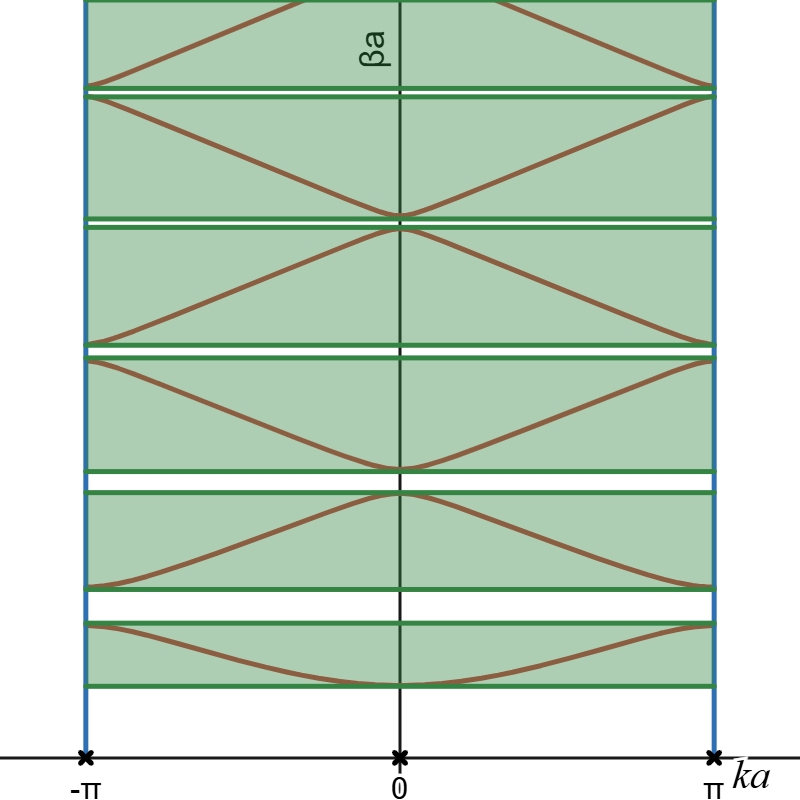
Видно, что существуют чередующиеся зоны разрешённых и запрещённых энергий.

Рассмотрим следующие интересные случаи полученного уравнения:

1) α = 0

В этом случае решение уравнения Шрёдингера в точности совпадает с решением для свободной частицы, запрещённых зон нет, разрешённые зоны заполняют все значения энергии от 0 до ∞.

2) βa >> 1

В этом случае вторым слагаемым в левой части можно пренебречь. Разрешённые зоны при таких энергиях расширяются, а запрещённые наоборот сужаются.

3) βa<<1 и ka<<1

Данный случай описывает частицу у дна разрешённой зоны, а дисперсионное уравнение принимает вид:

Откуда находим энергию:

Полученный закон дисперсий схож с законом для свободной частицы, что указывает на то, что электрон с такой энергий движется "свободно" по кристаллу с импульсом p, но обладает массой m* отличной от массы свободного электрона.

В этом случае величину p = ℏk называют квазиимпульсом, а m* - эффективной массой.

Заключение

Изложенное выше решение наглядно показывает, как в кристаллах формируются энергетические зоны.

Стоит отметить, что полученные волновые функции ненормируемые, а значит состояния отвечающие им физически нереализуемые. Действительно, ведь в природе не существует бесконечных идеальных кристаллов) Однако данная проблема разрешается введением периодических граничных условий, то есть если кристалл имеет длину L, то волновая функция на левой и правой границах должна совпадать. В это случае квазиволновой вектор принимает уже дискретный набор значений.

Статья подготовлена сообществом.