Распознавание изображений — классический пример использования нейронных сетей. Вспомним, как происходит процесс обучения сети, в чем возникают сложности и зачем в разработке использовать биологию. Подробности под катом.
В рассказе нам поможет Дмитрий Сошников — технический евангелист Microsoft, член Российской ассоциации искусственного интеллекта, преподаватель функционального и логического программирования ИИ в МАИ, МФТИ и ВШЭ, а также наших курсов.
Представьте, что у нас есть множество картинок, которые нужно отсортировать по двум стопкам с помощью нейронной сети. Каким образом это можно сделать? Конечно, все зависит от самих объектов, но мы всегда можем выделить какие-то особенности.
Нам нужно знать как можно больше информации о входных данных и учесть их на вводе вручную, еще до обучения сети. К примеру, если у нас задача обнаружить на картинке разноцветных котов, будет важен не цвет, а форма объекта. Когда мы избавимся от цвета, перейдя к черно-белому изображению, сеть научится куда быстрее и успешнее: ей придется распознавать в несколько раз меньше информации.
Для распознавания произвольных объектов, к примеру котиков и лягушек, цвет очевидно важен: лягушка зеленая, а коты — нет. Если мы оставляем каналы цвета, для каждой палитры сеть учится заново распознавать объекты изображения, потому что этот канал цвета подается на другие нейроны.
А если мы хотим разрушить известный мем про котов и хлеб, научив нейронную сеть обнаруживать животное на любой картинке? Казалось бы, цвета и форма приблизительно одинаковая. Что тогда делать?
Банки фильтров и биологическое зрение

С помощью разных фильтров можно выделять различные фрагменты изображения, которые затем обнаруживать и исследовать в виде отдельных свойств. Например, подавать на вход традиционному машинному обучению или нейросетям. Если нейросеть имеет дополнительную информацию о структуре объектов, с которыми она работает, то качество работы возрастает.
В области машинного зрения наработаны банки фильтров — наборы фильтров для выделения основных особенностей объектов.
Похожая «архитектура» используется и в биологии. Ученые считают, что человеческое зрение не определяет все изображение целиком, а выделяет характерные особенности, уникальные черты, по которым и идентифицирует объект. Соответственно, для быстрого и корректного распознавания объекта можно определить максимально уникальные черты. К примеру, у котов это могут быть усы — веерные горизонтальные черточки на изображении.
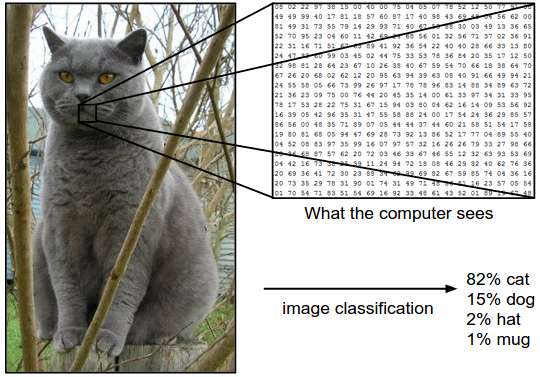
Разделение весов (Weight Sharing)
Чтобы сети не приходилось отдельно учиться распознавать котиков в разных частях картинки, мы «разделяем» веса, отвечающие за распознавание, между различными фрагментами входных сигналов.
Это требует специализированной архитектуры сети:
- сверточные сети для работы с изображениями
- рекуррентные сети для работы с текстом / последовательностями
Нейронные сети, эффективно использующиеся в распознавании изображений, в которых применяются специальные свёрточные слои (Convolution Layers).
Основная идея заключается в следующем:
- Используем weight sharing для создания «фильтрующего окна», пробегающего по изображению
- Примененный к изображению фильтр помогает выделить фрагменты, важные для распознавания
- В то время как в традиционном машинном зрении фильтры конструировали вручную, нейросети позволяют нам сконструировать оптимальные фильтры с помощью обучения
- Фильтрацию изображения можно естественным образом совместить с вычислением нейронной сети
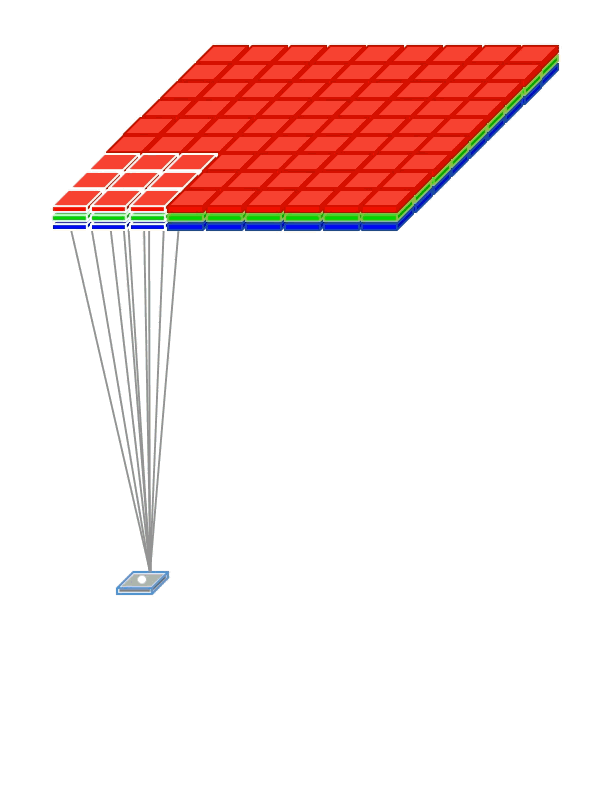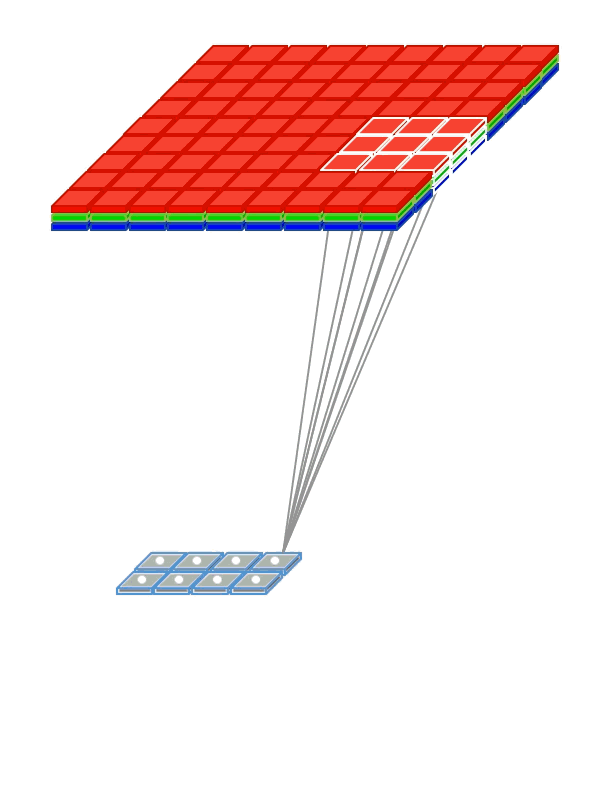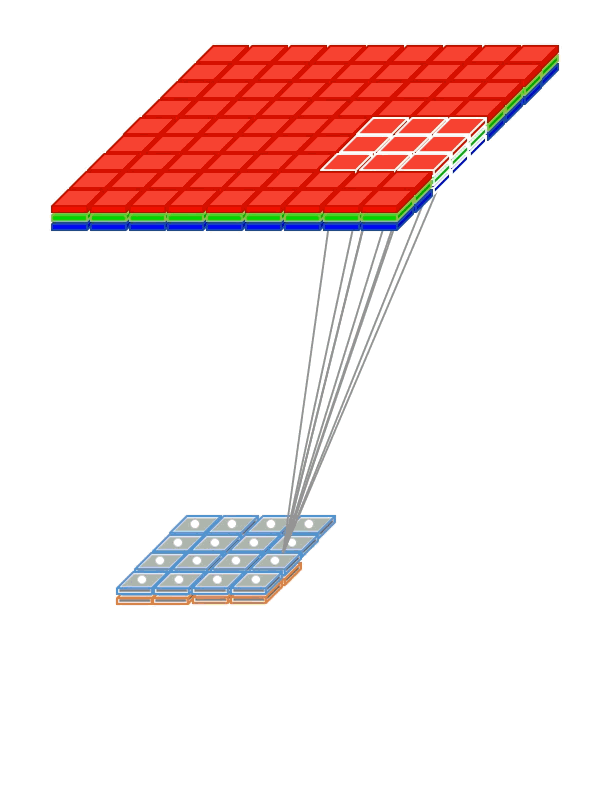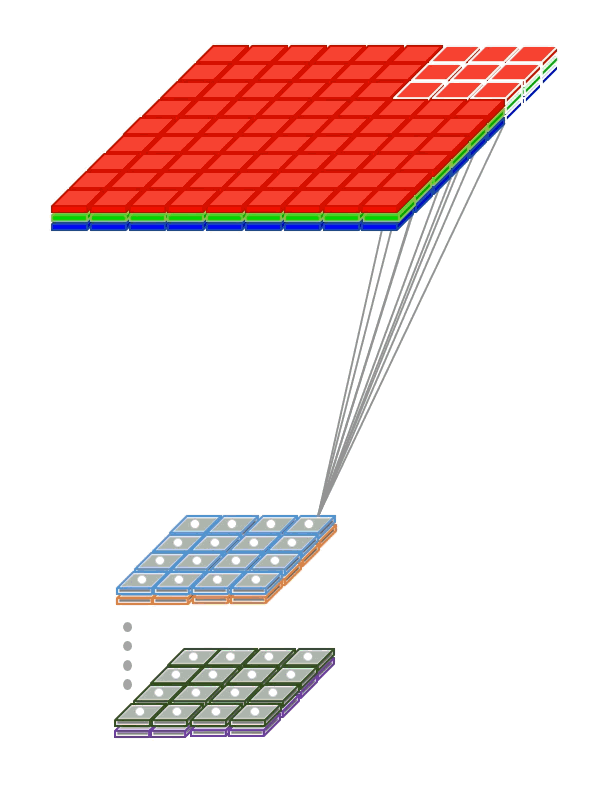
Для обработки изображений используется свертка, как и в обработке сигналов.
Опишем функцию свертки со следующими параметрами:
- kernel — ядро свёртки, матрица весов
- pad — сколько пискелей надо добавить к изображению по краям
- stride — частота применения фильтра. Например, для stride=2 будем брать каждый второй пиксель изображения по вертикали и горизонтали, уменьшив разрешение вдвое
In [1]:
def convolve(image, kernel, pad = 0, stride = 1):
rows, columns = image.shape
output_rows = rows // stride
output_columns = columns // stride
result = np.zeros((output_rows, output_columns))
if pad > 0:
image = np.pad(image, pad, 'constant')
kernel_size = kernel.size
kernel_length = kernel.shape[0]
half_kernel = kernel_length // 2
kernel_flat = kernel.reshape(kernel_size, 1)
offset = builtins.abs(half_kernel-pad)
for r in range(offset, rows - offset, stride):
for c in range(offset, columns - offset, stride):
rr = r - half_kernel + pad
cc = c - half_kernel + pad
patch = image[rr:rr + kernel_length, cc:cc + kernel_length]
result[r//stride,c//stride] = np.dot(patch.reshape(1, kernel_size), kernel_flat)
return result
In [2]:
def show_convolution(kernel, stride = 1):
"""Displays the effect of convolving with the given kernel."""
fig = pylab.figure(figsize = (9,9))
gs = gridspec.GridSpec(3, 3, height_ratios=[3,1,3])
start=1
for i in range(3):
image = images_train[start+i,0]
conv = convolve(image, kernel, kernel.shape[0]//2, stride)
ax = fig.add_subplot(gs[i])
pylab.imshow(image, interpolation='nearest')
ax.set_xticks([])
ax.set_yticks([])
ax = fig.add_subplot(gs[i + 3])
pylab.imshow(kernel, cmap='gray', interpolation='nearest')
ax.set_xticks([])
ax.set_yticks([])
ax = fig.add_subplot(gs[i + 6])
pylab.imshow(conv, interpolation='nearest')
ax.set_xticks([])
ax.set_yticks([])
pylab.show()
In [3]:
blur_kernel = np.array([[1, 4, 7, 4, 1],
[4, 16, 26, 16, 4],
[7, 26, 41, 26, 7],
[4, 16, 26, 16, 4],
[1, 4, 7, 4, 1]], dtype='float32')
blur_kernel /= 273
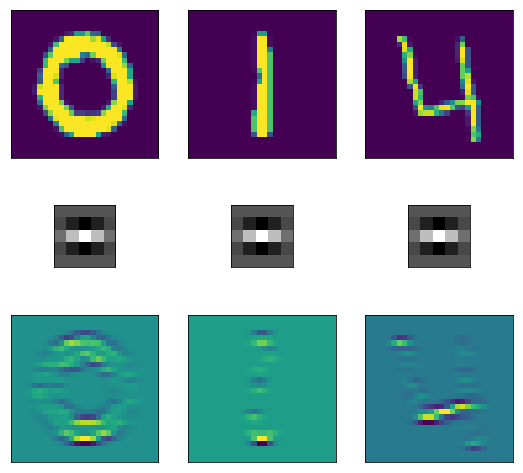
Фильтры
Blur
Фильтр размытия позволяет сгладить неровности и подчеркнуть общую форму объектов.

In [4]:
show_convolution(blur_kernel)
Вертикальные края
Можно придумать фильтр, выделяющий вертикальные переходы яркости на изображении. Здесь голубой цвет обозначает переход от чёрного к белому, желтый — наоборот.

In [5]:
vertical_edge_kernel = np.array([[1, 4, 0, -4, 1],
[4, 16, 0, -16, -4],
[7, 26, 0, -26, -7],
[4, 16, 0, -16, -4],
[1, 4, 0, -4, -1]], dtype='float32')
vertical_edge_kernel /= 166
In [6]:
show_convolution(vertical_edge_kernel)
Горизонтальные края
Аналогичный фильтр можно построить для выделения горизонтальных штрихов на изображении.
In [7]:
horizontal_bar_kernel = np.array([[0, 0, 0, 0, 0],
[-2, -8, -13, -8, -2],
[4, 16, 26, 16, 4],
[-2, -8, -13, -8, -2],
[0, 0, 0, 0, 0]], dtype='float32')
horizontal_bar_kernel /= 132
In [8]:
show_convolution(horizontal_bar_kernel)
Контурный фильтр
Также можно построить фильтр 9x9, который будет выделять контуры изображения.

In [9]:
blob_kernel = np.array([[0, 1, 1, 2, 2, 2, 1, 1, 0],
[1, 2, 4, 5, 5, 5, 4, 2, 1],
[1, 4, 5, 3, 0, 3, 5, 4, 1],
[2, 5, 3, -12, -24, -12, 3, 5, 2],
[2, 5, 0, -24, -40, -24, 0, 5, 2],
[2, 5, 3, -12, -24, -12, 3, 5, 2],
[1, 4, 5, 3, 0, 3, 5, 4, 1],
[1, 2, 4, 5, 5, 5, 4, 2, 1],
[0, 1, 1, 2, 2, 2, 1, 1, 0]], dtype='float32')
blob_kernel /= np.sum(np.abs(blob_kernel))
In [10]:
show_convolution(blob_kernel)
Таким образом работает классический пример с распознаванием цифр: у каждой цифры есть свои характерные геометрические черты (два круга — восьмерка, косая черта на половину изображения — единица и т.д.), по которым нейронная сеть может определить что за объект. Мы создаем фильтры, характеризующие каждую цифру, каждый из фильтров прогоняем по изображению и сводим ошибку к минимуму.
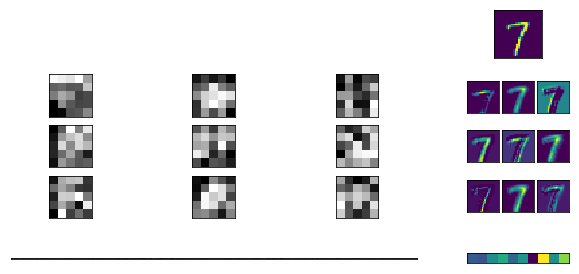
Если применить схожий подход к поиску котиков на картинке, быстро выяснится, что признаков у четвероногого для обучения нейросети масса, и все они разные: хвосты, уши, усы, носы, шерсть и окраска. И у каждого кота может быть ничего общего с другим. Нейросеть с небольшим количеством данных о структуре объекта не сможет понять, что один кот лежит, а второй стоит на задних лапах.
Основная идея свёрточной сети
- Создаем в нейросети свёрточный слой, который обеспечивает применение фильтра к изображению.
- Обучаем веса фильтра по алгоритму обратного распространения
К примеру, у нас есть изображение i, 2 сверточных фильтра w c выходами o. Элементы выходного изображения будут вычисляться следующим образом:
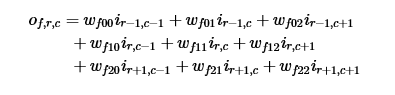
Тренировка весов
Алгоритм таков:
- Фильтр с одними и теми же весами применяется ко всем пикселям изображения.
- При этом фильтр «пробегает» по всему изображению.
- Мы хотим обучать эти веса (общие для всех пикселей) по алгоритму обратного распространения.
- Для этого надо свести применение фильтра к однократному умножению матриц.
- В отличие от полносвязного слоя, весов для обучения будет меньше, а примеров — больше.
- Хитрость — im2col
im2col
Начнем с изображения x, где каждый пиксель соответствует букве:
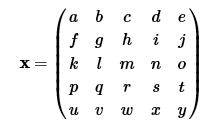
Затем мы извлечем все фрагменты изображения 3x3 и поместим их в столбцы большой матрицы X:

Теперь мы можем сохранить веса фильтров в обычной матрице, где каждая строка соответствует одному свёрточному фильтру:
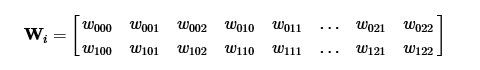
Тогда свёртка по всему изображению превращается в обычное матричное умножение:
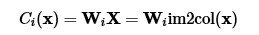
Проблемы анализа изображений
В процессе обучения может возникнуть множество подводных камней: некорректная выборка уже на втором слое загубит весь процесс обучения, она может быть недостаточно большой, из-за чего сеть не обучится выявлять всевозможные положения особенностей объекта.
Есть и обратная ситуация: при увеличении числа слоев происходит затухание градиента, появляется слишком большое число параметров, а функция может застрять в локальном минимуме.
В конце концов, кривой код тоже никто не отменял.
Чтобы научить работе с нейронными сетями, справляться с ее обучением и определять, где на практике можно воспользоваться машинным обучением, мы с Дмитрием Сошниковым разработали специальный курс Neuro Workshop. Конечно, на нем рассказывается и о том, как решать перечисленные выше проблемы.
Neuro Workshop пройдет 2 раза:
Выбирайте удобный день, приходите и задавайте Дмитрию свои вопросы.
Автор: De11