
Венгрия по праву может считаться математической сверхдержавой – и не только из-за «кубика Рубика», придуманного венгром Эрнё Рубиком. В 1894 году Венгрия первой в мире начала проводить математические олимпиады для подростков – за четыре десятилетия до того, как они стали проводиться где-то ещё. В том же году там начали издавать математический журнал KöMaL для учеников средней школы, в котором содержались различные задачки и приёмы для их решения. Олимпиада и журнал существуют до сих пор, с перерывами на мировые войны.
В результате венгры постоянно придумывают различные математические загадки, и в этой стране процент высококлассных математиков выше, чем в любой другой.
Директор американской математической олимпиады, венгр Бела Байнок, поделился с редакцией The Guardian «трёхмерными логическими загадками» — в таких задачках решение нужно искать при помощи трёхмерной решётки. Он сказал, что никогда не сталкивался с такими задачками за пределами Венгрии.
Вашему вниманию предлагается две созданные им задачки. Их можно решить при помощи расширенной двумерной решётки. Однако это правильнее будет сделать, нарисовав трёхмерную решётку – что-то вроде такой, какая получается на поверхности кубика Рубика.
1. Вечер свиданий
Андрей, Боря, Вася и Гриша пошли на свидания с Дашей, Еленой, Женей и Зиной. Об этих свиданиях мы знаем следующее:
- Андрей пойдёт в оперу.
- Боря проведёт вечер с Дашей.
- Вася не захочет пойти на свидание с Женей.
- Елена пойдёт в кино.
- Женя пойдёт на урок рукоделия.
Также известно, что одна парочка пойдёт на художественную выставку. Кто в итоге пойдёт с кем и куда?
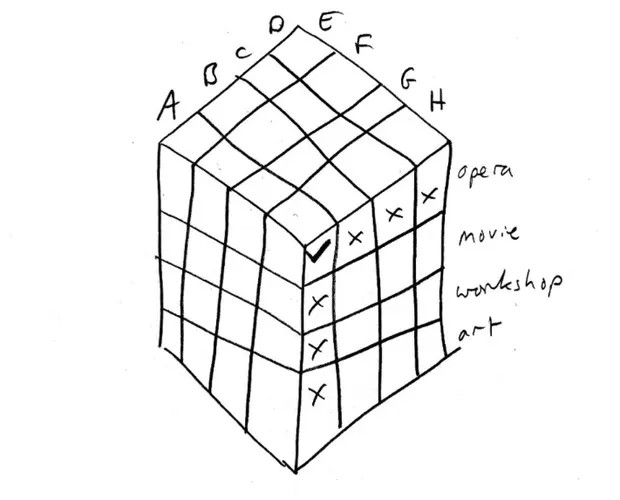
После этого нужно пройтись по всем утверждениям, и вносить в решётку информацию, где это возможно. Первое условие – Андрей пойдёт в оперу. Ставим галочку на пересечении Андрея и оперы, на правой грани куба. Предполагается, что каждое свидание пройдёт в одном месте, поэтому на остальных клетках напротив Андрея (кино, рукоделие и выставка) мы поставим крестики, поняв, что он туда не идёт. Соответственно, Боря, Вася и Гриша в оперу не пойдут, поэтому напротив них мы тоже ставим крестики.
Второе условие — Боря проведёт вечер с Дашей, поэтому на верхней грани появится галочка в клеточке на пересечении рядов для Бори и Даши. Продолжая таким образом, вы сможете заполнить всю решётку галочками и крестиками. На каждой из граней будет всего четыре галочки, и все они будут в разных строчках и столбцах. В итоге получится, что Андрей пойдёт в оперу с Зиной, Боря с Дашей пойдут на выставку, Василий с Еленой пойдут в кино, а Гриша с Женей отправятся на урок рукоделия.
2. Квартирная кража
Когда мистер Верона с женой открыли дверь своей квартиры в 11 утра сегодня, им глазам предстало ужасное зрелище: их прекрасную квартирку обокрали. Супруги вызвали полицию, приехавшую немедленно. Расследование принесло следующие результаты.
- В здании шесть квартир, с номерами от 1 до 6, чета Веронов живёт в квартире №4.
- Вероны ушли из дома вчера в 18 часов.
- Ночной охранник здания, мистер Сейф, работает с 18 до 10 утра.
- Ночью в здание входило шесть человек: Брим, Грин, Хилл, Смит, Тейлор и Уайт. Каждый из посетителей приходил в одну из квартир (каждый – в другую), и все они входили в здание в период от 18 до полуночи. Сейф не помнил, кто в какую квартиру приходил, но был уверен, что никто из них не гостил в доме больше часа. Более того, каждый из посетителей пришёл в свой час – первый с 18 до 19, второй с 19 до 20, и так далее.
- Брим был на большой вечеринке в загородном клубе, он прибыл туда в 20 часов, и оставался до полуночи.
- Грин тоже была в загородном клубе, она прибыла туда в 21 час, и уехала с Бримом.
- Хилл не смог обеспечить себя алиби за прошедшую ночь.
- Тейлор была дома, поливала дворик с 19:45 до 21 часа. Её видело несколько жильцов.
- Уайт был на вечеринке в загородном клубе. Он прибыл туда в 19 часов и уехал в 22 часа, однако в 23 часа вернулся и оставался далеко за полночь.
- Никто не мог войти в дом, не миновав лобби, в котором дежурил Сейф.
- В 5-й квартире не нашли отпечатков Смита, Тейлор или Уайта.
- Смит не мог посетить квартиры 1, 3 и 6.
- Грин не могла посетить квартиры 3 им 6.
- Сейф вспомнил, что незадолго до 20 часов посетитель ушёл из одной из квартир, то ли из №1, то ли из №4.
- До 19 часов никто не входил в квартиры 5 и 6.
- Гость прибыл в 20 часов, и пошёл в квартиру 1, 3 или 6.
- Никто не входил в квартиры 2 и 3 с 22 до 23 часов.
Это всё, что смогла установить полиция в первый день расследования. Можно ли распутать это ужасное преступление на основании только этих данных?
Автор: Вячеслав Голованов


