Неделю тридцатистрочников на JS стоит разбавить чем-нибудь действительно ненормальным.
Рекомендую перед прочтением ознакомиться, к примеру, с этим циклом статей или этой книгой; словарик языка здесь; тем не менее, я постараюсь подробно пояснять свои действия (все объяснения спрятаны под спойлеры, дабы не загромождать статью).
Если есть вопросы, предложения или исправления к коду — добро пожаловать в комментарии.
Готовим почву
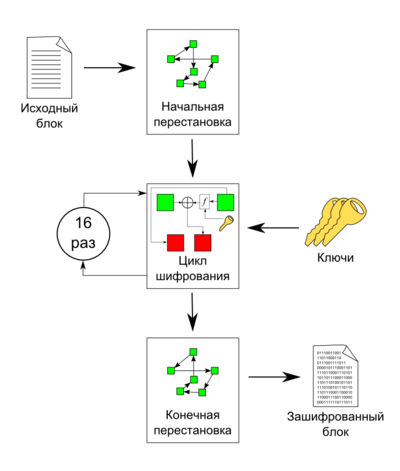
В DES используется несколько матриц, которые стоит подготовить загодя.
Матрица начальной перестановки P

Закономерность видна невооружённым взглядом: в верхней половине матрицы сверху вниз справа налево идут нечётные числа от 1 до 63, а каждый элемент нижней половины матрицы на единицу меньше соответствующего элемента верхней. Воспользуемся этим.
|: |. 8 4 $ >: +: i.32
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7
Код выполняется справа налево. По порядку:
i.32выдаёт 32 последовательных числа, начиная с нуля;+:удваивает свой операнд;>:увеличивает операнд на единицу;8 4 $преобразует операнд в матрицу 8x4;|.инвертирует главную ось матрицы, т.е. переставляет строки в обратном порядке;|:транспонирует матрицу.
i.32
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
+: i.32
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62
>: +: i.32
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63
8 4 $ >: +: i.32
1 3 5 7
9 11 13 15
17 19 21 23
25 27 29 31
33 35 37 39
41 43 45 47
49 51 53 55
57 59 61 63
|. 8 4 $ >: +: i.32
57 59 61 63
49 51 53 55
41 43 45 47
33 35 37 39
25 27 29 31
17 19 21 23
9 11 13 15
1 3 5 7
|: |. 8 4 $ >: +: i.32
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7
Получить нижнюю половину матрицы ничего не стоит:
<: |: |. 8 4 $ >: +: i.32
56 48 40 32 24 16 8 0
58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
Оператор <: уменьшает на единицу значение операнда.
Осталось это совместить — тут вступает в дело магия J:
(] , <:) |: |. 8 4 $ >: +: i.32
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 55 47 39 31 23 15 7
56 48 40 32 24 16 8 0
58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
Конструкция из трёх глаголов называется fork:
(f g h) y <-> (f y) g (h y)
Таким образом, конструкция выше эквивалентна этому:
(] |: |. 8 4 $ >: +: i.32) , (<: |: |. 8 4 $ >: +: i.32)
Диада , выполняет конкатенацию массивов, а ] просто возвращает свой правый операнд.
Монадный же вариант , «выпрямляет» матрицу в массив, что мы и используем, получая итоговую формулу для матрицы начальной перестановки:
P =: , (] , <:) |: |. 8 4 $ >: +: i.32
Матрица обратной перестановки P-1
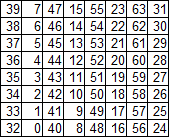
Эта матрица соотносится с P следующим образом: 0-й элемент P-1 равен 39, 39-й элемент P равен 0 и т.д.
Другими словами, элементы матрицы P-1 являются индексами своих индексов в матрице P. Звучит путано, но это лежит в основе формулы этой матрицы.
x (f g h) y <-> (x f y) g (x h y)
(i.64) ([ * =/~) P
Результат — матрица 64х64, где в каждой строке содержится её номер (скажем, i) в позиции P[i], а остальные элементы заполнены нулями.
Помимо fork'а используются наречия / и ~: первое применяет глагол к каждому элементу массива, а второе меняет операнды местами, так что
x f~ y <-> y f x
Если же мы напишем u/ y, где u — некоторый диадный глагол, J подставит его между всеми элементами y:
+/ 1 2 3 <-> 1 + 2 + 3
Или применим его к нашей матрице, сложив её строки и получив итоговую формулу:
iP =: +/ (i.64) ([ * =/~) P
Матрица начальной перестановки ключа G

Из ключа «выкидываются» 7-й, 15-й и так далее биты — они служат для контроля чётности.
Закономерность в G не так очевидна, тем не менее, матрицу G несложно получить из матрицы 8х8 последовательных чисел, из которой просто выкинули последний столбец.
}: |: i. 8 8
0 8 16 24 32 40 48 56
1 9 17 25 33 41 49 57
2 10 18 26 34 42 50 58
3 11 19 27 35 43 51 59
4 12 20 28 36 44 52 60
5 13 21 29 37 45 53 61
6 14 22 30 38 46 54 62
i. 8 8вместо массива чисел создаёт сразу матрицу 8х8 последовательных чисел.}:выкидывает последний элемент массива / строку матрицы.
Транспонирование — скорее побочный эффект, но именно в таком виде матрица нам и нужна.
Теперь нужно инвертировать строки — если просто применить к результату |., то поменяются местами строки целиком. В нашем же случае нужно изменить ранг глагола так, чтобы он работал с каждой отдельной строкой:
|."1 }: |: i. 8 8
56 48 40 32 24 16 8 0
57 49 41 33 25 17 9 1
58 50 42 34 26 18 10 2
59 51 43 35 27 19 11 3
60 52 44 36 28 20 12 4
61 53 45 37 29 21 13 5
62 54 46 38 30 22 14 6
" меняет ранг глагола. Ранг 0 означает, что глагол применяется к каждому элементу операнда, 1 — к строке и 2 — к матрице целиком.
Сохраним результат в переменную G — так будет удобнее.
Уже видно, что первые 28 элементов матрицы точно такие, как нам надо, ещё 24 можно получить, инвертировав порядок строк. Оставшиеся четыре элемента изящно вытащить у меня не получилось, так что просто впишем их как есть:
4 14 $ (28 {. , G), (24 {. , |. G), (27 19 11 3)
56 48 40 32 24 16 8 0 57 49 41 33 25 17
9 1 58 50 42 34 26 18 10 2 59 51 43 35
62 54 46 38 30 22 14 6 61 53 45 37 29 21
13 5 60 52 44 36 28 20 12 4 27 19 11 3
N {. y вытаскивает первые N элементов из y.
Сохраним результат.
G =: |."1 }: |: i. 8 8
G =: (28 {. , G), (24 {. , |. G), (27 19 11 3)
Матрица перестановки ключа KP
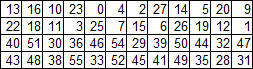
Тут всё печально — закономерности не видно, так что запишем матрицу, как есть.
Матрица сдвигов s
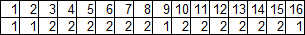
Первая строка — индексы, вторая — значения. Подробно останавливаться здесь не буду.
s =:1, (14 $ 1, 6 $ 2), 1
Матрица расширения E
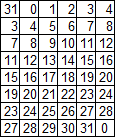
Эта матрица легко получается из i. 8 4: левый столбец циклически сдвигаем вниз и приставляем к матрице справа, правый — сдвигаем вверх и приставляем слева.
E =: |: i. 8 4
E =: , |: (_1 |. _1 { E) , E , (1 |. 0 { E)
Оператор x |. y выполняет циклический сдвиг массива.
Матрица перестановки P2 (да, в DES много перестановок)
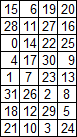
Здесь тоже не видно закономерностей. Поехали дальше.
Матрица преобразования S
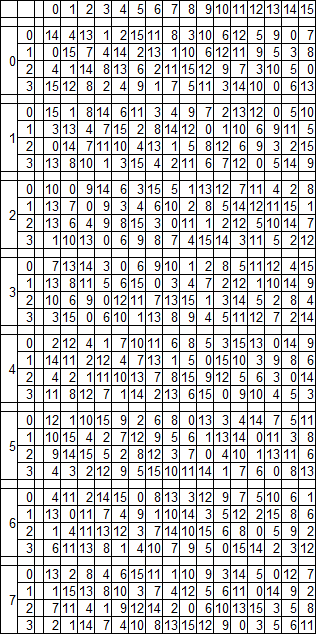
Она огромная, трёхмерная, и в ней тоже не видно совершенно никакой закономерности.
Матрицу эту мы запишем, как она есть, и заодно создадим пару глаголов, чтобы с ней потом было проще иметь дело.
f =: dyad : '|. #: S {~ < x, ((5{y)++:0{y), (+/(2^i.4)*}:}.y)' " 0 1
fS =: monad : '}. |."1 (4 $ 1), (i.8) f 8 6 $, y' " 2
i.8. Затем к результату добавляется строка из четырёх единиц, все строки матрицы инвертируются и первая строка удаляется.
Первый же глагол — диада с рангом 0 1 (такой ранг у диадного глагола означает, что к левому операнду применяется ранг 0, а к правому — 1). Этот глагол считает, что правый операнд — массив битов длины 6. 0-й и 5-й биты определяют номер строки в S, биты с 1-го по 4-й — номер столбца, а левый операнд — номер подматрицы. Все три полученных числа запихиваются в коробку (местный аналог структуры) и передаются на вход оператору { — взятие из массива по индексу. Оператор #: переводит результат в двоичную систему счисления, который следующим шагом инвертируется.
Вся эта эпопея с инвертированиями и добавлением-удалением строки из четырёх единиц нужна для добавления лидирующих нулей к строкам результата: если их не инвертировать изначально, нули добавляются в конце.
Переходим к делу
Сначала составляем список ключей, которые будем использовать (считаем, что key уже определён):
binkey =. chr2bin key
prmkey =. G { binkey
Затем возьмём первые 28 бит результата и составим список результатов сдвига:
C =. (28 {. prmkey) |.~"1 0 +/s
Из нового в этой строке только наречие : оно применяет глагол к каждому префиксу операнда.
s
1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
+/s
1 2 4 6 8 10 12 14 15 17 19 21 23 25 27 28
То же самое проделаем с последними 28 битами:
D =. (28 }. prmkey) |.~"1 0 +/s
N }. y отбрасывает первые N элементов y.
Теперь нам нужно выполнить конкатенацию соответствующих строк и применить к каждой строке результата матрицу перестановки ключа KP:
K =. KP {"1 C ," 1 1 D
binkey =. chr2bin key
prmkey =. G { binkey
C =. (28 {. prmkey) |.~"1 0 +/s
D =. (28 }. prmkey) |.~"1 0 +/s
K =. KP {"1 C ," 1 1 D
Исходный 8-байтный текст разбиваем на две 32-битные части:
bin =. chr2bin plain
prm =. P { bin
L =. 32 {. prm
R =. 32 }. prm
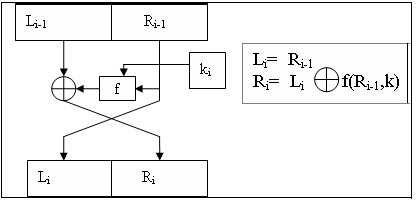
Теперь нам нужно каждый из ключей применить к паре L, R следующим образом:
Для этого создадим рекурсивную монаду, которая принимает на вход коробку с тремя значениями и возвращает похожую коробку.
> «открывает» коробку, возвращая её содержимое.
K =. > 0 { y
L =. > 1 { y
R =. > 2 { y
Функция f на картинке выше делает следующее:
- применяет матрицу расширения Е к R;
- складывает результат с ключом по модулю 2;
- для каждого шестибитного блока результата находит соответствующее четырёхбитное число в матрице S;
- применяет к этому матрицу перестановки P2;
- складывает результат с L по модулю 2;
Как удачно, что для пункта 3 у нас есть специальный глагол! Всё предыдущее описывается простой строчкой:
L ~: P2 { , fS (0 { K) ~: E { R
step =: monad define
K =. > 0 { y
L =. > 1 { y
R =. > 2 { y
(}. K); R ; L ~: P2 { , fS (0 { K) ~: E { R
)
И вызовем её столько раз, сколько ключей у нас есть:
result =. step^:(#K) K; L; R
u^:N, который выполняет глагол u N раз, то есть, например,u^:4 y <-> u u u u yСнова поменяем местами L и R и получим зашифрованный текст.
R =. > 1 { result
L =. > 2 { result
bin2chr iP { ,L,R
Обернём всё получившееся в диаду, которая принимает левым операндом ключ, а правым — 8-байтный массив:
encode =: dyad define
key =. x
binkey =. chr2bin key
prmkey =. G { binkey
C =. (28 {. prmkey) |.~"1 0 +/s
D =. (28 }. prmkey) |.~"1 0 +/s
K =. KP {"1 C ," 1 1 D
plain =. y
bin =. chr2bin plain
prm =. P { bin
L =. 32 {. prm
R =. 32 }. prm
result =. step^:(#K) K; L; R
R =. > 1 { result
L =. > 2 { result
bin2chr iP { ,L,R
)
Расшифровка выполняется точно так же, с той лишь разницей, что ключи применяются в обратном порядке.
Перед применением того, что у нас получилось, нужно подготовить текст:
in.txt:
Lorem ipsum dolor sit amet consectetur adipiscing elit.
1!:1 считывает содержимое файла
plaintext =: 1!:1 < 'in.txt'
Поскольку алгоритм работает с блоками по 8 символов, лучше забить хвост пробелами, иначе текст просто будет повторяться:
' ',~^:(8 - 8| # plaintext) plaintext
А теперь разобьём текст на блоки по 8 символов.
plaintext =: (8,~ >. 8 %~ #plaintext) $, ' ',~^:(8 - 8| # plaintext) plaintext
plaintext =: 1!:1 < 'in.txt'
plaintext =: (8,~ >. 8 %~ #plaintext) $, ' ',~^:(8 - 8| # plaintext) plaintext
Запишем результат в файл.
1!:21 открывает файл, 1!:22 — закрывает, а 1!:2 пишет в файлout =: 1!:21 < 'out.txt'
('habrhabr' encode"1 1 plaintext) 1!:2 out
1!:22 out
out.txt:
4acc c8ad 32dd 96a1 ae9c 2fdc 2025 e3d0 968c 97c0 5544 0944 2d20 2069 f943 f0d4 e98d bdea 71f9 c516 8a0a b034 5641 b0b5 53cc 2355 2fb1 4bde
И попробуем расшифровать результат.
cipher =: 1!:1 < 'out.txt'
cipher =: (8,~ >. 8 %~ #cipher) $, cipher
, 'habrhabr' decode"1 1 cipher
Lorem ipsum dolor sit amet consectetur adipiscing elit.
Код целиком на пейстбине.
Если есть вопросы, предложения или исправления к коду — добро пожаловать в комментарии.
Всем спасибо за внимание!
Автор: AraneusAdoro