Безотказный способ вовлечь людей в дискуссию — регулярно публиковать эту штуку в Twitter. Иногда я ненавижу подобные скрупулёзные разборы тем, но в данном случае, к чёрту, давайте разберём эту хреновину по косточкам, и посмотрим, сколько полезной информации мы можем из неё извлечь.
Начнём с очевидного.
-
Ожидаемая стоимость при выборе зелёной кнопки цвета составляет $25 млн.
-
Многие люди выберут красный. Некоторые из этих людей знают, что ожидаемая стоимость зелёного цвета составляет $25 млн, и всё равно выбирают красный.
Здесь нет никакого диссонанса. Красная кнопка гарантирует совершенно новую жизнь большей части населения планеты. Зелёная кнопка означает, им всё равно, возможно, придётся заводить будильник на завтра и вставать на работу.
Радость от богатства работает по принципу убывающей отдачи. Я только что нашёл 40 долларов в паре штанов, которые давно не носил (и ещё ковидную маску). Если бы такое случилось 25 лет назад, это было бы достаточно серьёзной находкой, чтобы я побежал в местное отделение банка, открывать накопительный счёт.
Экономисты говорят о «выгодности» богатства. Они демонстрируют эту концепцию с помощью сублинейной функции, связывающей «полезность» с количеством богатства. Обычно это логарифмическая или степенная функция. Сублинейная она потому, что «если ваше богатство удвоится, ваше счастье увеличится, но не в 2 раза». А об эмпирической форме этой функции учёные долго будут спорить.
Мы будем говорить, что ваши «полезности», выдуманные единицы удовлетворения, равны кубическому корню из богатства:
Начнём с самого простого графика.
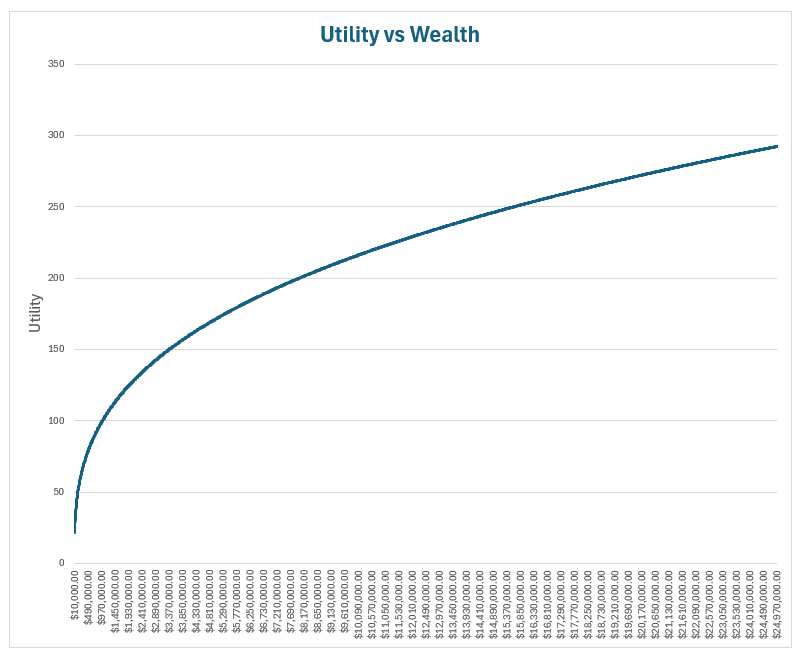
-
При увеличении вашего благосостояния в 100 раз с $10 тыс. до $1 млн эта функция говорит, что вы становитесь счастливее примерно в 5 раз.
-
При увеличении вашего состояния в 2 500 раз с $10 тыс. до $25 млн эта функция говорит, что вы становитесь счастливее «всего» в 13 раз.
Функция разумна — счастье растёт медленнее, но при этом утверждает, что большее богатство всегда лучше меньшего (это я бы назвал «условием отсутствия арбитража» — если бы это было не так, вы могли бы просто раздавать деньги).
Но точно так же, как вы хотите рассматривать долгосрочные доходы от инвестирования на логарифмическом графике (компаундинг — это экспоненциальная функция), мы хотим сжать график, чтобы получить более масштабный вид. К тому же, среди читателей есть немалое количество людей с состоянием более $25 млн, а мы хотим охватить всю аудиторию, верно?
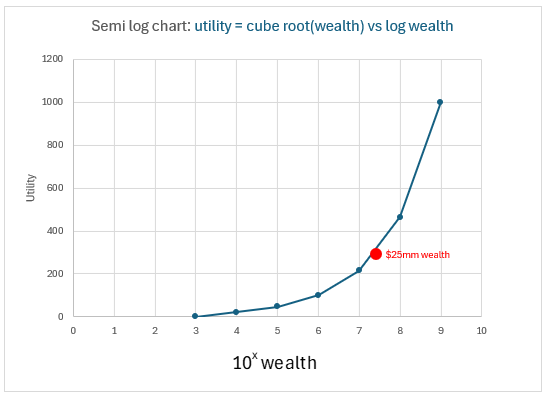
Давайте преобразуем ось богатства в ось log(wealth), используя 10 x (т. е. $1 000 = 103).
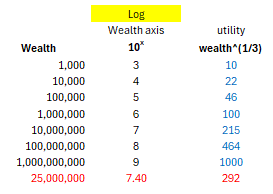
Таблица, лежащая в его основе:
Мы используем логарифмические диаграммы для более функционального представления информации.
Используя log (base-10) для преобразования оси богатства, мы теперь можем увидеть, что означает кубический корень полезности:
На каждом порядке увеличения богатства ваше счастье удваивается.
Если ваше богатство увеличится в 10 раз, ваше счастье возрастёт примерно в 2 раза.
Но тут есть ещё один забавный момент.
Когда я смотрю на этот полулогарифмический график, меня беспокоит, что он всё ещё экспоненциальный. Полезность растёт в 2 раза.
В случае с экспоненциальными функциями (например, с суммированными доходами в контексте инвестирования) полулогарифмическая диаграмма создаёт прямую линию.
Но функция кубического корня — это степенная функция. Чтобы получить прямую линию, мы должны использовать логарифмический график вместо полулогарифмического!
Давайте сделаем это и посмотрим, почему такое преобразование помогает в интерпретации. Сначала таблица:
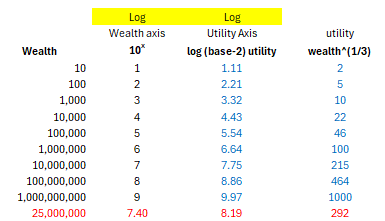
Удобно использовать log (base-2) для оси полезности, потому что полезность растёт в 2 раза.
А вот логарифмическая диаграмма:
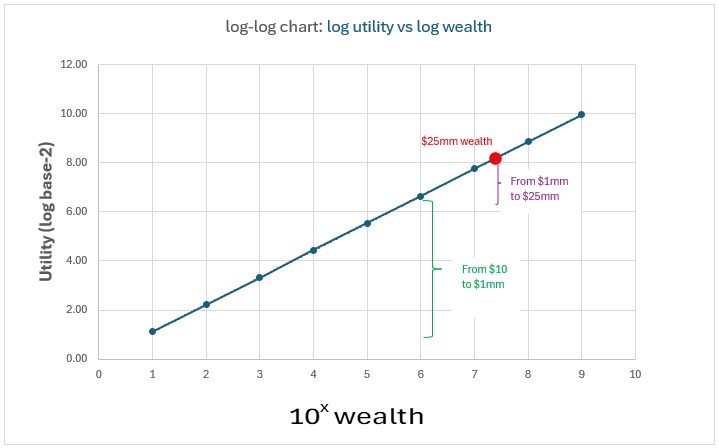
Наблюдения:
-
Ось x — log base-10 (богатство), а ось y — log base-2 (полезность), и мы получаем прямую линию — это позволяет сделать простой вывод: Каждый порядок увеличения богатства удваивает наше счастье.
-
Очевидно, почему многие предпочтут гарантию в $1 млн ожидаемой стоимости в $25 млн — если у вас есть $10 сегодня, ваше счастье удваивается более чем в 6 раз (оно увеличивается более чем в 50 раз, от 2 до 100) на протяжении 5 порядков величины. Счастье увеличивается только примерно в 3 раза (от 100 до 292) между $1 млн и $25 млн. Эти $24 млн «стоят» меньше, чем самый первый $1 млн.
Конечно, эта функция полезности необязательно описывает какого-либо человека, но качественно выводится из идеи, что ваш образ жизни выглядит довольно похожим, пока вы не подниметесь на более высокий порядок богатства. Мы можем спорить о фактической скорости, но если вы не страдаете манией величия, она почти наверняка будет сублинейной.
В следующий раз, когда вы увидите вопрос о красной/зелёной кнопке, вы сможете оценить, насколько рациональными являются ответы людей, несмотря на все их заблуждения по поводу увеличения математического ожидания.
Дополнение
В этом обзоре было показано, как выбрать преобразования логарифмов для преобразования экспоненциальных графиков в линейные и сохранить интуицию, говоря такие вещи, как
-
«Y увеличивается на фиксированную величину при увеличении X на порядок (log base-10)»
-
«Y увеличивается на фиксированную величину каждый раз, когда X удваивается (log base-2)».
Вывод линейных преобразований полулогарифмической и логарифмической линейки:
-
Почему экспоненциальные функции линейны на полулогарифмических графиках?
Начните с логарифмирования обеих сторон экспоненциальной функции:
Y = a<sup>X</sup>
Log(Y) = X log(a)
что выглядит как линия: Y = mX + b
где:
X log(a) соответствует mX, поэтому наклон или m= log(a)
-
Степенные функции линейны на логарифмических графиках.
Вывод путём взятия логарифма обеих сторон силовой функции:
Y = aXb
log(Y) = log(aXb)
log(Y) = log(a) + log(Xb)
log(Y) = b log(X) + log(a)
что выглядит как линия: Y = mX + b
где пересечение - log(a), а наклон – экспонента от b.
Взгляд с точки зрения денег
Если в вас течёт кровь трейдера, вы посмотрите на вопрос выше и скажете: «Я просто продам этот красно-зелёный опцион на аукционе тому, кто больше заплатит».
Как вы думаете, какую цену вы получите?
Давайте порассуждаем.
Тот, кого не беспокоит риск, одинаково оценит гарантированный $1 млн и ожидаемый $1 млн.
Красная кнопка даёт $25 млн, поэтому наш нейтральный к риску друг Спок не заплатит больше $24 млн за возможность нажать на неё.
Доказательство того, что $1 млн останется в ожидании, если вы заплатите $24 млн:
.50 * -$24 млн + .50 * $26 млн = $1 млн.
К сожалению, всё, что мы пока сделали, — это определили верхнюю границу в $24 млн, которые можно заплатить за этот вариант.
Но как вы думаете, сколько на самом деле кто-то заплатит?
Давайте сделаем это более понятным и посмотрим, сможем ли мы вывести нашу логику на новый уровень.
Представьте, что зелёная кнопка гарантирует всего 1 доллар, а красная — 50 % шансов на 50 долларов.
Заплатили бы вы 24 доллара? Вероятно, нет, если только вы не любите риски, но это не исключено. Ведь у [торгового приложения] Robinhood миллионы пользователей, которые торгуют ради удовольствия, а дети из рекламы E-trade снова появились в рекламе Super Bowl.
Заплатили бы вы $23, чтобы нажать на красную кнопку? $22? Если вы не хотите платить $20, пожалуйста, закройте эту вкладку прямо сейчас.
Этим мысленным экспериментом я добиваюсь того, чтобы вы почувствовали, что ответ на вопрос зависит от:
-
ваших финансовых ресурсов (поставить на кон 20 долларов вполне можно и приемлемо, играть на все деньги, что у вас есть — не очень)
-
ваших предпочтений в отношении риска.
С учётом этого мы можем перейти к следующему разделу, где мы сгенерируем конкретный ответ на первоначальный вопрос.
Взгляд с точки зрения денег для мазохистов
24 миллиона долларов для человека с состоянием в 100 миллиардов долларов — это то же самое, что 24 доллара для человека с состоянием в 100 тысяч долларов.
В мире найдётся 10 человек, которые могут бесстрастно принять эту ставку так же легко, как кто-то просто сыграет в азартную игру с $20.
Но, как и в случае с поиском верхней границы того, что кто-то может заплатить, это лишь начало.
Это отличное место для использования критерия Келли. Вкратце, критерий Келли — это формула, которая предписывает идеальный процент от вашего капитала для ставок. Предписанная доля — это математическое решение вопроса «На какую сумму я должен поставить, чтобы максимизировать темпы роста?»
Я создал подборку статей для тех, кто хочет узнать больше (предостережения, история и многое другое). Но сейчас мы хотим сосредоточиться на нашем вопросе.
Формула Келли для определения доли вашего богатства, на которую следует делать ставки, проста:
f* = Edge / Odds
где
f* = доля богатства
Edge = ожидаемая прибыль
Odds = процент прибыли при выигрыше
Если мои первоначальные инвестиции составляют $24 млн, и я ожидаю заработать $1 млн, то:
Edge = 24 млн = 4.17%.
Когда я выигрываю, я зарабатываю $26 млн для ставки в $24 млн:
Odds = 26/24 = 108,33%.
f* = edge/odds = 4,17% / 108,33% = 3,85%
Келли советует ставить на это предложение 3,85% вашего капитала.
$24 млн — это 3,85% от базовой стоимости в $624 млн.
Число фондов, торговых фирм или даже частных лиц, которые могут обоснованно принять эту ставку, намного больше, чем 10 самых богатых людей.
И помните, что эта ставка представляет собой простую игру — она не связана с рынками или экономическим ростом. Торговые фирмы постоянно диверсифицируют подобные ставки. Как человек, торгующий на бирже, я бы описал этот бизнес как «заплатите мне 10 000 долларов вперёд, и я подброшу с вами монету стоимостью 1 миллион долларов».
Если монета честная, то она стоит $500 тысяч, и я, по сути, покупаю её за $490 тысяч или продаю за $510 тысяч. В любом случае я получу 2% с прибыли.
Мои шансы составляют 490k = 104,08%.
Рекомендованный размер ставки составляет 2%/104,08% = 1,9%, что лишь наполовину лучше, чем красная кнопка за $24 млн! [Маркет-мейкинг в одном предложении: Делать десятицентовые преимущества на опционе за $5 несколько десятков раз в день, убеждаться, что преимущества реальны, и управлять рисками].
Так что да, я ожидаю, что возможность нажать на красную кнопку будет продавать примерно за $24 млн какая-нибудь крупная фирма, привыкшая брать на себя риски за определённую плату.
Автор: Вячеслав Голованов






