В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств.
Содержание
I. Пересечение упорядоченных множеств
II. Разность упорядоченных множеств
III. Объединение упорядоченных множеств
IV. Симметрическая разность упорядоченных множеств
Заключение
I. Пересечение упорядоченных множеств
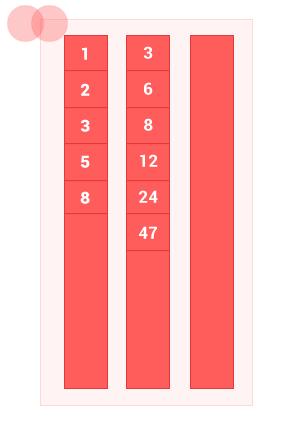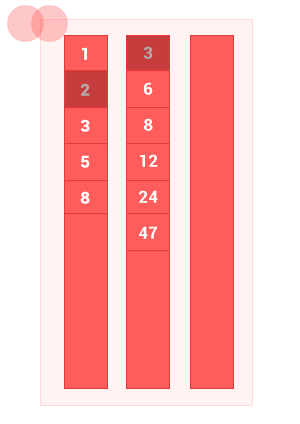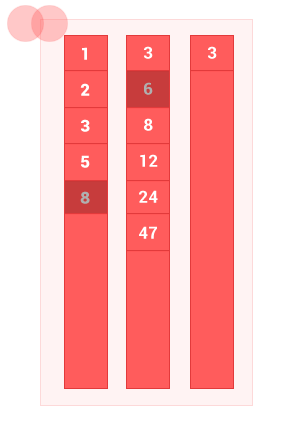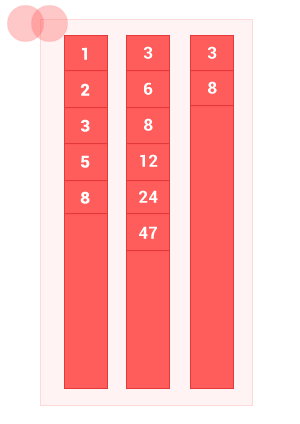
Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.
Сделал небольшую анимацию, чтобы показать как работает алгоритм.
Пример реализации на javascript:
function intersec_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
array_3[k] = array_1[i]; // запишем элемент в массив array_3
k++,i++,j++; // и сдвинем позицию во всех 3 массивах
} else {
if (array_1[i] < array_2[j]) {
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
return array_3;
}
Обращение к функции:
intersec_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [3, 8]
II. Разность упорядоченных множеств
Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
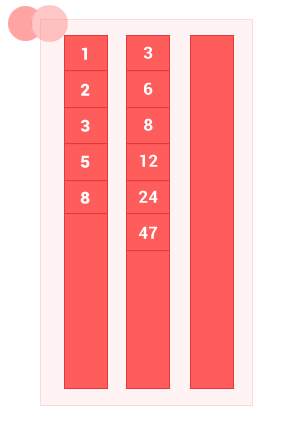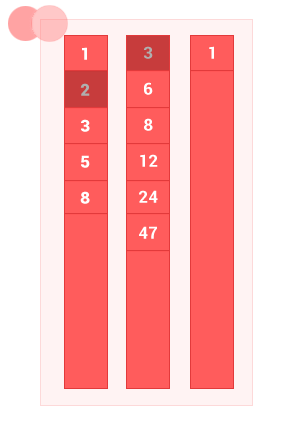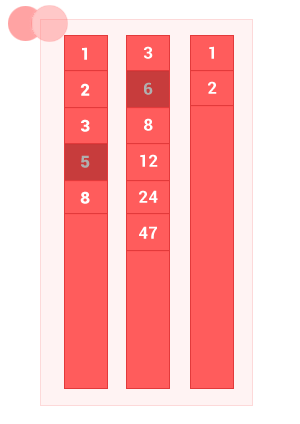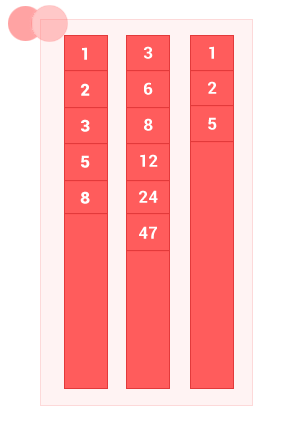
function diff_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
i++,j++;
} else {
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
if (i < n)
{
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
}
return array_3;
}
diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 5]
III. Объединение упорядоченных множеств
Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
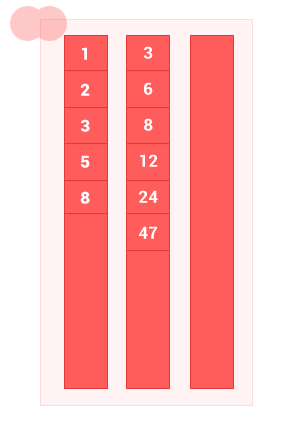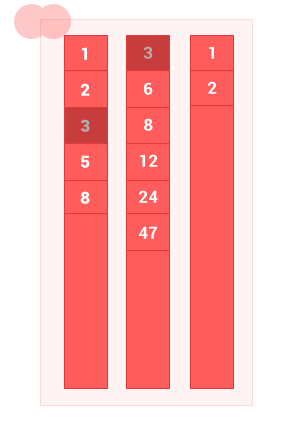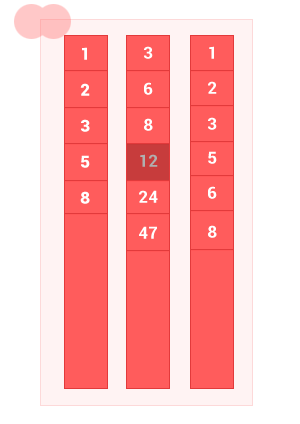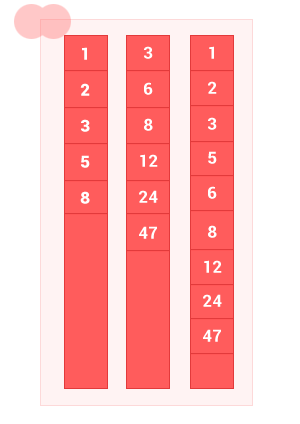
function sum_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
array_3[k] = array_1[i];
k++,i++,j++;
} else {
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
array_3[k] = array_2[j];
k++;
j++; // сдвинем позицию во втором массиве
}
}
}
if (i < n)
{
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
} else {
if (j < m)
{
while (j < m) {
array_3[k] = array_2[j];
k++, j++;
}
}
}
return array_3;
}
sum_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 3, 5, 6, 8, 12, 24, 47]
IV. Симметрическая разность упорядоченных множеств
Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.
По сути это вычитание множеств, сначала A из B, затем B из A.
function symmetric_diff_sort_arr(array_1,array_2)
{
var n = array_1.length, m = array_2.length, i = 0, k = 0, j = 0, array_3 = [];
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_1[i] == array_2[j])
{
i++,j++;
} else {
if (array_1[i] < array_2[j]) {
array_3[k] = array_1[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
if (i < n)
{
while (i < n) {
array_3[k] = array_1[i];
k++, i++;
}
}
n = array_2.length, m = array_1.length, j = 0, i = 0;
while ((i < n) && (j < m)) // пока не дошли до конца массива
{
if (array_2[i] == array_1[j])
{
i++,j++;
} else {
if (array_2[i] < array_1[j]) {
array_3[k] = array_2[i];
k++;
i++; // сдвинем позицию в первом массиве
} else {
j++; // сдвинем позицию во втором массиве
}
}
}
if (i < n)
{
while (i < n) {
array_3[k] = array_2[i];
k++, i++;
}
}
return array_3;
}
symmetric_diff_sort_arr([1, 2, 3, 5, 8], [3, 6, 8, 12, 24, 47]); // на выходе [1, 2, 5, 6, 12, 24, 47]
Заключение
Мне часто приходится работать с отсортированными массивами, поэтому эти алгоритмы очень сильно ускоряют процесс. Пример реализации метода intersec_sort_arr, вы можете посмотреть в моем приложении для vk.com. С помощью данного метода я нахожу общих участников сообществ работая с отсортированными массивами, в миллионы элементов, метод справляется очень быстро. До этого использовал метод описанный в моей предыдущей статье, обработка массивов была очень медленной.
Автор: dooza




