Здравствуйте!
На сегодняшний день в веб-проектировании такое понятие, как Usability, является главенствующим. Существует множество подходов увеличения эффективности взаимодействия пользователя с меню. В этой публикации я приведу пример работы с паркетным меню, но в более упрощенном стиле, не похожем на меню Windows 8.
Для начала приведем формулировку закона Фиттса:
— общий закон, касающийся сенсорно-моторных процессов, связывающий время движения с точностью движения и с расстоянием перемещения: чем дальше или точнее выполняется движение, тем больше коррекции необходимо для его выполнения, и соответственно, больше времени требуется для внесения этой коррекции.
Формула:
T = a + b * log ( D / W + 1 ),
где T — время работы пользователя с меню в (мс), a и b — коэффициенты навыков и умений работы пользователя с тем или иным устройством, D — расстояние от одного до другого пункта меню, W — ширина пункта меню при движении к нему от другого пункта меню.
Для большего понимания представим расчетную схему:
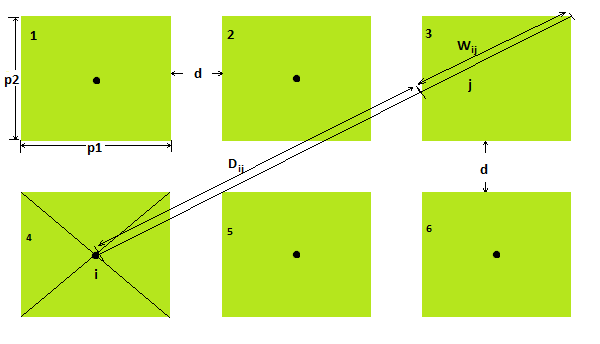
Рисунок — Расчетная схема закона Фиттса.
Для достижения нужных результатов я провел несколько опытов на написанной мной программе. На данный момент программа может проанализировать заданное вами меню и выдать результаты для нескольких пользователей с учетом их умений и навыков работы с компьютером.
Рассчитаем среднее время для паркетного меню с параметрами: p1=120 px, p2=160 px, d=10 px, n=6, где n – количество пунктов меню.
Получим таблицу, в которой указаны параметры Wi, Di, Ti.
| i | Wi | Di | Ti |
| 1 | 143.323 | 193.484 | 329.433 |
| 2 | 131.39 | 152.678 | 316.512 |
| 3 | 143.323 | 193.484 | 329.433 |
| 4 | 143.323 | 193.484 | 329.433 |
| 5 | 131.39 | 152.678 | 316.512 |
| 6 | 143.323 | 193.484 | 329.433 |
| Среднее значение | 115.458 | 147.634 | 324.657 |
Результаты таблицы показывают, что для повышения эффективности взаимодействия пользователя с паркетным меню наиболее часто выбираемые элементы должны быть расположены под №2 и №4.
В качестве практического примера рассмотрим такую задачу: необходимо построить паркетное меню, которое будет состоять из 6-ти элементов с определенными наименованиями, а именно — Моя страница, Мои партнеры, Мои заказы, Сообщения, Мои компании, Люди. Приведем таблицу вероятности выбора каждого пункта меню.
| 1. Моя страницы | 0.25 |
| 2. Мои партнеры | 0.17 |
| 3. Мои заказы | 0.15 |
| 4. Сообщения | 0.13 |
| 5. Мои компании | 0.1 |
| 6. Люди | 0.2 |
В данном примере условием для расчета является не равновероятный выбор произвольного пункта меню, таким образом, расчет D и W будет изменен с учетом вероятности.
Расположим пункты меню в двух вариантах последовательно, как показано на расчетной схеме:
Первый вариант: Моя страница -> Сообщения -> Мои заказы -> Люди -> Мои компании -> Мои партнеры
Второй вариант: Сообщения -> Моя страница -> Мои заказы -> Мои компании -> Люди -> Мои партнеры
Результаты для первого варианта: D = 184.098 px, W = 140.578 px, T = 326.744 мс
Результаты для второго варианта: D = 175.121 px, W = 137.953 px, T = 324.026 мс
Из полученных данных можно сделать вывод, что второй вариант расположения пунктов меню является более эффективным по сравнению с первым.
В заключение хотелось бы добавить, что на данный момент программа считает только сухие теоретические цифры. В дальнейшем будет расчет не только для паркетного, но и для более сложных меню. Так же будет создана система для реальных пользователей с учетом вероятности выбора, чтобы в дальнейшем получить реальные данные сравнить с теоретическими и возможно получить некий коэффициент поправки.
Спасибо за внимание!
P.S. — К большому сожалению, я не смог вам полностью описать все формулы, это связано с тем, что я пока не до конца разобрался в постинге на хабре, но хочу сказать, что буду рад, если мои данные или наблюдения помогут в работе или написании более лучшего и эффективного меню, чем есть сейчас.
Список литературы
1. Статья Википедии / Usability / goo.gl/DJM3OP
2. Статья Википедии / Закон Фиттса / goo.gl/worZ3z
3. Губко М.В., Даниленко А.И Математическая модель оптимизации структуры иерархического меню // Проблемы управления. — 2010. — №4. — С.49-58.
Автор: swpo






