Руководство хакера по нейронным сетям. Схемы реальных значений. Шаблоны в «обратном» потоке. Пример «Один нейрон»

   Введение
   Глава 1: Схемы реальных значений
      Базовый сценарий: Простой логический элемент в схеме
      Цель
         Стратегия №1: Произвольный локальный поиск

         Стратегия №2: Числовой градиент

         Стратегия №3: Аналитический градиент

      Схемы с несколькими логическими элементами
         Обратное распространение ошибки

         Шаблоны в «обратном» потоке 
      Пример "Один нейрон"

Давайте снова посмотрим на наш пример схемы с введенными числами. Первая схема показывает нам «сырые» значения, а вторая – градиенты, которые возвращаются к исходным значениям, как обсуждалось ранее. Обратите внимание, что градиент всегда сводится к +1. Это стандартный толчок для схемы, в которой должно увеличиться значение.

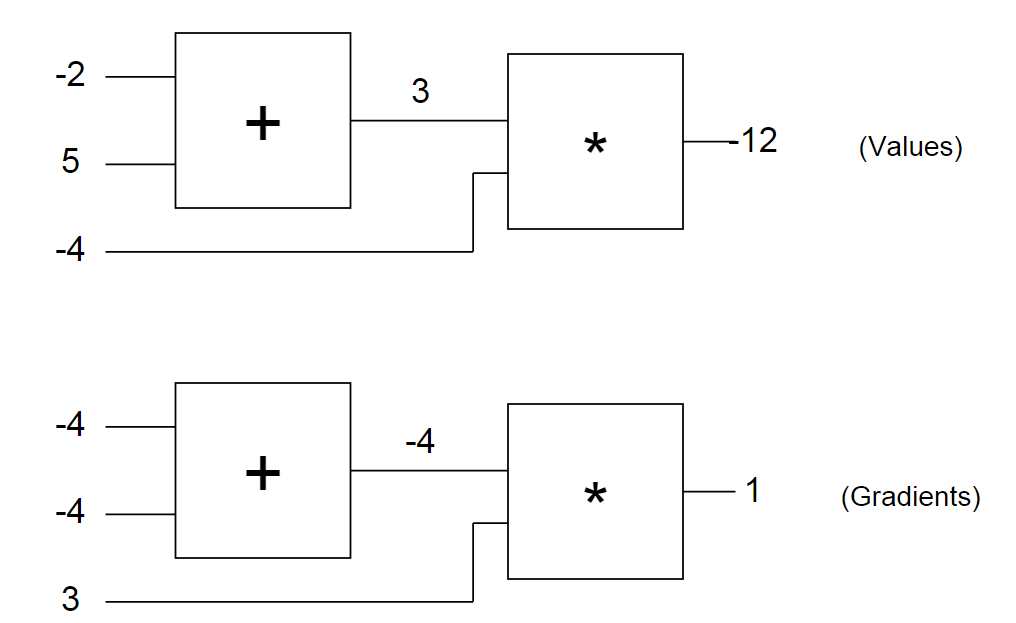
Через какое-то время вы начнете замечать шаблоны в том, как градиенты возвращаются по схеме. Например, логический элемент + всегда поднимает градиент и просто передает его на все исходные значения (обратите внимание, в примере с -4 он был просто передан на оба исходных значения логического элемента +). Это потому, что его собственная производная для исходных значений равна +1, вне зависимости от того, чему равны фактические значения исходных данных, поэтому в цепном правиле градиент сверху просто умножается на 1 и остается таким же.

Тоже самое происходит, например, с логическим элементом max(x,y). Так как градиент элемента max(x,y) по отношению к своим исходным значениям равен +1 для того значения x или y, которое больше, и 0 для второго, этот логический элемент в процессе обратного распределения ошибки эффективно используется только в качестве «переключателя» градиента: он берет градиент сверху и «направляет» его к исходному значению, которое оказывается выше при обратном проходе.

Проверка числового градиента

Прежде чем мы закончим с этим разделом, давайте просто убедимся, что аналитический градиент, который мы вычислили для обратного распространения ошибки, правильный. Давайте вспомним, что мы можем сделать это, просто рассчитав числовой градиент, и убедившись, что получим [-4, -4, 3] для x,y,z. Вот код:

// стартовые условия
var x = -2, y = 5, z = -4;

// проверка числового градиента
var h = 0.0001;
var x_derivative = (forwardCircuit(x+h,y,z) - forwardCircuit(x,y,z)) / h; // -4
var y_derivative = (forwardCircuit(x,y+h,z) - forwardCircuit(x,y,z)) / h; // -4
var z_derivative = (forwardCircuit(x,y,z+h) - forwardCircuit(x,y,z)) / h; // 3

Пример: Один нейрон

В предыдущем разделе вы, наконец, разобрались с понятием обратного распространения ошибки. Давайте теперь рассмотрим более сложный и практический пример. Мы рассмотрим двухмерный нейрон, который вычисляет следующую функцию:

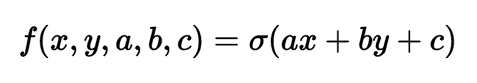
В этом выражении σ представляет собой сигмоидную функцию. Ее можно описать как «сжимающую функцию», так как она берет исходное значение и сжимает его, чтобы оно оказалось между нулем и единицей: Крайне отрицательные значения сжимаются в сторону нуля, а положительные значения сжимаются в сторону единицы. Например, у нас есть выражение sig(-5) = 0.006, sig(0) = 0.5, sig(5) = 0.993. Сигмоидная функция определяется следующим образом:

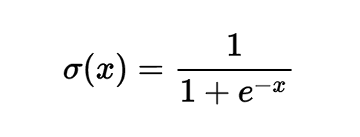
Градиент по отношению к его единственному исходному значению, как указано в Википедии (или, если вы разбираетесь в методах расчета, можете вычислить его самостоятельно), имеет вид следующего выражения:

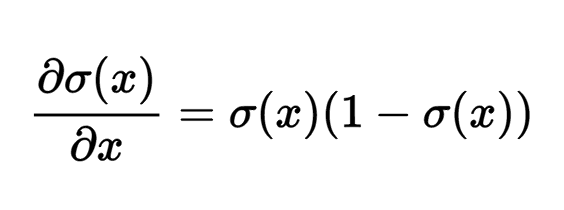
Например, если исходным значением сигмоидного логического элемента является x = 3, логический элемент будет вычислять результат уравнения f = 1.0 / (1.0 + Math.exp(-x)) = 0.95, после чего (локальный) градиент по его исходному значению будет иметь следующий вид: dx = (0.95) * (1 — 0.95) = 0.0475.

Это все, что нам нужно, чтобы использовать этот логический элемент: мы знаем, как взять исходное значение и продвинуть его через сигмоидный логический элемент, а также у нас есть выражение для градиента по отношению к его исходному значению, поэтому мы можем также выполнить обратное распределение ошибки с его помощью. Еще один момент, на который стоит обратить внимание – технически сигмоидная функция состоит из целого набора логических элементов, расположенных в ряд, которые вычисляют дополнительные атомические функции: логический элемент возведения в степень, прибавления и деления. Такое отношение работает отлично, но для этого примера я решил сжать все эти логические элементы до одного, который вычисляет сигмоиду за один раз, так как выражение градиента оказалось довольно простым.

Давайте воспользуемся этой возможностью тщательно структурировать связанный код удобным модульным способом. Для начала я бы хотел обратить ваше внимание, что каждая линия в наших графиках имеет две связанные с ней цифры:

1. Значение, которое она имеет при прямом проходе
2. Градиент (т.е. толчок), который проходит обратно по ней при обратном проходе

Давайте создадим простую структуру сегмента (Unit), которая будет сохранять эти два значения по каждой линии. Наши логические элементы не будут работать поверх сегментов: они будут принимать их в качестве исходных значений и создавать их в виде выходных значений.

// каждый сегмент отвечает линии на графиках
var Unit = function(value, grad) {
  // значение, рассчитанное при переднем проходе
  this.value = value; 
  // производная результата схемы по отношению к этому сегменту, рассчитанная при обратном проходе
  this.grad = grad; 
}

Кроме сегментов, нам также нужны три логических элемента: +, * и sig (сигмоида). Давайте начнем с применения логического элемента умножения. Здесь я использую Javascript, который интересно симулирует классы с помощью функций. Если вы не знакомы с Javascript, то, что здесь происходит – это определение класса, у которого есть определенные свойства (доступ к которым получается с помощью ключевого слова this), и некоторые методы (которые в Javascript помещены в прототип функции). Просто запомните их как классовые методы. Также не забывайте, что способ, с помощью которого мы будем их использовать, заключается в том, что мы сначала передадим (forward) все логические элементы по одному, а потом вернем их обратно (backward) в обратном порядке. Вот реализация этого:

var multiplyGate = function(){ };
multiplyGate.prototype = {
  forward: function(u0, u1) {
    // сохраняем указатели для ввода сегментов u0 и u1 и выходного сегмента utop
    this.u0 = u0; 
    this.u1 = u1; 
    this.utop = new Unit(u0.value * u1.value, 0.0);
    return this.utop;
  },
  backward: function() {
    // берем градиент в выходном сегменте и связываем его с 
    // локальными градиентами, которые мы дифференцировали для логического элемента умножения заранее 
    // после этого прописываем эти градиенты в этих сегментах.
    this.u0.grad += this.u1.value * this.utop.grad;
    this.u1.grad += this.u0.value * this.utop.grad;
  }
}

Логический элемент умножения берет два сегмента, каждый из которых содержит значение, и создает сегмент, который сохраняет его результат. Градиенту присваивается в качестве начального значения ноль. Потом, обратите внимание, что при вызове функции backward мы получаем градиент из результата сегмента, который мы создали в процессе переднего прохода (который теперь, надеюсь, будет иметь свой заполненный градиент) и умножаем его на локальный градиент для этого логического элемента (цепное правило!). Этот логический элемент выполняет умножение (u0.value * u1.value) при переднем проходе, поэтому вспоминаем, что градиент по отношению к u0 равен u1.value и по отношению к u1 равен u0.value. Также обратите внимание, что мы используем += для прибавления к градиенту при функции backward. Это, возможно, позволит нам использовать результат одного логического элемента несколько раз (представьте себе это как разветвлении линии), так как оказывается, что градиенты по этим ветвям просто суммируются при расчете окончательного градиента по отношению к результату схемы. Остальные два логических элемента определяются аналогичным образом:

var addGate = function(){ };
addGate.prototype = {
  forward: function(u0, u1) {
    this.u0 = u0; 
    this.u1 = u1; // сохраняем указатели для ввода сегментов
    this.utop = new Unit(u0.value + u1.value, 0.0);
    return this.utop;
  },
  backward: function() {
    // логический элемент сложения. Производная по отношению к обоим результатам равна 1
    this.u0.grad += 1 * this.utop.grad;
    this.u1.grad += 1 * this.utop.grad;
  }
}
var sigmoidGate = function() { 
  // вспомогательная функция
  this.sig = function(x) { return 1 / (1 + Math.exp(-x)); };
};
sigmoidGate.prototype = {
  forward: function(u0) {
    this.u0 = u0;
    this.utop = new Unit(this.sig(this.u0.value), 0.0);
    return this.utop;
  },
  backward: function() {
    var s = this.sig(this.u0.value);
    this.u0.grad += (s * (1 - s)) * this.utop.grad;
  }
}

А теперь давайте рассчитаем градиент: просто повторим все в обратном порядке и вызовем функцию backward! Вспоминаем, что мы сохранили указатели в сегменты, когда выполняли проход вперед, поэтому у логического элемента есть доступ к его исходным значениям, а также к выходному сегменту, который он ранее создал.

s.grad = 1.0;
sg0.backward(); // записывает градиент в axpbypc
addg1.backward(); // записывает градиент в axpby и c
addg0.backward(); // записывает градиент в ax и by
mulg1.backward(); // записывает градиент в b и y
mulg0.backward(); // записывает градиент в a и x

Обратите внимание, что первая строка устанавливает градиент на выходе (самый последний сегмент) в значение 1.0 для запуска цепи градиента. Это можно интерпретировать, как толчок на последний логический элемент с силой равной +1. Другими словами, мы тянет всю схему, заставляя ее прикладывать силы, которые увеличат выходное значение. Если бы мы не задали ему значение 1, все градиенты рассчитывались бы как нулевые ввиду умножения согласно цепному правилу. В конечном итоге, давайте заставим исходные значения реагировать на рассчитанные градиенты и проверим, что функция увеличилась:

var step_size = 0.01;
a.value += step_size * a.grad; // a.grad равно -0.105
b.value += step_size * b.grad; // b.grad равно 0.315
c.value += step_size * c.grad; // c.grad равно 0.105
x.value += step_size * x.grad; // x.grad равно 0.105
y.value += step_size * y.grad; // y.grad равно 0.210

forwardNeuron();
console.log('circuit output after one backprop: ' + s.value); // выводится результат 0.8825

Успех! 0.8825 выше, чем предыдущее значение, 0.8808. Наконец, давайте проверим, что мы правильно выполнили обратное распространение ошибки, проверив числовой градиент:

var forwardCircuitFast = function(a,b,c,x,y) { 
  return 1/(1 + Math.exp( - (a*x + b*y + c))); 
};
var a = 1, b = 2, c = -3, x = -1, y = 3;
var h = 0.0001;
var a_grad = (forwardCircuitFast(a+h,b,c,x,y) - forwardCircuitFast(a,b,c,x,y))/h;
var b_grad = (forwardCircuitFast(a,b+h,c,x,y) - forwardCircuitFast(a,b,c,x,y))/h;
var c_grad = (forwardCircuitFast(a,b,c+h,x,y) - forwardCircuitFast(a,b,c,x,y))/h;
var x_grad = (forwardCircuitFast(a,b,c,x+h,y) - forwardCircuitFast(a,b,c,x,y))/h;
var y_grad = (forwardCircuitFast(a,b,c,x,y+h) - forwardCircuitFast(a,b,c,x,y))/h;

Таким образом, все это дает те же значения, что и градиенты обратного распространения ошибки [-0.105, 0.315, 0.105, 0.105, 0.210]. Отлично!

Я надеюсь, вам понятно, что даже несмотря на то, что мы рассмотрели только пример с одним нейроном, код, который я привел выше, представляет собой довольно простой способ вычисления градиентов произвольных выражений (включая очень глубокие выражения). Все, что вам нужно сделать – это написать небольшие логические элементы, которые будут вычислять локальные простые производные по отношению к их исходным значениям, связать их в график, выполнить проход вперед для вычисления выходного значения, после чего выполнить обратный проход, который свяжет градиент по всему пути к исходному значению.

Автор: Irina_Ua

Источник