В продолжении популярного цикла статей о том, что 30 строк джаваскрипта достаточно каждому, предлагаю Вашему вниманию перевод статьи Мэтью P01 Генри о его последней работе:

(далее текст от первого лица, все «я» относятся к P01)
Мотивация
Около года назад Нотч написал на джаваскрипте леталку по миру майнкрафтра с процедурными текстурами, камерой и эффектом тумана общим весом всего 4 кило… Смотрелась она прикольно и работала живенько. Её код заточен под скорость, т.е. потратив немного усилий, её было реально ужать до 2-х или даже 1-го килобайта.
Месяц назад, я зарелизил Вульфенштейника, и реакция сообщества была весьма воодушевляющая. Поэтому я сделал следующий шаг и перешёл к полноценному 3D.
Исходники
<body onload=setInterval(F=";t+=.1;Q=Math.cos;for(x=n=c.height=300;x-=4;)for(y=n;y-=4;d.fillRect(x,y,E,Z^z?4:E))for(D=0;(E=4-D/2)&&F<F[(t+D*Q(T=x/n-.5+Q(t/9))&7)*8|(Z=3.7+D*Q(T-8)&7)*4|(6.5-D*y/n-E)];z=Z)D+=1/8",t=55),d=c.getContext('2d')><canvas id=c>Вуаля! 252 байт шаманства с воксельным 3D миром, камерой и эффектом тумана.
Версия 248 для понтов
<body onload=setInterval(F=";t+=.1;Q=Math.cos;for(x=n=c.height=300;x-=4;)for(y=n;y-=4;c.getContext('2d').fillRect(x,y,E,Z^z?4:E))for(D=0;(E=4-D/2)&&F<F[(t+D*Q(T=x/n-.5+Q(t/9))&7)*8|(Z=3.7+D*Q(T-8)&7)*4|(6.5-D*y/n-E)];z=Z)D+=1/8",t=55)><canvas id=c>Немного более медленная версия Миникрафта в 248 байт, потому что могу! Всё то же самое, только работает медленнее.
Как ?
Вам наверняка интересно, как 3D движок, траектория полёта камеры и сам трёхмерный мир умещаются в 252 байтах html и джаваскрипта. Это адская смесь разных красивых и грязных приёмов; о некоторых из них и пойдёт речь ниже.
Плечи карликов
На самом деле, Миникрафт стоит на плечах своих миниатюрных предшественников — Вульфенштейника, Бури в стакане и Райончика. Многие приёмы, использующиеся тут, уже были описаны ранее вместе с этими релизами.
Отрисовка
Учитывая ограничение размера этой демки, для красивой отрисовки небыло места. Пришлось использовать грубую трассировку лучей с фиксированным шагом.
Если Вам интересно, что скрывается за этими заумными словами — то всё довольно просто. Функция, представляющая мир, который Вы хотите нарисовать, фактически вычисляется для каждой точки в пространстве между камерой и точками, которые Вы реально рисуете. Другими словами, Вы вызываете эту жирную функцию тысячи, сотни тысяч раз за кадр без какого-либо намёка на оптимизацию быстродействия.
Разрешение
Разрешение элемента canvas по умолчанию — 300x150. Установка ширины или высоты канваса очищает его и сбрасывает его установки. Если Вы хотите получить наибольшое разрешение наименьшей ценой, наилучшим способом будет устанавливить высоту в 300 в каждом кадре.
Итак, мы имеем канвас 300x300. Однако выбранный метод отрисовки слишком медленный для такого количества лучей. Посему, разделив разрешение на 4, мы будем трассировать только 75x75 = 5,625 лучей. Проходя луч с шагом 1/8 пока не будет достигнут непрозрачный блок или расстояние в 8 единиц, мы получим максимум 75x75x80 = 450,000 проверок за кадр.
Мир из строчки
При таком размере у Вас совершенно нет места, чтобы сгенерировать, сохранить или использовать динамическую карту расстояний в качестве карты мира, поэтому приходится пользоваться единственными доступными данными: исходным кодом.
Поместив код главного цикла в переменную F, мы получаем доступ к его строковому представлению и используем его как карту прозрачных/непрозрачных блоков в 3D решётке.
Так как код короткий, данных в нём хватило лишь на мир размером 8х8х8, использующий первые 64 символа основного цикла в качестве информации о 512 вокселях. Изучив ASCII коды в этой строке, я решил считать непрозрачным блоком любой символ, предшествующий точке с запятой в таблице ASCII, включительно. Другими словами, любой из символов !"#$%&'()*+,-./0123456789:; означает непрозрачный блок. Этот выбор позволил получить в карте сквозную дыру, чем в свою очередь упростил траекторию камеры.
Т.о., проверка пересечения в Миникрафте выглядит очень просто:
// F = the source code of the main loop
';' < F[x + z * 4 + y * 8]
Кстати о точке с запятой, внимательный читатель мог заметить в исходнике одну странную деталь:

Видите, код основного цикла начинается с точки с запятой? Эта на первый взгляд бесполезная точка с запятой позволяет выиграть дополнительный байт, сократив и так довольно компактную проверку пересечения до:
F < F[x + z * 4 + y * 8]
Трассировка лучей и камера
Как было сказыно выше, в 3D карте получился сквозной проём, идеальный для пролёта камеры. Лучи бросаются от камеры в пределах пирамиды видимости для каждого пикселя, затем мы постепенно проверяем все точки вдоль луча на предмет пересечения с картой, пока оно не будет найдено, или пройденное растояние не превысит допустимый максимум. Чем дальше мы продвинулись вдоль луча, тем более яркий оттенок серого будет назначен соответствующему пикселю.
for(x=n=c.height=300;x-=4;)
for(y=n;y-=4;/* тут красим пиксель в позиции x,y оттенком D */)
for(D=0;/* тут проверяем на пересечение с картой в позиции X, Y, Z */;z=Z)
D+=1/8
Внешние циклы бегают по всем x и y пикселей и закрашивает их полученным оттенком серого D. Внутренний цикл шагает вдоль луча, соответствующего пикселю на позиции x, y пока не буден найден непрозрачный блок.
Трёхмерные X, Y, Z координаты текущего положения на луче вычисляются следующим образом:
// ниже E=4-D/2
(t+D*Q(T=x/n-.5+Q(t/9))&7)*8|(Z=3.7+D*Q(T-8)&7)*4|(6.5-D*y/n-E)
Что на самом деле вычисляет Y * 8 | Z * 4 | X. Если подробнее, то:
// угол направления камеры
cA = Math.cos(t/9)
// угол отклонения луча
rA = x / h - .5 + cA
// D - расстояние, которое мы отшагали вдоль луча
// камера двигается по прямой вдоль оси Y
Y = D * Math.cos(rA) + t
Z = D * Math.sin(rA) + 3.7
X = D * ( y / h - .5) + 2.5
Дизеринг, туман и оттенки серого
По умолчанию у canvas установлен чёрный fillStyle. Для его изменения не хватает места, посему приходится искать другой способ реализовать палитру. Оттенки серого в Миникрафте получаются из прямоугольников с дробной шириной и высотой. Суб-пиксельные размеры вызывают сглаживание, которое делает рёбра прямоугольников полупрозрачными. Вот так просто. Рисуя по одному прямоугольнику для каждого пикселя, мы фактически получаем некую разновидность дизеринга.
Освещение в демке использует тот же трюк, что и Райончик с Вульфенштейником. Для определения направления нормали поверхности в одну или другую сторону сравниваются целые части Z координат точек на луче до и после определения пересечения с непрозрачным блоком. Помните основной цикл?
;t+=.1;Q=Math.cos;for(x=n=c.height=300;x-=4;)for(y=n;y-=4;d.fillRect(x,y,E,Z^z?4:E))for(D=0;(E=4-D/2)&&F<F[(t+D*Q(T=x/n-.5+Q(t/9))&7)*8|(Z=3.7+D*Q(T-8)&7)*4|(6.5-D*y/n-E)];z=Z)D+=1/8
код, отвечающий за хранение и сравнение целых частей координат Z, в нём находится в выражениях Z^z?4:, Z= и z=Z.
Магия чисел
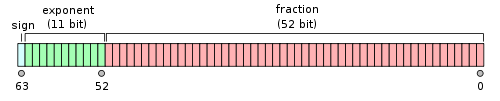
Мы все знаем, что числа с плавающей запятой неоптимальны для приложений, где требуется точное представление чисел. Стандарты IEEE-754 основаны на двоичной записи и степенях двойки, что приводит к ошибкам округления десятичных чисел.
В джаваскрипте, как и во многих других языках программирования, 0.1 + 0.2 = 0.30000000000000004. Это неудобно во многих ситуациях, однако, когда Вы имеете дело исключительно со степенями двойки, IEEE 754 играет Вам на руку и позволяет исполнить пару трюков.
Например, в циклах рассчёта лучей, приведенных выше,
for(x=n=c.height=300;x-=4;)
for(y=n;y-=4;/* тут красим пиксель в позиции x,y оттенком D */)
for(D=0;(E=4-D/2)&&F<F[ ... ];z=Z)
D+=1/8
мы можем легко заметить, что D достигло 8, т.к. выражение (E=4-D/2) обращается в 0, что в свою очередь эквивалентно false и останавливает цикл.
Значение E соответствует размеру прямоугольника, который мы рисуем для этого луча, и одновременно служит для вычисления координаты Х для точки на луче. В общем и целом этот фокус экономит 3 байта.
Грязная тригонометрия
Чтобы выиграть 4 байта в коде, который использует Math.cos и Math.sin, создаётся ссылка на Math.cos, а «синус» получается добавлением 8 к аргументу. Ошибка такой аппроксимации не превышает 0.15 радиан.
Отзывы
Отзывы и предложения собираются на страничке Миникрафта на сайте Pouet.net.
Автор: makc3d
