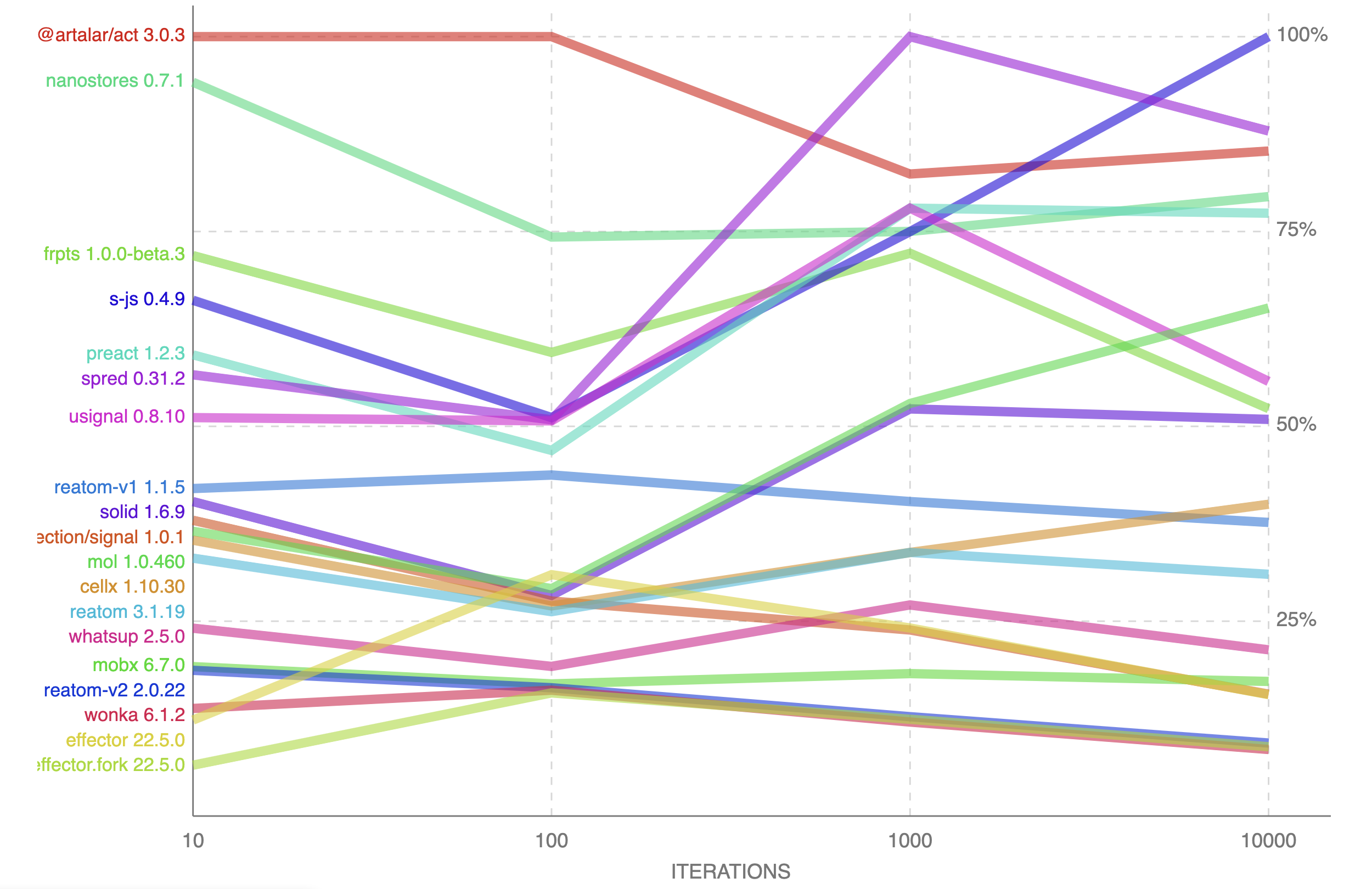
Всем привет, меня зовут Артём Арутюнян, и я уже пять лет изучаю реактивное программирование. Меня задела недавняя статья, Big State Managers Benchmark, в которой моя библиотека Reatom заняла лишь третье место (скорее второе, ну да ладно) и я решил написать самую эффективную реализацию реактивных состояний, убрав лишние фичи, сфокусировавшись на простоте и производительности.
Немного поэкспериментировав я добился удивительных результатов, в сто строк (0.3KB gzip) уместив максимально простое апи, которое позволяет подключаться к React и Svelte без дополнительных адаптеров. Но самое главное, найденный алгоритм фундаментально покрывает любые краевые случаи условных переподписок зависимых вычислений, с которыми подавляющее большинство популярных библиотек не справляется и дают глитчи.
Если вам интересны детали реализации — прошу под кат.
Идея
Сразу выложу карты на стол и опишу ключевую оптимизацию, а потом разберём алгоритм поэтапно. Промежуточные вычисляемые зависимости между подписчиками и мутируемыми листьями графа не обязаны иметь и инвалидировать ссылки на другие компьютеры, которые их используют — достаточно иметь список своих зависимостей для простой мемоизации. Для распространения изменений подписчики должны храниться напрямую в мутируемых листовых нодах. Иначе говоря, граф вычисляемых зависимостей можно сделать не двунаправленным, а однонаправленным, что сильно сокращает расходы на его инвалидацию (распространение изменений и обновление). Двунаправленными остаются только краевые части графа.
Читаемые исходники с наглядной типизацией и комментариями можно найти тут.
Текущая ситуация
Удивительно, что в 2023 мы открываем новые границы производительности реактивности. Не первый раз убеждаюсь, что тема эта для нас новая и не изученная. Можно понять, реактивность ортодоксальна компайл-тайму, ведь её смысл — вынесение связей модулей из статического описания в рантайм. Думаю, поэтому за неё ещё не брались серьёзно «большие дядьки», которые предпочитают копаться в компиляторах. Идея шатать графы в рантайме на каждый чих кажется безумной. Особенно учитывая количество необходимой памяти на каждую ноду — двунаправленные связи, флаги дертичекинга, кеши — всё это может потреблять ресурсов заметно больше обслуживаемых вычислений. Стоит оно того?
Ещё год назад фронтом производительности среди реактивных библиотек был пятилетний CellX, потом на сцену вышел Preact со своими сигналами и неплохо так всех порвал. Хотя из статьи по первой ссылке вы могли узнать, что реактивность в преакте глючная и может пропускать некоторые вычисления с некорректными данными. И вот, я представляю вам венец корректности и оптимальности реактивных состояний — Act. У каждой ноды всего один список зависимостей, и интеджер для тривиального кеширования, это практически всё.
Стоит подчеркнуть, что Act — самая оптимальная библиотека в вопросах скорости создания связей, обновления и размера бандла, а также простоты внутренней реализации. Конечно, есть случаи, в которых Act будет не самым быстрым решением, а результаты одних и тех же бенчмарков могут отличаться от движка к движку. Во второй половине статьи мы разберём возможные трейдофы.
Алгоритм
▍ Пример
Для подробного разбора давайте возьмём реальный пример и определимся с терминологией.
Пример. У нас есть список валют и их отношений к другим валютам. Есть товар и его стоимость зависит от выбранной валюты. Есть список товаров и их сумма.
export const currencies = act({ USD: { EUR: 1.1 }, EUR: { USD: 0.9 } });
export const currency = act("USD");
export const products = act([]);
export const sum = act(() =>
products().reduce((acc, { price, count }) => acc + price() * count(), 0)
);
export const createProduct = (dto) => ({
...dto,
count: act(1),
price: act(() => currencies()[currency()][dto.currency] * dto.cost),
});
export const addProduct = (dto) =>
products([...products(), createProduct(dto)]);
▍ Граф
Реактивные связи образуют граф, края которого, с одной стороны mutable / writable / base / value / leaf (currencies, currency, products, count), а с другой стороны подписчики / subscribers / listeners / effects, которые являются потребителями вычислений. Нейминг в разных библиотеках отличается, но промежуточные вычисляемые ноды (sum, price) практически везде называются computed или combine, главная сложность кроется именно в них.
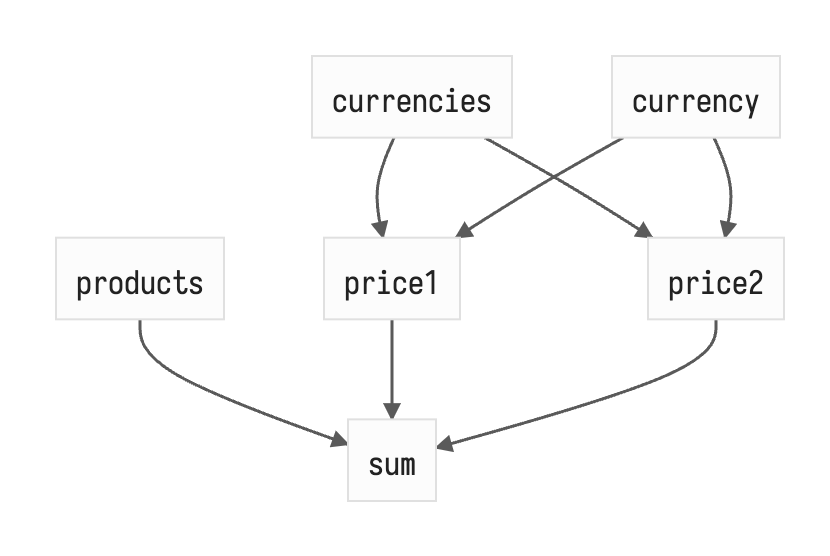
Так как в вычисляемую ноду может заходить сразу несколько связей, а из базовой ноды может исходить несколько связей, мы получаем ациклически направленный граф (DAG), который отличается от дерева (одной из самых простых и эффективных графовых структур) тем, что во время его наивного обхода есть риск несколько раз зайти в одну и ту же ноду, что может быть чревато лишними вычислениями. Вот описание рекурсивного обхода в глубину (DFS) зависимых нод в случае смены currency:
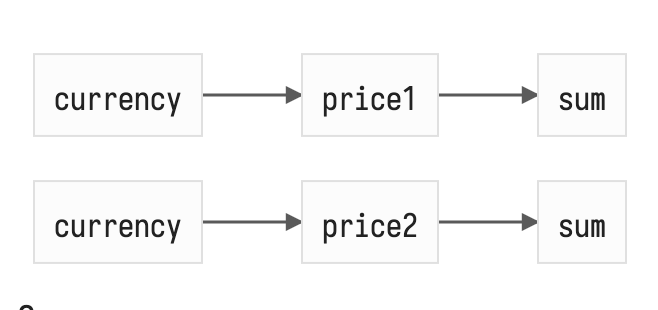
Сама картинка страшно не выглядит, но стоит учитывать, что это не отображение графа зависимостей, а отображение процесса его обхода, в котором мы дважды заходим в sum и первый раз «приносим» новое значение price1 ещё не обновив price2 из-за чего до нотификации price2 --> sum сумма будет высчитана неверно, что в некоторых системах может породить ошибки представления или даже вычисления (throw TypeError). Но если ошибок можно избежать, лишние вычисления будут требовать лишних накладных расходов, нас же интересует возможность автоматической оптимизации и отбрасывания лишнего. Это классическая проблема для топологической сортировки и её разновидностей: можно помечать ноды «посещёнными» (классический dirty checking), можно рассчитывать для каждой ноды веса (вес тем больше чем позже нода была создана) и сортировать по ним релевантные ноды графа до его обхода. Можно придумать десяток комбинаций разнообразных приёмов из теории графов. Но в продвинутых системах, где реактивность старается быть прозрачной и позволяет гибче её описывать, используя нестатическое апи combine($a, $b, (a, b) => a + b), а динамическое computed(() => a() + b()), появляются ДИНАМИЧЕСКИЕ ГРАФЫ.

Динамический граф — это граф, чьё состояние (отношения нод) может меняться во время его обхода. Сложно писать без эмоций, эта штука, которая разобьёт тебе лицо любым неловким поворотом своих бесконечных пируэтов. Динамический граф напрочь отменяет многие правила и паттерны, применимые для оптимизации классических графов, заметно усложняя всю систему, особенно учитывая, что у нас DAG.
Так зачем оно? Дело в удобности конечного апи. Любые либы с мутабельным стейтом под Proxy позволяют использовать свойства объектов и прозрачно подписываться на их изменения — это удобно для разработчика приложения, но совсем неудобно для разработчика библиотеки, т. к. убирается явное использование его методов, чтение и подписки просто происходят в произвольном порядке внутри функции пользователя. Какие условия там могут быть описаны, неизвестно, и статически не могут быть проанализированы: ифы, тернарки, форы и вайлы, колбеки. Хотя тот же switchMap из декларативного Rx позволяет менять структуру графа, чтобы убрать из рыксы глитчи придётся тоже поднапрячься. Чтобы кешировать переподписки между вызовами пользовательских вычисляемых функций, применяется счётчик вызовов, который позволяет просто сравнивать предыдущий и новый список используемых зависимостей и на основе этого принимать решение о инвалидации подграфа зависимостей… Ух, ещё не устали? Может, визуализации не хватает? А давайте остановимся и не будем погружаться во все вариации того что, как и зачем нужно делать в реактивных графах и какие сюрпризы там скрываются, это тема как минимум на серию постов. Есть множество готовых библиотек, чей код можно поизучать. Отойдём немного назад. Поэтапно погружаясь в проблемы и фичи реактивных графов, мы строили новые предположения на основе предыдущих, но что если нам вовсе не нужно кеширование и тогда, не нужна его инвалидация?
▍ Выворачиваем связи
О чём нужно задуматься, кому вообще нужны эти вычисления? При ленивом подходе ответ очевиден — подписчикам. Но если подписчик — источник истины о необходимой структуре зависимостей, а изменения могут начинаться и распространяться только в определённом типе нод — мутабельных листьях графа, зачем нам вообще хранить и инвалидировать связи в промежуточных нодах? С одной стороны логично, что если у нас уже есть граф и нам нужно связать его разные края — нам нужны двунаправленные связи, это примитивное решение для деревоподобных (tree-like) структур, но у нас же уже есть DAGи в производных нодах и это всё динамическое! Учитывая, что в нашей системе точки входа и выхода чётко разделены и находятся по краям — можно соединить только эти края и оставить в покое все замкнутые внутренние ноды.
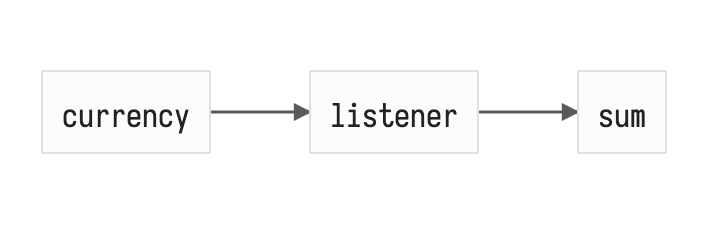
Стало проще, да? Кешировать только sum уже намного проще. Если рисовать все связи, то было/стало выглядит так.
push (дерти чекинг) + pull (кеш) связи
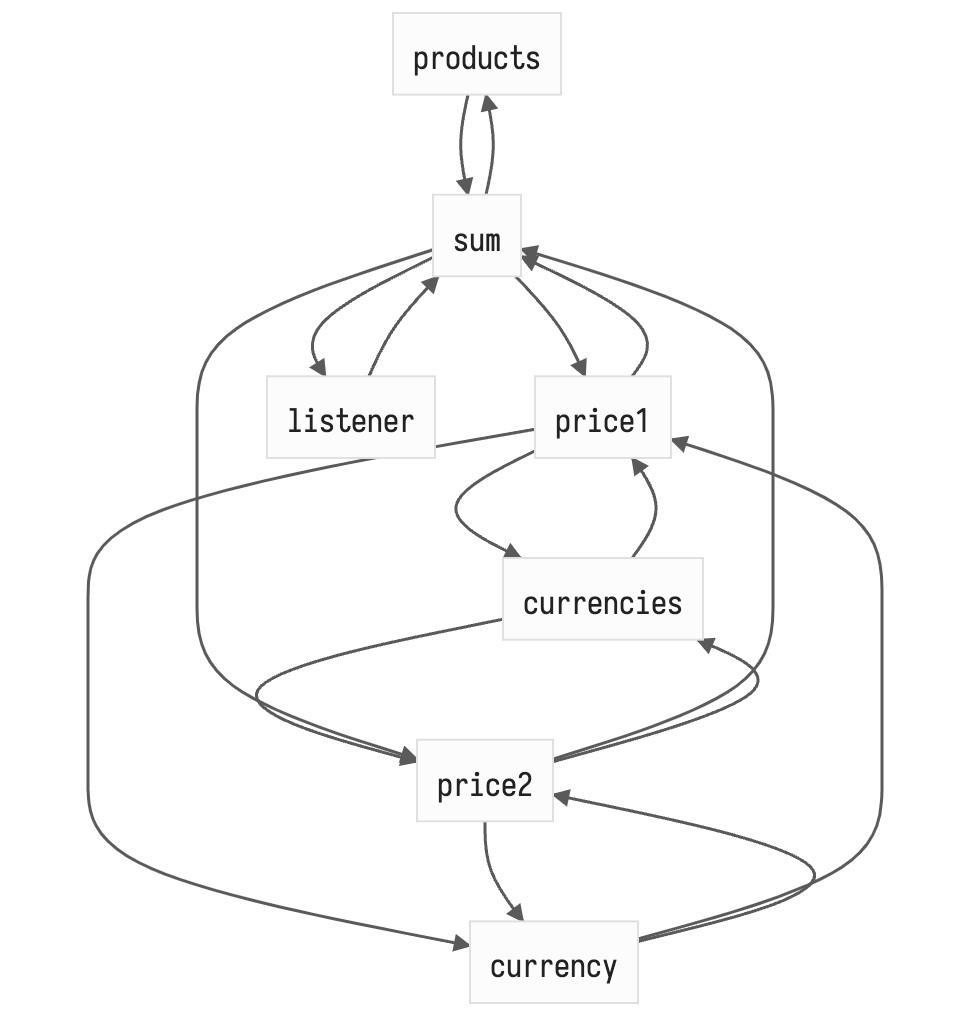
notifications (сайд-эффекты) + pull (кеш) связи
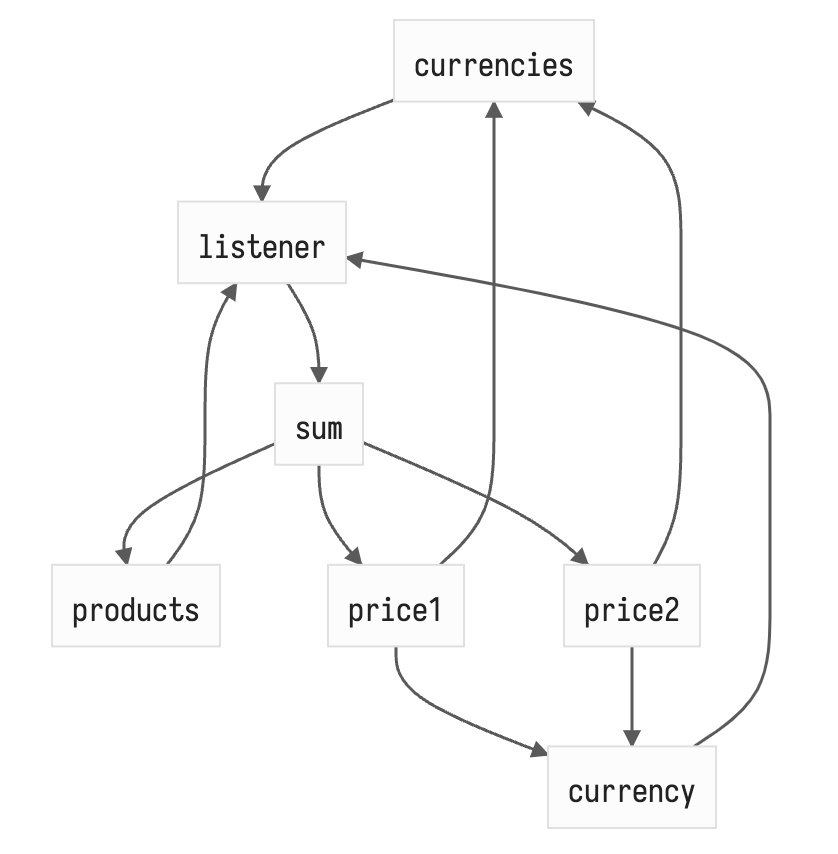
Связей в полтора раза меньше и эта разница будет уменьшаться с ростом числа продуктов! Как видно, кеш связи (pull) остались — это простая мемоизация — когда у вычисляемой ноды пытаются получить значение, она сначала проходится по старому списку зависимостей и сравнивает последнее полученное состояние зависимости и текущее, если что-то различается — переданную пользователем функцию нужно перевызвать, иначе отдаём свой старый стейт. Важно отметить, что для предотвращения инвалидации вычисляемых нод по несколько раз (например, если бы currencies был вычисляемым) мы храним версию текущего обхода в каждой ноде и сравниваем при каждом заходе — это максимально простой и легковесный кеш, который очень просто инвалидировать просто инкрементом глобальным счётчиком обходов.
▍ Трейдофы
Пытливый читатель может задаться вопросом, если флаг инвалидации глобальный для всех, то обновление одного графа, помечает неактуальными вычисляемые ноды всех остальных графов и при попытке их простого чтения придётся проходить по всему pull кешу. Да, но тут нужно оценить реальный оверхед этой неоптимальности. В полностью реактивной системе мы не читаем данные просто так, это происходит только при обновлениях — тогда чтение релевантно, и актуализация и так сбрасывается, чтобы проверить влияние обновления на вычисляемые ноды. Мои эксперименты показали что инвалидация pull кеша очень дешёвая операция и её избыточные перевызовы лучше, чем хранение и инвалидация двунаправленных связей для каждого computed.
Если пофантазировать над другими возможными графами состояний, то можно представить более сложную структуру товара и при изменении count в одном товаре для пересчёта суммы нужно будет пройтись по всем нодам всех товаров, что при наличии в них многоуровневых вычисляемых нод может вести к избыточным вычислениям, но на моей практике это не такой частый случай и однонаправленный граф тут всё равно будет, скорее всего, дешевле двунаправленного.
Уточню про инвалидацию связей динамического графа, это же самая большая проблема. При добавлении нового товара, в зависимости от его очереди в общем списке и используемым алгоритмам сравнения списка зависимостей в двунаправленном графе, скорее всего, придётся пересоздавать одни и те же связи или плодить достаточно много промежуточных кешей уникального списка (Set) — оверхед. В случае с notification + pull подходом нам нужно инвалидировать меньше связей, но Act вообще никакие сравнения не делает, всё проще.
В современном мире не всегда память — узкое место. Мобильные телефоны — критический сегмент рынка — используют SoC, которые часто имеют хорошую шину между памятью и процессором. Иногда лишние вычисления могут стоить дороже выкидывания старой и использования новой памяти. В Act, когда краевая нода обновляется — она пушит в общую очередь нотификации список своих зависимостей и создаёт его заново — пустой. Когда каждый подписчик будет затягивать новые значения, он неизбежно зайдёт в обновлённую ноду и добавится в новый список зависимостей. Всё. Никаких сравнений и дополнительных кешей — просто пересоздание части графа from scratch. Преимущество такого подхода в том, что при добавлении новой ноды (нового товара, например) подписчик не делает никакой новой работы — он также проходит по всему графу и добавляется ко всем заново. А как он добавляется заново к старым нодам? В них используется Set для списка сайд-эффектов, к счастью, в JS это ordered linked list с константной сложностью доступа.
▍ Ленивые отписки могут привести к утечкам памяти
Но есть в этом алгоритме потенциальная возможность для утечки памяти. Как происходят отписки? Подписчик проходится по всему графу и удаляет себя из краевых нод — не максимально оптимально, но терпимо. А если мы удалили товар из корзины? Если ссылка на товар полностью исчезает — GC её съест вместе со списком подписчиков. Но если товар переносится в список избранного, то ссылка на старого подписчика для sum там всё ещё остаётся и будет очищен только при обновлении товара и переинвалидации списка. Словить такую ситуацию не просто и тем более заставить это линейно течь, но мы же хотим не заставлять думать пользователя библиотеки о графах и их инвалидации самому, поэтому давайте исправим это. Пусть при добавлении в список подписчиков краевой ноды (writable) подписчика, самому подписчику сохраняется краевая нода в простой массив. Тогда, при инвалидации подписчика (обновлении списка продуктов) он может пройтись по старому списку краевых нод и удалить себя (благо Set.prototype.delete константный), а потом собрать заново, как говорилось выше. Обновлённый граф немного сложнее.
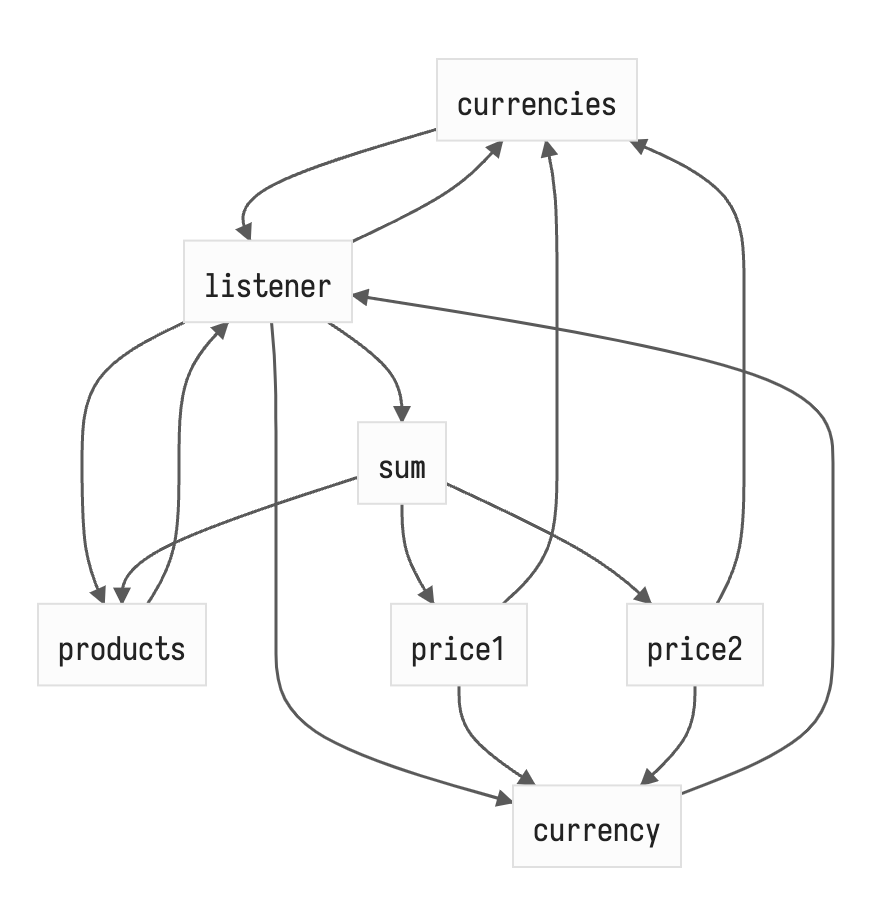
Но он всё ещё легче и эта реализация всё ещё производительней других решений в большинстве случаев.
Итоги
По ссылке на бенчмарк из первой статьи теперь можно найти и Act, чаще всего он показывает наилучшие результаты, а главное, работает максимально корректно и не содержит ошибок инвалидации списка зависимостей. В моём бенчмарке акт тоже показывает, в общем, лучшие результаты.
Интересно, то что этот notification-pull алгоритм с пересозданием нод очень простой по сравнению с классическим дерти чекингом, двунаправленными связями и их инвалидацией, размер бандла тому в подтверждение. Хотя после всех допиливаний и улучшений читаемости 0.3KB gzip превратились в 0.4KB brotli, но результат всё равно впечатляющий.
Надеюсь, что эта статья вскоре станет устаревшей, потому что мы найдём новые простые и эффективные способы оптимизации наших библиотек и приложений. В любом случае хочется порекомендовать попробовать Act, благодаря размеру он может прекрасно помочь добавить интерактивность на лендинг и как уже говорилось в начале статьи — он легко интегрируется с React и Svelte без дополнительных адаптеров, предсказуем и очень прост в использовании. Ну а если вам нужно решение с ещё большими перспективами по стабильности и масштабированию (лайфсайкл хуки, продвинутый дебаг, контекстно-зависимые процессы) — reatom.dev, там апи не сильно сложнее и есть уже приличная экосистема.
Автор: Артём Арутюнян






