Калькулятор на типах TypeScript

TypeScript

В последнее время TS стал де-факто стандартом во фронтенд-разработке. Его достаточно просто начать использовать, и он приносит неоценимую пользу в любых web-приложениях. Но используя его, мы часто даже не задумываемся, насколько на самом деле это мощный инструмент. В большинстве ситуаций нам хватает базовых возможностей TS-а. Но иногда нам случается определить узкий и нестандартный тип. В этом случае можно либо ослабить типы с помощью any или unknown, либо попробовать решить непростую порой головоломку. В этой статье мы решим несколько интересных головоломок с типами.

Заранее предупреждаю, что хабр не умеет подсвечивать TS, так что с подсветкой иногда могут быть проблемы :)

Что там с типами?

Случай на код-ревью

Как-то раз на код-ревью я увидел строку

type itemType = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13;

И тут я подумал, что интересно было бы сделать тип NumbersRange<FROM, TO> для генерации таких юнионов.

Базовая реализация

Сначала реализуем тип, принимающий один параметр-дженерик и возвращающий юнион числовых литералов от 0 до переданного числа:

type NumbersRange<
    TO extends number,
    RESULT extends unknown[] = [0],
    > = RESULT['length'] extends TO
    ? [...RESULT, TO][number]
    : NumbersRange<TO, [...RESULT, RESULT['length']]>;

По сути тип выглядит как рекурсивная функция, проходящая от 0 до заданного числа, собирающая все промежуточные числа в кортеж, и возвращающая юнион по этому кортежу. Для итерации используем хвостовую рекурсию по длине кортежа RESULT .

В каждом вызове проверяем, достигло ли количество элементов в кортеже заданного изначально числа TO: RESULT['length'] extends TO и либо возвращаем юнион по кортежу с вставленным последним элементом TO (для получения юниона по кортежу мы обращаемся к его элементу с неопределенным индексом: [number] , и получаем юнион всех типов, хранящихся в кортеже). Либо вызываем эту же функцию, положив в RESULT очередное число по порядку.

Все это работает благодаря возможности обращаться к свойствам типа (в данном случае ['length'] у кортежа). Например, type Two = [0, 0]['length']; — Two будет равен литералу 2.

Улучшаем реализацию

В примере выше есть две проблемы: нельзя задать начало промежутка, а также не обрабатывается случай, когда промежуток состоит только из одного элемента. Имея инструменты из предыдущего примера, это сделать достаточно просто.

type ZERO = 0;
type Iterate<tuple extends ZERO[]> = [...tuple, 0];

type NumbersRange<
    FROM extends number,
    TO extends number
    > = TO extends FROM 
    ? FROM
    : NotEmpytNumbersRange<FROM, TO>;

type NotEmpytNumbersRange<
    FROM extends number,
    TO extends number,
    ITERATOR extends ZERO[] = [],
    > = ITERATOR['length'] extends FROM
    ? SequenceNumbersRange<TO, ITERATOR>
    : NotEmpytNumbersRange<FROM, TO, Iterate<ITERATOR>>;

type SequenceNumbersRange<
    TO extends number,
    ITERATOR extends ZERO[],
    RESULT extends unknown[] = [],
    > = ITERATOR['length'] extends TO
    ? [...RESULT, TO][number]
    : SequenceNumbersRange<
        TO, 
        Iterate<ITERATOR> ,
        [...RESULT, ITERATOR['length']]
    >;

Калькулятор

Реализуя NumbersRange, я сильно удивился возможностям типов TS. Как оказалось, система типов TS претендует на тьюринг-полноту. Поэтому я решил пойти дальше, и реализовать на типах что-нибудь интересное. Например, калькулятор!

Что будем реализовывать?

Я задумал реализовать такой тип - функцию:

type Calculate<EXPRESSION>;

// type calculationResult = Calculate<'7+5-2*2+1'> 
// calculationResult is 9 alias

План реализации будет такой:

• Научиться получать следующий числовой литерал

• Научиться складывать литералы, вычитать, умножать

• Распарсить строковое выражение

• Обойти дерево и провести все требуемые операции

Получаем следующий и предыдущий числовой литерал

Чтобы получить следующий числовой литерал используем рекурсию по длине кортежа с нулями:

type Increase<
	A, 
	ACC extends Array<number> = []
> = ACC['length'] extends A
    ? [...ACC, 0]['length']
    : Increase<A, [...ACC, 0]>;

Для получения предыдущего литерала немного поменяем код: итерируемся, пока следующий элемент не будет равен переданному параметру

type Decrease<
	A,
	ACC extends Array<number> = []
> = [...ACC, 0]['length'] extends A
    ? ACC['length']
    : Decrease<A, [...ACC, 0]>;

Арифметические операции

Сложение двух чисел зададим как рекурсию, заданную двумя правилами:

• Сложение нуля с любым числом дает это же число

• Сложение A и B это сложение (A - 1) и (B + 1)

type ZERO = 0;
type Add<A, B> = A extends ZERO ? B : Add<Decrease<A>, Increase<B>>;

Вычитание двух чисел зададим как рекурсию, заданную двумя правилами:

• Вычитание нуля из любого числа дает это же число

• Вычитание B из A это вычитание (B - 1) из (A - 1)

type Sub<A, B> = B extends ZERO ? A : Sub<Decrease<A>, Decrease<B>>;

Умножение A на B сделаем как сложение числа A B раз:

type Mul<A, B, I = 0, Result = 0> = I extends B 
? Result 
: Mul<A, B, Increase<I>, Add<Result, A>>;

Тут мы проходим в цикле по I от 0 до В и каждый раз добавляем в переменную Result число A.

Парсим строковое выражение

Строковое арифметическое выражение будем представлять в виде дерева. Например, выражение 3 + 5 - 2 будет представляться таким деревом:

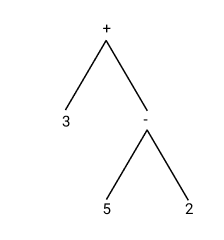
type Operation = '+' | '-' | '*';

type CalcExpressionNode = {
    left: CalcEpression,
    right: CalcEpression,
    operation: Operation
}

type CalcEpression = CalcExpressionNode | number;

Тут мы рекурсивно определяем тип CalcEpression, с помощью которого мы будем хранить распаршенное арифметическое выражение. Для реализации парсера нам потребуется вспомогательный тип-функция для преобразования строкового литерала в числовой ('5' в 5, например).

type StringToNumber<T extends string, A extends number[] = []> =
    T extends keyof [0, ...A] 
		? A['length'] 
		: StringToNumber<T, [0, ...A]>;

Теперь реализуем парсер:

type StringToCalcExpression<Str extends string> =
		Str extends `${infer L}+${infer R}`
    ? { 
    		left: StringToCalcExpression<L>,
        right: StringToCalcExpression<R>,
        operation: '+' 
      }
    : Str extends `${infer L}-${infer R}`
        ? { 
        		left: StringToCalcExpression<L>,
            right: StringToCalcExpression<R>,
            operation: '-' 
          }
        : Str extends `${infer L}*${infer R}`
            ? { 
            		left: StringToCalcExpression<L>,
                right: StringToCalcExpression<R>,
                operation: '*' 
              }
            : StringToNumber<Str>;

Умножение выполняется в первую очередь, поэтому в дереве оно должно находиться на самом нижнем уровне. Ключевое слово infer позволяет определять внутренние переменные-дженерики "на лету". Таким образом, получается что-то вроде паттерн-мэтчинга: если строка соответствует шаблону L+R, то добавляем очередной узел дерева со сложением, и парсим L и R отдельно. К сожалению, арифметические операции необходимо выписывать вручную, немного дублируя код. Это связано с ограничениями обработки TS-ом строковых выражений.

Обходим дерево и вычисляем резульата

Проходим по дереву снизу вверх и выполняем операции MUL, ADD, SUB в соответствии с указанным символом. Можно было бы в Operation сохранять тип-функцию вместо символа, но в отличие от функций JS, в TS дженерик тип нельзя использовать без аргументов.

type CalcByExpression<Expression extends CalcEpression> = 
		Expression extends CalcExpressionNode
    ? (
        Expression['operation'] extends '*'
            ? Mul<
      					CalcByExpression<Expression['left']>,
								CalcByExpression<Expression['right']>
							>
            : Expression['operation'] extends '-'
                ? Sub<
										CalcByExpression<Expression['left']>, 
										CalcByExpression<Expression['right']>
								>
                : Add<
										CalcByExpression<Expression['left']>, 
										CalcByExpression<Expression['right']>
								>
        )
    : Expression;

Результат

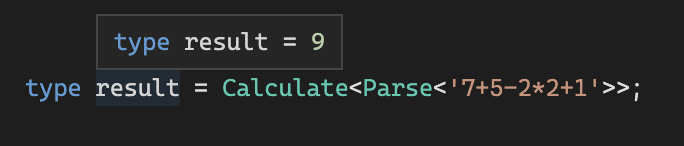
Попробуем вычислить 7+5-2*2+1

type result = CalcByExpression<StringToCalcExpression<'7+5-2*2+1'>>;

Проверяем:

Сделать один тип Calc, не получится: TS будет бояться бесконечной рекурсии :(

По этой же причине нам пришлось проводить вычисления в два этапа: сначала делать дерево, а потом его обходить.

Выводы

Полученная реализация далека от идеала — не хватает поддержки пробелов в строковых выражениях и работы с отрицательными числами. Первое не так страшно, а вот из-за второго некоторые выражения, в процессе вычисления которых получаются отрицательные числа, не будут вычислены. Но обе проблемы достаточно легко решаются с помощью приемов, описанных выше.

Вряд ли вам когда-то понадобится делать что-то подобное в продакшене. Главная идея тут скорее в том, что TypeScript открывает нам огромный простор для точного и строгого описания типов, о котором мы чаще всего забываем, и вместо надежного описания типа явно или неявно используем any, либо unknown с дальнейшим преобразованием. Такой груз накапливается спринтами как бомба замедленного действия, сводя на нет всю пользу TypeScript. Используйте типы с умом!