Процедурная генерация бумажных снежинок

Привет! Скоро начинаются предпраздничные дни, а вместе с ними и украшение наших домов. По этому поводу я решил заняться процедурной генерацией лекала для вырезания из бумаги снежинок, и вот что у меня получилось.

Идея

Изначально мысль о подобном алгоритме пришла ко мне после объявления конкурса на новогоднее приложение в системе Сбер Салют. Я начал думать над идеей того, что бы такого сделать на новогоднюю тематику с управлением голосом, да ещё и чтобы детям нравилось (основная аудитория приложений на голосовых платформах — дети). К тому же, посмотрев много видео о процедурной генерации, давно хотел попробовать придумать что-то своё. Так и решил: пусть по шагам приложение объясняет, как сложить и вырезать снежинку, а сама снежинка каждый раз получается уникальная и неповторимая — прямо как настоящие снежинки за окном!

Теория снежинкосложения

Люди иногда складывают снежинку неправильно: в два раза, а затем снова в два, но в итоге после вырезания получается не слишком аккуратный квадрат.

Есть схема складывания в 8 раз — она сама по себе простая, но резать очень сложно из-за большой толщины. При этом раскрытая снежинка получается хоть и симметричной, однако не столь похожей на настоящую. Так что я остановился на классической, и, пожалуй, самой распространённой схеме с шестью лучами. В ней есть один хитрый шаг: нужно на глаз сложить два конца внахлёст. После небольшой тренировки лично у меня стало получаться без особых проблем. В приложение я вообще добавил возможность прикладывать бумагу к экрану и отмечать нужные линии.

Схема складывания в картинке

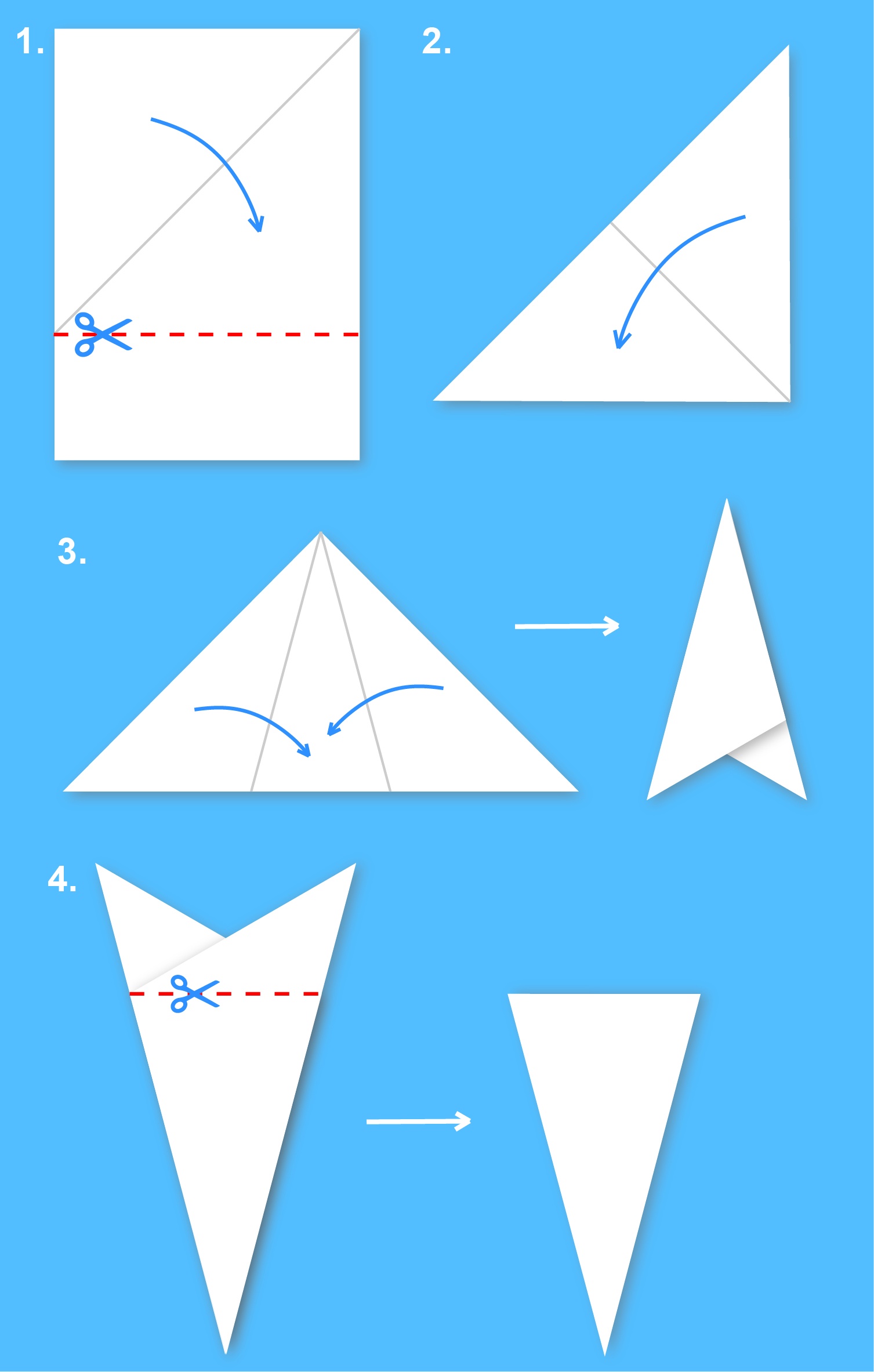
Теория снежинковырезания

После складывания мы получаем равнобедренный треугольник с меньшим углом 30°. Можно было бы вырезать в нём посередине какую-то форму, но это сложно и не даст хорошего результата. Вместо этого будем надрезать по краям. Каждый такой вырез повторится в разложенной снежинке 12 раз: 6 прямым образом и 6 обратным, зеркально.

Поиграться с этим принципом можно, например, в Paper Snowflake Maker. Там изначальная обрезка немного отличается, но привести её к нашей дело двух секунд.

Рассматривая картинки в сети, я вывел для себя один объективный и один субъективный принцип.

• Объективный: нельзя целиком срезать левый или правый край, иначе снежинка развалится на несколько частей.

• Субъективный: получается красиво, если верхняя сторона треугольника содержит сильный перепад высот.

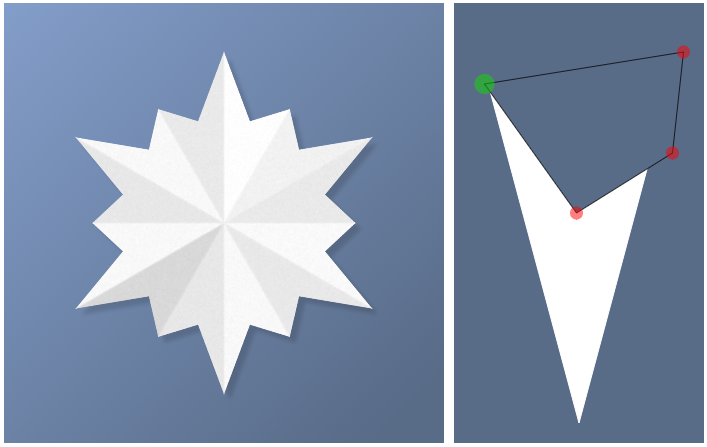
Работа алгоритма

Создавалось веб-приложение с генерацией на фронтенде, так что написано всё на TypeScript, а интерфейс обёрнут во Vue для удобства разработки.

Пара моделей:

export default class Point {
    public x: number;

    public y: number;

    constructor(_x: number, _y: number) {
        this.x = _x;
        this.y = _y;
    }

    public equals(p: Point) {
        return this.x === p.x && this.y === p.y;
    }
}

import Point from './Point';

export default class Segment {
    public start: Point;

    public end: Point;

    constructor(_start: Point, _end: Point) {
        this.start = _start;
        this.end = _end;
    }

    public get xLen(): number {
        return this.end.x - this.start.x;
    }

    public get yLen(): number {
        return this.end.y - this.start.y;
    }

    public get len(): number {
        return Math.sqrt(this.xLen ** 2 + this.yLen ** 2);
    }

    public get ang(): number {
        return Math.atan2(this.end.y - this.start.y, this.end.x - this.start.x);
    }

    public get angDeg(): number {
        return this.ang * (180 / Math.PI);
    }

    public get revAng(): number {
        return Math.atan2(this.start.y - this.end.y, this.start.x - this.end.x);
    }

    public get revAngDeg(): number {
        return this.revAng * (180 / Math.PI);
    }

    public distanceToPoint(p: Point): number {
        const A = p.x - this.start.x;
        const B = p.y - this.start.y;
        const C = this.xLen;
        const D = this.yLen;

        const dot = A * C + B * D;
        const lenSq = C * C + D * D;
        let param = -1;
        if (lenSq !== 0) param = dot / lenSq;

        let xx;
        let yy;

        if (param < 0) {
            xx = this.start.x;
            yy = this.start.y;
        } else if (param > 1) {
            xx = this.end.x;
            yy = this.end.y;
        } else {
            xx = this.start.x + param * C;
            yy = this.start.y + param * D;
        }

        const dx = p.x - xx;
        const dy = p.y - yy;
        return Math.sqrt(dx * dx + dy * dy);
    }
}

Начнём с верхней стороны. Наверное, можно было бы прочертить ломаную методом midpoint displacement, но я решил сделать именно простой внешний контур, который уже потом буду обрабатывать. Поэтому верхняя часть создаётся в двух вариациях. Левый угол остаётся всегда нетронутым, а справа:

Либо выбирается случайная точка во второй сверху четверти правой стороны:

export const getPointFromStart = (segment: Segment, fraction: number): Point => {
    const { xLen, yLen } = segment;
    const xTrim = fraction * xLen;
    const yTrim = fraction * yLen;
    return new Point(segment.start.x + xTrim, segment.start.y + yTrim);
};

// объявлены left: Segment, right: Segment, соответственно,
// левая и правая стороны треугольника;
// возвращается массив отрезков верхней грани

const fullCutMinFraction = 0.25;
const fullCutMaxFraction = 0.5;

const topLastPt = getPointFromStart(right, rand(fullCutMinFraction, fullCutMaxFraction));
return [new Segment(left.end, topLastPt)];

Либо от левого угла откладывается вниз-вправо отрезок, не доходящий до правой стороны, а потом от него ещё один вверх-вправо до пересечения с ней:

export const fromAngAndLen = (start: Point, ang: number, len: number): Segment => {
    const end = new Point(start.x + len * Math.cos(ang), start.y + len * Math.sin(ang));
    return new Segment(start, end);
};

// дополнительно объявлен top: Segment, верхняя сторона треугольника

const maxAng = 45;
const minAng = 15;
const partCutMinLen = 0.3;
const partCutMaxLen = 0.8;

const topFirstAng = left.revAngDeg - rand(minAng, maxAng);
const topFirstLen = top.len * rand(partCutMinLen, partCutMaxLen);
const topFirst = fromAngAndLen(left.end, topFirstAng * toRad, topFirstLen);
const topToIntersect = fromAngAndLen(left.end, topFirstAng * toRad, left.len);
const intPt = intersect(right, topToIntersect) as Point;

const next = new Segment(topFirst.end, randomPointBetween(right.start, intPt));
return [topFirst, next];

Метод intersect это просто обёртка над npm-пакетом line-intersect, проверяющим пересечение двух отрезков. Содержимое тривиальных функций вроде rand приводить не буду, в репозитории есть.

Делаем надрезы

Вручную люди создают очень красивые узоры, иногда вырезают целые сценки со снеговиками и ёлками. Мы так, конечно, не сможем. Точнее, сможем, но число таких рисунков будет конечно, а мы хотим бесконечность снежинок и процедурно. Остановимся на некотором простом паттерне, который будет повторяться с разными значениям случайных величин.

Итак, у нас есть набор отрезков, описывающих внешний контур. Попробовав несколько вариантов, решил делать в этом контуре треугольные вырезы разных размеров. Были ещё тесты с прямоугольными и трапециевидными вырезами, но они чаще всего получались не слишком красивыми после отражения. Что касается круглых и овальных форм: см. в самом конце статьи блок о возможных доработках. Таким образом:

Каждый вырез это треугольник, одна из сторон которого лежит на отрезке всей фигуры, а противоположная этой стороне вершина лежит внутри всей фигуры.

И они должны подчиняться нескольким условиям:

1. Края такого выреза не могут доходить до концов отрезка, в котором вырез совершён. Это позволит нам гарантировать, что мы не срежем целиком левый или правый край всей фигуры.

2. Глубина такого выреза должна быть такой, чтобы он не соединялся с другим вырезом и не пересекал противоположную сторону.

3. Вырез не должен быть слишком маленьким, тогда его будет неудобно делать. Но и не должен быть огромным, чтобы не занять собой всё пространство. О количестве и размере — чуть ниже.

Собственно, задача написать такой алгоритм, который позволит соблюсти все три условия.

Сторона на отрезке фигуры

Начнём с выбора стороны, лежащей на отрезке. У меня она называется edgeSegment. Пусть заданы величины:

let margin: number; // минимально допустимое расстояние от края edgeSegment до одного из концов отрезка
let minEdgeSegmentLen: number; // минимально допустимая длина edgeSegment
let maxEdgeSegmentLen: number; // максимально допустимая длина edgeSegment

Сначала мы выбираем segment: тот отрезок из внешнего контура, в котором начнём что-то вырезать. Очевидно, что выбирать его нужно только из тех отрезков, длина которых не менее margin * 2 + minEdgeSegmentLen, потому что иначе на отрезке не хватит места для выреза. Сам по себе edgeSegment удобнее создавать от его центральной точки centerPoint, выбрав в заданных пределах половину длины и отложив отрезки по обе стороны.

export const getSubSegment = (segment: Segment, margin: number): Segment => {
    const l = segment.len;
    const startEdge = margin / l;
    const endEdge = 1 - startEdge;
    return new Segment(getPointFromStart(segment, startEdge), getPointFromStart(segment, endEdge));
};

export const randomPointWithMargin = (segment: Segment, margin: number): Point => {
    const ss = getSubSegment(segment, margin);
    return randomPointBetween(ss.start, ss.end);
};

// select segment and remove
const segmentIndex = selectSegment(segments);
if (segmentIndex === -1) return null;
const segment = segments[segmentIndex];

// choose center point and sides
const centerPoint = randomPointWithMargin(segment, margin + minEdgeSegmentLen / 2);
const shortestSide = Math.min(dist(centerPoint, segment.start), dist(centerPoint, segment.end));
const halfEdgeSegmentLen = rand(minEdgeSegmentLen / 2,
    Math.min(shortestSide - margin, maxEdgeSegmentLen / 2));

// select angles
const segmentAng = segment.angDeg;

// create side segment
const topHalf = fromAngAndLen(centerPoint, segmentAng * toRad, halfEdgeSegmentLen);
const bottomHalf = fromAngAndLen(centerPoint, (segmentAng + 180) * toRad, halfEdgeSegmentLen);
const edgeSegment = new Segment(bottomHalf.end, topHalf.end);
const fullEdgeSegLen = edgeSegment.len;

Исходный отрезок всей фигуры при этом исключается из массива отрезков, но вместо этого туда помещаются два вновь получившихся кусочка сверху и внизу от красного edgeSegment. Это мы сделаем в конце.

We need to go deeper

Теперь уйдём вглубь. Нам нужно отложить от полученного sideSegment вершину внутрь фигуры. Откладывать будем отрезок от centerPoint для удобства (то есть медиану будущего треугольника). Однако, если все вырезы будут равнобедренными треугольниками, рисунок получится скучный. Поэтому немного рандомизируем, добавив наклон (slant).

const maxSlantAng = 60;

const normal = segmentAng + 90;
const slantAng = rand(normal - maxSlantAng, normal + maxSlantAng);

У нас есть точка, от которой мы откладываем новый отрезок. И есть угол, под которым откладываем. Теперь самое сложное: выбрать глубину выреза (то есть длину медианы, которую мы хотим получить). Помним, что мы не должны пересечь второй раз внешний контур, иначе снежинка развалится на две части.

Применим нечто похожее на ray casting: по всему sideSegment под углом slantAng пустим лучи через некоторый шаг. Как только такой луч пересечётся с любым внешним отрезком, кроме текущего — запомним эту точку. Самая ближайшая точка пересечения и будет нашей максимально допустимой глубиной для выреза.

const shortestDist = (segments: Segment[], proj: Segment) => {
    let minDist = Number.MAX_VALUE;
    segments.forEach((s) => {
        const i = intersect(s, proj);
        if (i !== null) {
            const d = dist(i, proj.start);
            if (d < minDist) {
                minDist = d;
            }
        }
    });

    return minDist;
};

Константу maxProjection считайте просто очень большим числом.

// construct segments list to check intersections
const allSeg = segments.filter((s) => s !== segment);

// maximum length of cutout
// resolution of steps is twice higher than minimum cutout width
const steps = Math.ceil((fullEdgeSegLen * 2) / minEdgeSegmentLen);
const stepSize = fullEdgeSegLen / steps;
let maxLen = Number.MAX_VALUE;

// create projection for every step
for (let i = 0; i <= steps; i++) {
	const startProj = getPointFromStart(edgeSegment, (i * stepSize) / fullEdgeSegLen);
	const proj = fromAngAndLen(startProj, slantAng * toRad, maxProjection);
	const minDist = shortestDist(allSeg, proj);
	if (minDist < maxLen) {
		maxLen = minDist;
	}
}

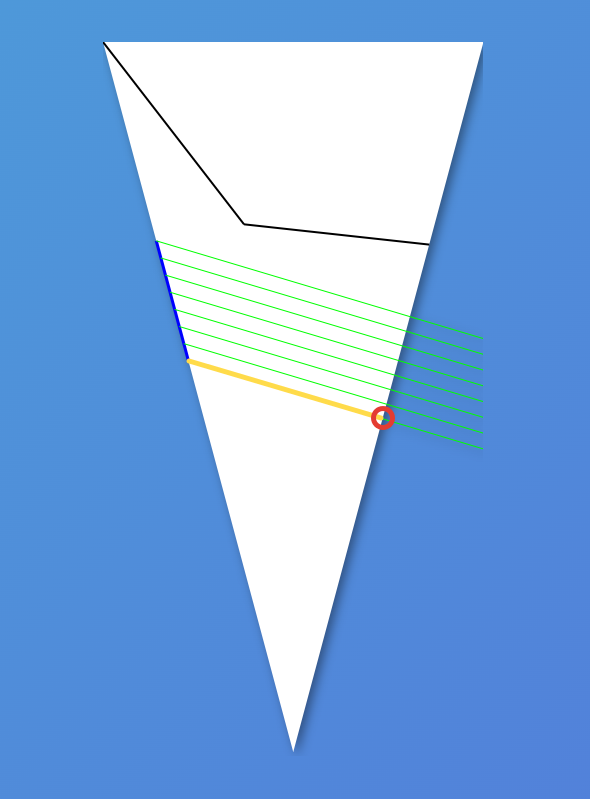
В данном случае нижний луч раньше всех пересёк правую сторону. Длина получившегося при этом отрезка — максимально допустимая глубина выреза. Но, чтобы вырезы не касались края, введём дополнительно отступ:

let innerMargin: number;
maxLen -= innerMargin;

Так что результирующая длина это «чуть не доходя до края».

Окей, это оценка сверху. А что насчёт снизу? Какая минимально возможная глубина выреза, не ноль же?

Введём такие понятия:

1. Минимально допустимая глубина (длина) выреза, просто некоторое число.

2. Допустимые границы площади выреза. То, сколько материала мы уберём из снежинки этим вырезом. Если убрать слишком мало, это почти не окажет интересного эффекта на узор. Если убрать очень много, будет большая дыра — некрасиво. Для скорости здесь как раз все треугольники полагаются равнобедренными, и их площадь считается, как половина произведения медианы на основание.

3. Допустимая растянутость выреза. Отношение его глубины к длине edgeSegment. Если вырез чрезмерно тонкий и длинный, его будет тяжело сделать ножницами.

let minCutoutLength: number;
let minCutoutSq: number;
let maxCutoutSq: number;
let maxCutoutStretch: number;

// if there are no normal intersections skip creating current cutout
if (maxLen > maxProjection) return null;

// truncate length based on maximum square and maximum stretch
maxLen = Math.min(
	maxLen,
	maxCutoutSq / halfEdgeSegmentLen,
	maxCutoutStretch * fullEdgeSegLen,
);
const minLen = Math.max(minCutoutLength, minCutoutSq / halfEdgeSegmentLen);

// edges are too close
if (maxLen < minLen) return null;

Да, здесь появляется return null. К сожалению, я не смог придумать способа, чтобы метод всегда гарантированно создавал валидные вырезы. Знаю, что в процедурной генерации так не очень принято, но на данном этапе просто отбрасываем варианты, которые не прошли проверку. Это отбрасывание пригодится и позже. А пока создаём нужный отрезок и берём его конец в качестве новой вершины.

import Segment from '@/models/Segment';
import Point from '@/models/Point';

export default class Cutout {
    public sideSeg: Segment;

    public firstSeg: Segment;

    public secondSeg: Segment;

    constructor(sideSeg: Segment, firstSeg: Segment, secondSeg: Segment) {
        this.sideSeg = sideSeg;
        this.firstSeg = firstSeg;
        this.secondSeg = secondSeg;
    }

    public get points(): Point[] {
        return [this.sideSeg.start, this.firstSeg.end, this.sideSeg.end, this.sideSeg.start];
    }
}

let cutoutLength: number = rand(minLen, maxLen);
let cutoutMain: Segment = fromAngAndLen(centerPoint, slantAng * toRad, cutoutLength);

const topSegment = new Segment(edgeSegment.end, cutoutMain.end);
const bottomSegment = new Segment(edgeSegment.start, cutoutMain.end);

// cut segment and put new segment parts back
const startSegment = new Segment(segment.start, edgeSegment.start);
const endSegment = new Segment(edgeSegment.end, segment.end);
segments.splice(segmentIndex, 1, startSegment, endSegment);

// return
const cutout = new Cutout(edgeSegment, topSegment, bottomSegment);
cutouts.push(cutout);
return cutout;

Чтобы новый вырез не пересекался не только с внешними границами рисунка, но и со старыми вырезами, просто добавим все стороны старых вырезов к списку отрезков, на которых мы проверяем пересечение.

// construct segments list to check intersections
const allSeg = segments.filter((s) => s !== segment)
    .concat(cutouts.map(((c) => [c.firstSeg, c.secondSeg])).flat());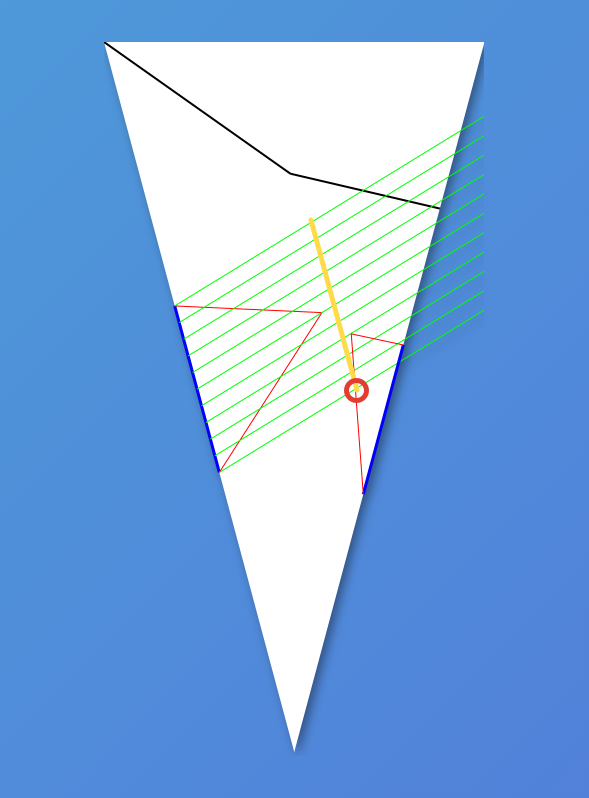

Конечно, можно было бы учесть геометрию вырезов, и для крайних лучей сделать иную оценку пересечений, нежели для средних. Но пара приблизительных тестов показала, что результат не стоит усилий.

Для ускорения работы я добавил взвешенный выбор изначального отрезка: более длинные берутся с большей вероятностью.

const selectSegment = (segments: Segment[]) => {
    const suitableSegments = segments.filter((s) => s.len >= margin * 2 + minEdgeSegmentLen);
    if (suitableSegments.length === 0) return -1;

    // select segments based on its length
    const sumLength = suitableSegments.reduce((sum, { len }) => sum + len, 0);
    const r = rand(0, sumLength);
    let currentLength = 0;
    for (let i = 0; i < suitableSegments.length; i++) {
        currentLength += suitableSegments[i].len;
        if (r <= currentLength) return segments.indexOf(suitableSegments[i]);
    }

    return -1;
};

Повторяем операцию вырезания до тех пор, пока много раз не получим от системы информацию о невозможности создать новый вырез (метод вернёт null).

let maximumIterations: number;

// generate cutouts
let iterations = maximumIterations;
while (iterations-- > 0 && segments.length > 0) {
	const cutout = generateCutout(segments, cutouts);
	if (cutout !== null) {
		iterations = maximumIterations;
	}
}

Я остановился на maximumIterations = 5000, эта цифра давала хороший результат и не приводила к тормозам даже на слабых устройствах.

Исправляем косяки и делаем твики

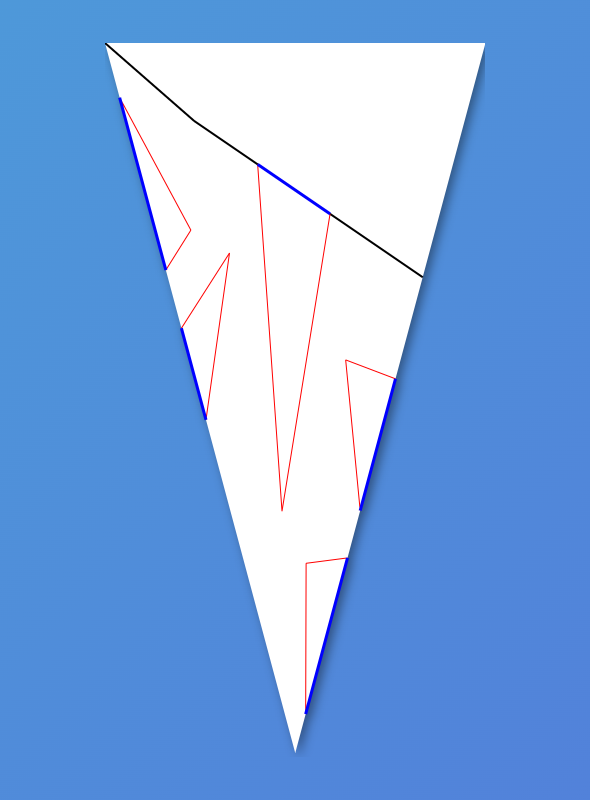
К сожалению, практика показала, что вычисление допустимой глубины с помощью лучей иногда даёт сбой. Например, вырез может быть очень тонким, и лучи пролетают мимо него. Вот на примере ниже я дорисовал вероятные лучи сам (вывод лучей программой был отключён), и видно, что даже самый короткий из них всё-таки недостаточно короткий.

Можно было бы уменьшить шаг, через который чертятся лучи, но это показалось мне не слишком надёжным. Кстати, обратите внимание, что уменьшение шага вдвое на примере выше не помогло бы. Поэтому после построения треугольника я добавил две проверки:

1. Расстояние от новой вершины до всех старых отрезков (отрезки внешней фигуры + отрезки предыдущих вырезов).

2. Расстояние от двух новых сторон до всех предыдущих вершин (вершин вырезов + вершин внешней фигуры).

let pointToSegmentMargin: number;

// generate length and segments
let pointDistanceCheck = false;
let cutoutLength: number = rand(minLen, maxLen);
let cutoutMain: Segment = fromAngAndLen(centerPoint, slantAng * toRad, cutoutLength);
let topSegment: Segment | null = null;
let bottomSegment: Segment | null = null;

while (!pointDistanceCheck) {
    if (cutoutLength < minLen) return null;

    // check new point for distance with segments
    const mainPoint = cutoutMain.end;
    const minDistPS = shortestDistBetweenPointAndSegments(allSeg, mainPoint);
    if (minDistPS < pointToSegmentMargin) {
        cutoutLength -= pointToSegmentMargin;
        cutoutMain = fromAngAndLen(centerPoint, slantAng * toRad, cutoutLength);
    } else {
        // check new segments for distance with points
        const allPoints = segments
            .filter((s) => s !== segment)
            .map((s) => [s.start, s.end])
            .flat()
            .concat(cutouts.map((c) => c.firstSeg.end));

        // create segments to check
        topSegment = new Segment(edgeSegment.end, cutoutMain.end);
        bottomSegment = new Segment(edgeSegment.start, cutoutMain.end);
        const minDistSP = Math.min(
            shortestDistBetweenPointsAndSegment(topSegment, allPoints),
            shortestDistBetweenPointsAndSegment(bottomSegment, allPoints),
        );

        if (minDistSP < pointToSegmentMargin) {
            cutoutLength -= pointToSegmentMargin;
            cutoutMain = fromAngAndLen(centerPoint, slantAng * toRad, cutoutLength);
        } else {
            pointDistanceCheck = true;
        }
    }
}

topSegment = topSegment || new Segment(edgeSegment.end, cutoutMain.end);
bottomSegment = bottomSegment || new Segment(edgeSegment.start, cutoutMain.end);

Дёшево и сердито, это полностью решило проблему.

Настройка генерации

Как видите, генерацией управляет около десятка констант: допустимые длины, площади, углы, whatever. Не хотелось каждый раз подбирать эти числа, поэтому было решено задавать их все одной величиной: cutoutRatio. Чем больше cutoutRatio, тем более мелкие вырезы создаются, и, следовательно, тем больше их количество. В среднем подобрано так, чтобы cutoutRatio < 1 генерировал совсем примитивные снежинки для детей, а cutoutRatio > 5 был фактически абсурдным и нереалистичным.

export const initCutoutGen = (cutoutsRatio: number, w: number, longest: number): void => {
    const sqRatio = cutoutsRatio ** 0.5;
    const quarterRatio = cutoutsRatio ** 0.25;
    margin = (w * 0.08) / sqRatio;
    innerMargin = (margin * 2) / quarterRatio;
    pointToSegmentMargin = margin / quarterRatio;
    minEdgeSegmentLen = (w * 0.1) / cutoutsRatio;
    maxEdgeSegmentLen = (w * 0.5) / Math.max(1, quarterRatio);
    minCutoutSq = (w * w * 0.04) / cutoutsRatio;
    maxCutoutSq = (w * w * 0.10) / Math.max(1, quarterRatio);
    maxProjection = longest * 2;
    minCutoutLength = minEdgeSegmentLen / 2;
    maxCutoutStretch = 5 * Math.max(1, cutoutsRatio);
};

Здесь w это ширина верхней стороны треугольника: я решил всё задавать относительно неё. А longest это длина самой большой высоты в треугольнике, чтобы по ней понять, какие нужно делать проекции для пересечения.

А теперь будет магия

Нам остаётся визуально стереть все очерченные фигуры из основы. Сделать это можно, например, с помощью globalCompositeOperation = 'destination-out', но я не буду подробно касаться данной темы. Кому интересно, в репозитории весь код, в том числе для приложения под Салют.

Обрезав треугольник, его нужно скопировать на другой канвас шесть раз по часовой стрелке, и шесть раз против часовой, отразив зеркально. Код такого рисования не представляет интереса в рамках данной статьи, но приведу его для порядка. Я добавил туда немного украшательств виде разной степени яркости на снежинке, будто бы она сложена из бумаги. Это привело к появлению громоздкого костыля для Safari, но тут уже другая история.

import { toRad } from '@/engine/utils';

// just dont ask...
const createCanvasFiltered = (ctx: CanvasRenderingContext2D, amount: number): HTMLCanvasElement => {
    // get source data
    const { height, width } = ctx.canvas;
    const imageData = ctx.getImageData(0, 0, width, height);
    const { data } = imageData;

    // change brightness
    for (let i = 0; i < data.length; i += 4) {
        data[i] = Math.floor(data[i] * amount);
        data[i + 1] = Math.floor(data[i + 1] * amount);
        data[i + 2] = Math.floor(data[i + 2] * amount);
    }

    // create fake canvas
    const canvas = document.createElement('canvas');
    canvas.width = width;
    canvas.height = height;

    // fill context
    const context = <CanvasRenderingContext2D>canvas.getContext('2d');
    context.putImageData(imageData, 0, 0);
    return canvas;
};

export default function generateFullSnowflake(): void {
    const canvasSrc = <HTMLCanvasElement>document.getElementById('canvas');
    const canvasFinal = <HTMLCanvasElement>document.getElementById('cFinal');
    const ctxSrc = <CanvasRenderingContext2D>canvasSrc.getContext('2d');
    const ctx = <CanvasRenderingContext2D>canvasFinal.getContext('2d');
    ctx.resetTransform();
    ctx.clearRect(0, 0, canvasFinal.width, canvasFinal.height);
    const w = canvasSrc.width;
    const h = canvasSrc.height;
    const longestSide = Math.sqrt((w / 2) ** 2 + h ** 2);
    const scale = canvasFinal.width / (longestSide * 2);

    ctx.scale(scale, scale);
    ctx.translate(canvasFinal.width / (2 * scale), canvasFinal.height / (2 * scale));

    // Okay, there is a workaround for fucking Safari, again. Safari cannot use ctx.filter
    // and also it updates context for only last operation, so we should create a new
    // canvas element for each desired brightness.
    // Yes, it is awful, but people for some reason still use iPhones and other Apple devices.
    const brightnesses: string[] = ['100', '97', '93', '100', '97', '100', '97', '90', '97', '93', '97', '93'];
    const canvases: { [key: string]: HTMLCanvasElement; } = {};
    brightnesses.forEach((b) => {
        if (!canvases[b]) {
            canvases[b] = createCanvasFiltered(ctxSrc, Number.parseInt(b, 10) / 100);
        }
    });

    // clockwise parts
    ctx.rotate(-45 * toRad);
    for (let i = 0; i < 6; i++) {
        // ctx.filter = `brightness(${(brightnesses[i * 2])}%)`; // doesnt work in Safari
        const filteredCanvas = canvases[brightnesses[i * 2]];
        ctx.rotate(60 * toRad);
        ctx.drawImage(filteredCanvas, -w / 2, -h);
    }

    // counter clockwise parts
    ctx.scale(-1, 1);
    ctx.rotate(-90 * toRad);
    for (let i = 0; i < 6; i++) {
        // ctx.filter = `brightness(${(brightnesses[11 - i * 2])}%)`; // doesnt work in Safari
        const filteredCanvas = canvases[brightnesses[11 - i * 2]];
        ctx.rotate(60 * toRad);
        ctx.drawImage(filteredCanvas, -w / 2, -h);
    }
}

Получается что-то такое. Здесь, как видно, cutoutRatio = 1.7

Вообще, симметрия добавляет гармонии даже там, где изначально, казалось бы, есть только что-то невнятное. По рисунку слева никогда не скажешь, что из этого может получиться что-то красивое. Но лично мне результат нравится.

Примеры

Ещё несколько вариантов по мере увеличения cutoutRatio (слева направо сверху вниз).

В приложение для Салюта я добавил пошаговую визуально-голосовую инструкцию.

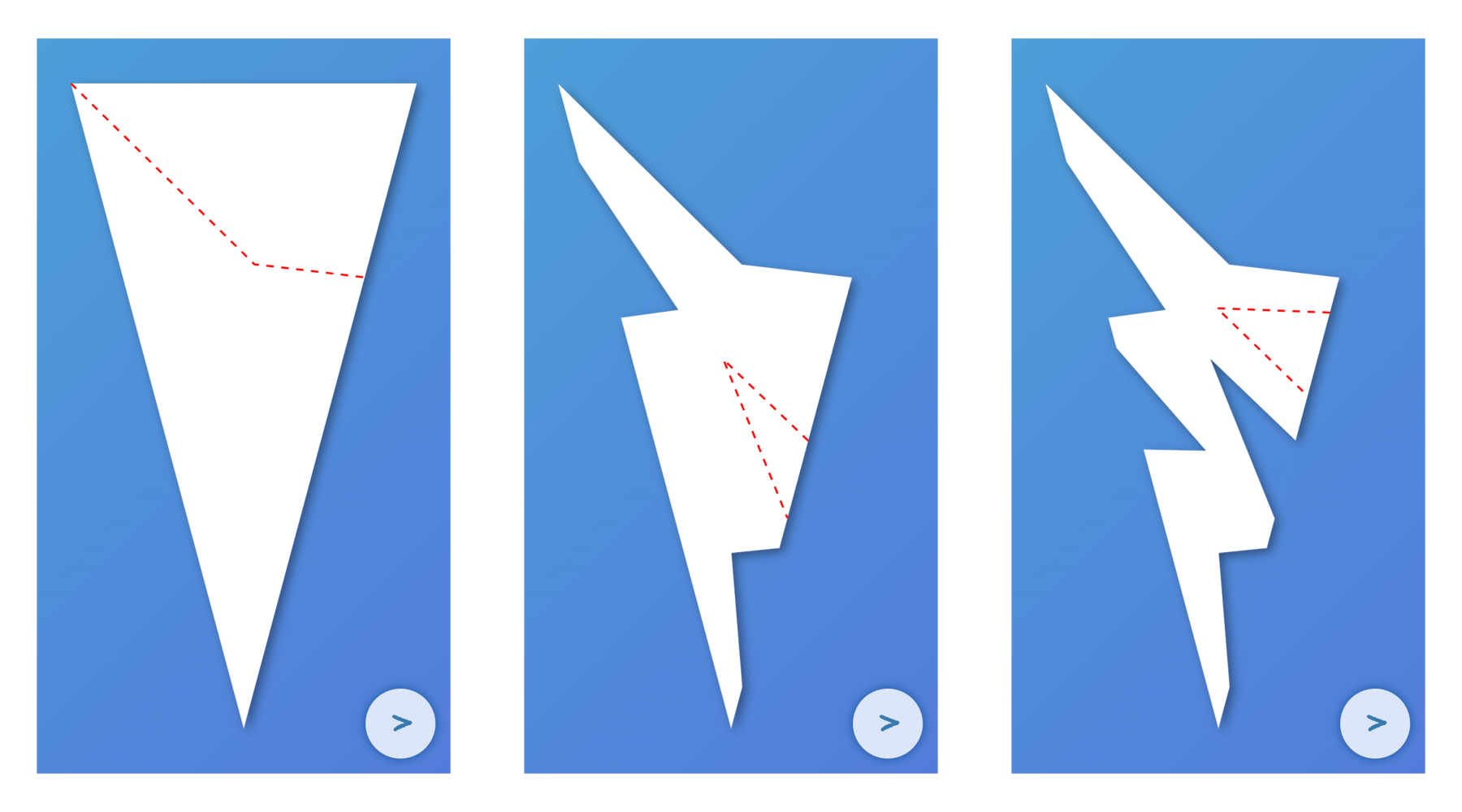
В онлайн-демке есть возможность сгенерировать PDF для последующей печати и вырезания. Там раскрашены области, которые нужно отрезать, главное сложить этими областями наружу.

Тест-драйв в реальных условиях

Здесь cutoutRatio = 1.7. Кажется, получилось неплохо.

Что можно добавить или улучшить

• Понятно, что алгоритм поиска глубины выреза можно улучшать бесконечно.

• Можно добавить seed. Джаваскрипт из коробки (как я понял) так не умеет, придётся переписывать всё на внешнюю библиотеку вроде Вихря Мерсенна, и как-то обрабатывать ситуацию, когда заданный seed не выдаёт вообще никакого приемлемого набора вырезов.

• Круги и овалы — была мысль случайным образом менять некоторые отрезки на дуги большого радиуса, но воплотить уже времени не хватило.

• Центр снежинки (нижний уголок треугольника) тоже можно как-то красиво обрезать.

Присылайте пулл-реквесты!

Ссылки

• Приложение в системе Салют.

• Онлайн-демка с возможностью сгенерировать PDF.

• Репозиторий приложения.

• Ветка с кодом онлайн-демки (пулл-реквесты делать сюда).