 There is no difference between theory and practice in theory,
There is no difference between theory and practice in theory, but there is often a great deal of difference between theory
and practice in practice.
Я слепым вместо глаз вставил звезды и синее небо.
Юрий Шевчук
Тема игровых ботов с самого начала была для меня довольно чувствительной. Используя Dagaz, я научился воссоздавать самые разнообразные игры, но что в них толку, если с тобой никто не играет? Nest позволил разработать сервер, для игры по сети, но до тех пор пока на нём не слишком много народу, боты продолжают оставаться актуальными. Универсальные боты, которые я писал, были медленными и слабыми. К счастью, знакомство с Garbochess позволило переломить ситуацию, по крайней мере в том, что касалось шахматных игр. Признаюсь честно, я никогда не думал, что у меня появится бот для игры в Го…
до тех пор, пока не прочитал эту книгу:

Дело в том, что с точки зрения AI, игра Го, по многим причинам, считается одной из самых сложных настольных игр. Разумеется, боты для этой игры разрабатывались и ранее, но их сила не превышала 2-3 дан, что по меркам игрового сообщества является довольно средним показателем. Возможность разработки для Го сильного бота всерьёз не рассматривалась, вплоть до триумфальной победы Alpha Go в марте 2016 года. В своей книге, Макс Памперла и Кевин Фергюсон, подробно и двигаясь от простого к сложному, объясняют, как это стало возможно и каким образом устроены как Alpha Go, так и результат дальнейшего развития этого проекта — AlphaGo Zero.
А внутре у ей нейронка!
Разумеется, дело не обошлось без нейросетей. Тактика игры Го основана на построении "хороших форм", позволяющих захватить большую территорию, защитив её оптимальным образом. Оценка позиции, таким образом, сводится к оценке форм — образов, возникающих на доске в процессе игры. Нейросети, в особенности свёрточные, и методы глубокого обучения, со своей стороны, хорошо зарекомендовали себя в задачах распознавания образов. Было вполне логично попытаться применить одно к другому. Результат оказался неожиданным, хотя и выглядит довольно закономерным, в ретроспективе.
Помимо книги, авторы предоставили доступ к исходным кодам в GitHub-репозитории. Конечно же, для разработки использовался Python, ставший фактическим стандартом в приложениях машинного обучения. Также, в проекте были использованы библиотеки Tensorflow и Keras.
valentin@ecomdev2:/opt/go$ source venv/bin/activate
(venv) valentin@ecomdev2:/opt/go$ pip3 install -r requirements.txt
...
ERROR: dlgo 0.2 has requirement keras==2.2.2, but you'll have keras 2.6.0 which is incompatible.
ERROR: dlgo 0.2 has requirement numpy<=1.14.5, but you'll have numpy 1.21.2 which is incompatible.
ERROR: tensorflow 2.6.0 has requirement numpy~=1.19.2, but you'll have numpy 1.21.2 which is incompatible.
...
(venv) valentin@ecomdev2:/opt/go$ pip3 install tensorflow==2.2.2
...
ERROR: keras 2.2.2 has requirement keras-preprocessing==1.0.2, but you'll have keras-preprocessing 1.1.2 which is incompatible.
ERROR: dlgo 0.2 has requirement numpy<=1.14.5, but you'll have numpy 1.18.5 which is incompatible.
...
(venv) valentin@ecomdev2:/opt/go$ pip3 install keras-preprocessing==1.0.2
...
ERROR: tensorflow 2.2.2 has requirement keras-preprocessing>=1.1.0, but you'll have keras-preprocessing 1.0.2 which is incompatible.
ERROR: dlgo 0.2 has requirement numpy<=1.14.5, but you'll have numpy 1.18.5 which is incompatible.
...
(venv) valentin@ecomdev2:/opt/go$ pip3 install "keras-preprocessing>=1.1.0"
...
ERROR: keras 2.2.2 has requirement keras-preprocessing==1.0.2, but you'll have keras-preprocessing 1.1.2 which is incompatible.
ERROR: dlgo 0.2 has requirement numpy<=1.14.5, but you'll have numpy 1.18.5 which is incompatible.
...
(venv) valentin@ecomdev2:/opt/go/code$ pip3 install "keras==2.2.2"
...
ERROR: tensorflow 2.2.2 has requirement keras-preprocessing>=1.1.0, but you'll have keras-preprocessing 1.0.2 which is incompatible.
ERROR: tensorflow 2.2.2 has requirement numpy<1.19.0,>=1.16.0, but you'll have numpy 1.14.5 which is incompatible.
ERROR: scipy 1.7.1 has requirement numpy<1.23.0,>=1.16.5, but you'll have numpy 1.14.5 which is incompatible.
...
(venv) valentin@ecomdev2:/opt/go/code$ pip3 install "numpy<1.23.0,>=1.16.5"
...
ERROR: tensorflow 2.2.2 has requirement keras-preprocessing>=1.1.0, but you'll have keras-preprocessing 1.0.2 which is incompatible.
ERROR: tensorflow 2.2.2 has requirement numpy<1.19.0,>=1.16.0, but you'll have numpy 1.21.2 which is incompatible.
ERROR: dlgo 0.2 has requirement numpy<=1.14.5, but you'll have numpy 1.21.2 which is incompatible.
...
Вероятно, если бы я строил весь проект, со всеми его зависимостями, с нуля, я смог бы разобраться с этой головоломкой, но добиться работоспособности проекта скачанного с GitHub-а мне так и не удалось. К счастью, этого и не требовалось.
В седьмой главе книги, авторы провели обучение с учителем, взяв за основу данные 100 игр с сервера KGS — международной игровой площадки для игры в Го. Записи ведутся в формате SGF, начиная с 2001 года и содержат только те партии, в которых один из игроков имел 7-ой дан и выше или оба игрока имели 6-ой дан. Результат обучения можно посмотреть по следующей ссылке:

Следует отметить, что игра бота выглядит вполне разумно. Результаты обучения модели, по завершении 5 эпох, можно загрузить с GitHub-а и сконвертировать, при помощи tensorflowjs_converter-а.
$ tensorflowjs_converter --input_format=keras small_model_epoch_5.h5 small_model_epoch_5
{
"format":"graph-model",
"generatedBy":"2.6.0",
"convertedBy":"TensorFlow.js Converter v3.9.0",
"signature":{
"inputs":{
"zero_padding2d_1_input":{
"name":"zero_padding2d_1_input:0",
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"-1"
},
{
"size":"1"
},
{
"size":"19"
},
{
"size":"19"
}
]
}
}
},
"outputs":{
"dense_2":{
"name":"Identity:0",
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"-1"
},
{
"size":"361"
}
]
}
}
}
},
"modelTopology":{
"node":[
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_1/Pad/paddings",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_INT32"
},
"value":{
"tensor":{
"dtype":"DT_INT32",
"tensorShape":{
"dim":[
{
"size":"4"
},
{
"size":"2"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_1/Conv2D/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"7"
},
{
"size":"7"
},
{
"size":"1"
},
{
"size":"48"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_1/BiasAdd/ReadVariableOp",
"op":"Const",
"attr":{
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"48"
}
]
}
}
},
"dtype":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_2/Pad/paddings",
"op":"Const",
"attr":{
"value":{
"tensor":{
"dtype":"DT_INT32",
"tensorShape":{
"dim":[
{
"size":"4"
},
{
"size":"2"
}
]
}
}
},
"dtype":{
"type":"DT_INT32"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_2/Conv2D/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"5"
},
{
"size":"5"
},
{
"size":"48"
},
{
"size":"32"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_2/BiasAdd/ReadVariableOp",
"op":"Const",
"attr":{
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"32"
}
]
}
}
},
"dtype":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_3/Pad/paddings",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_INT32"
},
"value":{
"tensor":{
"dtype":"DT_INT32",
"tensorShape":{
"dim":[
{
"size":"4"
},
{
"size":"2"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_3/Conv2D/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"5"
},
{
"size":"5"
},
{
"size":"32"
},
{
"size":"32"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_3/BiasAdd/ReadVariableOp",
"op":"Const",
"attr":{
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"32"
}
]
}
}
},
"dtype":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_4/Pad/paddings",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_INT32"
},
"value":{
"tensor":{
"dtype":"DT_INT32",
"tensorShape":{
"dim":[
{
"size":"4"
},
{
"size":"2"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_4/Conv2D/ReadVariableOp",
"op":"Const",
"attr":{
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"5"
},
{
"size":"5"
},
{
"size":"32"
},
{
"size":"32"
}
]
}
}
},
"dtype":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_4/BiasAdd/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"32"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/flatten_1/Const",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_INT32"
},
"value":{
"tensor":{
"dtype":"DT_INT32",
"tensorShape":{
"dim":[
{
"size":"2"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/dense_1/MatMul/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"11552"
},
{
"size":"512"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/dense_1/BiasAdd/ReadVariableOp",
"op":"Const",
"attr":{
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"512"
}
]
}
}
},
"dtype":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/dense_2/MatMul/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"512"
},
{
"size":"361"
}
]
}
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/dense_2/BiasAdd/ReadVariableOp",
"op":"Const",
"attr":{
"dtype":{
"type":"DT_FLOAT"
},
"value":{
"tensor":{
"dtype":"DT_FLOAT",
"tensorShape":{
"dim":[
{
"size":"361"
}
]
}
}
}
}
},
{
"name":"zero_padding2d_1_input",
"op":"Placeholder",
"attr":{
"shape":{
"shape":{
"dim":[
{
"size":"-1"
},
{
"size":"1"
},
{
"size":"19"
},
{
"size":"19"
}
]
}
},
"dtype":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_1/Pad",
"op":"Pad",
"input":[
"zero_padding2d_1_input",
"StatefulPartitionedCall/sequential/zero_padding2d_1/Pad/paddings"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"Tpaddings":{
"type":"DT_INT32"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_1/Conv2D",
"op":"Conv2D",
"input":[
"StatefulPartitionedCall/sequential/zero_padding2d_1/Pad",
"StatefulPartitionedCall/sequential/conv2d_1/Conv2D/ReadVariableOp"
],
"device":"/device:CPU:0",
"attr":{
"strides":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"T":{
"type":"DT_FLOAT"
},
"dilations":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"padding":{
"s":"VkFMSUQ="
},
"use_cudnn_on_gpu":{
"b":true
},
"data_format":{
"s":"TkNIVw=="
},
"explicit_paddings":{
"list":{
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_1/BiasAdd",
"op":"BiasAdd",
"input":[
"StatefulPartitionedCall/sequential/conv2d_1/Conv2D",
"StatefulPartitionedCall/sequential/conv2d_1/BiasAdd/ReadVariableOp"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"data_format":{
"s":"TkNIVw=="
}
}
},
{
"name":"StatefulPartitionedCall/sequential/activation_1/Relu",
"op":"Relu",
"input":[
"StatefulPartitionedCall/sequential/conv2d_1/BiasAdd"
],
"attr":{
"T":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_2/Pad",
"op":"Pad",
"input":[
"StatefulPartitionedCall/sequential/activation_1/Relu",
"StatefulPartitionedCall/sequential/zero_padding2d_2/Pad/paddings"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"Tpaddings":{
"type":"DT_INT32"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_2/Conv2D",
"op":"Conv2D",
"input":[
"StatefulPartitionedCall/sequential/zero_padding2d_2/Pad",
"StatefulPartitionedCall/sequential/conv2d_2/Conv2D/ReadVariableOp"
],
"device":"/device:CPU:0",
"attr":{
"use_cudnn_on_gpu":{
"b":true
},
"data_format":{
"s":"TkNIVw=="
},
"padding":{
"s":"VkFMSUQ="
},
"T":{
"type":"DT_FLOAT"
},
"explicit_paddings":{
"list":{
}
},
"dilations":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"strides":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_2/BiasAdd",
"op":"BiasAdd",
"input":[
"StatefulPartitionedCall/sequential/conv2d_2/Conv2D",
"StatefulPartitionedCall/sequential/conv2d_2/BiasAdd/ReadVariableOp"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"data_format":{
"s":"TkNIVw=="
}
}
},
{
"name":"StatefulPartitionedCall/sequential/activation_2/Relu",
"op":"Relu",
"input":[
"StatefulPartitionedCall/sequential/conv2d_2/BiasAdd"
],
"attr":{
"T":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_3/Pad",
"op":"Pad",
"input":[
"StatefulPartitionedCall/sequential/activation_2/Relu",
"StatefulPartitionedCall/sequential/zero_padding2d_3/Pad/paddings"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"Tpaddings":{
"type":"DT_INT32"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_3/Conv2D",
"op":"Conv2D",
"input":[
"StatefulPartitionedCall/sequential/zero_padding2d_3/Pad",
"StatefulPartitionedCall/sequential/conv2d_3/Conv2D/ReadVariableOp"
],
"device":"/device:CPU:0",
"attr":{
"dilations":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"use_cudnn_on_gpu":{
"b":true
},
"padding":{
"s":"VkFMSUQ="
},
"strides":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"explicit_paddings":{
"list":{
}
},
"T":{
"type":"DT_FLOAT"
},
"data_format":{
"s":"TkNIVw=="
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_3/BiasAdd",
"op":"BiasAdd",
"input":[
"StatefulPartitionedCall/sequential/conv2d_3/Conv2D",
"StatefulPartitionedCall/sequential/conv2d_3/BiasAdd/ReadVariableOp"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"data_format":{
"s":"TkNIVw=="
}
}
},
{
"name":"StatefulPartitionedCall/sequential/activation_3/Relu",
"op":"Relu",
"input":[
"StatefulPartitionedCall/sequential/conv2d_3/BiasAdd"
],
"attr":{
"T":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_4/Pad",
"op":"Pad",
"input":[
"StatefulPartitionedCall/sequential/activation_3/Relu",
"StatefulPartitionedCall/sequential/zero_padding2d_4/Pad/paddings"
],
"attr":{
"Tpaddings":{
"type":"DT_INT32"
},
"T":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_4/Conv2D",
"op":"Conv2D",
"input":[
"StatefulPartitionedCall/sequential/zero_padding2d_4/Pad",
"StatefulPartitionedCall/sequential/conv2d_4/Conv2D/ReadVariableOp"
],
"device":"/device:CPU:0",
"attr":{
"padding":{
"s":"VkFMSUQ="
},
"dilations":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"T":{
"type":"DT_FLOAT"
},
"data_format":{
"s":"TkNIVw=="
},
"explicit_paddings":{
"list":{
}
},
"strides":{
"list":{
"i":[
"1",
"1",
"1",
"1"
]
}
},
"use_cudnn_on_gpu":{
"b":true
}
}
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_4/BiasAdd",
"op":"BiasAdd",
"input":[
"StatefulPartitionedCall/sequential/conv2d_4/Conv2D",
"StatefulPartitionedCall/sequential/conv2d_4/BiasAdd/ReadVariableOp"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"data_format":{
"s":"TkNIVw=="
}
}
},
{
"name":"StatefulPartitionedCall/sequential/activation_4/Relu",
"op":"Relu",
"input":[
"StatefulPartitionedCall/sequential/conv2d_4/BiasAdd"
],
"attr":{
"T":{
"type":"DT_FLOAT"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/flatten_1/Reshape",
"op":"Reshape",
"input":[
"StatefulPartitionedCall/sequential/activation_4/Relu",
"StatefulPartitionedCall/sequential/flatten_1/Const"
],
"attr":{
"T":{
"type":"DT_FLOAT"
},
"Tshape":{
"type":"DT_INT32"
}
}
},
{
"name":"StatefulPartitionedCall/sequential/activation_5/Relu",
"op":"_FusedMatMul",
"input":[
"StatefulPartitionedCall/sequential/flatten_1/Reshape",
"StatefulPartitionedCall/sequential/dense_1/MatMul/ReadVariableOp",
"StatefulPartitionedCall/sequential/dense_1/BiasAdd/ReadVariableOp"
],
"device":"/device:CPU:0",
"attr":{
"num_args":{
"i":"1"
},
"T":{
"type":"DT_FLOAT"
},
"fused_ops":{
"list":{
"s":[
"Qmlhc0FkZA==",
"UmVsdQ=="
]
}
},
"transpose_a":{
"b":false
},
"epsilon":{
"f":0.0
},
"transpose_b":{
"b":false
}
}
},
{
"name":"StatefulPartitionedCall/sequential/dense_2/BiasAdd",
"op":"_FusedMatMul",
"input":[
"StatefulPartitionedCall/sequential/activation_5/Relu",
"StatefulPartitionedCall/sequential/dense_2/MatMul/ReadVariableOp",
"StatefulPartitionedCall/sequential/dense_2/BiasAdd/ReadVariableOp"
],
"device":"/device:CPU:0",
"attr":{
"epsilon":{
"f":0.0
},
"num_args":{
"i":"1"
},
"T":{
"type":"DT_FLOAT"
},
"transpose_a":{
"b":false
},
"transpose_b":{
"b":false
},
"fused_ops":{
"list":{
"s":[
"Qmlhc0FkZA=="
]
}
}
}
},
{
"name":"StatefulPartitionedCall/sequential/dense_2/Softmax",
"op":"Softmax",
"input":[
"StatefulPartitionedCall/sequential/dense_2/BiasAdd"
],
"attr":{
"T":{
"type":"DT_FLOAT"
}
}
},
{
"name":"Identity",
"op":"Identity",
"input":[
"StatefulPartitionedCall/sequential/dense_2/Softmax"
],
"attr":{
"T":{
"type":"DT_FLOAT"
}
}
}
],
"library":{
},
"versions":{
"producer":808
}
},
"weightsManifest":[
{
"paths":[
"group1-shard1of6.bin",
"group1-shard2of6.bin",
"group1-shard3of6.bin",
"group1-shard4of6.bin",
"group1-shard5of6.bin",
"group1-shard6of6.bin"
],
"weights":[
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_1/Pad/paddings",
"shape":[
4,
2
],
"dtype":"int32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_1/Conv2D/ReadVariableOp",
"shape":[
7,
7,
1,
48
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_1/BiasAdd/ReadVariableOp",
"shape":[
48
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_2/Pad/paddings",
"shape":[
4,
2
],
"dtype":"int32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_2/Conv2D/ReadVariableOp",
"shape":[
5,
5,
48,
32
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_2/BiasAdd/ReadVariableOp",
"shape":[
32
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_3/Pad/paddings",
"shape":[
4,
2
],
"dtype":"int32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_3/Conv2D/ReadVariableOp",
"shape":[
5,
5,
32,
32
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_3/BiasAdd/ReadVariableOp",
"shape":[
32
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/zero_padding2d_4/Pad/paddings",
"shape":[
4,
2
],
"dtype":"int32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_4/Conv2D/ReadVariableOp",
"shape":[
5,
5,
32,
32
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/conv2d_4/BiasAdd/ReadVariableOp",
"shape":[
32
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/flatten_1/Const",
"shape":[
2
],
"dtype":"int32"
},
{
"name":"StatefulPartitionedCall/sequential/dense_1/MatMul/ReadVariableOp",
"shape":[
11552,
512
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/dense_1/BiasAdd/ReadVariableOp",
"shape":[
512
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/dense_2/MatMul/ReadVariableOp",
"shape":[
512,
361
],
"dtype":"float32"
},
{
"name":"StatefulPartitionedCall/sequential/dense_2/BiasAdd/ReadVariableOp",
"shape":[
361
],
"dtype":"float32"
}
]
}
]
}Самое главное, что, начиная с этого момента, с нейросетью можно работать уже в TensorFlow.js, в браузере, либо, с недавнего времени, и в Node.js.
const tf = require('@tensorflow/tfjs');
model = await tf.loadLayersModel('https://games.dtco.ru/model/model.json');
board = new Float32Array(19 * 19);
const shape = [1, 1, 19, 19];
const d = tf.tensor4d(board, shape, 'float32');
const p = await model.predict(d);
const x = await p.data();
d.dispose();
p.dispose();
Здесь, как человек неопытный, я некоторое время потупил с размерностью тензора с входными данными, пока не понял, что можно передавать по нескольку досок за раз. Вторая по счёту единичка — это количество слоёв входных данных. Об этом я ещё скажу позже, пока что же, модель использует однослойное кодирование: свои камни на доске кодируются 1, камни противника -1, а пустые пункты 0. На выходе получаем массив из 361 элемента (слева-направо и сверху-вниз по доске), содержащие вероятности того, что следующий ход будет выполнен именно в этот пункт.
const URL = 'https://games.dtco.ru/model/model.json';
const tf = require('@tensorflow/tfjs');
const wasm = require('@tensorflow/tfjs-backend-wasm');
await tf.enableProdMode();
await tf.setBackend('wasm');
model = await tf.loadLayersModel(URL);
console.log(tf.getBackend());
и экспериментального флага --experimental-worker в package.json. По хорошему, этот вопрос следовало решать обновлением версии Node.js, но на сервере, на этот момент, уже много чего крутилось и не хотелось предпринимать эксперименты, связанные с его возможным падением. Сразу скажу, что переход на бакенд «wasm» полностью себя оправдал, каждый запрос стал обрабатываться, в среднем, за 300 мс, вместо полутора секунд.
Более продвинутые бакенды пощупать не удалось, поскольку подходящих к использованию видеокарт на виртуалке доступно не было. Именно с этими бакендами связана необходимость ручного освобождения памяти. Дело в том, что при их использовании, для хранения весов модели используются текстуры WebGL, освобождать которые автоматически JavaScript не умеет.
Начиная с этого момента, бот заработал, но это было не очень увлекательно. Бот просто выполнял ход, выбирая случайным образом одну из наиболее вероятных позиций, но для того чтобы понять, какие альтернативы были у этого хода, приходилось лезть в лог. Настало время задуматься о визуализации.
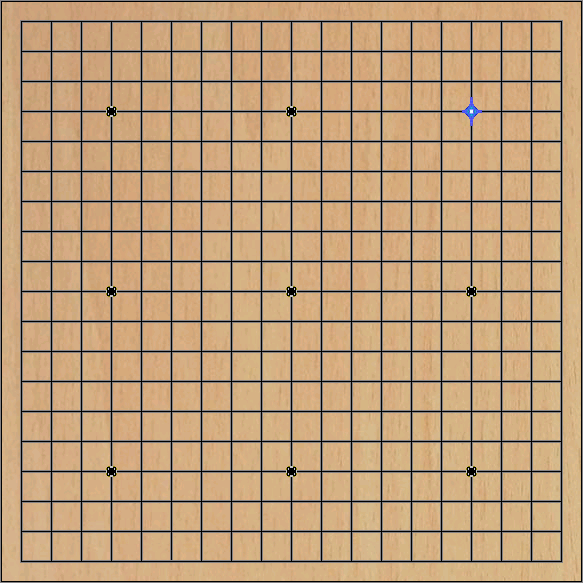
Идея нехитрая — просто собираем наиболее вероятные ходы и передаём их все скопом в UI, для отображения. На пустой доске (перейдя по ссылке надо немного подождать) видим одну звезду (сейчас их больше), что наводит на мысли. Доска-то у нас симметричная!
Кручу-верчу, запутать хочу
Ход в правый верхний звёздный пункт ("хоси"), считается, в определённой степени, традиционным. Играя туда, где у оппонента «находится сердце», первый игрок проявляет своё уважение. Сервер KGS — это, несомненно, то самое место, где традиции соблюдаются. Конечно, помимо «хоси», хотелось бы видеть "комоку", "такамоку", "сан-сан" и "мокухадзуси", но здесь, по всей видимости, свою негативную роль сыграло крайне малое количество партий, на которых производилось обучение.
const SIZE = 19;
function flipX(pos) {
const x = pos % SIZE;
pos -= x;
return pos + (SIZE - x - 1);
}
function flipY(pos) {
const y = (pos / SIZE) | 0;
pos -= y * SIZE;
return (SIZE - y - 1) * SIZE + pos;
}
function toRight(pos) {
const x = pos % SIZE;
const y = (pos / SIZE) | 0;
return x * SIZE + (SIZE - y - 1);
}
function toLeft(pos) {
const x = pos % SIZE;
const y = (pos / SIZE) | 0;
return (SIZE - x - 1) * SIZE + y;
}
Идеально обученная нейросеть выдавала бы одинаковый, с учётом поворота или отражения, ответ, вне зависимости от ориентации доски, но обучение нашей модели очень далеко от идеала. Если после поворота или отражения доски сеть выдаёт другой ответ, из соображений симметрии понятно, что предложенный ей ход так же хорош как и ход, полученный для оригинальной позиции. Это даёт нам 8 начальных ориентаций доски — своего рода различные точки зрения на одну и ту же позицию. Разумеется, при симметричном расположении камней, часть из них может совпадать друг с другом (так, для пустой доски, все 8 начальных позиций совпадают).
Кроме того, в Го существует эмпирическое правило: «лучший ход противника — это и твой лучший ход», которое действует не всегда, но достаточно часто. Изменяя знак в начальной расстановке камней, получаем ещё 8 позиций. Чтобы как-то отличить эти ходы от обычных, я отображаю их на доске другим цветом. Наиболее вероятные ходы отображаются крупными звёздами, менее вероятные мелкими:
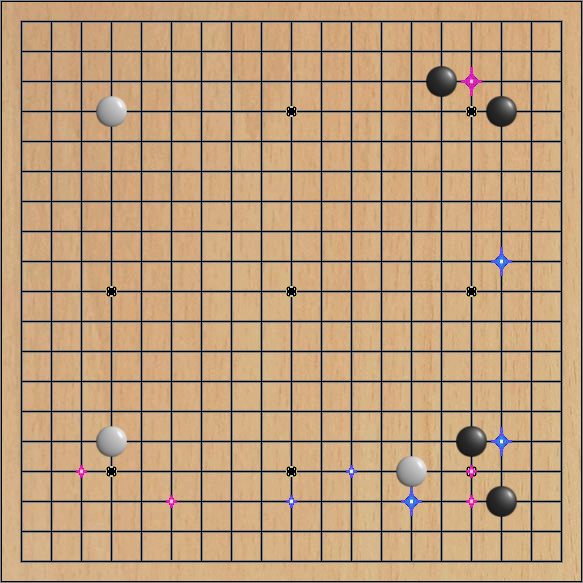
Есть ещё один важный момент, о котором стоит упомянуть. Своей игрой бот, в настоящее время, напоминает игрока с хорошей интуицией, но крайне рассеянного. Действуя по наитию, он бросается от одного тактического плана к другому, не доводя ни один из них до конца. Более того, поскольку, как я уже писал выше, модель недостаточно хорошо обучена, она вполне может порекомендовать ход, запрещённый правилами игры — самоубийственный или просто на пункт уже занятый камнем. Что касается правила Ко, то для его выполнения необходимо передавать боту дополнительную информацию — пункт, ход в который запрещён.
Хорошие ходы в Го можно разделить на «большие» и «срочные». Большие ходы позволяют эффективно захватывать территорию, срочные — защищают построения игрока от захвата и разрушения. Чтобы не проиграть с разгромным счётом, срочные ходы следует делать прежде больших. И как раз с этим у бота проблемы. Большие ходы модель предсказывает неплохо, но на явные угрозы практически не реагирует. Помимо интуиции, боту не помешают «безусловные рефлексы». Чтобы видеть эти рекомендации, я добавил в визуализацию зелёные звёзды. Крупная зелёная звезда, это ход, который бот выберет, даже не обращаясь за помощью к нейросети.
function analyze(board) {
let m = []; let r = []; let done = [];
for (let p = 0; p < SIZE * SIZE; p++) {
if (!isEmpty(board[p])) continue;
if (_.indexOf(done, p) >= 0) continue;
let g = [p]; let c = null; let e = [];
for (let i = 0; i < g.length; i++) {
m[ g[i] ] = r.length;
done.push(g[i]);
_.each([1, -1, SIZE, -SIZE], function(dir) {
let q = navigate(g[i], dir);
if (q < 0) return;
if (_.indexOf(g, q) >= 0) return;
if (isEnemy(board[q])) {
if (c === null) c = -1;
if (isFriend(c)) c = 0;
if (_.indexOf(e, q) < 0) e.push(q);
return;
}
if (isFriend(board[q])) {
if (c === null) c = 1;
if (isEnemy(c)) c = 0;
if (_.indexOf(e, q) < 0) e.push(q);
return;
}
g.push(q);
});
}
r.push({
type: 0,
group: g,
color: c,
edge: e
});
}
for (let p = 0; p < SIZE * SIZE; p++) {
if (_.indexOf(done, p) >= 0) continue;
let f = isFriend(board[p]);
let g = [p]; let d = []; let y = []; let e = [];
for (let i = 0; i < g.length; i++) {
m[ g[i] ] = r.length;
done.push(g[i]);
_.each([1, -1, SIZE, -SIZE], function(dir) {
let q = navigate(g[i], dir);
if (q < 0) return;
if (_.indexOf(g, q) >= 0) return;
if (isFriend(board[q])) {
if (!f) {
if (_.indexOf(e, q) < 0) e.push(q);
return;
} else {
if (_.indexOf(g, q) < 0) g.push(q);
}
} else if (isEnemy(board[q])) {
if (f) {
if (_.indexOf(e, q) < 0) e.push(q);
return;
} else {
if (_.indexOf(g, q) < 0) g.push(q);
}
} else {
if (_.indexOf(d, q) < 0) d.push(q);
let ix = m[q];
if (_.isUndefined(ix)) return;
if (!isEmpty(r[ix].type)) return;
if (f) {
if (isFriend(r[ix].color)) {
if (_.indexOf(y, q) < 0) y.push(q);
r[ix].isEye = true;
}
} else {
if (isEnemy(r[ix].color)) {
if (_.indexOf(y, q) < 0) y.push(q);
r[ix].isEye = true;
}
}
}
});
}
r.push({
type: f ? 1 : -1,
group: g,
dame: d,
eyes: y,
edge: e
});
}
return {
map: m,
res: r
}
}
Она строит, своего рода «карту доски», разделяя её на связные области. Для групп камней одного цвета учитываются дамэ, а для пустых пунктов ограничивающие камни. Если группа пустых пунктов граничит с камнями одного цвета, она считается территорией.
0 0 0 0 0 0 0 0 0 0 0 0 0 7 0 0 0 0 0
0 0 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 9 1 10 10 0 0 11 0 0 0 0 0 12 0 0 0 0 0
0 0 13 2 10 0 0 0 0 0 0 0 0 0 0 14 0 0 0
0 0 13 13 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 13 0 15 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 16 0 0 0
0 0 17 0 0 0 0 0 18 0 19 19 0 20 0 16 21 0 0
0 0 0 0 0 0 0 0 0 22 23 19 24 24 25 21 21 0 0
0 0 0 0 0 0 0 0 0 22 23 23 26 26 3 27 0 0 0
0 0 0 0 0 0 0 0 0 28 4 23 23 26 3 3 29 0 0
0 0 0 0 0 0 0 0 0 0 30 29 23 23 29 3 29 0 0
0 0 0 0 0 0 0 0 0 0 0 29 29 29 29 29 29 0 0
0 0 0 0 0 31 0 0 0 0 0 32 32 29 33 33 29 34 0
0 0 0 0 0 35 36 0 37 0 0 0 38 0 33 39 5 40 40
0 0 0 0 41 0 0 42 0 0 0 0 0 0 0 39 5 5 5
0 0 0 0 0 0 42 42 0 43 0 0 0 0 44 6 45 45 45
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 46 47 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Далее, в ход идут различного рода эвристики. Например, если бот видит несколько групп камней противника в положении "атари", он постарается захватить ту из них, которая больше размером. Если под «атари» находится группа камней бота, он постарается спасти её, но только при условии, что своим ходом он увеличивает количество "дамэ" группы и при этом не выходит на первую линию. Бот не будет заполнять камнями глаза своих групп и, по возможности, постарается поставить противнику двойное «атари». Вообще, здесь есть большой простор для творчества. Можно определять ситуации "гэта" и "ситё", просчитывать "защёлки", определять хорошие и плохие формы. И конечно, это та часть кода, которую просто необходимо покрыть юнит-тестами. Серьёзно, они уже помогли мне исправить несколько серьёзных багов!
Аппетит приходит во время еды
После конвертации из Keras, я получил модель, которую загружаю при помощи loadLayersModel, но TensorFlow.js умеет работать и с GraphModel тоже. В чём разница? GraphModel работает немного быстрее. Зато LayersModel можно дообучать в процессе использования. Разумеется, мне захотелось сделать это сразу же, как только я узнал об этом. Во многом пришлось действовать методом тыка (а также чтения документации) и вот к чему я пришёл:
board = new Float32Array(N * 19 * 19);
...
const xshape = [N, 1, 19, 19];
const xs = tf.tensor4d(board, xshape, 'float32');
const yshape = [N, 19 * 19];
const ys = tf.tensor2d(y, yshape, 'float32');
Здесь я заполняю сразу N начальных расстановок камней и соответствующие им N лучших ходов, в том же формате, в котором их отдаёт модель. Где взять данные для обучения? У нас есть сервер, на котором люди могут играть друг с другом или против бота. Никто не мешает мне сохранять сделанные ходы в БД, для последующего обучения модели. Ладно-ладно, ещё у нас есть записи игр c KGS-сервера, из которых Макс Памперла и Кевин Фергюсон использовали всего 100 партий (их там намного, намного больше). В общем, я сделал загрузчик, для разбора SGF-файлов и последующей подготовки данных для обучения бота.
const model = await tf.loadLayersModel(URL);
model.compile({optimizer: 'sgd', loss: 'categoricalCrossentropy', metrics: ['accuracy']});
Хотя в сохранённой модели имеются данные о настройках оптимизатора, если перед обучением не сказать ей «compile», дело кончится сообщением об ошибке. Ситуацию несколько оживляет тот факт, что одни и те же вещи в Keras и Tensorflow.js записываются немного по-разному. К счастью, на сайте Tensorflow имеется исчерпывающий документ на эту тему.
const h = await model.fit(xs, ys, {
batchSize: 100,
epochs: 3,
validationSplit: 0.1
});
xs.dispose();
ys.dispose();
Следующим, о чём следовало позаботиться, стало сохранение обученной модели. Здесь меня подстерегала засада. Вероятно, это связано с тем, что изначально Tensorflow.js разрабатывался для использования в браузерах, а не в Node.js, но «из коробки» простое сохранение на диск не работало. К счастью, Google помог справиться с этой проблемой:
const {nodeFileSystemRouter} = require('@tensorflow/tfjs-node/dist/io/file_system');
...
tf.io.registerLoadRouter(nodeFileSystemRouter);
tf.io.registerSaveRouter(nodeFileSystemRouter);
...
await model.save(`file:///tmp/${savePath}`);
Разумеется, работы здесь ещё непочатый край. Можно экспериментировать с размерами батча и количеством эпох. Часть слоёв можно «заморозить», чтобы улучшить производительность обучения (имеет смысл сделать это для свёрточных слоёв модели, поскольку именно они выполняют всю черновую позицию по определению «хороших» и «плохих» форм). Сколько и каких слоёв замораживать — это тоже подходящая тема для экспериментов. Даже простое разделение данных на обучающие и тестовые — далеко не такая простая задача, как может показаться на первый взгляд. Позиции, загруженные в рамках одной партии, зависят друг от друга. Выбор тестовых данных из той же серии может создать иллюзию эффективности обучения модели.
{
"validationData":null,
"params":
{
"epochs":3,
"initialEpoch":0,
"samples":900,
"steps":null,
"batchSize":100,
"verbose":1,
"doValidation":true,
"metrics":
[
"loss",
"acc",
"val_loss",
"val_acc"
]
}
,
"epoch":
[
0,
1,
2
]
,
"history":
{
"val_loss":
[
6.965572357177734,
6.191959381103516,
6.181119918823242
]
,
"val_acc":
[
0.019999999552965164,
0.029999999329447746,
0.019999999552965164
]
,
"loss":
[
9.069977760314941,
5.387154579162598,
4.876873970031738
]
,
"acc":
[
0.018888888880610466,
0.057777777314186096,
0.09222222119569778
]
}
}На обработку этой тысячи позиций потребовалось более 6 минут, с использованием «wasm»-бакенда. Машинное обучение — это тот вид деятельности, в которой производительность имеет первостепенное значение.
Что дальше?
Хотя игра бота и выглядит разумной, она очень далека от идеала. К сожалению, используемую в настоящий момент модель можно обучать лишь до определённого предела. В процессе обучения, качество её игры будет улучшаться всё меньше и меньше. Кроме того, существует проблема возможного переобучения. Бороться с этим можно только изменяя топологию модели, экспериментируя с количеством слоёв, фильтров, функциями активации и прочим. Также, следует подумать о более адекватном представлении входных данных. Используемая в настоящий момент однослойная схема кодирования — не лучший выбор. Мы можем передавать модели гораздо больше полезных данных.
- Группы вражеских камней с одним дамэ (которые можно захватить одним ходом)
- Группы вражеских камней с двумя дамэ
- Группы вражеских камней с тремя дамэ и более
- Группы своих камней с одним дамэ (защищать эти группы необходимо не всегда, но очень часто)
- Группы своих камней с двумя дамэ (угроза атари)
- Группы своих камней с тремя дамэ и более (камни в относительной безопасности)
- Пункты, ход на которые запрещён (по крайней мере, правилом Ко)
- Пункты, ход на которые подсказывают «безусловные рефлексы»
Два последних слоя — в определённой степени, чит. При достаточном обучении, модель должна «разобраться» во всём сама, но это упирается в вычислительные ресурсы. Если дополнительная информация позволит ускорить обучение, почему бы её не передавать? Функция analyze всё равно её собирает.
Другой важный момент — завершение игры. Ближе к концу партии, полезных ходов становится всё меньше, а «больших» ходов не остаётся вовсе. Эта фаза игры называется ёсэ и в ней разыгрываются последние очки. Когда ходов не остаётся вовсе, один из игроков говорит «пас» и пропускает ход. Если, вслед за ним, «пас» говорит и его противник, игра завершается и начинается фаза подсчёта очков. Бот, в настоящее время, «пас» говорить не умеет, а вместо этого начинает делать глупые ходы, заполняя свою территорию. Эту проблему можно решить, добавив дополнительный, 362-ой пункт в массив выходных данных. Единичка в этом пункте будет означать, что модель пропускает ход.
Этот подход очень требователен к производительности. Для качественной работы MCTS, партия должна быть доиграна до конца тысячи раз. Разумеется, это далеко за пределами моих вычислительных возможностей. Доигрывание можно выполнять всего на несколько ходов вперёд, но оценка промежуточной позиции в Го также является не тривиальной задачей. В Alpha Go, для этой цели, используется третья модель — «оценки».
С моделью оценки связана ещё одна важная возможность. Помимо штатного завершения игры, хороший бот должен уметь признавать своё поражение. Это часть этикета Го — видя своё неминуемое поражение, игрок должен вовремя завершить партию, не злоупотребляя более личным временем победителя. При этом, не следует сдаваться слишком рано, пока ещё остаётся возможность для победы.
Также, очевидным моментом является то, что никакое «обучение с учителем» не способно натренировать сеть так, чтобы она играла лучше тех людей, на партиях которых её обучали. Эту высоту можно покорить лишь используя "обучение с подкреплением" таким образом, как это делают Alpha Go и AlphaGo Zero. Бот должен сыграть сам с собой миллионы партий, чтобы выйти на их уровень. Разумеется, для простого смертного, эта цель недостижима, но обучение с подкреплением вполне можно использовать для более простых игр, таких как "Атари Го" или Hex на небольших досках. Есть много хороших задач, чтобы потренироваться.
Автор: Валентин

