Об изменчивых методах объекта Math в JavaScript

Сегодня мы публикуем перевод статьи о математических вычислениях в JavaScript, которая представляет собой письменный вариант выступления её автора на WaffleJS. А само это выступление было чем-то вроде продолжения этой беседы в Twitter.

Математическое образование

Интерес к математике

Всё началось с моего математического образования, с получением которого я несколько затянул. Когда я изучал компьютерные науки, я мог общаться с преподавателями математики мирового уровня, но эту возможность я упустил. Мне не нравилась математика: изучаемые темы были весьма далеки от практики. Кроме того, я тогда уже был выведен из равновесия глубоко теоретической программой компьютерного обучения. Я тогда полагал, что она оторвана от жизни, и, по большей части, продолжаю так думать.

Но вот, через несколько лет после того, как я завершил учёбу, во мне проснулась жажда к изучению математики. Меня вдохновляло то, какой эффект на мою работу и на моё хобби способно оказать даже небольшое приложение математических знаний. Но у меня не было чёткого плана учёбы.

Тогда, в 2012 году, я нашёл способ изучать математику, начав работу над проектом Simple Statistics. С тех пор я расширял и поддерживал этот проект. Сейчас в его состав входят реализации множества алгоритмов, он оказался одной из самых «звёздных» математических JavaScript-библиотек. И, по всей видимости, люди реально пользуются этой библиотекой.

Но работу я начинал в 2012 году. Если говорить о том, как за это время изменились технологии, то это было очень и очень давно. С тех пор вышло 8 LTS-релизов Node.js. С тех пор сильно изменился и сам JavaSript, и среды, в которых работают программы, написанные на этом языке. В 2012 ещё не существовало библиотеки React, тогда ещё не был сделан первый коммит в проект Babel.

Ход времени

За эти годы я заметил то, что мои тесты давали сбои при обновлении Node.js. Например, у меня может быть примерно такой тест:

t.equal(ss.gamma(11.54), 13098426.039156161);

Этот тест нормально работает в Node.js v10, но «ломается» в Node.js v12. И тут проверяется не какой-то сверхсложный метод: функция gamma реализована с использованием стандартных функций JavaScript — Math.pow, Math.sqrt и Math.sin.

Арифметика

Знаю, о чём вы можете тут подумать: об арифметике. В Twitter периодически разгораются жаркие дискуссии из-за результатов вычисления следующего выражения:

0.1 + 0.2 = 0.30000000000000004

Но, как я уже писал, так себя ведут все популярные языки программирования, даже старомодные и педантичные — вроде Haskell. Арифметические вычисления с плавающей точкой могут выглядеть странно, но они ведут себя единообразно, их поведение отлично документировано. А именно, речь идёт о стандарте IEEE 754, требования которого строго реализованы в языках программирования. Итак, значит проблема не в арифметике: реализация сложения, вычитания, деления и умножения в языках программирование, можно сказать, «высечена в камне».

Объект Math

Моя проблема крылась в стандартном JavaScript-объекте Math. В частности — во всех методах этого объекта.

Методы, такие, как Math.sin, Math.cos, Math.exp, Math.pow, Math.tan — это базовые ингредиенты для геометрических и других вычислений. Когда я это понял, я начал по отдельности изучать изменения в поведении базовых методов объекта Math в разных версиях Node.js. Вот примеры.

Вычисление Math.tanh(0.1):

// Node 4
0.09966799462495590234
// Node 6
0.09966799462495581907

Вычисление Math.pow(1/3, 3):

// Node 10
0.03703703703703703498
// Node 12
0.03703703703703702804

Ещё хуже то, что эта проблема проявляется не только в Node.js. Такое же происходит и в браузерах, и в других средах, поддерживающих JavaScript.

Это ведёт нас к следующему вопросу: а что такое математические вычисления?

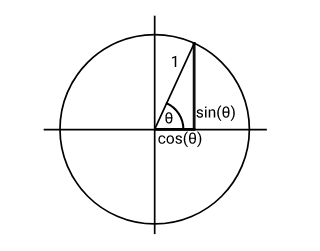
Графическое представление вычислений

Тригонометрические методы легко визуализировать. Если в вашем распоряжении имеется единичный круг и несколько месяцев старших классов средней школы, то вы знаете, что косинус и синус представляют собой координаты некоей точки на краю окружности, и то, что графики функций sin и cos выглядят как волны. На самом деле, в старших классах изучают получение этих значений, но используемый для этого метод — ряд Тейлора — полагается на бесконечный ряд, а компьютеру непросто решать подобные задачи.

Вот что можно узнать из Википедии по поводу алгоритма вычисления синуса: «Не существует стандартного алгоритма для вычисления синуса. IEEE 754-2008, самый широко используемый стандарт для вычислений с плавающей точкой, не затрагивает вычисление тригонометрических функций наподобие синуса».

Компьютеры используют множество различных приближений и алгоритмов для выполнения вычислений, нечто вроде CORDIC, всяческих хитрых приёмов и справочных таблиц. Вся эта неоднородность объясняет наличие на GitHub множества fastmath-библиотек. Дело в том, что существует множество способов реализации метода Math.sin. Да и других функций тоже. Например, как известно, в Quake III Arena использовалась более быстрая замена стандартного метода вычисления обратного квадратного корня для ускорения рендеринга.

В результате математические вычисления — это результат реализации неких алгоритмов. На практике используется множество распространённых алгоритмов и их разновидностей.

Спецификация JavaScript, вместо того, чтобы указывать то, какой конкретно алгоритм нужно использовать в реализациях языка, даёт реализациям большое пространство для манёвра в том, что касается функций, применяемых в математических вычислениях.

Вот что по этому поводу говорится в стандарте (ECMA-262, 10 редакция, раздел 20.2.2):

«Поведение функций acos, acosh, asin, asinh, atan, atanh, atan2, cbrt, cos, cosh, exp, expm1, hypot, log,log1p, log2, log10, pow, random, sin, sinh, sqrt, tan и tanh здесь полностью не описано, за исключением требований, касающихся возвращения определённых результатов для конкретных значений аргументов, которые представляют собой заслуживающие внимания граничные случаи».

Не знаю, как устроена внутренняя деятельность членов комитета, ответственного за стандарт ECMA-262, но полагаю, что они сделали стандарт именно таким для того, чтобы в JavaScript не случилось бы кризиса совместимости в том случае, если Intel или AMD выпустят новые сверхбыстрые математические инструкции в своих свежих процессорах.

Из-за того, что существует множество широко используемых JavaScript-интерпретаторов, из-за того, что JavaScript часто применяется в браузерах, и между браузерами всё ещё наблюдается нечто вроде соревнования, и из за того, что даже популярные реализации JavaScript находятся под постоянным давлением и вынуждены быстро эволюционировать, обеспечивая наилучшую производительность… из-за этого всего мы имеем то, что имеем. Тот, кто пользуется JavaScript, регулярно будет сталкиваться с тем, что в разных реализациях результаты математических вычислений, выполняемых средствами объекта Math, различаются.

Это не имеет столь же большого значения в других интерпретируемых языках, так как они обычно имеют некие «канонические» реализации. Например, это справедливо для интерпретатора Python.

Где выполняются вычисления?

Теперь давайте поближе присмотримся к тому, где именно выполняются вычисления. В случае с JavaScript можно выделить три области, в которых производятся базовые математические вычисления:

1. Процессор.
2. Интерпретатор языка (C++ и C-код конкретной реализации JavaScript).
3. Код, написанный на JavaScript, например — код специализированных библиотек.

▍1. Процессор

Первой идеей, которая пришла мне в голову, когда я размышлял о местах, где производятся вычисления, стало то, что вычисления выполняются в процессоре. Я предположил, что так как процессоры реализуют выполнение арифметических вычислений, то они могут реализовывать и какие-то более сложные вычисления. Оказалось, что в процессорах есть инструкции для выполнения тригонометрических и других расчётов, но используются эти инструкции редко. Например, реализация вычисления синуса в процессорах с архитектурой x86 не пользовалась особой популярностью, так как эта реализация не обязательно оказывается быстрее, чем программные реализации (такие, в которых применяются арифметические операции процессора). К тому же, она и не обязательно точнее программных реализаций.

Компания Intel, кроме того, натерпелась позора из-за очень сильного завышения точности тригонометрических операций в документации. Подобные ошибки особенно трагичны из-за того, что микрочип, в отличие от программы, не пропатчишь.

▍2. Интерпретатор языка

Вот как устроены подсистемы выполнения вычислений в большинстве реализаций JavaScript. Они реализуют эти подсистемы различными способами.

• Движки V8 и SpiderMonkey используют для вычислений порты библиотеки fdlibm, немного различающиеся. Эта библиотека, изначально написанная в Sun Microsystems, передавалась из поколения в поколение.
• В JavaScriptCore (Safari) для выполнения большинства операций используется библиотека cmath.
• В Internet Explorer используется и cmath, и некоторые блоки кода, написанные на ассемблере. Тут даже использовались и тригонометрические методы процессоров — в том случае, если браузер компилировали для процессоров, которые имели подобные инструкции.

По историческим причинам менялись средства, используемые для выполнения вычислений в разных JS-движках. Так, в V8 использовалось собственное решение для вычислений, затем применялся JavaScript-порт fdlibm, а уже потом — C-версия fdlibm.

▍Почему это — проблема?

Дело тут в том, что всё это снижает возможности JavaScript по выдаче единообразных результатов при решении любых задач, предусматривающих математические вычисления. Это особенно сильно бьёт по сфере Data Science. Мне хотелось бы, чтобы JavaScript лучше подходил бы для выполнения Data Science-расчётов в браузере. При этом невозможность выдавать единообразные результаты означает усугубление кризиса воспроизводимости, характерного для всех наук. Это — уже не говоря о некоторых других проблемах JavaScript, таких, как особенности типизации чисел и отсутствие широко используемой библиотеки для работы с дата-фреймами.

▍3. Использование специализированных библиотек

Существует надёжный способ выполнения вычислений в JavaScript, который нам доступен. Он заключается в использовании специализированных библиотек. Так, библиотека stdlib реализует высокоуровневые вычисления, используя лишь арифметические операции. Арифметические вычисления полностью описаны в спецификациях, стандартны, поэтому результаты, выдаваемые stdlib дают нам, независимо от платформы, на которой выполняется код, совершенно единообразные результаты.

Это достигается ценой сложности и скорости решений. Методы stdlib не так быстры, как встроенные. К тому же, для того, чтобы «просто посчитать синус», нужно подключать к проекту целую библиотеку.

Но, если мыслить шире, это совершенно нормально. Платформа WebAssembly, например, не даёт программисту никаких средств для выполнения высокоуровневых математических вычислений. В документации к ней рекомендуется самостоятельно включать реализации соответствующих механизмов в собственные модули:

«WebAssembly не включает в себя собственных реализаций математических функций — вроде sin, cos, exp, pow и так далее. Стратегия WebAssembly в отношении подобных функций заключается в том, чтобы позволить разработчикам реализовать их в качестве библиотечных инструментов в самой платформе WebAssembly (обратите внимание на то, что инструкции sin и cos платформы x86 медленны и неточны, и в наши дни ими, в любом случае, стараются не пользоваться)».

Именно так всегда и работали компилируемые языки: когда компилируют программу, написанную на C, методы, импортированные из math.h, включаются в скомпилированную программу.

Использование значения epsilon

Если некто не хочет включать в свой JavaScript-проект библиотеку stdlib для выполнения вычислений, но при этом нуждается в тестировании кода, выполняющего некие сложные вычисления, то ему, возможно, стоит прибегнуть к способу, который уже сейчас используется в библиотеке simple-statistics. Речь идёт об использовании значения epsilon, задающего границы, в пределах которых различия чисел не учитываются. Если рассматривать варианты использования символа epsilon в математике, то можно сказать, что я говорю здесь о нём как о «произвольном маленьком положительном значении». В simple-statistics используется значение epsilon, равное 0.0001.

Если нужно выяснить, равны ли два числа — проверяется условие вида Math.abs(result — expected) < epsilon. Если это условие оказывается истинным, то можно сказать, что разница между числами укладывается в заданный диапазон и счесть их равными.

Дополнения

▍Точность

Комментаторы в Twitter указали на то, что вариации в результатах, полученных в примере, находятся за пределами количества значащих цифр числа с плавающей запятой. С технической точки зрения это правильно, и это означает, что можно найти более точный способ сравнения чисел, чем тот, который предусматривает использование значения epsilon. Но на практике тут та же история — цифры, находящиеся в конце числа, влияют на результат и вносят неточности в итоговый результат. Кроме того, приведённые здесь примеры нельзя назвать исчерпывающими. Дело в том, что особенности реализации JavaScript-интерпретаторов способны, не отступая от спецификации, привести к появлению различий в большей части числовых результатов.

▍JavaScript

Я не хочу критиковать JavaScript. Я полагаю, что JavaScript пошёл на оправданный компромисс с учётом неопределённости будущего и того, на каком количестве платформ создаются реализации языка. Надо сказать, очень сложно напрямую сравнивать JavaScript и другие языки. Дело тут в экосистеме JavaScript. То, что одновременно существует множество интерпретаторов одного и того же языка, совершенно нетипично для других языков. И это, кроме того, является одной из главных сильных сторон JavaScript. Далее, нельзя не сказать о том, что это явления совсем другого плана, чем те, которые происходят в самом языке. А JavaScript со временем меняется и в нём появляется много хорошего.

▍Stdlib или epsilon?

Полагаю, что на практике в большинстве случаев стоит использовать именно подход, подразумевающий применение значения epsilon. Библиотека stdlib — это замечательный мощный инструмент, но цена включения в проект дополнительной библиотеки для математических вычислений может оказаться достаточно высокой. А в большинстве случаев небольшие расхождения в результатах вычислений не имеют никакого значения для приложений.

Итоги

Здесь мне хотелось бы сделать выводы из вышесказанного и поделиться некоторыми мыслями.

1. То, что находится внутри некоей системы, редко является тем, что там ожидается увидеть. Используемый в наши дни технологический стек очень сильно оптимизирован. При этом множество оптимизаций — это всего лишь «грязные хаки». Например, количество машинных инструкций, необходимых для того, чтобы функция Math.sin возвратила бы результат, зависит от того, что передано на вход этой функции, так как существует множество особых случаев. Когда нужно решить некую сложную задачу, наподобие сортировки массива, часто в системе существует несколько алгоритмов, из которых интерпретатор, стремясь решить задачу, выбирает наиболее подходящий. В целом можно отметить, что в интерпретируемых языках нагрузка на систему, создаваемая сходными операциями, может меняться в зависимости от конкретной ситуации.
2. Рекомендую не слишком сильно доверять компьютерным системам. То, что я видел, тестируя свою библиотеку в разных версиях Node.js, должно было быть вызвано ошибкой в библиотеке для тестирования, или в коде тестов, или в самой библиотеке simply-statistics. Но в данном случае, когда я копнул глубже, оказалось, что причина ошибки находится там, где её совсем не ждут увидеть. Она — в самой реализации языка.
3. Код пишут люди, они же придумывают алгоритмы. Читая код реализации V8, чувствуешь огромную благодарность тем одарённым программистам, которые создают интерпретаторы. Но тут же понимаешь, что программы создают люди. А люди совершают ошибки, и, что ясно видно в сфере алгоритмов для математических вычислений, им всегда есть что улучшать.

Уважаемые читатели! Сталкивались ли вы с проблемами, касающимися изменений результатов вычислений при переходе на новые версии Node.js?

Автор: ru_vds

Источник