Эту статью следовало бы назвать «генерирование комбинаций шестерен гитары китайского токарного станка для подбора шага подачи с помощью скрипта на JavaScript», но это звучит не так интригующе.

Самый дешевый токарный станок с Aliexpress MX-180V удивительным образом веселит меня с самого своего появления в моей домашней мастерской уже больше полугода. Несмотря на то, что китайцы забыли прикрутить его к ящику, вследствие чего была помята лицевая панель.


Несмотря на неспособность этого устройства нарезать левую резьбу, вопреки клятвам продавца, что может. Несмотря на то, что входившая в комплектацию отвертка, разлетелась после первого к ней прикосновения.

Несмотря, наконец, на низкое качество изготовления данного прибора, я им пользуюсь, изготавливаю нужные мне детальки и, в целом, накапливаю скилл. Для меня прелесть домашних станков состоит в том, что не нужно рыться в мусоре, в поисках чего-то похожего на нечто необходимое, а просто самому это делать. Это самый прямой путь от идеи к воплощению.
Так, постепенно, очередь дошла и до нарезания резьб. Потренироваться я решил на гвозде диаметром 6 мм, значит, чтобы ничего не обтачивать, это и будет диаметром болта с шагом резьбы 1 мм, для которого у меня была гайка. По таблице, которая находится на корпусе станка, нашел для выбранного шага необходимую комбинацию шестерен.
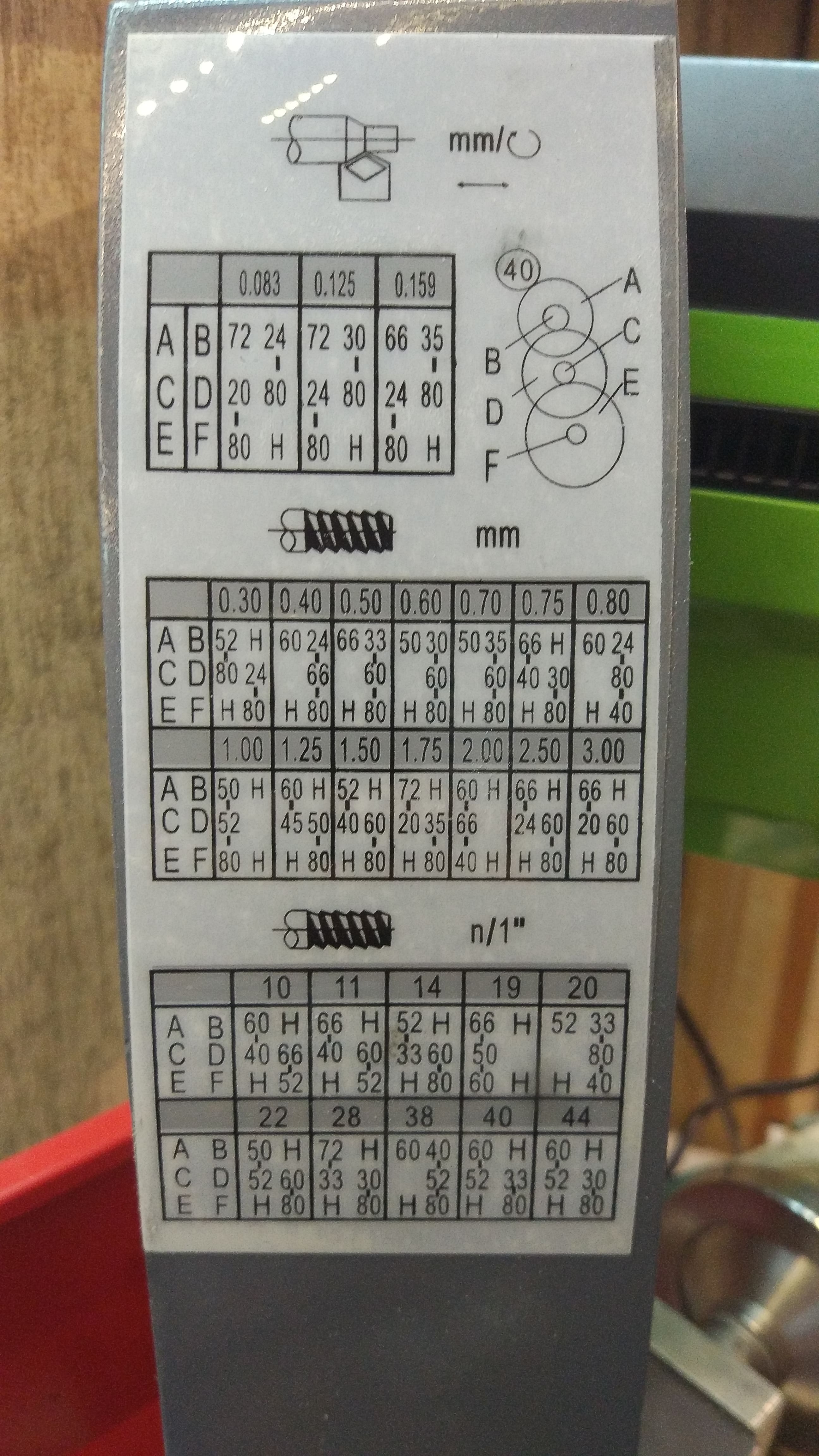
На валу шестерня с 80 зубами, затем 52, а между этой шестернёй и шпинделем должна стоять шестеренка с 50 зубами. Но среди 10 шестерен в моём наборе с 50 зубами не было.

Тут я начал в очередной раз расстраиваться, ну как же так, братья китайцы! Окончательно меня добил тот факт, что в моём наборе не было еще и второй шестерни на 80 зубов и 66, и 33-х-зубых шестерен. Немного поразмыслив, я понял, что для подачи в 1 мм на оборот важно лишь соотношение зубов на шпинделе и на валу, а промежуточные шестерни могут быть любыми, главное, чтобы они помещались туда. В итоге, первую в своей жизни резьбу М6x1 с помощью резца, а не плашки, я нарезал!

Одно только омрачало радостность этого события, несоответствие таблицы наличествующим у меня шестерням. Это означало, что теперь я не смогу просто так взять, посмотреть на таблицу и нарезать нужную резьбу, когда потребуется. Придется каждый раз думать, как поставить шестерни, каждый раз заново считать. В общем, с таблицей гораздо удобнее. Так судьба заставила меня углубиться в детали конструкции гитары и тонкости расчетов передаточных чисел редукторов.
Устройство редуктора не сложно и схематично четыре способа установки шестеренок (безотносительно их диаметров) можно изобразить так:
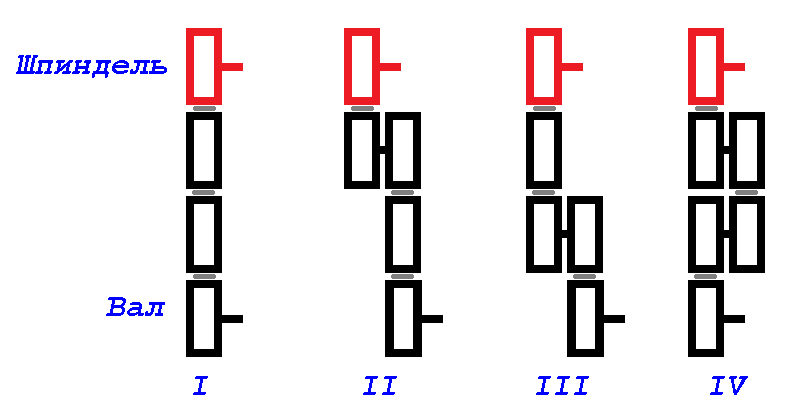
Для определенности будем называть их схемами зацепления. Мне было необходимо выяснить, какие комбинации шестерен допустимы с точки зрения возможности установки их в направляющую рейку, которая может поворачиваться вокруг оси вала и на которой фиксируются две оси промежуточных шестерен.

Верхняя ось не должна касаться шкива шпинделя, а потому первая ведомая шестерня не должна иметь менее 52 зубов. Кроме того, направляющая рейка не должна быть повернута слишком близко у валу шпинделя, во избежание задевания магнитиков тахометра.


Физическая попытка брутфорса этой задачи показала, что допустимых комбинаций достаточно много. На листочке уже стало не хватать места для ещё не проверенных наборов, я стал путаться. Был велик шанс пропустить комбинацию, либо наоборот, записать уже проверенную. Желание заниматься слепым перебором вариантов, сидя в неудобной позе перед станком, улетучилось очень быстро. Сколько и какие вообще комбинации и подачи возможны на этом станке? Требовалось призвать на помощь теорию, а труды по перебору вариантов возложить на компьютер, чтобы зря не стоял.
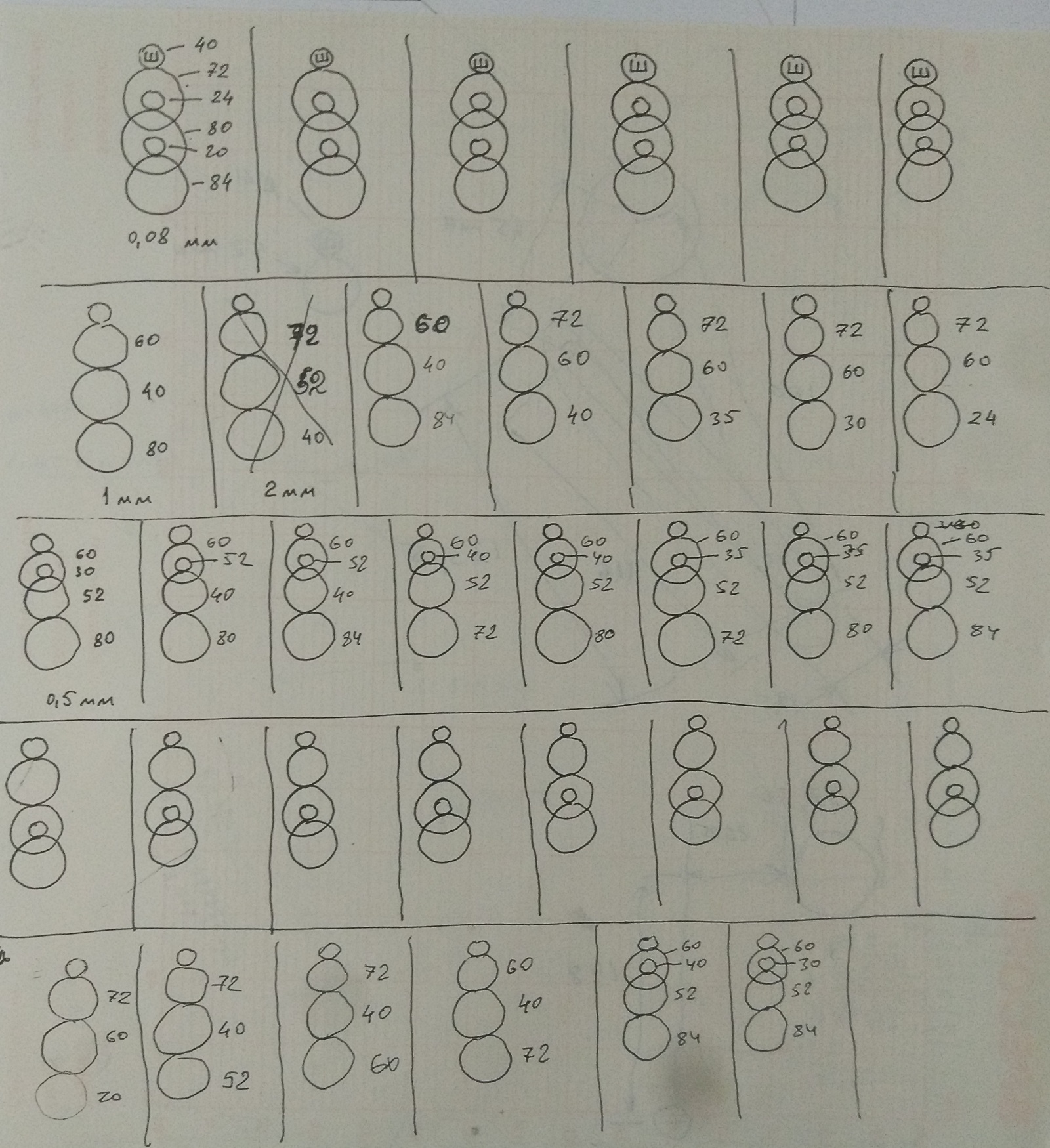
Надо будет найти или написать генератор размещений без повторений, так как каждая шестерня у меня только в одном экземпляре. Способов выбрать из 10 вариантов 3, 4 и 5 шестерен достаточно много, но какие-то из них, очевидно, следует отбросить из-за геометрических соображений. Понадобится фильтр, пропускающий только подходящие наборы шестерен. После фильтрации наверняка останется много комбинаций, которые будут давать одинаковый шаг подачи, не отличаясь при этом схемами зацепления и наборами шестерен, т.е. будут эквивалентные перестановки. От них тоже следует избавиться.
Не раздумывая, программировать решил на JS, хотя мог и на C++, но в своей практике я ещё не сталкивался с задачей, которую нельзя было бы решить в браузерном JS, когда дело не доходит до сброса данных на диск. В этом способе меня привлекает минимализм и достаточность инфраструктуры, блокнот и браузер, всё остальное лишне. Язык дает алгоритмизацию, браузер – графический интерфейс, интерпретатор и отладчик. Любую библиотеку можно либо быстро написать самому, либо найти и скачать. Когда не занимаешься промышленным или коммерческим программированием, то достаточно, просто, универсального калькулятора.
Генератор размещений я нашел и адаптировал быстро. Его назначение в программе переставлять индексы массива, в котором будут храниться экземпляры шестерен. Здесь в функции search генерируются размещения, а прошедшие фильтр запихиваются в массив result функцией test. Кроме того, в последней функции вычисляется подача. Для определенности обозначим все шестерни так, как на рисунке.

Если выписать формулы для расчета подачи, как функции шага вала подачи и числа зубов шестерен для каждой из схем зацепления:
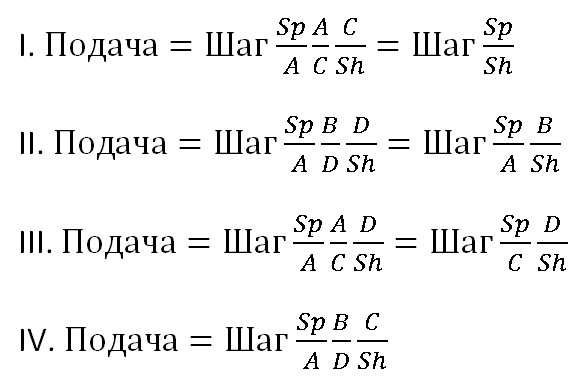
то оказывается, что их можно свести к одной, совпадающей с IV, если положить:
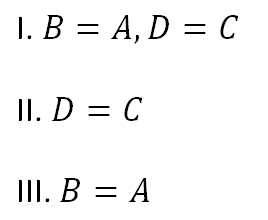
Чтобы разработать фильтр следует поподробнее остановиться на геометрических параметрах гитары. Оси шпинделя, вала и верхней промежуточной шестерни образуют треугольник.
Сторона L которого измеряется непосредственно, а остальные вычисляются из радиусов шестерен. Радиус шестерен меньше их наружного радиуса на величину перехлеста при зацеплении. Поскольку шестерни изготовлены не идеально величину перехлеста следует установить эмпирически. Перехлест должен быть таким, чтобы обеспечивал зацепление, но предотвращал заклинивание шестерен. В моём случае он оказался равен 1 мм. На сторону S накладывается следующее ограничение, ось верхней промежуточной шестерни не должна касаться шкива шпинделя. Она измеряется непосредственно, когда направляющая с осью верхнем положении повернута максимально близко к шпинделю, ось при этом должна почти касаться шкива. Расстояние V не может быть больше дистанции между осью вала и верхней промежуточной осью, отодвинутой до упора вверх по пазу. Также следует наложить ограничение на угол между L и V. Повернув рейку без шестерен и осей максимально близко к шпинделю, измерить или вычислить расстояние S между осью шпинделя и верхней точкой направляющей и рассчитать угол по формуле
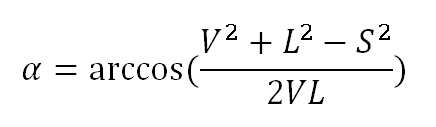
Здесь V это расстояние от оси вала до верхней точки направляющей, а не до верхней точки паза (это может быть произвольная точка рельсы, главное, чтобы расстояния V и S измерялись до неё). По этой же формуле будет вычисляться угол при тестировании, но расстояния S и V будут зависеть от радиусов шестерен.
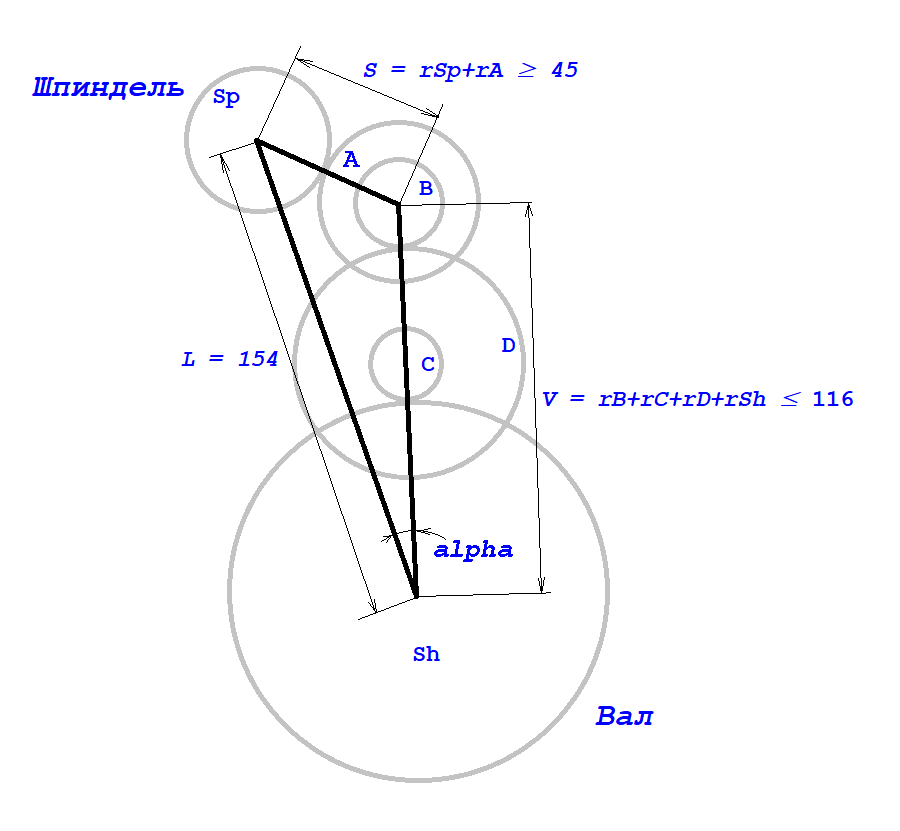
Кроме этого, шестерня B не может быть больше A, а C не может быть больше, чем D. D не должна касаться вала, а C не должна цепляться за A, при зацеплении B и D.
После того, как список удачных комбинаций построен следует избавить его от избыточности с помощью функции eliminate. Это осуществляется простым поиском уникальных в каком-либо отношении решений. Можно использовать уникальность шага, или уникальность набора шестерен и тому подобное.
В моем случае получается 753 комбинации, которые отличаются подачей, числом шестерен и их набором. Уникальных подач всего 220. Конечно, многие из них не являются общеупотребительными или вообще не применяются, зато присутствуют дюймовые.

Работая над этим текстом меня не покидала мысль, что способ решения этой задачи находится на уровне 5 класса, о котором даже стыдно рассказывать. Просто в данном случае результат (таблица подач) гораздо важнее способа её получения. Однако, станки, гитары, схемы редукторов, шестерни у каждого могут быть разными и не плохо было бы иметь в виду хотя бы один из подходов к построению такой таблицы.
В заключение привожу полный текст скрипта, который снабжен достаточным количеством комментариев, учитывая вышеизложенное.
<!DOCTYPE html>
<html>
<body>
<div>
<textarea id="out"></textarea>
</div>
<div><button onclick="calc()">Calc</button></div>
<script>
var out = document.getElementById("out");
out.style.width = '600px';
out.style.height = '500px';
// Класс шестеренок
function gear(n,r){
var overlap = 1.0;//полуперекрытие зубьев при зацеплении
this.n = n;//число зубьев
this.r = r - overlap;//радиус
this.R = r;
}
//Создаем шестерни
var gears = [
new gear(40,20.50),//на шпинделе
new gear(20,10.90),
new gear(24,12.85),
new gear(30,15.95),
new gear(35,18.50),
new gear(40,21.00),
new gear(52,26.90),
new gear(60,30.85),
new gear(72,36.90),
new gear(80,40.95),
new gear(84,43.00)
];
var sh_sp = 154.0,//ось вала - ось шпинделя (база)
sh_rail = 134.5,//ось вала - верхняя точка рейки
sp_rail = 24.0;//ось шпинделя - верхняя точка рейки при касании
//минимальный угол между базой и рейкой
var alfa_min = Math.acos((sh_rail*sh_rail+sh_sp*sh_sp-sp_rail*sp_rail)/
(2*sh_rail*sh_sp));
var shaft_step = 2.0,//mm
sp_oa_min = 45.0,//минимальное расстояние между осью шпинделя
//и верхней промежуточной осью
sh_oa_max = 116.0;//максимальное расстояние между осью вала
//и верхней промежуточной осью
//Генератор размещений без повторений из множества n чисел по m штук
function nextVar(a, n, m){
var j, s;
do{//ищем следующее размещение
j = n - 2;
while (j != -1 && a[j] >= a[j + 1]) j--;
if (j == -1)
return false; //размещений больше нет
var k = n - 1;
while (a[j] >= a[k]) k--;
s = a[j]; a[j] = a[k]; a[k] = s;//swap(a, j, k);
var l = j + 1, r = n - 1;//сортируем оставшуюся часть последовательности
while (l < r){
s = a[l]; a[l] = a[r]; a[r] = s;//swap(a, l++, r--);
l++; r--;
}
} while (j > m - 1);
return true;
}
//
// Sp
// A B
// C D
// ShSh
//
function test(a,v,result){
var Sh, D, C, B, A, Sp;
switch(v){
case 0:// III
Sh = gears[a[0]];//на валу
C = gears[a[1]];
D = C;
A = gears[a[2]];
B = A;
Sp = gears[0];//шпиндель
break;
case 1:// IV
Sh = gears[a[0]];//на валу
D = gears[a[1]];
C = D;
B = gears[a[2]];
A = gears[a[3]];
Sp = gears[0];//шпиндель
break;
case 2:// IV
Sh = gears[a[0]];//на валу
D = gears[a[1]];
C = gears[a[2]];
A = gears[a[3]];
B = A;
Sp = gears[0];//шпиндель
break;
case 3:// V
Sh = gears[a[0]];//на валу
C = gears[a[1]];
D = gears[a[2]];
B = gears[a[3]];
A = gears[a[4]];
Sp = gears[0];//шпиндель
break;
default: return false;
}
//
var S = Sp.r + A.r;
var V = Sh.r + D.r + C.r + B.r;
var L = sh_sp;
//направляющая гитары не должна поворачиваться слишком близко к шпинделю
if(Math.acos((V*V+L*L-S*S)/(2*V*L)) < alfa_min) return false;
//ось AB не должна касаться шкива
if(S < sp_oa_min) return false;
//ограниченная длина направляющей гитары для оси AB
if(V > sh_oa_max) return false;
//шестерня A должна доставать до шестерни шпинделя
if(S + V <= L) return false;
//шестерня B не должна быть больше чем A
if(B.r > A.r) return false;
//шестерня C не должна быть больше чем D
if(C.r > D.r) return false;
//шестерни C и D не должны задевать ось вала
if(D.r != C.r)
if(Sh.r-9.0 < D.R-C.r) return false;
//шестерня A не должна задевать шестерню C при зацеплении B и D
if(D.r != C.r)
if(A.R-B.r >= D.r-C.R) return false;
//Вычисляем шаг для данного набора и округляем его
var d = 1000;
step = Math.ceil(d*shaft_step*Sp.n*B.n*C.n/(A.n*D.n*Sh.n))/d;
//
switch(v){
case 0: result.push([step,1,Sh.n,C.n,A.n]); break;// III
case 1: result.push([step,2,Sh.n,D.n,B.n,A.n]); break;// IV
case 2: result.push([step,3,Sh.n,D.n,C.n,A.n]); break;// IV
case 3: result.push([step,4,Sh.n,C.n,D.n,B.n,A.n]); break;// V
}
//
return true;
}
//Поиск удачных комбинаций
function search(result){
var k = [3,4,4,5];//число шестерен в наборе
for(var v=0;v<4;v++){
var G = [1,2,3,4,5,6,7,8,9,10];
do{
test(G,v,result);//фильтрация комбинации
} while (nextVar(G, 10, k[v]));
}
}
//Устранение избыточности
function eliminate(result){
//используем входной массив сразу в качестве выходного
var J = 1, I = result.length;
for(var i=1;i<I;i++){
var f1 = true, f2 = true, f3 = false;
for(var j=0;j<J;j++){
if(result[j][0] == result[i][0]){//если шаги равны
f1 = false;
if(result[j].length == result[i].length){//если количества шестеренок равное
f2 = false;
var a1 = result[j].slice().sort();
var a2 = result[i].slice().sort();
for(var n=0;n<a1.length;n++)
if(a1[n] != a2[n]){
f3 = true;//наборы разные
break;
}
}
}
}
if(f1)//уникальный шаг
//if(f1 || f2 || (!f2 && f3))//уникальные комбинации
result[J++] = result[i];
}
result.splice(J, I-J);//удалим лишние и упорядочим по подаче
result.sort(function(a, b){return a[0]-b[0]});
}
//
function calc() {
var result = [];
search(result);
eliminate(result);
var a = [];
for(var i=0;i<result.length;i++)
a.push(result[i].join("t"));
out.value = a.join("n");
}
</script>
</body>
</html>
Автор: Олег Петрухин






