Готовые примеры
Примеры подготовлены на базе движка OpenGlobus, который в данном случае используется как обертка над чистым Javascript WebGL.
— Пример для 2D случая
— Пример для 3D случая (используйте клавиши W,S,A,D,Q,E и курсор для перемещения)
Вступление
В процессе работы над картографической библиотекой мне потребовался инструмент позволяющий рисовать линии разной толщины. Конечно в WebGL есть механизм рисования линий, но задавать толщину линии к сожалению нельзя. Поэтому линии приходится рисовать полигонами, лучше сказать треугольниками. В интернете можно найти несколько отличных статей, как «триангулировать» линию, какие сложности при этом возникают и как их решать. К своему сожалению, я не нашел такую статью, из которой я мог бы скопировать код и использовать в своем шейдере.
После многочисленных часов проведенных с карандашом и бумагой за рисованием алгоритма, а затем многочисленных часов отладки совсем не сложного glsl шейдера, я наконец пришел к результату, которого можно было бы достичь гораздо быстрее. Надеюсь описанный далее подход рендеринга полигональных линий в WebGL сбережет время вашей жизни, которое в противном случае ушло бы на реализацию этой задачи!
Рисование линии в двухмерном пространстве
В моем движке для шейдеров рисования линий в двумерном и трехмерном пространствах используется практически один и тот же код. Разница лишь в том, что для трехмерного случая добавлено проецирование трехмерных координат линии на экран, затем тот же алгоритм.
Существует расхожая практика для придания линиям толщины — представить каждый сегмент линии прямоугольником. Самое простое представление толстой линии выглядит так (рис. 1):
(рис. 1)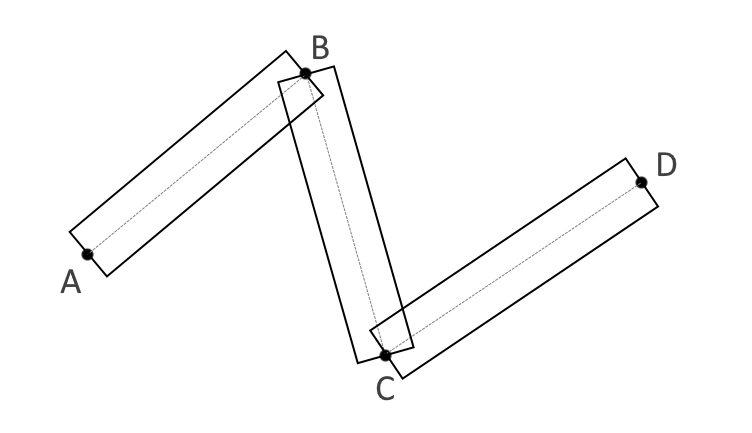
Чтобы избавиться от видимой сегментации в узловых точках, необходимо совместить смежные точки соседних сегментов, так чтобы сохранить толщину на обоих участках соседних сегментов. Для этого надо найти пересечение односторонних граней линии, сверху и снизу (рис. 2):
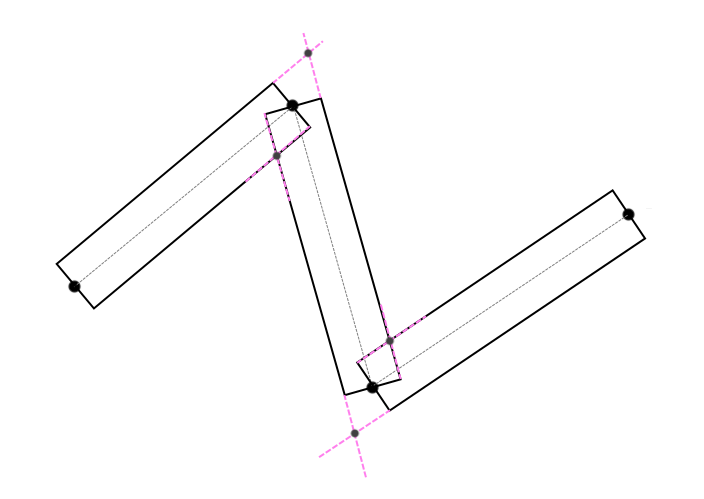
(рис. 2)
Однако угол между соседними сегментами, может быть настолько острым, что точка пересечения, может уйти далеко от точки соединения этих линий (рис. 3).
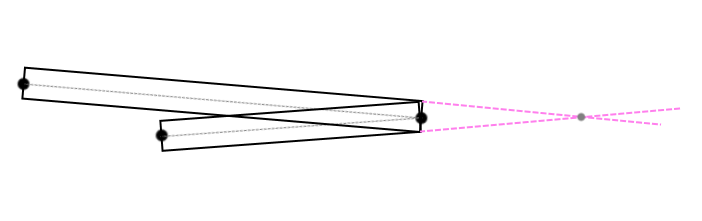
(рис. 3)
В таком случае этот угол необходимо как-то обработать (рис. 4):
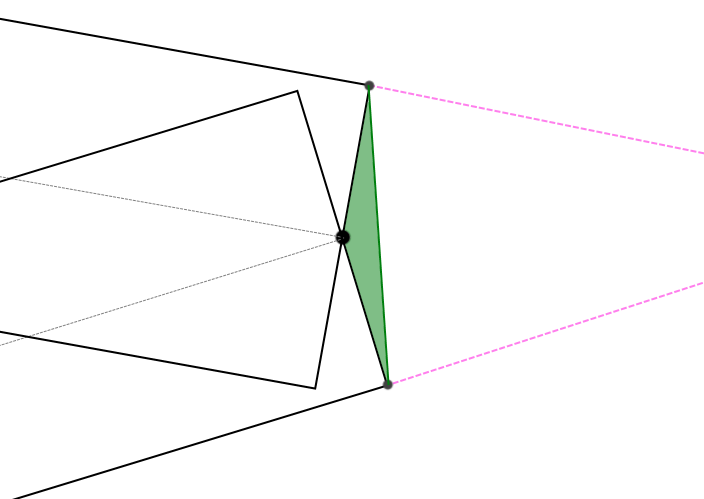
(рис. 4)
Я решил, заполнять такие области соответствующими треугольниками. Мне на помощь пришла последовательность GL_LINE_STRING, которая при правильном порядке, должна в случае слишком острого угла (пороговое значение проверяется в вершинном шейдере) создавать эффект аккуратно обрезанного угла (рис. 5), либо совмещать смежные координаты соседних сегментов по правилу пересечения односторонних граней (рис. 2), как раньше.
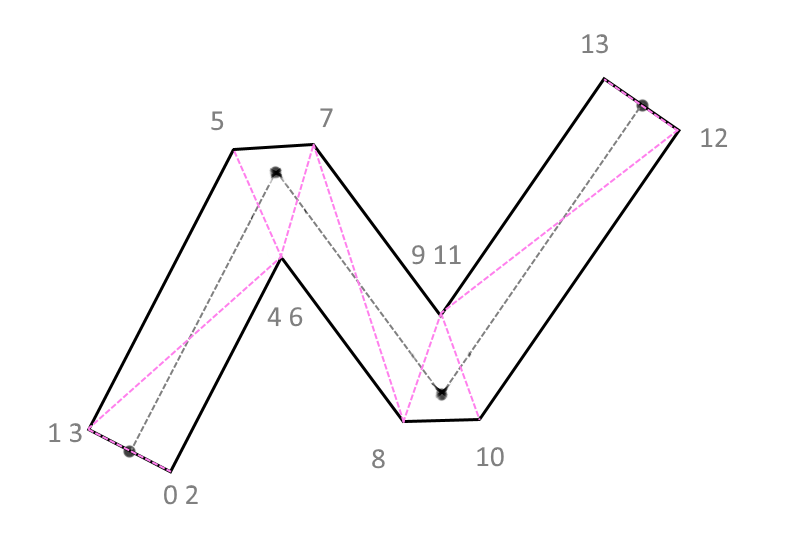
(рис. 5)
Числа возле вершин — это индексы вершин, по которым происходит отрисовка полигонов в графическом конвейере. Если угол тупой, в этом случае треугольник для обрезания сольется в бесконечно тонкую линию и станет невидимым (рис. 6).
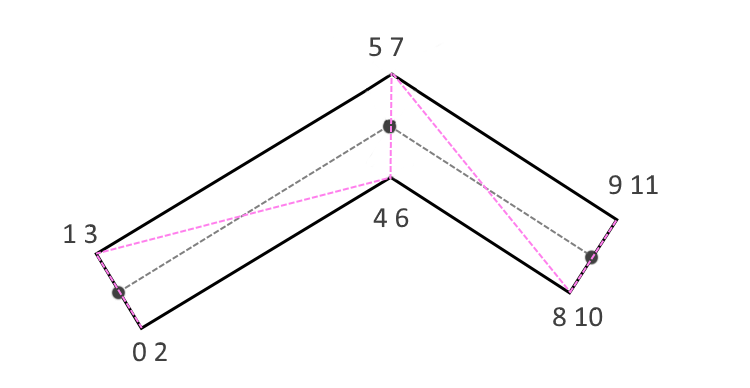(рис. 6)
Про себя представляем последовательность таким образом(рис. 7):
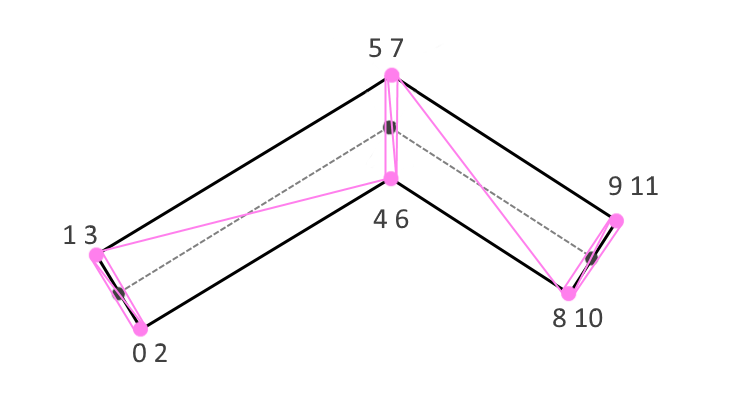
(рис. 7)
Вот и весь секрет. Теперь давайте посмотрим, как это рендерить. Необходимо создать буфер вершин, буфер индексов и буфер порядка, который показывает в каком направлении от текущей вершины сегмента делать утолщение, а также, какая часть сегмента в данный момент обрабатывается вершинным шейдером, начальная или конечная. Для того, чтобы находить пересечение граней, кроме координат текущей точки, нам также необходимо знать предыдущую и следующую координаты от нее (рис. 8).
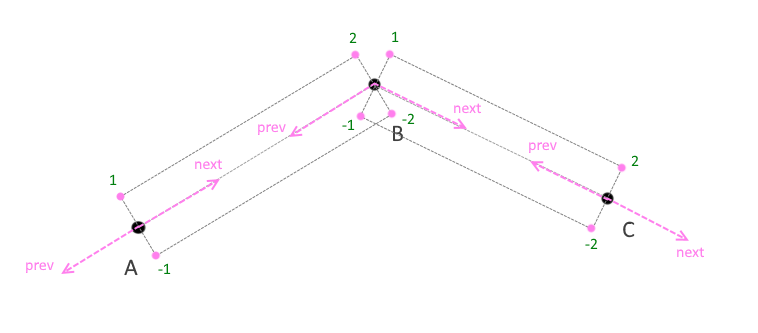
(рис. 8)
Итак, для каждой координаты в шейдере у нас должны быть, собственно, сама координата, предыдущая и следующая координаты, порядок точки т.е. является ли точка началом, или концом сегмента(я обозначаю -1, 1 — это начало и -2, 2 — конец сегмента), как должна она располагаться: сверху или снизу от текущей координаты, а также толщина и цвет.
Т.к. WebGL позволяет использовать один буфер для разных атрибутов, то в случае, если элементом этого буфера является координата, при вызове vertexAttribPointer каждому атрибуту назначается в байтах размер элемента буфера, и смещение относительно текущего элемента атрибута. Это хорошо видно, если изобразить последовательность на бумаге (рис. 9):
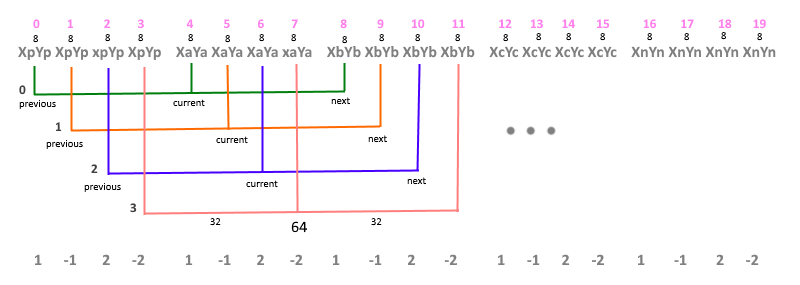
(рис 9)
Верхняя строчка — это индексы в массиве вершин; 8 — размер элемента (координата тип vec2) т.е. 2х4 байта; Xi, Yi — значения координат в точках А, B, C; Xp = Xa — Xb, Yp = Yа — Yb, Xn = Xc — Xb, Yn = Xc — Xb т.е. вершины указывающие направление в пограничных точках. Цветными дугами изображены связки координат (предыдущая, текущая и следующая) для каждого индекса в вершинном шейдере, где current — текущая координата связки, previous — предыдущая координата связки и next — следующая координата связки. Значение 32 байт — смещение в буфере для того, чтобы идентифицировать текущее(current) относительно предыдущего (previous) значения координат, 64 байт — смещение в буфере для идентификации следующего(next) значения. Т.к. индекс очередной координаты начинается с предыдущего (previous) значения, то для него смещение в массиве равно нулю. Последняя строчка показывает порядок каждой координаты в сегменте, 1 и -1 — это начало сегмента, 2 и -2 — соответственно, конец сегмента.
В коде это выглядит так:
var vb = this._verticesBuffer;
gl.bindBuffer(gl.ARRAY_BUFFER, vb);
gl.vertexAttribPointer(sha.prev._pName, vb.itemSize, gl.FLOAT, false, 8, 0);
gl.vertexAttribPointer(sha.current._pName, vb.itemSize, gl.FLOAT, false, 8, 32);
gl.vertexAttribPointer(sha.next._pName, vb.itemSize, gl.FLOAT, false, 8, 64);
gl.bindBuffer(gl.ARRAY_BUFFER, this._ordersBuffer);
gl.vertexAttribPointer(sha.order._pName, this._ordersBuffer.itemSize, gl.FLOAT, false, 4, 0);
Так выглядит функция, которая создает массивы вершин и порядков, где pathArr — массив массивов координат по которым заполняются массивы для инициализации буферов outVertices — массив координат, outOrders — массив порядков и outIndexes — массив индексов:
Polyline2d.createLineData = function (pathArr, outVertices, outOrders, outIndexes) {
var index = 0;
outIndexes.push(0, 0);
for ( var j = 0; j < pathArr.length; j++ ) {
path = pathArr[j];
var startIndex = index;
var last = [path[0][0] + path[0][0] - path[1][0], path[0][1] + path[0][1] - path[1][1]];
outVertices.push(last[0], last[1], last[0], last[1], last[0], last[1], last[0], last[1]);
outOrders.push(1, -1, 2, -2);
//На каждую вершину приходится по 4 элемента
for ( var i = 0; i < path.length; i++ ) {
var cur = path[i];
outVertices.push(cur[0], cur[1], cur[0], cur[1], cur[0], cur[1], cur[0], cur[1]);
outOrders.push(1, -1, 2, -2);
outIndexes.push(index++, index++, index++, index++);
}
var first = [path[path.length - 1][0] + path[path.length - 1][0] - path[path.length - 2][0], path[path.length - 1][1] + path[path.length - 1][1] - path[path.length - 2][1]];
outVertices.push(first[0], first[1], first[0], first[1], first[0], first[1], first[0], first[1]);
outOrders.push(1, -1, 2, -2);
outIndexes.push(index - 1, index - 1, index - 1, index - 1);
if ( j < pathArr.length - 1 ) {
index += 8;
outIndexes.push(index, index);
}
}
};
Пример:
var path = [[[-100, -50], [1, 2], [200, 15]]];
var vertices = [],
orders = [],
indexes = [];
Polyline2d.createLineData(path, vertices, orders, indexes);
Получим:
vertices: [-201, -102, -201, -102, -201, -102, -201, -102, -100, -50, -100, -50, -100, -50, -100, -50, 1, 2, 1, 2, 1, 2, 1, 2, 200, 15, 200, 15, 200, 15, 200, 15, 399, 28, 399, 28, 399, 28, 399, 28]
orders: [1, -1, 2, -2, 1, -1, 2, -2, 1, -1, 2, -2, 1, -1, 2, -2, 1, -1, 2, -2]
indexes: [0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 11, 11, 11]
Вершинный шейдер:
attribute vec2 prev; //предыдущая координата
attribute vec2 current; //текущая координата
attribute vec2 next; //следующая координата
attribute float order; //порядок
uniform float thickness; //толщина
uniform vec2 viewport; //размеры экрана
//Функция проецирование на экран
vec2 proj(vec2 coordinates){
return coordinates / viewport;
}
void main() {
vec2 _next = next;
vec2 _prev = prev;
//Блок проверок для случаев, когда координаты точек равны
if( prev == current ) {
if( next == current ){
_next = current + vec2(1.0, 0.0);
_prev = current - next;
} else {
_prev = current + normalize(current - next);
}
}
if( next == current ) {
_next = current + normalize(current - _prev);
}
vec2 sNext = _next,
sCurrent = current,
sPrev = _prev;
//Направляющие от текущей точки, до следующей и предыдущей координаты
vec2 dirNext = normalize(sNext - sCurrent);
vec2 dirPrev = normalize(sPrev - sCurrent);
float dotNP = dot(dirNext, dirPrev);
//Нормали относительно направляющих
vec2 normalNext = normalize(vec2(-dirNext.y, dirNext.x));
vec2 normalPrev = normalize(vec2(dirPrev.y, -dirPrev.x));
float d = thickness * 0.5 * sign(order);
vec2 m; //m - точка сопряжения, от которой зависит будет угол обрезанным или нет
if( dotNP >= 0.99991 ) {
m = sCurrent - normalPrev * d;
} else {
vec2 dir = normalPrev + normalNext;
// Таким образом ищется пересечение односторонних граней линии (рис. 2)
m = sCurrent + dir * d / (dirNext.x * dir.y - dirNext.y * dir.x);
//Проверка на пороговое значение остроты угла
if( dotNP > 0.5 && dot(dirNext + dirPrev, m - sCurrent) < 0.0 ) {
float occw = order * sign(dirNext.x * dirPrev.y - dirNext.y * dirPrev.x);
//Блок решения для правильного построения цепочки LINE_STRING
if( occw == -1.0 ) {
m = sCurrent + normalPrev * d;
} else if ( occw == 1.0 ) {
m = sCurrent + normalNext * d;
} else if ( occw == -2.0 ) {
m = sCurrent + normalNext * d;
} else if ( occw == 2.0 ) {
m = sCurrent + normalPrev * d;
}
//Проверка "внутренней" точки пересечения, чтобы она не убегала за границы сопряженных сегментов
} else if ( distance(sCurrent, m) > min(distance(sCurrent, sNext), distance(sCurrent, sPrev)) ) {
m = sCurrent + normalNext * d;
}
}
m = proj(m);
gl_Position = vec4(m.x, m.y, 0.0, 1.0);
}
Пару слов в заключении
Данный подход реализован для рисования треков, орбит, векторных данных.
В заключении хочу добавить несколько идей, что можно сделать с алгоритмом, чтобы улучшить качество линий. Например, можно передавать для каждой вершины цвет в атрибуте colors, тогда линия станет разноцветной. Так-же каждой вершине можно передавать ширину, тогда линия будет меняться по ширине от точки к точке, а если рассчитывать ширину в точке (в вершинном шейдере) относительно удаленности от точки наблюдения (для трехмерного случая), можно добиться эффекта, когда часть линии расположенная ближе к точке наблюдения визуально больше, чем та часть линии, которая находится на отдалении. Еще можно реализовать сглаживание (antialiasing), добавив два прохода для каждого из краев толстой линии, в которых происходит рисование тонких линий (рамка по краям) с небольшой прозрачностью относительно центральной части.
Автор: mgevlich
