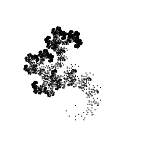
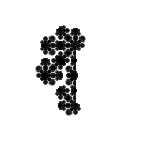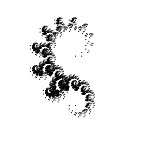Сегодня будем рисовать геометрические фракталы, которым уделяют незаслуженно мало внимания. А между тем, тут каждый фрактал — маленький шедевр, поражающий воображение!

Дальше много картинок и gif-анимация. Но прежде, чем переходить под кат, посмотрите на картинку выше и скажите, что на ней нарисовано?
Алгоритм
Рассмотрим один любопытный алгоритм на примере известного фрактала — кривой Леви.
Есть у нас две точки A1 и A2. Найдем такую точку A3, для которой угол A1 = 45°, а угол A3 = 90°.
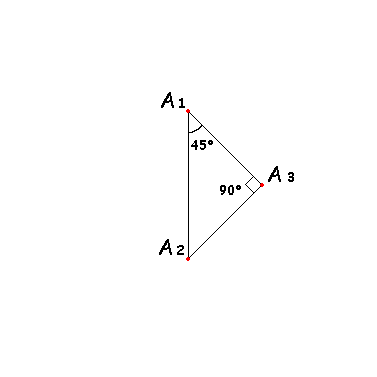
Проделаем ту же операцию для точек A1, A3 и A3, A2.
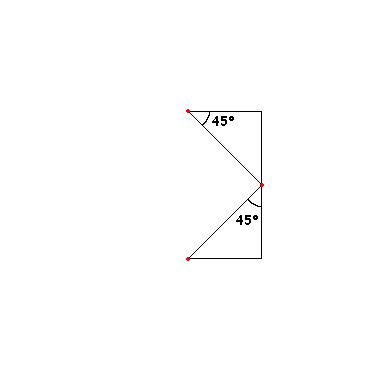
И дальше рекурсивно для каждой пары точек.
Третья итерация:
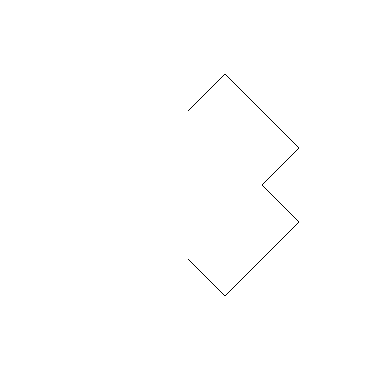
На 14 итерации эта кривая выглядит вот так:

Более наглядно на JavaScript:
<canvas id="myCanvas"></canvas>
<script>
window.onload=function(){
var canvas=document.getElementById('myCanvas');
var context=canvas.getContext('2d');
canvas.width=800, canvas.height=800;
context.beginPath();
recurs(context, 17, 400, 250, 400, 550); //рекурсивная функция, рисующая фрактальную кривую
context.stroke();
};
var angle=45*Math.PI/180; //переводим углы в радианы
function recurs(context, n, x0, y0, x1, y1){ //n итераций, Точки A1(x0,y0) и A2(x1,y1)
if (n==0){
context.moveTo(x0,y0);
context.lineTo(x1,y1);
}else{
var xx=Math.cos(angle)*((x1-x0)*Math.cos(angle)-(y1-y0)*Math.sin(angle))+x0;
var yy=Math.cos(angle)*((x1-x0)*Math.sin(angle)+(y1-y0)*Math.cos(angle))+y0; //находим точку A3
recurs(context, n-1, x0, y0, xx, yy); //A1, A3
recurs(context, n-1, xx, yy, x1, y1); //A3, A2
}
}
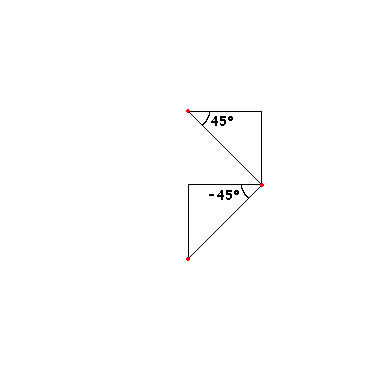
</script>Немного модифицировав приведенный выше код, можем нарисовать другую известную фрактальную кривую — Дракон Хартера-Хейтуэя. Для этого, начиная со второй итерации, будем чередовать углы 45° и -45°
Третья итерация:
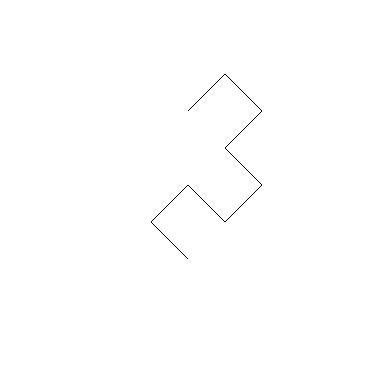
На 14 итерации эта кривая выглядит вот так:
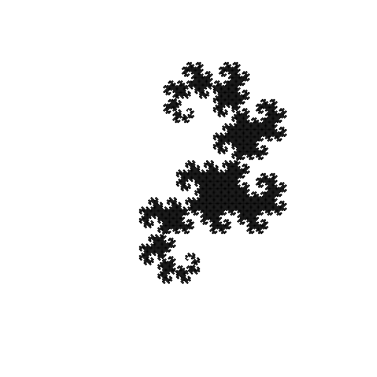
}else{
angle2=angle*k; // <-
var xx=Math.cos(angle2)*((x1-x0)*Math.cos(angle2)-(y1-y0)*Math.sin(angle2))+x0;
var yy=Math.cos(angle2)*((x1-x0)*Math.sin(angle2)+(y1-y0)*Math.cos(angle2))+y0;
recurs(context, n-1, x0, y0, xx, yy, 1); //последний аргумент функции - k
recurs(context, n-1, xx, yy, x1, y1, -1);
}Мы самую малость изменили нашу функцию, добавив в нее еще один угол, а фрактал изменился до неузнаваемости! В динамике (изменяем второй угол с шагом в 5°):
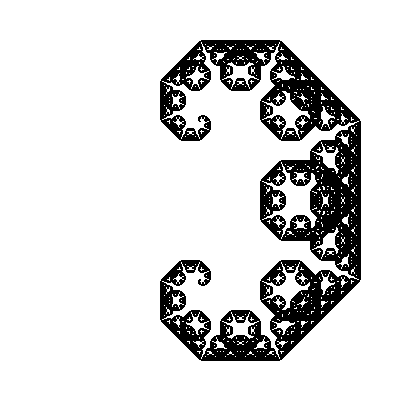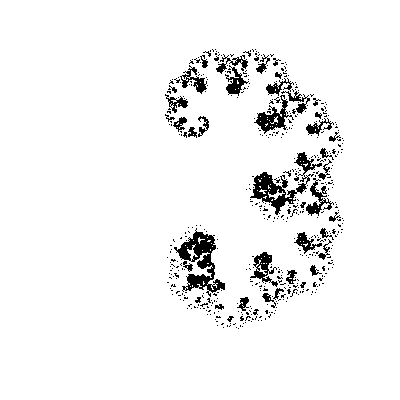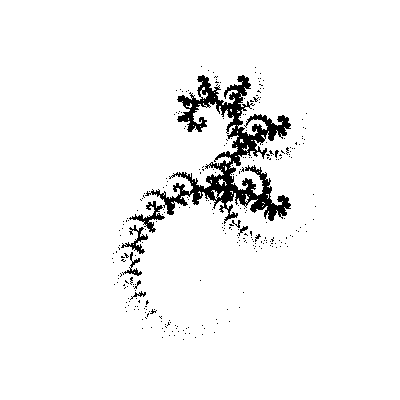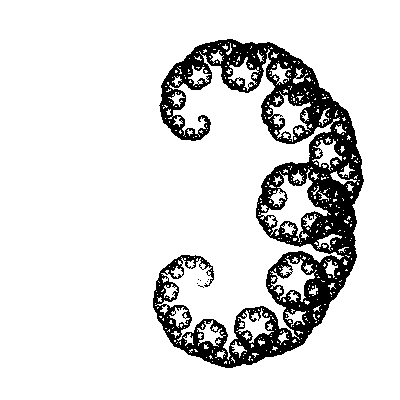
И вот тут наш пытливый ум начинает задавать вопросы. А что, если попробовать использовать другие значения углов, вместо [45,-45]? Скажем, [30,-60]. Или [30,-30,-60,60]. Перепишем нашу функцию, чтобы она принимала массив с углами, в качестве одного из аргументов.
function recurs(context, arr, position, n, x0, y0, x1, y1){
if (n==0){
context.fillRect(x1,y1, 1,1);
return position;
}else{
if (!position[n]) position[n]=0;
var xx=Math.cos(arr[position[n]])*((x1-x0)*Math.cos(arr[position[n]])-(y1-y0)*Math.sin(arr[position[n]]))+x0;
var yy=Math.cos(arr[position[n]])*((x1-x0)*Math.sin(arr[position[n]])+(y1-y0)*Math.cos(arr[position[n]]))+y0;
position[n]++;
if (position[n]==arr.length) position[n]=0;
position=recurs(context, arr, position, n-1, x0, y0, xx, yy);
position=recurs(context, arr, position, n-1, xx, yy, x1, y1);
return position;
}
}Массив position хранит номер угла из массива arr для текущей глубины рекурсии (n).
Запустить в браузере (Через запятую пишем значения углов в градусах, жмем «draw!»)
С этого момента будем рисовать только точки, не соединяя их линиями… чисто из эстетических соображений. Фрактал [30,-30,-60,60] нарисованный линиями и точками:
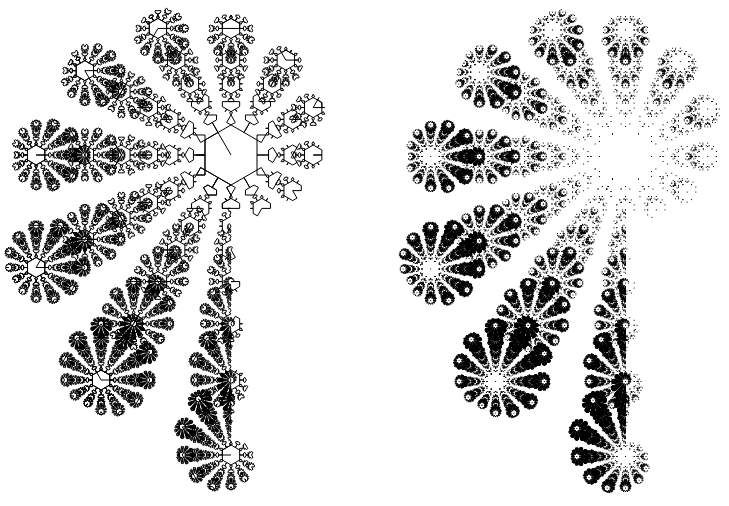
Особое внимание следует обратить на то, что все точки A3 лежат на окружности с диаметром A1A2:
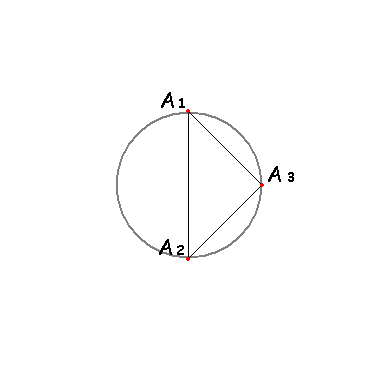
Если точки находятся внутри (или снаружи) окружности — фрактал получается слишком сжатым (или наоборот — выходит за пределы области отрисовки). Наглядно:

Вот этим косинусом мы выравниваем точки по окружности:
var xx=Math.cos(arr[position[n]])* ...
var yy=Math.cos(arr[position[n]])* ...Не трудно заметить, что используя угол 120° мы получим ту же точку, что и с углом -60°. Поэтому все углы лежат в диапазоне (-90°,90°).
Попробуем ввести в наш скрипт разные комбинации углов.
«Маленькие шедевры»
Несколько рандомных фракталов с углами -45°/45° (кликабельно):
С углами -30°/30°/-60°/60°:
С углами -15°/15°/-30°/30°/-45°/45°/-60°/60°/-75/75°:
… Так можно продолжать очень долго. Если использовать углы 15°/30°/45°/60°/75° (положительные и отрицательные) и, скажем, рисовать «восьмиугольные» фракталы — сколько всего фракталов мы сможем нарисовать? Примерно 10^8 = 100 000 000 штук. Кроме того, множество «восьмиугольных» фракталов не имеет пересечений с множеством, скажем, «девятиугольных» фракталов (за исключением фракталов, у которых все углы одинаковые). В общем, очень немало фракталов можно нарисовать этим алгоритмом.
Искать вручную что-то среди этого множества, при этом не зная, как это «что-то» должно выглядеть — немного затруднительно. Что мешает нам прикрутить сюда генетический алгоритм? Ничего. Прикрутим!
Эволюция
Генетический алгоритм — эвристический алгоритм поиска, использующий механизмы биологической эволюции. Алгоритм прост, интуитивно понятен и вместе с тем довольно эффективен.
Делится на несколько этапов.
- Создается начальная популяций, состоящая из небольшого числа особей. Каждая особь представляет из себя массив фиксированной длины с набором генов (генотип). Генотипы начальной популяции заполняются случайным образом. Применительно к нашей задаче, гены — это углы, с помощью которых будем рисовать фракталы.
- На следующем этапе происходит селекция. Для каждой особи считаем коэффициент приспособленности (fitness). Чем лучше особь — тем выше коэффициент. Сортируем популяцию по этому коэффициенту. Делим популяцию пополам — из наиболее приспособленных будем формировать следующую популяцию. (Как делить и что выбирать для следующей популяции — тема, на которую можно долго спорить)
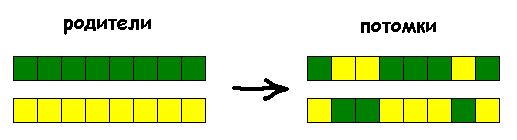
- Следующий этап — скрещивание. Из наиболее приспособленных выбираем (случайным образом) две особи — родителей. Делаем двух потомков: берем случайным образом часть генов одного родителя и часть генов другого, заполняем ими генотип одного из потомков. Оставшиеся гены уходят второму потомку. Берем следующих двух родителей. Проделываем ту же операцию. Так пока не закончатся родители. Из родителей и потомков формируем новую популяцию.
- Заключительный этап — мутации. Берем некоторый процент особей из новой популяции, для каждой из них (особей) выбираем случайным образом ген и заменяем его на случайное значение. Таким образом мы добавляем в наш генофонд гены, которых не было в начальной популяции и которые, в перспективе, могут сформировать наилучшие результаты. Кроме того, повышая процент мутаций, можно в какой-то степени решить проблему сходимости к локальному оптимуму.
Каждый этап более наглядно на JavaScript.
Начальная популяция
function randomangl(min, max, step){
if(step==0) step=1;
var rand=Math.floor(Math.random() * (max/step - min/step + 1)) + min/step;
if(rand==0) rand=1;
rand*=step;
if(rand>max) rand=max;
return Math.round(rand);
}
Функция randomangl вызывается с тремя аргументами: минимальный угол, максимальный угол и шаг. Удобно, если мы хотим заполнить начальную популяцию определенными углами. Например, можно вызвать функцию с следующими аргументами:
randomangl(-45, 45, 90) — сгенерирует углы -45°/45°
randomangl(-60, 60, 30) — сгенерирует углы -60°/-30°/30°/60°
randomangl(-75, 75, 15) — сгенерирует углы -75°/-60°/-45°/-30°/-15°/15°/30°/45°/60°/75°
Углы 0° не используем. Фрактал [45°,0°] выглядел бы вот так:
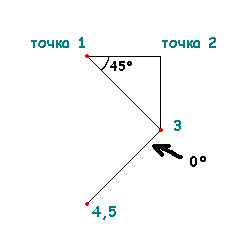
Получаем тот же фрактал [45°], только в том месте, где пытаемся нарисовать 0° — точки сливаются (вся дальнейшая рекурсия в этом месте становится бессмысленной). По этой же причине, нет смысла генерировать фракталы с использованием 90°. Для начальной популяции лучше всего вызвать функцию randomangl(-75, 75, 15). Для мутаций — randomangl(-89, 89, 1).
population=[];
fitness=[];
for(var n=anglemin; n<=anglemax; n++){
population[n]=[];
fitness[n]=[];
for(var i=0; i<PopulationSize; i++){
population[n][i]=[];
fitness[n][i]=0;
for(var j=0; j<n; j++){
population[n][i][j]=randomangl(min, max, step);
if(j==0) population[n][i][j]=Math.abs(population[n][i][j]);
}
}
}Создаем сразу несколько популяций с разным количеством углов (anglemin, anglemax). Инициализируем отдельный массив с коэффициентам приспособленности. Первый ген у каждой особи принудительно делаем положительным — фракталы [45°,-45°] и [-45°,45°] симметричны.
Селекция
Вообще, приспособленность каждой особи, в классических генетических алгоритмах, определяется специальной fitness-функцией. Функция оценивает, насколько каждая из особей решает поставленную задачу. В нашем случае, четко сформулировать задачу не представляется возможным (не знаем, как это «что-то» должно выглядеть), поэтому в качестве fitness-функции прикрутим к алгоритму пользователя.
Есть два варианта. Можно было бы нарисовать все фракталы из популяций и предложить пользователю отобрать самые лучшие, но могут возникнуть некоторые трудности — как выбрать лучшие фракталы, когда они все выглядят впечатляюще? Намного проще сравнивать два случайных фрактала.
Интерфейс:

На страничке два канваса: myCanvas1 и myCanvas2. И две кнопочки: onclick=«selecter(1);» и onclick=«selecter(2);»
Вызываем функцию, которая рисует два случайных фрактала:
function get2fractals(){
PopulationNumber=Math.floor(Math.random() * (anglemax - anglemin + 1))+anglemin;
drawcanvas(1);
drawcanvas(2);
}
function drawcanvas(n){
var canvas=document.getElementById('myCanvas'+n);
var context=canvas.getContext('2d');
canvas.width=canvasSize, canvas.height=canvasSize;
context.fillStyle = 'rgb(255,255,255)';
context.fillRect (0, 0, canvas.width, canvas.height);
var position=[];
if(n==1){
FractalNumber[1]=Math.floor(Math.random() * (PopulationSize));
}else{
do{
var rnd = Math.floor(Math.random() * (PopulationSize));
}while(rnd==FractalNumber[1])
FractalNumber[2]=rnd;
}
var array1fractal=population[PopulationNumber][FractalNumber[n]];
context.fillStyle = 'rgb(0,0,0)';
draw(context, array1fractal, position, iteration, xA, yA, xB, yB);
}
В функции get2fractals выбираем случайную популяцию.
В функции drawcanvas проверяем if(n==1) — чтобы не рисовать два одинаковых фрактала. Номер популяции и номера двух фракталов храним в глобальных переменных (PopulationNumber и FractalNumber[]).
Когда пользователь жмет на кнопку Select рядом с понравившимся ему фракталом, вызываем такую функцию:
function selecter(n){
fitness[PopulationNumber][FractalNumber[n]]++;
get2fractals();
}Которая повышает коэффициент приспособленности для выбранного фрактала и рисует два новых фрактала.
Будем считать, что пользователь оказался добросовестным и произвел выборов не меньше, чем количество особей в популяции, прежде чем запустить механизм эволюции.
Скрещивание и мутации
function sortf(a, b) {
if (a[1] < b[1]) return 1;
else if (a[1] > b[1]) return -1;
else return 0;
}
function evolution(){
var mutation=document.getElementById("mutatepercent").value;
var exchange=document.getElementById("exchangepercent").checked;
var sizehalf=PopulationSize/2;
var sizequarter=sizehalf/2;
for(var n=anglemin; n<=anglemax; n++){
var arrayt=[];
for(var i=0; i<PopulationSize; i++){
arrayt[i]=[];
arrayt[i][0]=population[n][i];
arrayt[i][1]=fitness[n][i];
}
arrayt.sort(sortf);
arrayt.length=sizehalf;
population[n].length=0;
fitness[n].length=0;
for(var i=0; i<sizequarter; i++){
var i0=i*4;
var i1=i*4+1;
var i2=i*4+2;
var i3=i*4+3;
var removed1=Math.floor(Math.random()*(arrayt.length));
var parent1f = arrayt.splice(removed1,1);
var parent1=parent1f[0][0];
var removed2=Math.floor(Math.random()*(arrayt.length));
var parent2f = arrayt.splice(removed2,1);
var parent2=parent2f[0][0];
var child1=[];
var child2=[];
for(var j=0; j<n; j++){
var gen=Math.round(Math.random());
if(gen==1){
child1[j]=parent1[j];
child2[j]=parent2[j];
}else{
child1[j]=parent2[j];
child2[j]=parent1[j];
}
}
population[n][i0]=parent1;
population[n][i1]=parent2;
population[n][i2]=child1;
population[n][i3]=child2;
fitness[n][i0]=0;
fitness[n][i1]=0;
fitness[n][i2]=0;
fitness[n][i3]=0;
}
if(mutation>0){
var m=100/mutation;
for(var i=0; i<PopulationSize; i++){
var rnd=Math.floor(Math.random()*(m))+1;
if(rnd==1){
var mutatedgene=Math.floor(Math.random()*(n));
population[n][i][mutatedgene]=randomangl(minm, maxm, stepm);
}
}
}
}
if(exchange){
///...
}
get2fractals();
}
Берем поочередно каждую популяцию. Пишем всех особей во временный массив, туда же пишем их коэффициенты приспособленности fitness. Сортируем временный массив по этим коэффициентам. Отрезаем половинку (самых приспособленных). Старые два массива обнуляем, чтобы там ничего лишнего не осталось. Дергаем из временного массива двух предков, формируем двух потомков. Заполняем популяцию предками и потомками.
Производим мутации. Небольшое замечание. Вместо процента мутаций во всей популяции, используем вероятность мутации отдельно взятой особи.
Доступна опция exchange. С помощью этой опции реализована модель миграции особей между популяциями.
if(exchange){
var n=anglemin;
while(n<population.length){
var rnd=Math.round(Math.random());
var np=n+1;
if(rnd==1 && (typeof population[np]!="undefined")){
var i1=Math.floor(Math.random() * (PopulationSize));
var i2=Math.floor(Math.random() * (PopulationSize));
var tempa1=population[np][i1];
var tempa2=population[n][i2];
var indexofexcessgene=Math.floor(Math.random()*(tempa1.length));
var excessgene=tempa1.splice(indexofexcessgene,1);
tempa2.splice(indexofexcessgene,0,excessgene[0]);
population[np][i1]=tempa2;
population[n][i2]=tempa1;
n+=2;
}else{
n++;
}
}
}Если флажок Exchanges установлен, поочередно для каждой популяции, одна случайная особь с вероятность 50% может обменяться генами со случайной особью из следующей популяции (популяция n+1). Генов в генотипах следующей популяции больше, обмен производим следующим образом. Выбираем случайный ген у особи в популяции n+1, вставляем его на ту же позицию в генотип у особи из популяции n. Меняем особи местами:
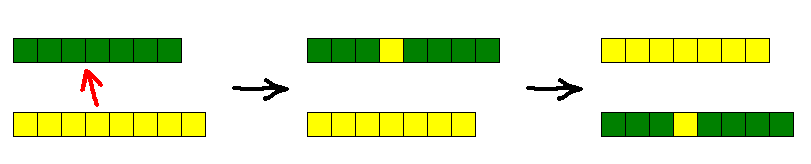
Осталось добавить свистелок (css-кнопочки, сохранение всего процесса в localStorage, отображение Parents Tree...)
Исходники можно посмотреть на GitHub
Или запустить в браузере, перейдя на сайт проекта (осторожно, можно залипнуть!)
Результат моих селекций — на картинке в начале публикации.
Ну и в заключение добавлю, что 2D — хорошо, а 3D — еще лучше!

Покрутить мышкой фрактал в трех измерениях можно здесь. Через слеш вбиваем пары углов /alpha/beta/alpa/beta/… в адресную строку
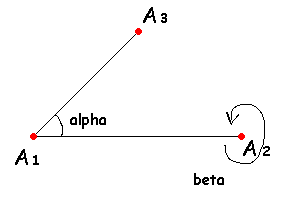
Alpha — уже привычный нам угол поворота. Новый угол Beta — поворот точки A3 вокруг оси A1A2.
3D алгоритмом можно нарисовать двумерные фракталы, которые не получится нарисовать 2D алгоритмом. Например:
45/0/45/180/45/180/45/180/45/0
45/180/45/180/45/0/45/180/45/180/

Небольшая галерея двумерных фракталов нарисованных этим алгоритмом.
Автор: xcont