Теория категорий на JavaScript. Часть 1. Категория множеств

Абстракция – это одна из основных техник в ИТ. Любой язык программирования или моделирования, любая парадигма программирования (процедурная, функциональная, ООП, …) дают ответ на вопрос, как и от чего нужно абстрагироваться. Причём, адепты каждого подхода предлагают какой-то свой вариант абстракции.

Если вы хотите увидеть истинную, универсальную абстракцию, то вступайте в нашу… изучайте теорию категорий. В статье на примере категории множеств с картинками и JavaScript-кодом объясняются самые базовые понятия теории категорий: пределы, универсальное свойство. Рассматривается вычислительный аспект теории категорий.

Также немного говорится про классы, примеси и смеси в JavaScript.

Примеры из статьи можно посмотреть тут.

Введение

Я думаю, что все слышали о теории категорий. Слышали, что это крутая silver-bullet теория, с помощью которой можно единообразно описывать очень разные вещи. Слышали, что она активно применяется в функциональных языках программирования. Кто-то возможно даже слышал о языках программирования или системах компьютерной алгебры, в значительной степени основанных на теории категорий.

В Интернете много книг и статей на эту тему. Но обычно они ориентированы либо на математиков, либо на ИТшников, занимающихся наукой и странными вещами типа Haskell, ML (ирония – не надо мне ставить минус в карму, как это обычно бывает после упоминания святого Haskell всуе).

А для простых работяг, которые каждый день зарабатывают себе на кусок хлеба фигаченьем на JavaScript, польза от теории категорий мало понятна. Я не обещаю, что после прочтения этого цикла статей она станет понятней. Но если всё получится, то возможно мы даже запилим приложение, которое будет делать что-то полезное.

Сразу предупреждаю, что у меня инженерное, а не математическое образование. Поэтому если вы ожидаете увидеть в статье строгие определения, доказательства теорем и т.п., то не увидите. Скорее наоборот, всё будет описываться «на пальцах». Если вы увидите какие-либо неточности, пожалуйста, пишите, я могу в чём-то ошибаться.

Что такое категория?

Категория – это всё что угодно, для чего определены:

• класс объектов,
• класс морфизмов (стрелочек) между объектами (причём, для каждого объекта существует тождественный морфизм),
• операция композиции морфизмов,
  • которая является ассоциативной:
    (h ∘ g) ∘ f = h ∘ (g ∘ f)
  • для которой тождественные морфизмы являются нейтральными элементами:
    f ∘ id_A = id_B ∘ f = f

Символ ∘ иногда опускают: (h g) f = h (g f)

Также вместо композиции иногда используют конкатенацию морфизмов, чтобы в формуле они шли в том же порядке, что и на диаграмме: (f ; g) ; h = f ; (g ; h) Но такая запись не так удобна как кажется, поэтому редко встречается. Если мы будем рассматривать элементы в следующих статьях, то вы в этом убедитесь.

Чтобы сконструировать категорию чего-то, необходимо

• придумать какие в этой категории будут объекты и морфизмы,
• не забыть про тождественные морфизмы,
• придумать, что представляет собой операция композиции морфизмов,
• доказать, что композиция обладает необходимыми свойствами,
• …
• profit.

Морфизмы должны иметь в точности один исходный и один целевой объект. Они не могут соединять 3 или более объектов, не могут «висеть в воздухе». (Категории высших порядков мы не рассматриваем.)

Применять операцию композиции можно только к совместимым морфизмам. Пусть есть морфизмы f : A → B, g : B → C и h : C → D. Композиция g ∘ f (или f; g) допустима. А следующие композиции недопустимы: h ∘ f, f ∘ f, f ∘ g.

Теперь рассмотрим пример категории. Представьте элементарный топос, он является категорией. Если представили, то вряд ли вы найдёте в этой статье для себя что-то новое. Лучше почитать что-нибудь более фундаментальное.

Пример свободной категории

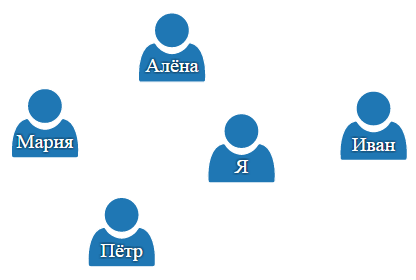
Если всё-таки продолжаете читать, то попробуем сконструировать более понятную категорию. Представьте вашу страницу вконтакте, а также страницы ваших друзей, подписчиков и тех, на кого вы подписаны – всех, с кем вы непосредственно связаны. Это будет класс объектов:

Для всех, на кого вы подписаны, нарисуйте стрелку от вашей страницы к странице этого человека. Для всех, кто подписан на вас, нарисуйте стрелку от их страниц к вашей. А для всех ваших друзей нарисуйте стрелки в обоих направлениях:

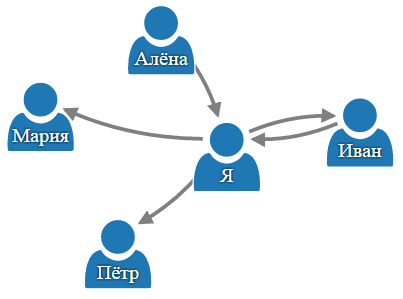
Теперь проделайте то же самое для остальных страниц:

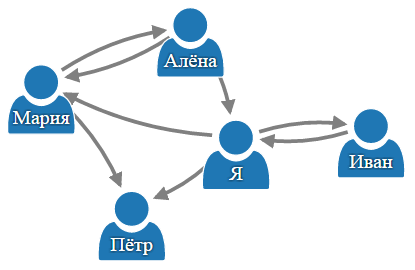
Будем считать, что если один человек подписан на другого, то 1-ый знает 2-го. Если два человека подписаны друг на друга (они друзья), то они знают друг друга. Т.е. морфизм в нашей категории – это отношение «знает».

Будем считать, что все знают сами себя и нарисуем тождественные морфизмы:

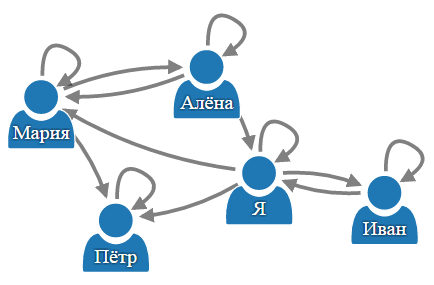
Определим операцию композиции морфизмов следующим образом.

Пусть f – это морфизм, обозначающий, что A знает B, а g – это морфизм, обозначающий, что B знает C. Тогда g ∘ f – это морфизм, который обозначает, что A опосредованно знает C.

Таким образом, класс морфизмов в нашей категории включает в себя не только отношение «знает», но и «опосредованно знает».

Ассоциативность операции композиции очевидна. Если А знает B, который знает C, который знает D, то как не группируй тут морфизмы, всё равно A опосредованно знает D.

То, что тождественные морфизмы являются нейтральными элементами композиции тоже очевидно. Если A знает B, то то, что они знают сами себя, ничего не меняет.

Мы построили свободную категорию. С одной стороны, этот пример показывает, как из чего угодно можно построить категорию. С другой стороны, показывает, что категории строятся по определённым правилам.

Пример предпорядка

В предыдущем примере объекты и морфизмы относительно простые, мы считаем, что у них отсутствует внутренняя структура.

Теперь представьте, что все страницы (ваша и людей, с которыми вы связаны) – это один объект. Множество страниц, имеющих отношение к другому человеку – это другой объект и так далее:

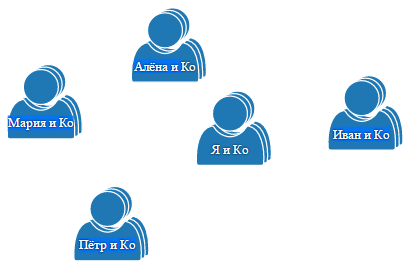
Какие морфизмы могут быть в такой категории?

Например, отношение «подмножество». Если каждый друг, подписчик и т.п. человека A является также другом подписчиком и т.п. человека B, то рисуем морфизм от A к B. В этом случае мы получим предпорядок, который является категорией:

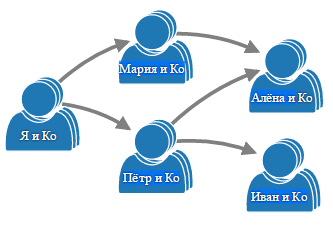
Или, например, в качестве морфизмов можем использовать функции, которые в качестве аргументов принимают страницы и возвращают для них некоторые другие страницы. В этом случае мы получим категорию множеств. Точнее, её подкатегорию, потому что категория множеств содержит все множества, а не только множества страниц вконтакте.

Коммутативные диаграммы

В рассмотренных примерах я отождествлял диаграммы с категориями. Но, вообще, это разные вещи. Строго говоря, диаграмма – это функтор. Что такое функтор нам пока неважно.

В одной из предыдущих статей мы уже отмечали, что модель и её представление в некоторой нотации (диаграмма, текстовое представление или ещё какое-то) – это разные вещи. Аналогично и с категориями.

Пока будем считать, что диаграмма – это некое визуальное представление фрагмента категории, в котором объекты изображаются в виде узлов, а морфизмы – в виде стрелочек между узлами. Впрочем, на диаграмме иногда можно изобразить всю категорию целиком, а не только её фрагмент. Бывают категории, содержащие всего один или несколько объектов и морфизмов.

Диаграммы могут быть коммутативными или некоммутативными.

Коммутативная диаграмма – это диаграмма, на которой для любой пары объектов результат композиции морфизмов не зависит от выбора направленного пути между этими объектами.

Лично я не сразу понял, как диаграмма может быть некоммутативной. Посмотрите на примеры свободной категории и предпорядка выше. Если между двумя объектами есть несколько путей, то явно все эти пути эквивалентные – они начинаются одним объектом и заканчиваются одним объектом. Как эти пути могут быть неэквивалентными?

Дело в том, что в данных категориях от некоторого объекта A к некоторому объекту B может идти максимум один морфизм. А, например, в категории множеств между одной и той же парой объектов может быть несколько совершенно разных морфизмов. Рассмотрим в качестве примера очень простую диаграмму с двумя объектами и двумя параллельными морфизмами. Коммутативна ли она?

Она будет коммутативна тогда и только тогда, когда выполняется равенство f = g. Вообще, в теории категорий коммутативные диаграммы часто используются как альтернатива записи систем уравнений. Можно написать «следующие равенства выполняются» и перечислить их. А можно написать «следующая диаграмма коммутативна» и нарисовать диаграмму, соответствующую системе уравнений.

Коммутативность данной диаграммы зависит от того какие множества и функции стоят за нарисованными объектами и морфизмами. Пусть объект A – это множество чисел, объект B – это множество геометрических фигур, морфизм f – это функция, которая для некоторого числа возвращает круг с радиусом равным этому числу, морфизм g – это функция, которая для некоторого числа возвращает квадрат с длиной стороны равной этому числу. Очевидно, что эти две функции не равны, а, значит, диаграмма некоммутативна:

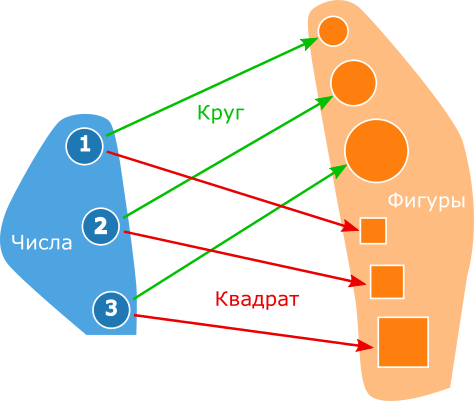
Пусть вас не смущает, что в одной категории смешиваются множества чисел и множества фигур. В этой же категории могут быть множества страничек вконтакте, множества множеств, графов, котиков и чего угодно – всё это одна категория множеств. Рассмотрим её более детально, но сначала немного общих сведений об исходном коде.

Общая информация по исходному коду

Исходные коды доступны тут, а примеры из статьи тут.

Сразу предупреждаю, что большую часть кода я писал 3 года назад, когда ещё не было ES6, и в стандартной библиотеке не было нормальных коллекций. Мне пришлось тогда реализовать свой Set. И, в целом, код наверняка организован не очень оптимально. Я, честно, пытался разложить всё по модулям, прочитал статью и понял, что теория категорий выглядит гораздо проще, чем вся эта жесть.

В файле Helpers.js наряду с другими вспомогательными функциями определены функции extend и combine. Функция extend уже давно придумана, она позволяет унаследовать один класс от другого и подробно описана тут. Единственное, моя реализация может добавлять в класс примеси. Очень рекомендую прочитать эту статью про примеси, где они рассматриваются как фабрики подклассов, описывается как их можно компактно описывать на ES6. Вообще, взгляд на примеси как на более общий случай наследования, при котором неизвестен заранее суперкласс, достаточно интересен.

Лично я не хочу заморачиваться с Babel и т.п., поэтому исходные коды написаны на ES5 и понадобились две эти функции. Примеси нельзя наследовать как классы с помощью extend, их можно только смешивать с помощью метода combine.

В файле Category.js определен абстрактный класс «категория», от которого должны наследоваться специфические категории. Также в нём определены примеси «полная категория» и «кополная категория» и их смесь «биполная категория». Категория множеств, которую мы будем рассматривать далее, как-раз является биполной категорией и к ней «примешиваются» некоторые универсальные алгоритмы, которые могут использоваться в любой биполной категории. Они реализованы именно в виде примесей, потому что JavaScript не поддерживает множественное наследование. Далее всё это объясняется подробнее.

В файле Set.js определена 1) категория множеств, 2) сами множества, 3) функции и 4) некоторые пределы категории множеств. Теоретически класс Set можно заменить на Set из ES6. Функции реализованы в виде так называемых графиков, т.е. в них в явном виде хранятся:

• допустимое множество входных элементов – домен (область определения);
• допустимое множество результирующих элементов – кодомен (область значений);
• множество пар: входной элемент и соответствующий ему результирующий элемент.

Домен и кодомен хранятся в явном виде, чтобы можно было проверять допустима ли композиция двух функций. Она допустима только если домен 1-ой функции совпадает с кодоменом 2-ой. Также домен используется при проверке того действительно ли функция является полной или это частично определенная функция. Если вы посмотрите код, там очень много подобных проверок (вызовы assert).

Наверное, возможно хранить функции именно в виде функций, а не их графиков, но это пока не принципиально.

В файле SetCategoryView.js рисовалка диаграмм для категории множеств, основанная на d3. Почти все иллюстрации в статье нарисованы с её помощью. К слову, в 4-ой версии d3 усовершенствовали Force Layout, теперь там можно самостоятельно определять произвольные силы. Усовершенствовали drag'n'drop, если я не ошибаюсь, то раньше он работал только для svg, а сейчас легко поддерживается и для canvas. В этой рисовалке вы теоретически можете найти что-то интересное, но она требует полного рефакторинга.

В файле Set.html все примеры из данной статьи.

Реализация категории множеств

Далее я буду описывать различные конструкции из категории множеств и как они реализуются в коде. Сама она реализована в виде следующей фабрики:

function SetCategory() { }
extend(SetCategory, Category, BicompleteCategory);

SetCategory.prototype.object = function (elements) {
  return new Set(elements);
};
SetCategory.prototype.morphism = function (A, B, mapping) {
  return new TotalFunction(A, B, mapping);
};
SetCategory.prototype.id = function (A) {
  return this.morphism(A, A).initId();
};
SetCategory.prototype.compose = function (g, f) {
  return g.compose(f);
};

Категория множеств наследуется от абстрактной категории и к ней примешивается поведение биполной категории.

Данная фабрика позволяет создавать

• объекты (которые являются множествами);
• морфизмы (которые являются функциями, отображающими элементы некоторого множества A на элементы некоторого множества B);
• тождественные морфизмы (которые являются тождественными отображениями некоторого множества A на себя);
• композиции двух морфизмов.

Честно говоря, я не сразу осознал почему категории должны быть фабриками. Скажем, множества, списки, стеки, деревья, графы и другие структуры обычно в явном виде хранят все свои элементы. Категории – это вроде аналогичные математические структуры, но почему они реализуются иначе? Почему нельзя реализовать категорию как хранилище её объектов и морфизмов? Потому, что в общем случае категория содержит бесконечное количество объектов и морфизмов. Причём, из них нам нужны всего лишь несколько. И их нужно не столько хранить, сколько конструировать на их основе новые объекты и морфизмы.

Создадим несколько объектов и морфизмов:

var setCat = new SetCategory();
var obj123 = setCat.object([1,2,3]);
var objAB = setCat.object(['a','b']);
var objABCD = setCat.object(['a','b','c','d']);
var f = setCat.morphism(obj123, objABCD, {1: 'c', 2: 'c', 3: 'd'});
var g = setCat.morphism(objABCD, objAB, {'a': 'a', 'b': 'b'});
var h = setCat.morphism(objAB, obj123, {'a': 1, 'b': 1});
showSetCategoryView('diagram1', setCat, {'A': obj123, 'B': objABCD, 'C': objAB},
  {'f': {dom: 'A', codom: 'B', morphism: f},
   'g': {dom: 'B', codom: 'C', morphism: g},
   'h': {dom: 'C', codom: 'A', morphism: h}});

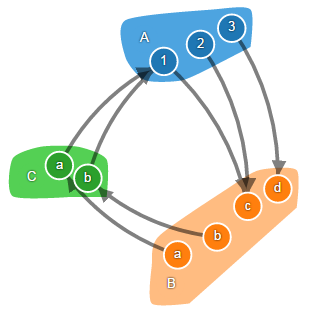
Жаль, что нельзя вставлять в статью выполняемый JavaScript код. Поэтому придётся вставлять картинки, но повторюсь, что подвигать всё это можно тут.

Эпиморфизм, мономорфизм, изоморфизм

Ок, мы умеем создавать объекты, морфизмы и красиво их рисовать. Что дальше?

Объекты и морфизмы могут обладать различными свойствами и значительная часть теории категорий посвящена описанию и изучению этих свойств. Наша реализация теории категорий должна уметь проверять эти свойства и должна уметь конструировать объекты и морфизмы с определенными свойствами. Начнём с самых простых свойств.

Напомню, что морфизмы в категории множеств – это функции. Из школы вы наверняка помните, что функции могут быть сюръекциями, инъекциями, биекциями. Я обещал, что не будет строгих определений и всё будет объясняться на пальцах, поэтому получайте:

Сюръекция – это функция, которая принимает все значения из своей области значений. Скажем, функция возведения в квадрат, определенная на множестве целых чисел, не является сюръекцией, потому что она не принимает значения 2, 3, 5, …

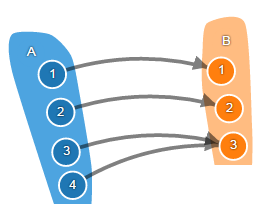
Инъекция – это функция, которая отображает разные элементы исходного множества в разные элементы результирующего множества. При этом область значений функции может содержать некоторые дополнительные элементы, у которых нет прообраза в области определения.

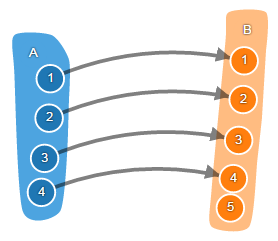
Биекция – это отображение один-к-одному. Функция является биекцией тогда и только тогда, когда она является одновременно сюръекцией и инъекцией.

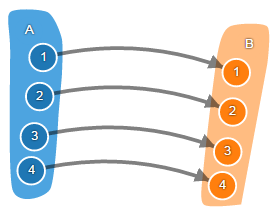
Для других математических объектов (например, графов) существуют некие аналоги сюръекций, инъекций и биекций. Поэтому в теории категорий, раз эта теория обо всём, решили эти понятия обобщить и ввели соответственно эпиморфизмы, мономорфизмы и изоморфизмы.

В чём же заключается это обобщение? В том, что в теории категорий мы полностью абстрагируемся от внутреннего устройства объектов и морфизмов. Вместо того, чтобы определять эти виды морфизмов через кружочки и стрелочки, как это сделано на рисунках выше, они определены через соотношения с другими морфизмами.

Эпиморфизм – это морфизм e : A → B, такой что из всякого равенства f ∘ e = g ∘ e следует f = g (другими словами, на e можно сокращать справа).

Чтобы было понятно о чём идёт речь, приведу пример НЕ эпиморфизма:

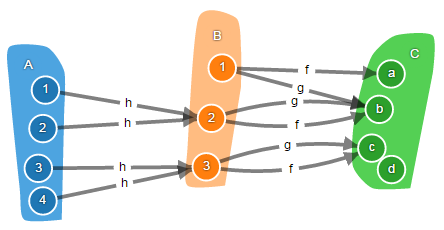
Диаграмма выше коммутативна (f ∘ h = g ∘ h). Чтобы в этом убедиться, вы можете пройти по стрелочкам от каждого элемента множества A и, независимо от выбранного пути, вы всегда придёте к одному и тому же элементу множества C. Т.е. функции f ∘ h и g ∘ h для одинаковых аргументов возвращают одинаковые результаты. Но(!) из этого не следует равенство функций f и g. Для элемента «1» они возвращают разные значения: «a» и «b». А, вот, если бы функция h была эпиморфизмом, то из коммутативности диаграммы следовало бы равенство f и g.

Далее я не буду так подробно описывать «переходы по стрелочкам через кружочки», просто имейте в виду, что, когда в категории множеств идёт речь о коммутативных диаграммах, вы всегда можете проверить эту коммутативность таким способом.

Ещё раз отмечу, что мы описали сюръективные функции только через соотношение с другими функциями, полностью абстрагируясь от деталей их внутреннего устройства. В этом суть теории категорий.

Мономорфизм – это морфизм m : A → B, такой что из всякого равенства m ∘ f = m ∘ g следует f = g (другими словами, на m можно сокращать слева).

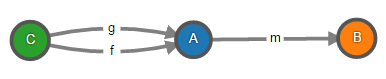
Изоморфизм – это морфизм f : A → B, для которого существует обратный, т.е. существует морфизм g : B → A, такой что f ∘ g = id_B и g ∘ f = id_A.

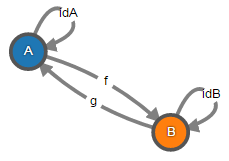
Вот, тут небольшой сюрприз. Не во всех категориях из того, что морфизм является эпиморфизмом и мономорфизмом следует, что он также является и изоморфизмом. Это демонстрирует то, что категория множеств конечно хороша для визуализации каких-то понятий, но может приводить к ложным аналогиям.

Конечный, начальный и нулевой объект

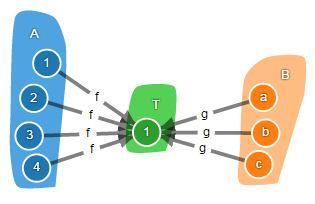
Конечный объект – это объект T, такой что для любого объекта X существует единственный морфизм u : X → T.

В категории множеств конечный объект – это синглетон, а уникальный морфизм – это функция, отображающая любой элемент исходного множества в единственный элемент синглетона. Терминальных объектов в категории множеств бесконечное количество, однако, все они изоморфны друг другу. Это значит, что с точки зрения теории категорий неважно о каком именно синглетоне идёт речь, всё, что верно для одного с точностью до изоморфизма будет верно и для любого другого синглетона.

Начальный объект – это объект I, такой что для любого объекта X существует единственный морфизм u : I → X.

В категории множеств начальный объект – это пустое множество, а уникальный морфзим, определённый на пустом множестве – это пустая функция. Причём, существует единственное пустое множество, соответственно, в категории множеств единственный начальный объект.

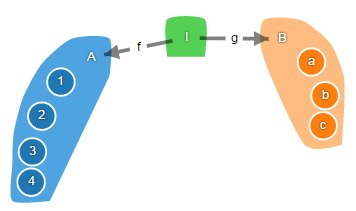
Нулевой объект – это объект, который является одновременно начальным и конечным объектом.

В категории множеств нулевых объектов нет, т.к. множество не может одновременно быть пустым и быть синглетоном.

Отметим несколько важных моментов.

Начальные и конечные объекты – это дуальные понятия, они эквивалентны с точностью до обращения направления морфизмов. Начальный объект будет конечным объектом в двойственной категории (категории с такими же объектами и операцией композиции, но морфизмами, направленными в обратном направлении). Идея дуальности или двойственности очень важна в теории категорий. Далее вы увидите ещё несколько примеров двойственных понятий.

К слову, конечные объекты можно называть коначальными, а начальные – коконечными, но тут мы уже попадаем в область одного фундаментально нового языка программирования. Если добавить или убрать у понятия приставку «ко-», то получим дуальное понятие. Кококонечные объекты я не встречал, хотя специалист по теории категорий должен понять, что речь идёт о начальных объектах.

В определениях выше ничего не говорится о морфизмах, направленных от конечного объекта. А они существуют. Например, некий морфизм f : {1} → {1,2,3,4} с графиком {(1,1)} или морфизм g с такой же сигнатурой, но графиком {(1,2)}. Т.е. они мало того, что существуют, но ещё и не уникальны и, забегая вперёд, играют достаточно важную роль. Поэтому представление о конечных объектах как об объектах, морфизмы которых направлены только к ним, не верно.

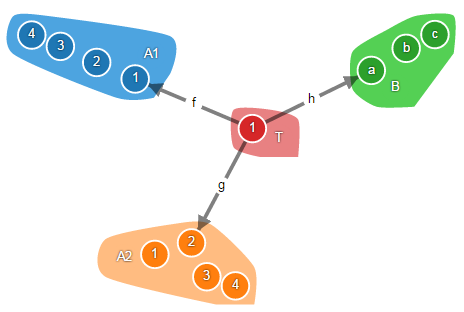
Насчёт морфизмов, направленных к начальным объектам, не могу ничего сказать. Я предполагаю, что в категории множеств их либо нет, либо это пустые уникальные функции. В принципе, почему бы им и не быть. Но тогда, каждое множество будет изоморфно пустому множеству. Если кто-то может прояснить этот момент, было бы отлично.

Универсальное свойство и самый важный момент

Обратите внимание на фразу «… существует единственный морфизм …» в определениях выше. Она повсеместно встречается в работах по теории категорий. Это называется «универсальное свойство».

Универсальное свойство позволяет определить понятие, абстрагируясь от деталей. Вы видите, что начальный и конечный объекты определены без упоминания пустых множеств, синглетонов, да, и, вообще, каких-либо структур. Вот, это настоящая абстракция! Я думаю, что в руководствах по теории категорий для разработчиков нужно говорить в первую очередь именно о таких вещах, а не о декартово замкнутых категориях или монадах.

Иными словами, в теории категорий вы определяете объекты, делая акцент не на описании их внутренней реализации, а на описании их внешнего поведения, того как они могут «взаимодействовать» с другими объектами, фактически вы описываете их интерфейс. Правда, немного иначе, чем это обычно делается в языках программирования, но этим теория категорий и интересна.

Вследствие абстрагирования от деталей универсальное свойство определяет объект с точностью до изоморфизма. Выше мы уже отмечали, что в категории множеств все конечные объекты (синглетоны) изоморфны. Но это верно для любых объектов, определенных через универсальное свойство. В принципе, это вполне логично: если два объекта внешне «ведут себя» одинаково (для них выполняется одно универсальное свойство), значит они изоморфны.

И, наверное, самый важный момент, который лежит в основе всего этого цикла статей. За универсальными свойствами обычно стоит некоторая оптимизационная задача, заключающаяся в поиске наилучших в некотором смысле объектов или морфизмов. Мы вернёмся к этому в разделе про уравнители.

Реализация конечных и начальных объектов

SetCategory.prototype.terminal = function () {
  return new SetTerminalObject(this).calculate();
};
function SetTerminalObject(cat) {
  this.cat = function () { return cat; };
}
SetTerminalObject.prototype.calculate = function () {
  this.obj = new Set([1]);
  return this;
}
SetTerminalObject.prototype.univ = function (A) {
  var mapping = {};
  A.forEach(function (el) {
    mapping[el] = 1;
  });
  return this.cat().morphism(A, this.obj, mapping);
}

SetCategory.prototype.initial = function () {
  return new SetInitialObject(this).calculate();
};
function SetInitialObject(cat) {
  this.cat = function () { return cat; };
}
SetInitialObject.prototype.calculate = function () {
  this.obj = new Set();
  return this;
}
SetInitialObject.prototype.univ = function (A) {
  return this.cat().morphism(this.obj, A, {});
}

У вас, возможно, возник вопрос: зачем столько кода для реализации синглетона и ПУСТОГО множества???

Конечный и начальный объекты – это не просто какие-то множества. Для них ещё должно выполняться универсальное свойство, которое имеет не какой-то теоретический характер, но оно активно используется в вычислениях. Например, при вычислении дополнения к кодекартову квадрату вычисляется универсальный морфизм для суммы объектов. Мы вернёмся к этому позже.

В нашей реализации у конструкций, обладающих универсальным свойством, будут методы:

• calculate – создаёт некоторую универсальную конструкцию или собирает её из других конструкций,
• complement – создаёт универсальную конструкцию из не очень типичных компонентов,
• univ – вычисляет для данной конструкции универсальные морфизмы.

Произведение

Продолжим нестрогие определения на пальцах и рассмотрим чуть более сложные объекты.

Произведение объектов X_j – это объект X и морфизмы π_j : X → X_j, называемые каноническими проекциями, такие что для любого объекта Y и морфизмов f_j : Y → X_j существует единственный морфизм u : Y → X, такой что π_j ∘ u = f_j.

В теории категорий вместо написания равенств вида π_j ∘ u = f_j можно нарисовать подобную диаграмму и сказать, что она коммутативна (пример для двух объектов, но в общем случае их может быть больше):

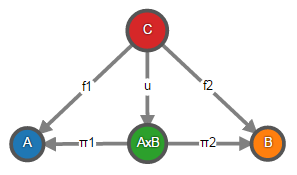
В категории множеств произведение объектов – это декартово произведение множеств.

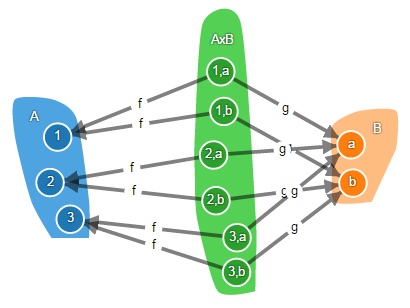
На рисунке произведение обозначено как AxB, а его элементы – как пары элементов из исходных множеств. Но это сделано для наглядности и совершенно не обязательно! Произведение можно назвать как угодно, а его элементами могут быть

• 1, 2, 3, …
• квадратик, кружочек, треугольничек, …
• или что угодно.

Произведение определено не как множество пар значений, а через соотношения между морфизмами. Сравните определения декартова произведения множеств и произведения объектов в теории категорий – они не имеют ничего общего. Вы снова видите пример абстрагирования от деталей в теории категорий.

SetCategory.prototype.product = function (A, B) {
  return new SetProduct(this).calculate(A, B);
};
function SetProduct(cat) {
  this.cat = function () { return cat; };
}
SetProduct.prototype.calculate = function (A, B) {
  var obj = new Set();
  var mapping1 = {};
  var mapping2 = {};
  A.forEach(function (x) {
    B.forEach(function (y) {
      var z = [x, y].toString();
      obj.add(z);
      mapping1[z] = x;
      mapping2[z] = y;
    });
  });
  this.obj = obj;
  this.f = this.cat().morphism(this.obj, A, mapping1);
  this.g = this.cat().morphism(this.obj, B, mapping2);
  return this;
};
SetProduct.prototype.univ = function(m, n) {
  assertEqualDom(m, n);
  assertEqualCodom(this.f, m);
  assertEqualCodom(this.g, n);
  var obj = m.dom();
  var mapping = {};
  obj.forEach(function (x) {
    var s1 = this.f.preimage(m.image(x));
    var s2 = this.g.preimage(n.image(x));
    mapping[x] = s1.intersection(s2).representative();
  }.bind(this));
  var u = this.cat().morphism(obj, this.obj, mapping);
  assertCommutes(this.f.compose(u), m);
  assertCommutes(this.g.compose(u), n);
  return u;
};

Обратите внимание, что в функции calculate вычисляется не только декартово произведение множеств, но и два морфизма – канонические проекции произведения на исходные объекты. В большинстве вычислений именно они играют основную роль и, грубо говоря, они гораздо важнее множества.

Функция univ вычисляет универсальный морфизм (u – на диаграмме выше) для некоторого объекта и пары морфизмов. Посмотрим, чем может быть полезен универсальный морфизм произведения.

На следующей диаграмме вы видите объекты A и B, их произведение AxB, а также некоторый произвольный объект C с морфизмами f₁ и f₂.

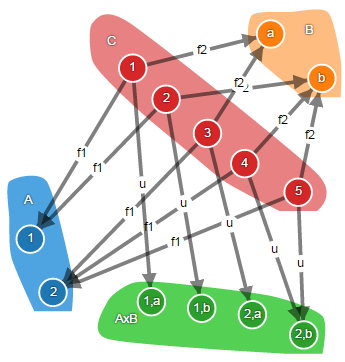
Вы видите, что элемент «1» множества C отображается на элемент «1» множества A и на элемент «a» множества B. Точно также как элемент «1,a» множества AxB. При вычислении универсального морфизма мы устанавливаем этот факт и конструируем универсальный морфизм таким образом, чтобы он отображал элемент «1» множества C на элемент «1,a» множества AxB.

Элементы «4» и «5» множества C отображаются морфизмами f₁ и f₂ на одни и те же элементы. Поэтому универсальный морфизм отображает их на один элемент «2,b» множества AxB.

Для наглядности представим, что C – это множество обезьянок. f₁ каждую обезьянку относит к одной из категорий: красивая или некрасивая, а f₂ – к одной из категорий: умная или глупая. Тогда универсальный морфизм u относит каждую обезьянку к одной из четырех категорий: красивая и умная, красивая и глупая, некрасивая и умная, некрасивая и глупая.

Фактически, универсальный морфизм для произведения – это произведение морфизмов.

Произведение в разном виде реализовано в различных языках программирования. Это и структуры, и кортежи, и всяческие join’ы в SQL, LINQ и т.п. Почитайте про типы-произведения.

В JavaScript канонические проекции произведения можно рассматривать как деструкторы или акцессоры:

monkeyKind.a
monkeyKind.b

а универсальные морфизмы – как конструкторы:

let u = x => { a : isBeautiful(x), b : isSmart(x) }

В теории категорий акцессоры часто называют деструкторами, потому что они позволяют разобрать сложный объект на составные части, они дуальны конструкторам. При вызове такого деструктора объект совершенно не обязательно должен уничтожаться.

Сумма

Сумма объектов X_j – это объект X и морфизмы i_j : X_j → X, называемые каноническими вложениями, такие что для любого объекта Y и морфизмов f_j : X_j → Y существует единственный морфизм u : X → Y, такой что u ∘ i_j = f_j.

Пример коммутативной диаграммы для двух объектов:

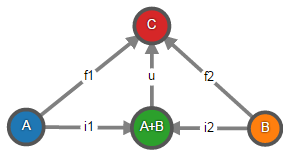
В категории множеств сумма объектов – это дизъюнктивное объединение множеств. Т.е. если в объединяемых множествах есть совпадающие объекты, то эти объекты не будут сливаться, а, грубо говоря, будут некоторым образом отмечены, чтобы можно было понять из какого множества каждый объект.

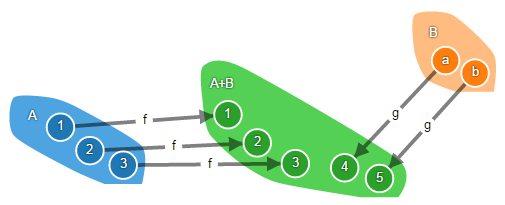
В теории множеств элементы дизъюнктивного объединения обычно помечают некоторым тегами или индексами, например, 1_A, 2_A, 3_A, a_B, b_B. Но в нашем примере элементы суммы – это просто числа от 1 до 5, которые связаны с элементами исходного множества морфизмами f и g. И именно эти морфизмы «помечают» элементы суммы. Как и для произведения само множество без морфизмов не играет особой роли.

Очевидно, что произведение и сумма – это дуальные понятия. Они сформулированы аналогично с точностью до обращения морфизмов.

Но на этом обобщения не заканчиваются. Произведение и сумма очень похожи на конечный и начальный объекты соответственно. Для произведений и конечных объектов можно от каждого объекта категории, удовлетворяющего определённым условиям, построить универсальный морфизм – такие конструкции называют пределами. Для суммы и начального объекта можно к каждому объекту категории, удовлетворяющему определённым условиям, построить универсальный морфизм – такие конструкции называют копределами. Далее вы увидите ещё несколько примеров пределов и копределов.

В общем случае (ко)пределы – это (ко)конусы, определенные для некоторой диаграммы. Как я уже говорил, диаграмма – это функтор из некоторой индексной категории в текущую категорию. Если грубо, то индексная категория определяет «форму», «вид» диаграммы и в итоге определяет какой (ко)предел мы получим (конечный объект, произведение, …). Если дальше развивать эту мысль, то мы рискуем вызвать какодемона.

Короче, идея в том, что даже такие общие понятия, которые мы рассмотрели выше, можно обобщить ещё сильнее.

Чтобы запомнить, чем пределы отличаются от копределов, обратите внимание на то, что универсальные морфизмы всегда направлены (стремятся) к некоторому «предельному» объекту. Равно как и пределы последовательностей или функций стремятся к некоторому значению.

SetCategory.prototype.coproduct = function (A, B) {
  return new SetCoproduct(this).calculate(A, B);
};
function SetCoproduct(cat) {
  this.cat = function () { return cat; };
}
SetCoproduct.prototype.calculate = function (A, B) {
  this.obj = new Set();
  var elementCount = 1;
  function createInjection(set, obj) {
    var mapping = {};
    set.forEach(function (x) {
      obj.add(elementCount);
      mapping[x] = elementCount;
      elementCount++;
    });
    return mapping;
  }
  this.f = this.cat().morphism(A, this.obj, createInjection(A, this.obj));
  this.g = this.cat().morphism(B, this.obj, createInjection(B, this.obj));
  return this;
};
SetCoproduct.prototype.univ = function(m, n) {
  assertEqualCodom(m, n);
  assertEqualDom(this.f, m);
  assertEqualDom(this.g, n);
  var obj = m.codom();
  var mapping = {};
  function addMappings(f, h) {
    h.dom().forEach(function (x) {
      mapping[f.image(x)] = h.image(x);
    });
  }
  addMappings(this.f, m);
  addMappings(this.g, n);
  var u = this.cat().morphism(this.obj, obj, mapping);
  assertCommutes(u.compose(this.f), m);
  assertCommutes(u.compose(this.g), n);
  return u;
};

Попробуем разобраться, что делает универсальный морфизм суммы объектов.

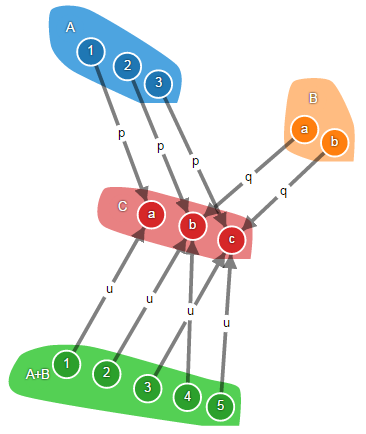
Напомню, что канонические проекции произведения можно рассматривать как деструкторы произведения объктов, а универсальный морфизм – как конструктор. Сумма – это дуальное понятие.

Соответственно, канонические вложения можно рассматривать как конструкторы суммы объектов, а универсальный морфизм – как деструктор. Почитайте про типы-суммы. В том или ином виде они реализованы в очень разных языках программирования. Как правило, в качестве примеров приводят алгебраические типы данных и сопоставление с образцом. Но в JavaScript этого нет, поэтому приведу немного другой пример.

Пусть у нас есть два вида обезьянок – шимпанзе и гориллы – с соответствующими конструкторами:

function Chimpanzee() { }
function Gorilla() { }

Пусть для шимпанзе нам нужно вычислять некоторую функцию p, а для горилл – q, при этом область значений обоих функций – это некоторое множество C. Например, C – это перечисление: маленькая, средняя, большая. Функция p вычисляет категорию, к которой относится шимпанзе в зависимости от размера, а функция q вычисляет категорию для гориллы:

let u = x => switch (typeof x) {
  case 'Chimpanzee': return p(x);
  case 'Gorilla': return q(x);
}

Вычитание (дополнение к сумме)

Если вы что-то читали по теории категорий, то вряд ли увидели выше для себя что-то новое. А слышали ли вы, например, о вычитании объектов в теории категорий? Идея совершенно очевидная, правда, в англоязычных статьях обычно говорят о вычислении coproduct complement. На русский язык можно перевести как вычисление дополнения к сумме объектов. Но, по сути, это операция вычитания.

Пусть имеется сумма объектов A+B, один из слагаемых объектов A и соответствующее ему каноническое вложение i₁. Или просто каноническое вложение i₁, доменом которого является A, а кодоменом – A+B. Если мы вычислим другой канонический морфизм i₂, то фактически вычтем из суммы одно из слагаемых:

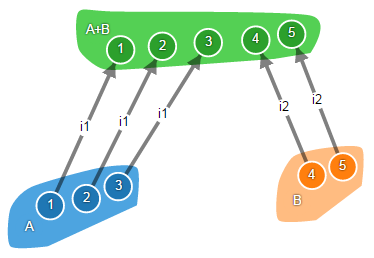
SetCategory.prototype.coproductComplement = function (f) {
  return new SetCoproduct(this).complement(f);
};
SetCoproduct.prototype.complement = function (f) {
  this.obj = f.codom();
  this.f = f;
  this.g = this.cat().morphism(f.codom().diff(f.image()), this.obj).initId();
  return this;
};

В общем случае сумма объектов может быть N-арной, а не только бинарной. Однозначно вычислить дополнение можно только для бинарной суммы. Дополнения к суммам нам потребуются позже для вычисления дополнений к кодекартовым квадратам.

Уравнитель

Выше мы уже рассмотрели (ко)пределы для пустых диаграмм (конечные и начальные объекты) и для дискретных объектов (произведение и сумма). Теперь рассмотрим (ко)пределы для пары параллельных морфизмов, т.е. морфизмов с общими доменом и кодоменом.

Уравнитель параллельных морфизмов f, g : X → Y – это объект E и морфизм eq : E → X, такие что f ∘ eq = g ∘ eq и для любого объекта O и морфизма m : O → X если f ∘ m = g ∘ m, то существует уникальный морфизм u : O → E, такой что eq ∘ u = m, т.е. следующая диаграмма коммутативна.

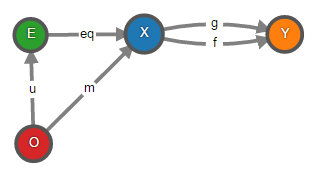
Охх… В своё время я прочитал несколько учебников по теории категорий. И где-то на этом месте переставал понимать о чём вообще идёт речь. Это происходило по двум причинам. Во-первых, я ленился рисовать множества и функции на бумаге и при этом, не будучи Георгием Перельманом, не мог сконструировать всё это в воображении. Как следствие, я не понимал эти конструкции даже для категории множеств, не говоря о других категориях. Далее будут диаграммы, на которых визуально виден смысл уравнителя. Во-вторых, даже более простые произведение и сумму объектов я понимал только на интуитивном уровне, не понимая смысл универсального свойства. В общем-то и в этой статье я пока не рассматривал толком универсальное свойство. Разберёмся с ним более детально на примере уравнителя.

Сначала разберёмся с условием f ∘ eq = g ∘ eq. Для удобства изобразим объект X и морфизм eq дважды, чтобы морфизмы f и g не накладывались друг на друга.

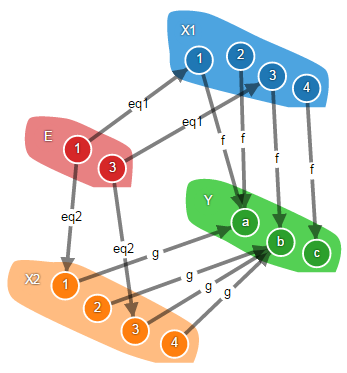
Морфизмы f и g отображают элемент «1» множества X на элемент «a» множества Y. Следовательно, если морфизм eq будет отображать некий элемент «1» множества E на элемент «1» множества X, то будет выполнено равенство f(eq(1)) = g(eq(1)) = a. На рисунке видно, что пути, начинающиеся с элемента «1» в множестве E, заканчиваются одними и тем же элементом в множестве Y.

Морфизм f отображает элемент «2» на элемент «a», а морфизм g отображает элемент «2» на элемент «b». Следовательно, как не реализуй отображение eq, при прохождении через элемент «2» в множестве X пути разойдутся. Т.е. какой элемент не подставь вместо вопросительного знака f(eq(?)) = a никогда не будет равно g(eq(?)) = b, потому что элемент «a» не равен «b».

Продолжаем эти рассуждения для оставшихся элементов множеств X и Y и таким образом завершаем формирование E и eq. Только элементы «1» и «3» отображаются функциями f и g одинаково.

Это должно быть относительно понятно, при вычислении E и eq мы действительно находим что-то общее между f и g. Но зачем в определении объект O и морфизмы m и u? Дело в том, что множество E и морфизм eq, которые мы сконструировали, не уникальные. Добавим на диаграмму O и m, для которых тоже выполняется f ∘ m = g ∘ m.

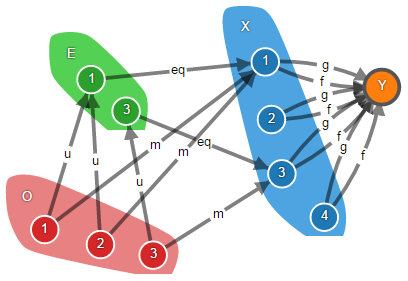
Получается, что m уравнивает f и g не хуже, чем eq. Чем вообще eq лучше m? Таких уравнителей мы можем построить бесконечное количество. Очевидно, что E и eq проще, чем O и m и поэтому, наверное, лучше. Но в теории категорий мы не можем сказать, что морфизм уравнителя должен содержать наименьшее количество элементов, потому что, как я уже отмечал, мы максимально абстрагируемся от внутреннего устройства объектов и морфизмов. В какой-нибудь другой категории нет никаких множеств и функций, поэтому привязываясь к количеству элементов, мы очень сильно ограничили бы применимость уравнителей.

Итак, как из всех потенциальных уравнителей выбрать лучший? На помощь приходит универсальное свойство. От объекта E к объекту O можно провести два морфизма h, для которых выполняется условие m ∘ h = eq, это {(1,1),(3,3)} и {(1,2),(3,3)}. А, следовательно, O и m не являются уравнителем, так как для них не выполняется универсальное свойство.

А, вот, для E и eq универсальное свойство как-раз выполняется. Мы можем вычислить универсальный морфизм для O и m и получим u = {(1,1),(2,1),(3,3)}. Для других O и m, для которых выполняется f ∘ m = g ∘ m, универсальный морфизм будет другой, но всё равно уникальный.

А что если O и m будут соответственно такого же размера как E и eq? Какой уравнитель будет лучше? Они изоморфны, с точки зрения теории категорий не существенно какой выбрать.

И только скажите, что теория категорий не нужна простому работяге, фигачящему на JavaScript! Нужна, она позволяет узреть истинное абстрагирование, а не то, что называют абстрагированием всякие ООПшники и иже с ними (ирония).

SetCategory.prototype.equalizer = function (f, g) {
  return new SetEqualizer(this).calculate(f, g);
};
function SetEqualizer(cat) {
  this.cat = function () { return cat; };
}
SetEqualizer.prototype.calculate = function (f, g) {
  assertParallel(f, g);

  this.f = function () { return f };
  this.g = function () { return g };

  var dom = new Set();
  var codom = f.dom();
  this.q = this.cat().morphism(dom, codom);
  f.dom().forEach(function (x) {
    if (f.image(x) == g.image(x)) {
      dom.add(x);
      this.q.push(x, x);
    }
  }.bind(this));

  this.obj = this.q.dom();

  assertCommutes(f.compose(this.q), g.compose(this.q));
  return this;
}
SetEqualizer.prototype.univ = function (m) {
  assertEqualCodom(this.q, m);
  assertCommutes(this.f().compose(m), this.g().compose(m));
  var mapping = {};
  m.forEach(function (x, y) {
    mapping[x] = this.q.preimage(y).representative();
  }.bind(this));
  var u = this.cat().morphism(m.dom(), this.obj, mapping);
  assertCommutes(this.q.compose(u), m);
  return u;
};

Отметим ещё один момент. В учебниках по теории категорий написано, что любой уравнитель – это мономорфизм. Внимательный читатель наверняка заметил, что условие f ∘ eq = g ∘ eq для уравнителя очень похоже на условие f ∘ m = g ∘ m для… эпиморфизма. Стоп, почему эпиморфизма, а не мономорфизма? В данном случае схожесть уравнений приводит к возникновению ложных аналогий.

Равенство для эпиморфизма можно сократить на эпиморфизм и при этом будет выполняться равенство f = g. А, вот, если сократить равенство на уравнитель, то морфизм f не будет равен g. Скорее наоборот, уравнитель, как правило, применяется к неравным морфизмам. В этом легко убедиться, если ещё раз посмотреть на рисунки выше. Морфизмы f и g не равны, а уравнитель eq не является сюръекцией (эпиморфизмом в категории множеств).

Ок, но почему он тогда является мономорфизмом? Это следует из универсального свойства. Любые два морфизма от некоторого объекта O к объекту E будут равны. С другой стороны, видно, что в нашем примере уравнитель – это инъекция (мономорфизм в категории множеств), и универсальное свойство гарантирует, что это всегда будет инъекция.

Зачем я описываю всю эту жесть? Чтобы ещё раз показать, что для «простых» категорий можно понять смысл разных конструкций или теорем, представляя какие реальные вещи (множества, функции) за всем этим стоят. Вы никогда не поймёте, что всё это значит, если не будете рисовать подобные картинки.

Коуравнитель

Коуравнитель параллельных морфизмов f, g : X → Y – это объект Q и морфизм q : Y → Q, такие что q ∘ f = q ∘ g и для любого объекта O и морфизма m : Y → O если m ∘ f = m ∘ g, то существует уникальный морфизм u : Q → O, такой что u ∘ q = m, т.е. следующая диаграмма коммутативна.

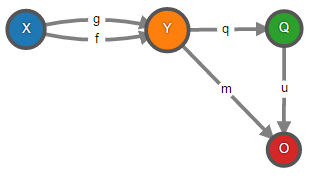
Как видите, определение аналогично определению уравнителя, только морфизмы направлены в обратную сторону. Однако, вычислительная составляющая коуравнителя, на первый взгляд, не имеет ничего общего с тем, что мы рассматривали в предыдущем разделе.

Рассмотрим это на примере конкретных множеств и функций.

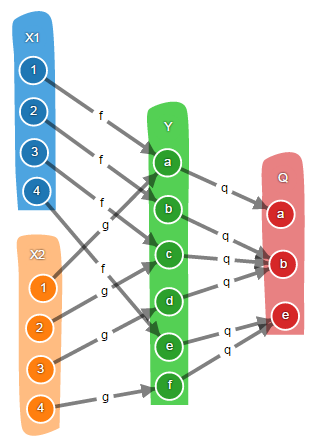
Оба морфизма f и g, для которых мы вычисляем коуравнитель, отображают элемент «1» множества X на элемент «a» множества Y. Чтобы выполнялось равенство q(f(1)) = q(g(1)), достаточно, чтобы морфизм q просто отображал элемент «a» на некий элемент «a» множества Q.

Морфизм f отображает элемент «2» на элемент «b», а морфизм g отображает элемент «2» на элемент «c». Чтобы выполнялось равенство q(f(2)) = q(g(2)), морфизм q должен отображать элементы «b» и «c» на некий элемент «b» множества Q. Иными словами, мы объединили элементы «b» и «c» в один класс эквивалентности «b».

Морфизм f отображает элемент «3» на элемент «c», а морфизм g отображает элемент «3» на элемент «d». Как и ранее, это означает, что «c» и «d» необходимо объединить в один класс эквивалентности. Однако «c» уже принадлежит классу «b», поэтому мы не создаём новый класс, а просто относим элемент «d» к классу «b».

Аналогично создаём класс эквивалентности «e» для элементов «e» и «f». И завершаем формирование коуравнителя Q с морфизмом q.

Однако, руководствуясь такой логикой, мы можем построить некоторый объект O с морфизмом m, для которых так же как и для коуравнителя выполняется условие m ∘ f = m ∘ g. Причём, O и m будут даже проще, чем Q и q.

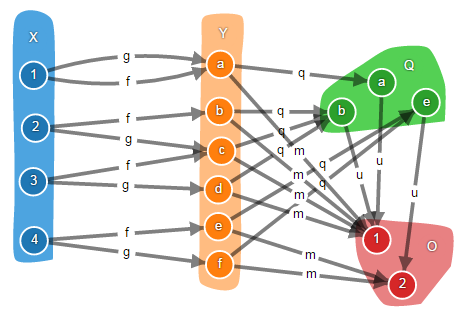
Но O и m не будут являться коуравнителем, потому что для них не выполняется универсальное свойство, и поэтому они в некотором смысле хуже, чем Q и q. Хуже тем, что они слишком простые, они не различают классы «a» и «b», смешивая их в класс «1».

Обратите внимание на то, что универсальное свойство уравнителя позволяет отобрать наименьшие объект и морфизм среди всех потенциально подходящих. А универсальное свойство коуравнителя – позволяет отобрать наибольшие объект и морфизм. Наверное, многие подобные задачи структурной оптимизации можно свести к поиску (ко)пределов в той или иной категории.

SetCategory.prototype.coequalizer = function (f, g) {
  return new SetCoequalizer(this).calculate(f, g);
};
function SetCoequalizer(cat) {
  this.cat = function () { return cat; };
}
SetCoequalizer.prototype.calculate = function (f, g) {
  assertParallel(f, g);

  this.f = function () { return f };
  this.g = function () { return g };

  var dom = f.codom();
  var codom = new Set();
  var eq = {};
  f.dom().forEach(function (x) {
    var fx = f.image(x);
    var gx = g.image(x);
    eq[fx] = eq[gx] = has(eq, fx) ? eq[fx] : has(eq, gx) ? eq[gx] : fx;
  });
  this.q = this.cat().morphism(dom, codom);
  dom.forEach(function (s) {
    var t = eq[s] || s;
    codom.add(t);
    this.q.push(s, t);
  }.bind(this));

  this.obj = this.q.codom();

  assertCommutes(this.q.compose(f), this.q.compose(g));
  return this;
}
SetCoequalizer.prototype.univ = function (m) {
  assertEqualDom(this.q, m);
  assertCommutes(m.compose(this.f()), m.compose(this.g()));
  var mapping = {};
  m.dom().forEach(function (x) {
    mapping[this.q.image(x)] = m.image(x);
  }.bind(this));
  var u = this.cat().morphism(this.q.codom(), m.codom(), mapping);
  assertCommutes(u.compose(this.q), m);
  return u;
};

Коуравнитель – это очень полезная с точки зрения ИТ конструкция. Он позволяет решать различные задачи унификации: унификации типов в языках программирования, унификации выражений в системах компьютерной алгебры, унификации графов. Из той же области задачи слияния моделей или исходного кода. Мы вернёмся к этому в следующих статьях.

Декартов квадрат (расслоённое произведение)

Уравнитель вычисляется для двух параллельных морфизмов. А что, если вычислить предел для двух морфизмов, у которых совпадает только кодомен? Мы получим ещё один вид предела – декартов квадрат.

Декартов квадрат морфизмов f : X → Z и g : Y → Z – это объект P и морфизмы p : P → X и q : P → Y, такие что f ∘ p = g ∘ q и для любого объекта Q и морфизмов m : Q → X и n : Q → Y, если f ∘ m = g ∘ n, то существует уникальный морфизм u : Q → P, такой что p ∘ u = m и q ∘ u = n, т.е. следующая диаграмма коммутативна.

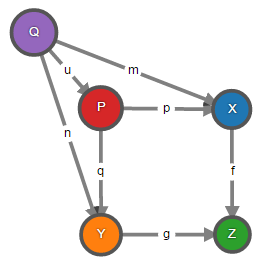
Выглядит сложно, но в категории множеств это всего-навсего расслоённое произведение:

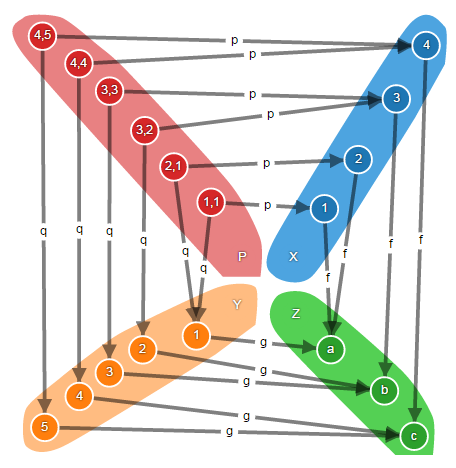
На рисунке видно, что множество P содержит пары элементов из множеств X и Y, но не все возможные, как в случае с декартовым произведением, а только такие, составные элементы которых функциями f и g отображаются на одни и те же элементы множества Z.

Если вы попробуете в исходном коде найти реализацию декартова квадрата для категории множеств, то не сможете, потому что он реализован для любой полной категории, а не только категории множеств.

CompleteCategory.prototype.pullback = function (f, g) {
  return new Pullback(this).calculate(f, g);
};
function Pullback(cat) {
  this.cat = function () { return cat; };
}
Pullback.prototype.calculate = function (f, g) {
  assertEqualCodom(f, g);
  this.f = f;
  this.g = g;

  var prod = this.cat().product(f.dom(), g.dom());
  this.product = function () { return prod; };

  var eq = this.cat().equalizer(f.compose(prod.f), g.compose(prod.g));
  this.equalizer = function () { return eq; };

  this.p = prod.f.compose(eq.q);
  this.q = prod.g.compose(eq.q);
  this.obj = eq.obj;
  assertCommutes(this.f.compose(this.p), this.g.compose(this.q));
  return this;
}
Pullback.prototype.univ = function (m, n) {
  assertEqualDom(m, n);
  assertEqualCodom(m, this.p);
  assertEqualCodom(n, this.q);
  var u = this.equalizer().univ(this.product().univ(m, n));
  assertCommutes(this.p.compose(u), m);
  assertCommutes(this.q.compose(u), n);
  return u;
};

Декартов квадрат вычисляется следующим образом. Сначала получаем произведение объектов X и Y, а затем вычисляем уравнитель для двух параллельных морфизмов f ∘ π₁ и g ∘ π₂. Объект уравнителя – это и есть объект P декартова квадрата. Морфизм p вычисляется как π₁ ∘ eq, а q – как π₂ ∘ eq. Универсальное свойство декартова квадрата вычисляется на основе универсальных свойств произведения и уравнителя.

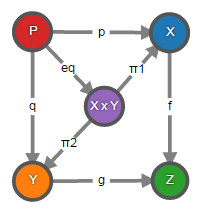
Причём, этот алгоритм применим в любой полной категории: категории топологических пространств, групп, колец и т.п. Я понятия не имею, что это за категория топологических пространств, но я знаю, что она полная и значит в ней будет работать этот алгоритм. Это пример профита, получаемого благодаря абстрагированию от внутреннего представления объектов и морфизмов. Более того, в полной категории можно вычислять и более сложные пределы с произвольной диаграммой на основе простейших пределов, рассмотренных в данной статье.

Кодекартов квадрат (универсальный квадрат)

Кодекартов квадрат морфизмов f : Z → X и g : Z → Y – это объект P и морфизмы p : X → P и q : Y → P, такие что p ∘ f = q ∘ g и для любого объекта Q и морфизмов m : X → Q и n : Y → Q, если m ∘ f = n ∘ g, то существует уникальный морфизм u : P → Q, такой что u ∘ p = m и u ∘ q = n, т.е. следующая диаграмма коммутативна.

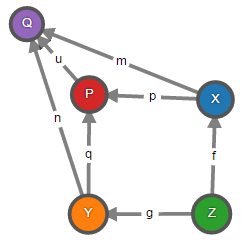
Кодекартов квадрат дуален декартову квадрату и может быть вычислен в любой кополной категории как коуравнитель морфизмов i₁ ∘ f и i₂ ∘ g, где i₁ и i₂ – это канонические включения суммы объектов X и Y. Морфизмы p и q вычисляются как h ∘ i₁ и h ∘ i₂ соответственно, где h – морфизм коуравнителя:

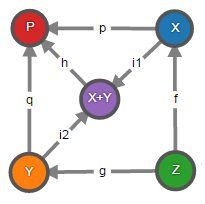
Иными словами, множество P – это дизъюнктивное объединение множеств X и Y, причём те элементы, у которых одинаковые прообразы в множестве Z, объединены:

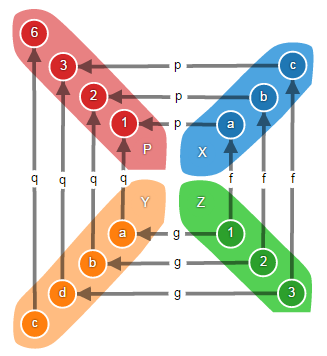
Кодекартов квадрат аналогично коуравнителю используется в задачах унификации. На диаграмме вы видите, что элементы «a» и «b» из множеств X и Y были унифицированы в множестве P в элементы «1» и «2» соответственно. Элемент «c» из множества X был унифицирован с элементом «d» из множества Y. А элемент «c» из множества Y не был ни с чем унифицирован.

С помощью кодекартова квадрата можно решать и более интересные задачи. Пусть известны морфизмы g и q. Если мы вычислим морфизмы f и p, то фактически получим объект X удалением из P всего, что присуще только Y. Это называется вычислением дополнения к кодекартову квадрату. В следующих статьях на примере графов это будет более наглядно.

Ещё раз обращаю ваше внимание на то, что вычисление кодекартова квадрата (как, кстати, и дополнения к нему) реализовано независимо от множеств, функций и прочих деталей внутреннего устройства той или иной категории:

CocompleteCategory.prototype.pushout = function (f, g) {
  return new Pushout(this).calculate(f, g);
};
function Pushout(cat, f, g) {
  this.cat = function () { return cat; };
}
Pushout.prototype.calculate = function (f, g) {
  assertEqualDom(f, g);
  this.f = f;
  this.g = g;

  var cp = this.cat().coproduct(f.codom(), g.codom());
  this.coproduct = function () { return cp; };

  var ceq = this.cat().coequalizer(cp.f.compose(f), cp.g.compose(g));
  this.coequalizer = function () { return ceq; };

  this.p = ceq.q.compose(cp.f);
  this.q = ceq.q.compose(cp.g);
  this.obj = ceq.obj;
  assertCommutes(this.p.compose(this.f), this.q.compose(this.g));
  return this;
}
Pushout.prototype.univ = function (m, n) {
  assertEqualCodom(m, n);
  assertEqualDom(m, this.p);
  assertEqualDom(n, this.q);
  var u = this.coequalizer().univ(this.coproduct().univ(m, n));
  assertCommutes(u.compose(this.p), m);
  assertCommutes(u.compose(this.q), n);
  return u;
};

Что почитать

Фактически, моя статья является плагиатом идей из этой книги, единственное, вместо JavaScript они используют ML:
D.E. Rydeheard, R.M. Burstall. Computational Category Theory, 1988

Также я сплагиатил много идей отсюда, но об этом уже в следующих частях:
Hans Jürgen Schneider. Graph Transformations. An Introduction to the Categorical Approach, 2011

Сам не читал, только листал, но, вроде, неплохая книга с множеством примеров, написанная простым языком:
Peter Smith, Category Theory. A Gentle Introduction, 2016

Должно быть интересно тем, кто пишет на функциональных языках программирования:
Maarten M. Fokkinga. A Gentle Introduction to Category Theory — the calculational approach, 1994

Ещё пара не очень простых книг для тех, кто пишет на функциональных ЯП:
Andrea Asperti, Giuseppe Longo. Categories, Types and Structures. Category Theory for the working computer scientist, 1991
Michael Barr, Charles Wells. Category Theory for Computing Science, 1998

Конечно, стоит почитать цикл статей «Теория категорий для программистов» (оригинал — Bartosz Milewski), но, на мой взгляд, он ориентирован преимущественно на людей, пишущих на ФЯП. У нас немного другой подход, вернёмся к этому в заключении.

В данной статье мы максимально абстрагировались от элементов множеств. Но, вообще, в теории категорий есть понятие элемент объекта. Оно более общее, но по смыслу похоже на элемент множества. Также в теории категорий есть обобщение идеи подмножеств — подобъекты. Я надеюсь, мы вернёмся к ним в следующих статьях, а пока можно посмотреть следующую книгу. Хотя она и рассчитана на математиков, но, по крайней мере, в 1-ой главе язык относительно простой:
Michael Barr, Charles Wells. Toposes, Triples and Theories, 1985

Тем, кто интересуется базами данных, рекомендую почитать статьи чела по имени David I. Spivak. Я сам только листал, но выглядит очень интересно.

Интересная статья про приложение теории категорий к нейронным сетям:
Michael J. Healy. Category Theory Applied to Neural Modeling and Graphical Representations, 2000

Заключение

В статье вы увидели вычислительный аспект теории категорий. Обычно, когда говорят о вычислениях, то вспоминают декартово замкнутые категории или монады Но в теории категорий за большинством конструкций стоят те или иные вычисления, а не только за монадами. Теория категорий в большей степени о вычислениях на структурах, чем о самих структурах.

Я встречал два способа объяснить ИТшнику, что такое теория категорий. Некоторые авторы рассматривают в качестве категории систему типов и функции некоторого языка программирования. Например, в Haskell такая категория называется Hask. В данной статье используется другой подход. Мы рассмотрели категорию множеств как есть, не увязывая множества с типами данных, а морфизмы с функциями некоторого ЯП. Для каждой рассмотренной конструкции мы увидели её вычислительный аспект и реализовали его. Таким образом можно реализовать любую категорию на любом языке программирования. Совершенно не обязательно пытаться каким-то образом встроить теорию категорий в этот язык.

В статье вы увидели примеры абстрагирования от деталей внутреннего устройства объектов и морфизмов. Например, увидели, как можно определить сюръективные функции или декартово произведение, ничего не говоря о множествах. Абстрагирование в программировании очень похоже на абстрагирование в теории категорий. У меня даже ощущение, что тот, кто придумал ООП, черпал вдохновение из теории категорий.

После прочтения статьи вы должны понимать, что универсальное свойство – это, по сути, абстрактное представление некоторой задачи на поиск оптимальной структуры.

Также вы увидели профит от применения теории категорий.

Во-первых, она помогает правильно организовывать код, правильно называть классы и функции. Например, я мог бы назвать метод вычисления декартова произведения множеств calcCartesianProduct(), мог бы придумывать какие-нибудь функции типа multiplyFunctions(). Но благодаря теории категорий я понимаю, что произведения объектов бывают и в других категориях и не сводятся только к декартову произведению, а произведение функций — это универсальный морфизм произведения. Т.е. у совершенно разных категорий будет единый интерфейс.

Во-вторых, теория категорий позволяет писать универсальные алгоритмы, типа вычисления декартова квадрата, которые могут повторно использовать для разных категорий.

В-третьих, теория категорий позволяет писать код, очень хорошо покрытый проверками. Обратите внимание, что во многих функциях проверяются различные предусловия и постусловия (вызовы assert в начале и конце функций соответственно). Причём, мне не нужно как-то искусственно придумывать эти проверки, они следуют из определений!

И, вообще, обратите внимание на тот как написан весь код в статье. Сначала мы описываем некоторое внешнее поведение объекта, его соотношение с другими объектами, в декларативном виде описываем различные универсальные свойства, инварианты, которые должны выполняться для данного объекта. А затем думаем, как это декларативное описание реализовать в коде. При этом реализация получается «правильная», универсальная и покрытая проверками.

Возможно, вы узнали что-то интересное о примесях и смесях в JavaScript.

В предыдущей статье я немного говорил о применении теории категорий для преобразования моделей. В следующих статьях мы будем двигаться в этом направлении и рассмотрим категорию графов, категорию графов с метками и более подробно остановимся на кодекартовых квадратах.

Исходные коды и примеры из статьи.

Автор:

Источник