Чтобы освоить азы Web программирования, я решил написать HTML5 игру — головоломку под названием Triplex (www.quadpuzzle.ru). Написать игру для себя и для друзей — полдела. Захотелось довести проект до ума, сделав из игры продукт для широкого круга пользователей. Насколько получилось — судить вам.
Чтобы освоить азы Web программирования, я решил написать HTML5 игру — головоломку под названием Triplex (www.quadpuzzle.ru). Написать игру для себя и для друзей — полдела. Захотелось довести проект до ума, сделав из игры продукт для широкого круга пользователей. Насколько получилось — судить вам.
Правила игры просты. На игровом поле разложены фигуры из квадратиков. Цель игры — уложить все фигуры в указанный прямоугольник. Вращать можно только одну фигуру, помеченную кружком, если она есть. Решение в каждой задаче существует и единственное.


Работает в свежих версиях следующих браузеров: Opera, Opera-mobile, Safari (Windows, iPad2), Android (HTC Desire, Samsung Galaxy Tab 10.1), Chrome, FireFox и IE9.
Реализованы следующие идеи:
- Игра состоит из одного html файла. Его можно скачать себе на локальный диск и играть без интернета. IE9 этот режим не поддерживает.
- Если есть сетевое подключение, то можно отмечать своё прохождение уровней на сервере и смотреть результаты всех отметившихся игроков.
- В таблице рекордов для каждого уровня хранится имя игрока, решившего этот уровень первым. Также хранится статистика о времени прохождения уровней другими игроками.
- Каждый следующий уровень закодирован решением предыдущего. Поэтому просто взять и пройти последний уровень не получится, не смотря на то, что все уровни хранятся в одном html файле.
- Игра переведена на 5 языков: русский, английский, французский, немецкий и китайский.
Похожие игры
Было бы нечестно умолчать, что игру придумал не я. Прототипом Триплекса стала очень похожая игра BlockPuzzle 500 (www.mtoy.biz), в которую мне довелось играть на своём первом Android телефоне.

По существу Триплекс отличается от неё следующим:
- размером фигур:
BlockPuzzle использует фигуры из 2-х, 3-х, 4-х и 5-и квадратиков, в Триплексе фигуры только из 2-х и 3-х; - в Triplex на одном уровне может быть несколько одинаковых фигур, а в BlockPuzzle все разные;
- в BlockPuzzle нет вращаемых фигур, в Триплексе на некоторых уровнях есть одна вращаемая фигура;
- BlockPuzzle есть только для Андроида, а в Триплекс можно играть на любом устройстве, если на нём установлен браузер с поддержкой HTML5.
Честно признаться, на Андроиде приятнее играть в BlockPuzzle — интерфейс отзывчивее. Буду рад, если кто-то захочет портировать Триплекс на Андроид или другую платформу. Всё что нужно есть в triplex.html.
Откуда взялись задачи
Генератор уровней для этой игры разрабатывался первым. Вначале просто ради любопытства. Хотелось понять природу и свойства таких задач. Сколько их всего, как сложно найти такие задачи, насколько сложно их решать,… Была написана программа на языке Java, которая умеет генерировать уровни. Захотелось с этими уровнями поиграть, потрогать, порешать. Я, видимо, в детстве не наигрался с кубиками, поэтому теперь захотелось поиграть с квадратиками. Возникла идея не только сделать программу визуализации уровней с элементами пользовательского интерфейса, но и сделать из этого всего игру.
Генератор искал уровни следующим образом:
- перебрал все комбинации на полях 3x2, 3x3, 4x3,… с 3-мя и более фигурами из 2-х и 3-х квадратиков;
- исключил все похожие (с точностью до поворотов и отражений);
- из них выбрал такие, в которых есть только одно решение;
- выбрал одну вращаемую фигуру, если это не добавляло других решений.
Вычислительная сложность алгоритма
Изначально программа задумывалась для подбора задач с произвольным количеством и размером фигур произвольных размеров. Алгоритм работает по методу ветвей и границ.
Пусть фигура-решение это прямоугольная фигура размера WxH, состоящая из других фигур (фигур из условия задачи). Рассмотрим все пары соприкасающихся квадратиков (квадратиков с общей гранью), из которых состоит решение. Всего таких граней (2 * W * H — W — H).
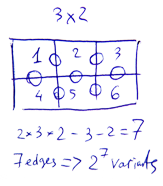
Каждая грань может находится в одном из двух состояний:
0. закрыта — соседние квадратики могут принадлежать разным фигурам;
1. открыта — два соседних квадратика принадлежат одной фигуре.
Назовём N-ку из (2 * W * H — W — H) бинарных значений набором состояний всех граней. Очевидно, что произвольному набору состояний однозначно соответствует некоторое разбиение прямоугольника на фигуры (смотрите описание алгоритма раскраски разбиения). Очевидно, что для любого разбиения найдётся хотя бы один набор состояний.
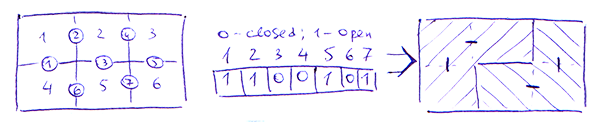
Множество всевозможных наборов состояний содержит 2(2 * W * H — W — H) элементов. То есть, чтобы перебрать все возможные разбиения, достаточно запустить цикл от 0 до 2(2 * W * H — W — H)-1, и рассматривать каждый i-ый бит бинарного представления индексной переменной состоянием i-ой грани. Если сложность тела цикла ограничить константой, то общая сложность перебора всех комбинаций будет экспоненциальной от площади решения. Давайте прикинем, сколько итераций получится.
| размерность | количество итераций |
|---|---|
| 1x1 | 2(2 * 1 * 1 — 1 — 1) = 20=1 |
| 2x1 | 2(2 * 2 * 1 — 2 — 1) = 21=2 |
| 2x2 | 2(2 * 2 * 2 — 2 — 2) = 24=16 |
| 2x3 | 2(2 * 2 * 3 — 2 — 3) = 27=128 |
| 2x4 | 2(2 * 2 * 4 — 2 — 4) = 210=1024 |
| 3x3 | 2(2 * 3 * 3 — 3 — 3) = 212=4096 |
| ... | ... |
| 6x6 | 2(2 * 6 * 6 — 6 — 6) = 260 |
То есть индекс цикла для задачи 6x6 ещё помещается в 64-битный целочисленный тип. Если запустить такой цикл с пустым телом со скоростью 1 процессорный такт на итерацию на процессоре с частотой 3GHz, то программа будет работать 12 лет = 260 / (3*109 * 3600 * 24 * 365).
Сокращение перебора, фильтрация
Для того, чтобы существенно сократить перебор, нужно стараться откидывать целые группы таких разбиений, которые заведомо не подходят. Для этого был придуман следующий механизм фильтрации. Упорядочим все квадратики по убыванию слева на право и сверху вниз: левый верхний — самый старший, правый нижний — самый младший. Каждому квадратику однозначно соответствует его пара граней: правая и нижняя. Так что, порядок на квадратиках, естественным образом, индуцирует порядок на соприкасающихся гранях: пусть будет нижняя — старшая, правая — младшая. Каждое разбиение проходит от одного фильтра к следующему через функцию-фильтр, которая либо пропускает разбиение дальше, либо нет. Если разбиение проходит все фильтры, то оно попадает в нашу игру. Если разбиение не удовлетворяет условию какого-нибудь фильтра, то фильтр может указывать самый младший квадратик, из-за которого условие не выполняется. Тогда перебор разбиений продолжается не с самой младшей грани, а с младшей грани указанного квадратика.
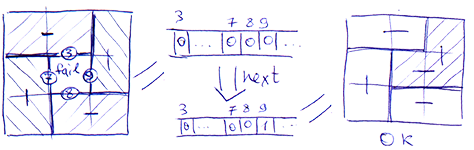
В общем случае для произвольного фильтра трудно оценить, на сколько таким образом удаётся сократить количество разбиений. Однако, очень простой пример показывает, что иногда значительно. Так, благодаря фильтру, который отбрасывает разбиения с изолированными квадратиками (квадратиками, которые являются самостоятельной фигурой из одного квадратика), количество разбиений на первом же шаге сокращается на 25%: самый старший квадратик должен иметь хотя бы одну общую грань с одним из двух соседей. То есть вместо 12 лет, нам оказывается хватит 9. Если 4 угловых квадратика не являются соседями, то фильтр «изолированных квадратиков» сокращает перебор на 25% для каждого из них, а это уже (1 — (3/4)4) = 68%. Аналогичные соображения для остальных квадратиков в сумме дают сокращение перебора порядка O(2W*H).
Для генерации уровней Triplex были использованы следующие фильтры в указанном порядке:
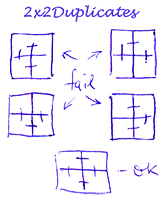
1. 2x2Duplicates
— фильтр, отбрасывающий разбиения, в которых есть четыре квадратика (2x2), принадлежащих одной фигуре, но хотя бы одна из четырёх общих граней не общая.
2. 1x1Cell
— фильтр изолированных квадратиков, описанный выше.
3. StraightCut
— фильтр, отбрасывающий разбиения с прямыми горизонтальными или вертикальными разрезами. Такой разрез делит разбиение на две части, переставив которые, мы получим второе решение. Это правило не выполняется только тогда, когда обе части разбиения состоят из одинаковых наборов. В этом случае второго решения не получается, но для нашей игры разбиение не представляет интерес, потому что каждая часть разбиения является самостоятельной задачей меньшей размерности.
4. Shapes3
— фильтр, отбрасывающий задачи с количеством фигур меньше 3. Задачки из двух фигур решать совсем не интересно.
5. Shape23
— фильтр, отбрасывающий разбиения, в которых есть фигуры из 4 и более квадратиков. Этот фильтр специфичный для Триплекса.
6. RotatedAndReflected
— фильтр, который отбрасывает одинаковые разбиения — такие разбиения, которые получаются друг из друга поворотом на 90, 180 или 270 градусов и/или зеркальным отражением. Каждому разбиению таким образом сопоставляется 8 одинаковых разбиений. Поскольку на множестве разбиений у нас введён линейный порядок, то из каждой восьмёрки можно выбрать минимальное разбиение. Если фильтруемое разбиение не является минимальным, то мы его отбрасываем. Это означает, что мы уже рассматривали разбиение из этой восьмёрки.
7. Solver
— фильтр, отбрасывающий разбиения, для которых существует более одного решения. Этот фильтр, наверное, наиболее интересен, однако не хочется описывать алгоритм его работы, чтобы не облегчать задачу тем, программистам, кто захочет написать свой решатель, чтобы пройти игру. Хочется сказать, однако, что Solver подбирает решения методом ветвей и границ. Количество листьев на 'ветвях' (количество комбинаций) вычисляется по формуле
C!/(C1!C2!...Cm!),
где C — количество фигур в разбиении, m — количество различных фигур в разбиении (количество групп одинаковых фигур), Ci — количество одинаковых фигур в каждой из групп. Для примера, если все фигуры одинаковые, то комбинация всего одна: m = 1 и С = С1. Первый уровень (3 различные фигуры, пока не обращаем внимание на вращаемую фигуру) даёт 3!/(1!1!1!) = 6 комбинаций. Десятый уровень (6 фигур в четырёх группах) даёт 6!/(2!2!1!1!) = 180 комбинаций. Сотый уровень (9 фигур, в пяти группах) даёт 9!/(3!3!1!1!1!) = 10080 комбинаций. Шестисотый уровень даёт около 1011 комбинаций. Не смотря на то, что комбинаций много, Solver прорешивает все задачки Триплекса за 1-2 секунды. Это говорит о том, что найти задачи намного сложнее, чем их решить. Так, например, при поиске задач 6x6 Solver решил 5887655 задач, выбрав из них всего 46.
Для Триплекса, с фигурами из двух и трёх квадратиков, описанный набор фильтров далеко не оптимален. Но программа проектировалась для генерации более сложных задач, а Триплекс это всего лишь частный случай, для которого есть совершенно другой, более простой алгоритм, о котором я расскажу дальше.
Стоит отметить, что порядок фильтров очень сильно влияет на производительность программы. В начало списка надо ставить фильтры, у которых наименьшая алгоритмическая сложность, и те, которые отбрасывают максимальное количество плохих разбиений большими группами. Например, Solver, если его поставить первым, скорее всего, откинет наибольшее количество разбиений. Однако он будет работать неприемлемо долго, оценивая разбиения по одному.
Отчёт генератора
Рассмотрим отчёт о генерации задач для размерности 6x6. В следующий таблице показано сколько разбиений было обработано и какими фильтрами.
| проверено | принято | отброшено | отброшено % | отброшено % от общего числа |
фильтр |
|---|---|---|---|---|---|
| 596745944245 | 295317406559 | 301428537686 | 50.51 | 50.51 | 2x2Duplicates |
| 295317406559 | 110686580321 | 184630826238 | 62.52 | 30.94 | 1x1Cell |
| 110686580321 | 79876633976 | 30809946345 | 27.84 | 5.16 | StraightCut |
| 79876633976 | 79875530828 | 1103148 | 0.00 | 0.00 | Shapes3 |
| 79875530828 | 47094698 | 79828436130 | 99.94 | 13.38 | Shape23 |
| 47094698 | 5887701 | 41206997 | 87.50 | 0.01 | RotatedAndReflected |
| 5887701 | 46 | 5887655 | 100.00 | 0.00 | Solver |
| 596745944245 | 46 | 596745944199 | 100.00 | 100.00 | Total |
Первое, на что хочется обратить внимание, — общее число проверенных разбиений — 596745944245 < 240. То есть, благодаря механизму 'границ' удалось сократить проверку с 260 до 240. Если учесть, что эта задача крутилась 12 дней, то без механизма 'границ' она бы работала 12*220 ~ 12*106 дней или пришлось бы использовать миллион процессорных ядер вместо одного. В этой таблице не хватает одного очень интересного столбца, который бы показал, насколько каждый из фильтров сократил перебор, чтобы понять, из чего состоит делитель 220.
Как и следовало ожидать, RotatedAndReflected откинул 7/8 = 87.5% всех данных ему разбиений, выбрав лишь одну из каждой восьмёрки одинаковых задач. Интересно отметить, что из рассмотренных разбиений, встретилось больше миллиона различных вариантов, отброшенных фильтром Shapes3, — вариантов разбиения из двух фигур. Даже трудно себе представить, что из квинтиллиона (260 ~ 1018) разбиений 6x6 для Триплекса было выбрано всего 46. Как говорится, «всё самое лучшее».
Временной график
Так выглядят для задачи 6x6 графики зависимости количества найденных уровней (LEVELS FOUND) от времени и % рассмотренных разбиений (WORK DONE) от времени (в днях).
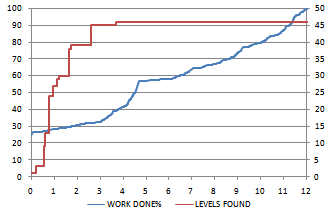
Хочется отметить два момента:
- Во-первых, WORK DONE начинается со значения 25% благодаря фильтру изолированных квадратиков применённому к левому верхнему квадратику, как объясняется выше.
- Во-вторых, не смотря на то, что программа работала 12
дней, все уровни были найдены в первые 4 дня на значениях WORK DONE от 25% до 40%. С другими размерностями тоже самое — большинство найденных уровней были найдены вначале перебора. Это происходит из-за фильтра RotatedAndReflected, в котором из восьмёрки одинаковых задач выбирается минимальная.
Таблица размерностей задач
В этой таблице приведены данные по всем задачам, которые попали в игру.
| Площадь решения |
Размерность | Количество уровней |
Время | Общее количество уровней |
Общее время |
|---|---|---|---|---|---|
| 8 | 4x2 | 2 | 0сек | 2 | 0сек |
| 9 | 3x3 | 1 | 0сек | 3 | 0сек |
| 10 | 5x2 | 1 | 0сек | 4 | 0сек |
| 12 | 4x3 | 4 | 0сек | 8 | 0сек |
| 15 | 5x3 | 6 | 0сек | 14 | 0сек |
| 16 | 4x4 | 5 | 0сек | 19 | 0сек |
| 18 | 6x3 | 8 | 0сек | 27 | 0сек |
| 20 | 5x4 | 48 | 0сек | 75 | 0сек |
| 21 | 7x3 | 16 | 0сек | 91 | 0сек |
| 24 | 6x4 | 27 | 2мин | 118 | 2мин |
| 8x3 | 16 | 1мин | 134 | 3мин | |
| 25 | 5x5 | 22 | 3мин | 156 | 6мин |
| 27 | 9x3 | 19 | 12мин | 175 | 17мин |
| 28 | 7x4 | 45 | 41мин | 220 | 59мин |
| 30 | 6x5 | 55 | 3час | 275 | 4час |
| 10x3 | 19 | 2час | 294 | 6час | |
| 32 | 8x4 | 112 | 17час | 406 | 23час |
| 33 | 11x3 | 22 | 20час | 428 | 2дн |
| 35 | 7x5 | 158 | 7дн | 586 | 9дн |
| 36 | 6x6 | 46 | 12дн | 632 | 21дн |
| 9x4 | 69 | 16дн | 701 | 37дн | |
| 12x3 | 20+ | 8дн+ | 720+ | 45дн+ |
Стоит отметить что:
- Генератор работал более 45 дней.
- Задачи до площади 32 были сгенерированы в первый день.
- На поиск задач с площадью 36 ушло 36 дней.
- Неожиданно большое количество задач было найдено для размерностей 8x4 и 7x5: 112 и 158 соответственно. Это значительно больше чем для других размерностей.
Раскраска разбиения
Первые три фильтра оперируют только состояниями граней в виде набора битов. Следующие за ними фильтры оперируют в терминах фигур. Чтобы перевести набор бинарных состояний в набор фигур, используется однопроходный алгоритм раскраски разбиения на отдельные фигуры:
int color = 1;
for(int i = 0; i < H; ++i) {
for(int j = 0; j < W; ++j) {
if (painted[i][j] == 0) {
flood(i, j, color++);
}
}
}
Здесь функция flood закрашивает фигуру, начиная с клетки (i,j), используя очередь смежных клеток, принадлежащих одной фигуре. Общая сложность этого алгоритма раскраски линейна по количеству квадратиков — O(W*H).
Фигуры с вращением
Фигуры, которые можно вращать, ищутся в выбранных для игры разбиениях перебором. Для каждой фигуры рассматривается множество всевозможных её поворотов и отражений — преобразований: 4 поворота и отражение, — всего восемь вариантов. Для Триплекса максимум 4: у палочек по 2, у уголков 4. Если в исходном наборе фигур, одну заменить на любое её преобразование, и при этом из нового набора нельзя составить решение, тогда такую
фигуру можно разрешить поворачивать — решение останется тем же. Далее, из набора поворачиваемых фигур, для игры выбирается одна, которая больше всего усложняет задачу поиска решения Solver-ом. Выбранная фигура случайным образом поворачивается.
Интуитивно кажется, что задачи с поворачиваемыми фигурами легче решать — собираем все фигуры, оставляя свободное место
для поворачиваемой, и потом больше шансов, что фигура влезет в оставленное место. Однако, если учесть, что, делая фигуру
поворачиваемой, мы не добавляем новых решений, то количество комбинаций, которое приходится проверить Solver-у,
увеличивается в такое количество раз, сколько различных преобразований у поворачиваемой фигуры (2 или 4 для Триплекса).
Можно было бы выбрать несколько поворачиваемых фигур, например одно из максимально усложняющих решение подмножество фигур. Возможно в следующих версиях это будет сделано.
Как упорядочены задачи
Solver решает задачи естественным образом, последовательно перебирая возможные комбинации. Решив задачу, Solver присваивает ей уровень сложности — количество выполненных циклов перебора, которое ограничено сверху количеством возможных комбинаций, рассчитываемое по формуле C!/(C1!C2!...Cm!). Задачи Триплекса упорядочены по возрастанию описанного уровня сложности. Такая оценка сложности не совпадает со сложностью, которую испытывает человек. Чтобы оценить, сложность каждой задачи с точки зрения игрока, на сервере ведётся анонимная статистика времени решения каждой задачи. В будущем, я надеюсь, такая статистика позволит упорядочить задачи лучше.
Другие варианты алгоритма генерации
Перебор всевозможных разбиений не единственный возможный способ поиска всех задач, удовлетворяющих условию игры. Можно искать задачи, перебирая всевозможные наборы фигур, по суммарной площади совпадающие с площадью решения. В Триплексе, например, всего 8 различных фигур: две двойных палочки, две тройных палочки и четыре тройных уголка.
Для задачи 6х6=36, максимальное количество фигур 18, минимальное 12. Таким образом, количество наборов можно оценить сверху величиной 818/(2!63!3!) = 248/9 < 245 (каждая из 18-ти фигур может быть одной из 8 возможных, и делённое на минимальное количество перестановок) и снизу 812/(8!4!) > 216 (каждая из 12-ти фигур может быть одной из 8, и делённое на максимальное количество перестановок). Для упорядоченных наборов формулы те же, но только без делителей. С одной стороны упорядоченных вариантов будет больше, но, скорее всего, удастся придумать более оптимальный обход границ.
Можно перебирать всевозможные восьмёрки чисел (a1, a2,… a8), где ai — количество i-тых фигур в решении. Для таких восьмёрок действует линейное ограничение на суммарную площадь фигур:
2*a1 + 2*a2 + 3*a3 + 3*a4 +… + 3*a8 = 36
Программа, работавшая по такому алгоритму, нашла все уровни Триплекса за 2 часа. Это в 500 раз быстрее, чем потребовалось для перебора разбиений. Правда стоит отметить, что сложность возрастает экспоненциально. За следующие две недели такой способ нашел всего 1300 уровней.
Клиентская часть игры
Немаловажную часть игры составляет программа, которая предоставляет игроку возможность решать сгенерированные задачи. Игра написана на языках HTML, CSS и JavaScript (всего 2100 строк). Вся логика, все ресурсы и даже все 700+ уровней уместились в одном html файле. Поэтому, один раз скачав игру, можно пройти её до самого конца, не имея сетевого подключения.
Графический дизайн
Графика в игре очень простая, без картинок, не считая фоновой. Квадратики выполнены в виде разноцветных <div>-ов с градиентной заливкой. Круг внутри вращаемого квадратика — тоже квадратик, только с максимально закруглёнными границами и обратной градиентной заливкой. Оказалось, что в IE9 не предусмотрен такой трюк и градиентная заливка кружка делается всё равно квадратной.
Фон в игре я хотел сделать живым. На нём должны были усыпляющее медленно летать серые круги из дивов. Видимо навеяло оформление HTC Sense. Однако, я наткнулся на два препятствия.
Во-первых: очень плавно заставить их летать не получилось: движение на один пиксель в секунду почему-то выглядело скачкообразно, дёргано. Я пытался сдвигать чаще с шагом меньше 1.0, но сдвигались они всё равно дискретно.
Во-вторых: в некоторых браузерах под Android даже несколько больших кругов очень сильно загружали систему. Поэтому я просто сделал из фона статическую картинку и 'зашил' её внутрь html файла вот таким CSS заклинанием: background-image: url(data:image/png;base64,/9j/4AAQSkZ ...=);
Чтобы размер квадратиков подстраивался под размер и разрешение экрана, я не использовал спрайты, потому что при масштабировании они становятся нечёткими.
Возможно, кто-то спросит, почему я не использовал HTML5 Canvas для 2D графики? Соглашусь, что для такой простой графики функционал Canvas-а подошел бы очень хорошо. Но так получилось, что когда я писал прототип, мне была известна одна неприятная особенность координатной сетки Canvas-а: целочисленные координаты обозначают промежутки между пикселями. К тому же, не внушала оптимизма производительность Canvas-а на моём новеньком планшете. Поэтому первый прототип использовал HTML DOM и квадраты из DIV элементов, которые дожили до окончательной версии.
Сохранение пройденных уровней
Восприятие HTML игр для большинства людей, кому я показывал Триплекс, заставляло их беспокоиться о сохранении результатов прохождения. Обычно они спрашивали где-то на 15-30 уровне: «А если сеть отключится или комп зависнет, то всё заново проходить?»
Наверное важно отметить, что игра автоматически сохраняется каждые 10 секунд в вашем профиле браузера на жестком диске. Поэтому не стоит бояться выключить компьютер или обновить страницу. Механизм сохранения использует HTML5 localStorage. Это, а также то, что все уровни хранятся в самой игре, позволяет играть без сетевого подключения.
Однако у localStorage, есть и обратная сторона медали, которую я обнаружил во время бета тестирования, решив зарегистрировать новое доменное имя и переселить игру на новый адрес. Дело в том, что localStorage привязан к доменному имени сайта. Получается, что если игрок загрузит игру с другого сайта, то придётся начинать всё сначала. Чтобы подойти системно к вопросу, давайте уточним, к чему ещё привязан localStorage. К локальному диску, а значит, на другом устройстве уже не поиграешь (либо на работе, либо дома, ну или на телефоне). Ещё есть привязка к браузеру, мы же не знаем где и в каком формате хранится localStorage. Тут мои руки потянулись к старым добрым проверенным cookies, логинам, паролям и серверной поддержке навороченными скриптами. И пока лень сопротивлялась, было решено прибегнуть к ещё более древнему способу тех времён, когда наших прадедов ещё пацанами оттаскивали зауши от чёрно-белого телевизора и приставки Денди. Да, вы уже догадались, я говорю про запись номера уровня и его кода карандашом на бумажке. Код можно найти в опциях игры.
Интернационализация и локализации
Я обещал своей тёте, что закончу с игрой и она сможет поиграть. Поэтому решил реализовать возможность перевести игру на русский или другой язык. Такая возможность называется интернационализацией, и в кругу разработчиков обозначается i18n, потому что в английском слове internacionalization между первой i и последней n стоят 18 символов.
В голову пришла настолько простая идея реализации i18n, что даже не пришлось искать готовых решений. Для каждого HTML элемента, в котором содержится языковой текст, был указан класс 'i18n'. Например:<span class='i18n'>simple graphics</span>. В коде игры, заведена структура I18N, в которой содержатся переводы всех фраз:
// переводы фраз
var I18N = {
"OK": {
ru: "OK",
fr: "bon",
de: "OK",
zh: "??" },
"simple graphics": {
ru: "простая графика",
fr: "graphiques simple",
de: "einfache Graphik",
zh: "????" },
...
}
При первой смене языка, для всех элементов класса i18n, их оригинальное содержимое сохраняется в поле origHTML и заменяется на перевод, указанный в структуре I18N.
Фраза 'N секунд/минут/часов/дней назад' потребовала контекстнозвисимого перевода. Для этого пришлось немного усложнить логику. В структуре I18N вместо перевода, можно указывать функцию, которая переводит в зависимости от контекста:
"seconds ago": {
en: i18nSecondsAgoEn,
ru: <b>i18nSecondsAgoRu</b>,
fr: " il y a quelques seconds",
de: i18nSecondsAgoDe,
zh: " ???" },
...
function <b>i18nSecondsAgoRu</b>(context) {
return i18nNumberRu(context, 'секунд', 'секунду', 'секунды');
}
...
function i18nNumberRu(context, num0, num1, num2) {
var num = +context;
var result;
if (num >= 20) {
num = num % 10;
}
if (num == 1) {
result = num1;
} else if (2 <= num && num <= 4) {
result = num2;
} else {
result = num0;
}
return context + ' ' + result + ' назад';
}
Русскую локализацию (l10n = localization) делал я сам, французскую, немецкую и китайскую мне сделали друзья: Юля, Маша с Сергеем и Алексей.
Таблица достижений
Для игроков, которым важен соревновательный дух, игра дополнена серверной поддержкой таблицы достижений, которая доступна с главной страницы игры. В таблице достижений для каждого уровня хранится имя игрока, решившего этот уровень первым.
Играя в режиме online:
- все игроки видят, кто и как давно первым решил текущий уровень;
- после прохождения каждого уровня на сервер отправляется время прохождения уровня, и если этот уровень ещё никто не прошел, то можно также занести своё имя в таблицу.
Как взломать игру
Уверен, что найдутся умельцы, которые попытаются записаться в таблицу рекордов, не решая задачи из игры. Хочу сказать, что в лоб это сделать не получится. Чтобы отметить на сервере своё прохождение уровня, надо предоставить контрольную сумму решения. Эта контрольная сумма также нужна, для того чтобы перейти к следующему уровень. То есть, каждый уровень в игре закодирован решением предыдущего.
Я также попытался защитить от взлома серверную часть:
- есть проверки для всех входных параметров;
- экранирование специальных символов в SQL запросах;
- экранирование специальных HTML символов в таблице рекордов.
Легко можно испортить статистику по времени прохождения, но она на игру никак не влияет, и сделана только для приблизительной оценки сложности уровней.
Вопросы подготовки сайта и размещения игры в интернете
Чтобы поделиться игрой не только с друзьями, но и с многочисленной интернет аудиторией, пришлось погрузится в изучение большого числа сопутствующих технологий: , регистрация доменного имени, форумы, социальные сети, web services, openID,… Все эти термины на слуху у большинства пользователей, но даже для того, чтобы просто решить, подходит или нет та или иная технология для решения конкретных задач, приходится изучать её глубже.
Денежный вопрос
Оказалось, что не всё в этом мире можно сделать бесплатно. Пока затраты на игру довольно скромные: 150 руб/год за доменное имя, 300 руб/год за простенький
Заключение
Ну вот вроде бы и всё, о чём пока нашлось время рассказать. Надеюсь игра вам понравится настолько, насколько мне было интересно её создавать.
Заходите на форум www.quadpuzzle.ru/forum или пишите письма TriplexQuad@gmail.com. Буду рад любым вашим комментариям.
Автор: yrouban