Деревянные вопросы
Не знаю, одному мне так везёт, или нет, но буквально на каждом собеседовании на позицию BE разработчика я слышал и продолжаю слышать вопрос про индексы в реляционных СУБД. Затем речь часто заходит про "а что там под капотом?", и, как правило, сходу вспоминаются B-Tree и Hash, причём первый - это дефолт и собственно то, что мы чаще всего видим. Ну Hash это конечно Hash Map, да и с B-Tree по названию вроде всё логично и понятно: Tree в названии однозначно указывает на дерево, ну а В это, конечно, Binary? Или Balanced? Или Balanced Binary? Почему-то долгое время я полагал, что это Balanced Binary, и эта версия даже "прокатывала".
На самом деле Binary здесь, конечно, лишнее. B-Tree сбалансированное дерево поиска, но никак не бинарное. В статье я постараюсь привести базовую идею этой структуры, его преимущества и примеры использования. Для иллюстрации рассуждений также реализую Set с B-Tree под капотом на Java и сравню его с родным TreeSet (который в свою очередь "под капотом" имеет как раз таки бинарное Red-Black Tree).
TL;DR
Сухой итог
BTree - это дерево поиска, в каждом узле которого содержится множество ключей и поддеревьев ( буквально от 2 и до тысяч на практике). У него есть две киллер-фичи, которые в подавляющем большинстве ситуаций и делают его золотым стандартом для реализации индексов в СУБД:
-
Сбалансированность из коробки просто в силу самого алгоритма добавления (с удалением не так всё просто, но тоже можно "порешать вопросики", хоть и не бесплатно)
-
За счёт низкой высоты дерева требуется относительно малое число случайных чтений, зато больше последовательных. Это чрезвычайно уместно, если наши данные не умещаются в памяти и часть индекса (или вообще весь индекс) лежит в файловой системе или ином медленном хранилище
Для иллюстрации я реализовал Set с базовым функционалом (add/remove/contains) на основе B-Tree и сравнил его с родным TreeSet. По производительности B-Tree чуть выигрывает на небольших наборах данных, вероятно за счёт меньшего числа чтений из памяти, либо за счёт отсутствия какого-то оверхеда, но ситуация меняется по мере роста деревьев. Подробности ниже по тексту, код на гитхабе.
А чего сразу куст-то?
В "нормальных" бинарных деревьях новые ключи добавляются как листья к существующему дереву. За счёт этих новых листьев и увеличивается высота дерева. Ширина при этом растёт не особо быстро: если мы "вкормим" в дерево ключей, то ширина уровня листьев при идеальной балансировке будет на уровне
, а его высота -
. Для
порядка миллиона мы должны получить ширину ~500к листьев и высоту ~20 уровней. Чтобы у дерева "отрос" ещё уровень листьев нам нужно докинуть столько же ключей, сколько в нём уже есть, для нашего примера - ещё миллион.
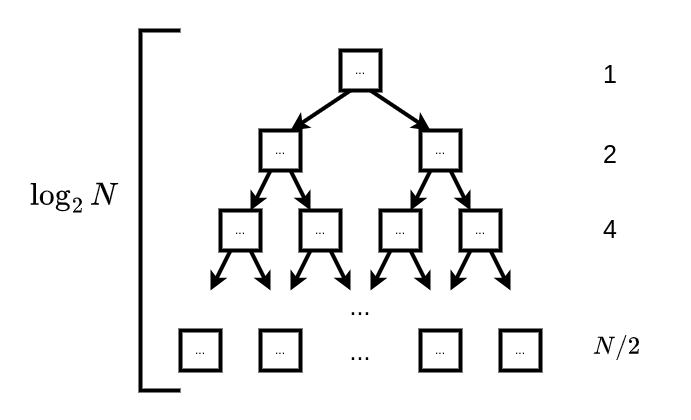
В B-Tree у каждого узла вместо 1 ключа и 2 потомков есть множество ключей и потомков. B-Tree характеризуется таким параметром как : корень содержит от 0 до
ключей, а любой другой узел - от
до
; у любого узла либо 0 потомков (тогда это лист), либо
где
- количество ключей в этом узле.

Получается, что этот самый (далее
) ощутимо влияет на рост высоты дерева: при "вкармливании" в него
ключей мы получим дерево высотой не более
. Для примера рассмотрим B-Tree с
(нет, я не буду его рисовать). Вкормив в него тот же миллион неудачных ключей (таких, что в каждом узле будет всего по 100 ключей, хотя в среднем их будет от 100 до 200) мы получим на последнем уровне около 990к ключей, раскиданные по ~10k листьев. Высота такого дерева составит всего 3 уровня и на первых двух уровнях будут суммарно всего ~10к ключей (у бинарного для сравнения там же оказалась бы половина ключей, т.е. ~500к). Теперь чтобы у нашего B-Tree отрос полный четвёртый уровень нам нужно добавить
раз столько же элементов, сколько в нём лежит - т.е. для примера с
- 100млн. А ещё уровень - это уже 10млрд. При увеличении
пример становится ещё более унизительным.
Ну что, куст же?
Именно за счёт малой высоты B-Tree с большими значениями находит применение в базах данных: при высоте дерева в
уровней на первых
уровнях содержится не более
узлов. Это позволяет умещать первые уровни дерева в памяти и делать всего один запрос к файловой системе уже на последнем этапе поиска.
Преимущество подхода несложно видеть даже на примере ниже, хотя там он несколько вырожденный: поищем в этом дереве ключ , для B-Tree это делается в 2 чтения из памяти, тогда как для аналогичного бинарного дерева - 5. Чем дороже операция чтения, тем больше пользы от большого
.

Конечно это не единственный плюс B-Tree для баз данных, да и вообще, я описал сильно упрощённый вариант, на хабре есть отличная статья по реализации B-Tree индексов в Postgres: Индексы в PostgreSQL — 4. Там и про отношения между узлами одного уровня (двусвязный список), и про удобство для выборки интервала ключей, и про связь с размером страницы памяти, и про проблемы этой структуры, которых, впрочем, не избегу и я далее по тексту.
Это далеко не новая тема, возможно читателю больше понравится объяснение структуры в лекциях CMU или Вики ИТМО или в «Алгоритмы. Построение и анализ» Т.Кормена. Остаток же этой статьи я оставлю для реализации BTree на Java. Почему Java? Мне хотелось вспомнить, как на нём вообще писать, так что это больше тренировочная реализация, ну и к тому же в Java есть родной TreeSet, с которым можно сравнить время выполнения операций. Гоняться со стандартной библиотекой - это, конечно, пустое, но можно хотя бы поверхностно оценить производительность алгоритмов.
Агрономика
Посадка
Наше дерево начнётся с корня, поэтому просто создаём его.
public class BTreeSet<E> {
static public class Node {
public Object[] values;
public Node[] children;
public int valuesCount;
public int childrenCount;
public Node(Object[] values, Node[] children, int valuesCount, int childrenCount) {
this.values = values;
this.children = children;
this.valuesCount = valuesCount;
this.childrenCount = childrenCount;
}
public boolean hasChildren() {
return childrenCount > 0;
}
}
private int size;
private int valuesMaxSize;
private int childrenMaxSize;
private Node root;
private Comparator<E> comparator;
public BTreeSet(Comparator<E> comparator) {
this(2, comparator);
}
public BTreeSet(int factor, Comparator<E> comparator) {
this.size = 0;
this.comparator = comparator;
this.valuesMaxSize = 2 * factor;
this.childrenMaxSize = 2 * factor + 1;
this.root = new Node(
new Object[valuesMaxSize],
new Node[childrenMaxSize],
0,
0
);
}
}Подкормка
В бинарном дереве новые ключи добавляются в качестве потомков существующих листьев, а в B-Tree это устроено немного иначе: мы докидываем ключи в один из существующих листьев, а когда тот вырастает слишком большим, то должен разделиться!
Добавление ключа
Добавление ключа тривиально - используя операции сравнения пройдём дерево до листа, в который должен быть помещён ключ, а затем вставим его, соблюдая сортировку (ключи в узле сортированы по возрастанию).
public boolean add(E value) {
return add(value, root, null);
}
private boolean add(E value, Node node, Node parent) {
int newValuePosition = findPositionForValueInNode(value, node);
if (newValuePosition < node.valuesCount && compare(value, (E)node.values[newValuePosition]) == 0) {
// Value already present, return false on attempt to duplicate it
return false;
} else if (node.hasChildren()) {
// Not a leaf node, we should go further down the tree
return add(value, node.children[newValuePosition], node);
} else {
// A leaf node, we should put value here
insertValueInArray((Object[])node.values, node.valuesCount, value, newValuePosition);
this.size++;
node.valuesCount++;
return true;
}
}Нереализованные функции
findPositionForValueInNodeпока реализовывать не будем, предположим, что она будет делать ровно то, что указано в названии - искать индекс для данного value в узле. Аналогично insertValueInArray готовит место и впихивает данное ей value в массив, её вообще приводить не интересно.
Деление узла
По мере добавления новых ключей в дерево происходит заполнение листьев. Когда в листе оказывается максимальное число ключей, он делится на два: выбирается "опорный" ключ, все ключи меньше него оказываются в левом новом листе, а больше - в правом, сам же опорный ключ отправляется в родительский узел. В своей реализации я беру опорный ключ буквально из середины массива, но в практическом применении может выбираться что-то более оптимальное, например Postgres имеет некоторый алгоритм (линейная интерполяция?) выбора этого ключа для минимизации пустого места в дереве.

private Node splitNode(Node sourceNode, Node parent, E value) {
int middleIndex = valuesMaxSize / 2;
E middleValue = (E)sourceNode.values[middleIndex];
Node leftNode = new Node(
copyOfRangeWithSize(sourceNode.values, 0, middleIndex - 1, valuesMaxSize),
copyOfRangeWithSize(sourceNode.children, 0, middleIndex, childrenMaxSize),
middleIndex,
sourceNode.childrenCount > 0 ? middleIndex + 1 : 0
);
Node rightNode = new Node(
copyOfRangeWithSize(sourceNode.values, middleIndex + 1, valuesMaxSize - 1, valuesMaxSize),
copyOfRangeWithSize(sourceNode.children, middleIndex + 1, childrenMaxSize - 1, childrenMaxSize),
valuesMaxSize - middleIndex - 1,
sourceNode.childrenCount > 0 ? childrenMaxSize - middleIndex - 1 : 0
);
if (parent == null) {
// Node is root and it is full -> split it and have new root
// Do it in place
sourceNode.values = (E[]) new Object[valuesMaxSize];
sourceNode.children = new Node[childrenMaxSize];
sourceNode.values[0] = middleValue;
sourceNode.valuesCount = 1;
sourceNode.children[0] = leftNode;
sourceNode.children[1] = rightNode;
sourceNode.childrenCount = 2;
return sourceNode;
} else {
// Push middle value with new subnodes to parent
pushValueWithChildrenToNode(parent, middleValue, leftNode, rightNode);
return parent;
}
}Нереализованные функции
copyOfRangeWithSize здесь - это аналог Arrays.copyOfRange , единственное отличие - размер результата берётся не по размеру копируемого интервала, а передаётся аргументом.
Я уже упоминал, что опорный ключ отправляется в родительский узел, но что если тот заполнен? Чтобы избежать этого я буду проверять текущий узел на переполнение и делить его на всём пути спуска до листьев. Это гарантирует, что в родителе всегда есть место для опорного ключа, если потребуется разделить узел ниже по ходу поиска. Это не единственный вариант реализации деления, есть альтернативные алгоритмы.

private boolean add(E value, Node node, Node parent) {
if (node.valuesCount >= valuesMaxSize) {
node = splitNode(node, parent, value);
}
int newValuePosition = findPositionForValueInNode(value, node);
// ...
}Сезонная обрезка
Удаление ключа из листа достаточно тривиально - мы просто "схлопываем" элементы вокруг удаляемого и в общем-то всё.
Всё несколько сложнее, если удаление происходит из корня или промежуточного узла: просто удалив ключ мы сломаем контракт дерева, ведь у узла остались потомки, которые связаны с ним. Чтобы дерево продолжало функционировать, нужно "стащить" у кого-то новый ключ на место старого. И желательно сделать это с минимальным влиянием на дерево - читай "не трогать потомков". Для этого можно взять либо максимальный ключ левого относительно удалённого ключа поддерева, либо минимальный ключ правого поддерева. Есть более изощрённные способы разрешения ситуации, но в текущей реализации я буду именно тащить максимальный элемент левого поддерева.
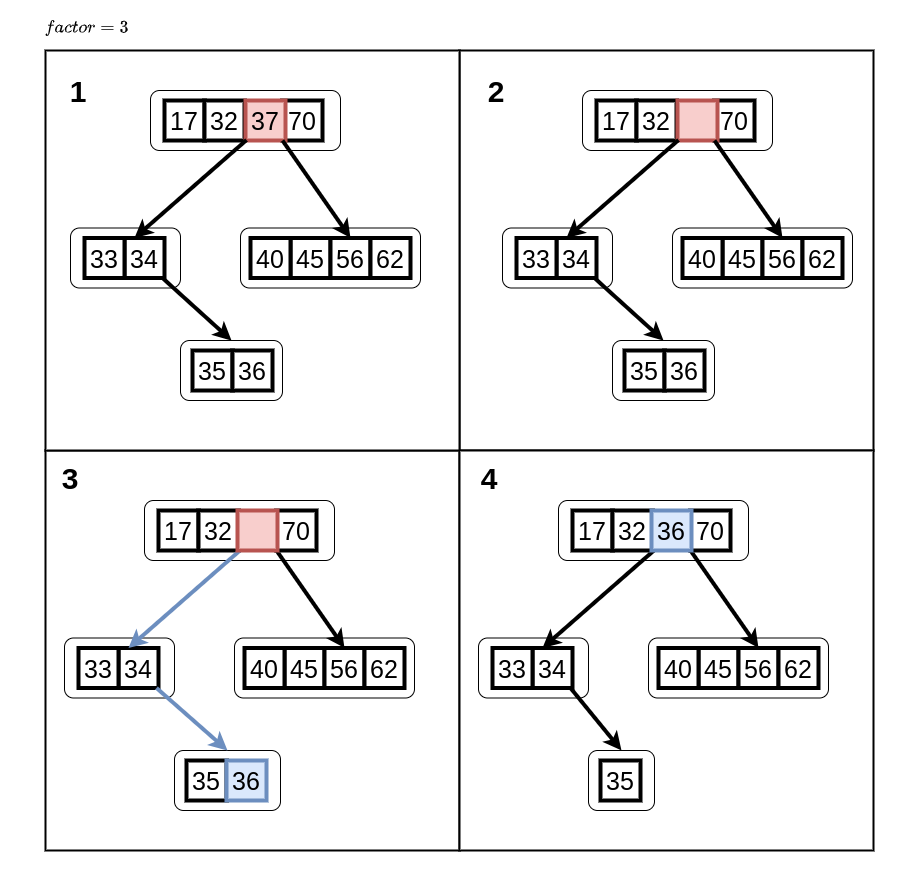
В процессе удаления может сложиться ситуация, когда в листе не остаётся ключей - в промежуточных узлах такого не случится, т.к. они постоянно тянут новые ключи из листьев. При этом напрямую грохнуть пустой лист нельзя - сломается порядок потомков его родителя. Но вот если мы будем удалять в родителе ключ, относящийся к этому потомку, то тут можно и развернуться - удалить и ключ и соответствующего потомка.

Теперь можно писать код, для удаление его что-то больше всего получилось. И это всего лишь "наивное" удаление без слияния узлов, переноса ключей между узлами одного уровня и прочих фич:
public boolean remove(E value) {
return remove(value, root);
}
private boolean remove(E value, Node node) {
int position = findPositionForValueInNode(value, node);
if (position < node.valuesCount && compare(value, (E)node.values[position]) == 0) {
// Found element, should remove it now
removeValueFromNodeByIndex(node, position);
return true;
}
// We are at the leaf and didn't find element yet. It means it's not in the tree
if (!node.hasChildren()) return false;
return remove(value, node.children[position]);
}
private void removeValueFromNodeByIndex(Node node, int index) {
this.size--;
if (node.childrenCount == 0) {
// If no children, simply drop the value by copying array without it
System.arraycopy(node.values, index + 1, node.values, index, node.valuesCount - index - 1);
node.valuesCount--;
return;
}
// Need to find replacement for value in children
Node replacementNode = node.children[index];
Object newValue = extractMaxKeyFromSubtree(replacementNode);
if (newValue == null) {
// Corresponding child is already empty so there's no replacement -> we should simply drop current value and child together
System.arraycopy(node.values, index + 1, node.values, index, node.valuesCount - index - 1);
System.arraycopy(node.children, index + 1, node.children, index, node.childrenCount - index - 1);
node.valuesCount--;
node.childrenCount--;
} else {
// There was a replacement in the leaf - should put it into place of removed key
node.values[index] = newValue;
}
}
private Object extractMaxKeyFromSubtree(Node subtree) {
Object result = null;
if (subtree.hasChildren()) {
// Try to get max from right subtree first
result = extractMaxKeyFromSubtree(subtree.children[subtree.childrenCount - 1]);
}
if (result == null && subtree.valuesCount > 0) {
// If right subtree is already empty, max key is the rightmost one in current node
subtree.valuesCount--;
result = subtree.values[subtree.valuesCount];
if (subtree.hasChildren()) {
// Right subtree is empty and we're extracting max key from current node, can drop the child too
subtree.childrenCount--;
}
}
return result;
}Коммунальная обрезка
Несложно видеть, что удаляя ключи мы можем столкнуться с глубоко неоптимальным деревом - в некоторых узлах могут остаться мало ключей (меньше , что вообще плоховато), в каких-то вообще нисколько. В вырожденном случае весь нижний уровень (а он самый большой) может оказаться пустым.

Есть несколько вариантов по улучшению ситуации, в текущуй реализации я добавляю слияние узлов - если после удаления ключа из узла этот узел вместе с одним из соседей содержит меньше максимального кол-ва ключей, то производится процедура обратная разделению (split). Код привожу под спойлером ниже.
Слияние узлов
private boolean remove(Object value, Node node, Node parent, int positionInParent) {
int position = findPositionForValueInNode((E)value, node);
if (position < node.valuesCount && compare((E)value, (E)node.values[position]) == 0) {
// found element, should remove it now
removeValueFromNodeByIndex(node, position);
return true;
}
// We are at the leaf and didn't find element yet. It means it's not in the tree
if (node.childrenCount == 0) {
return false;
}
boolean result = remove(value, node.children[position], node, position);
if (result) {
// Try to merge with right or left neighbour after removing a key
tryMergeNeighbours(node.children[position], node, position);
// The tree may end up in a situation when its root has no keys and only one child
// in such case we should compact it (place the only child in root's place)
if (parent == null) compactNode(node);
}
return result;
}
// The tree may end up in a situation when its root has no keys and only one child
// in such case we should compact it (place the only child in root's place)
private void compactNode(Node node) {
while (node.valuesCount == 0 && node.hasChildren()) {
Node child = node.children[0];
node.values = child.values;
node.valuesCount = child.valuesCount;
node.children = child.children;
node.childrenCount = child.childrenCount;
}
}
// Try to merge with right or left neighbour
// returns result of the merge or node itself
private Node tryMergeNeighbours(Node node, Node parent, int indexInParent) {
if (indexInParent > 0) {
Node leftNeighbour = parent.children[indexInParent - 1];
int newNodeValuesCount = leftNeighbour.valuesCount + node.valuesCount + 1;
if (newNodeValuesCount < valuesMaxSize) {
mergeNodes(leftNeighbour, node, parent, indexInParent - 1);
return leftNeighbour;
}
}
if (indexInParent + 1 < parent.childrenCount) {
Node rightNeighbour = parent.children[indexInParent + 1];
int newNodeValuesCount = rightNeighbour.valuesCount + node.valuesCount + 1;
if (newNodeValuesCount < valuesMaxSize) {
mergeNodes(node, rightNeighbour, parent, indexInParent);
return node;
}
}
return node;
}
private void mergeNodes(Node left, Node right, Node parent, int leftPosition) {
int rightPosition = leftPosition + 1;
int nextAfterRightPosition = rightPosition + 1;
// Put middle element back (opposite to split)
left.values[left.valuesCount] = parent.values[leftPosition];
left.valuesCount++;
// Copy values from right node
System.arraycopy(right.values, 0, left.values, left.valuesCount, right.valuesCount);
left.valuesCount += right.valuesCount;
if (left.hasChildren()) {
System.arraycopy(right.children, 0, left.children, left.childrenCount, right.childrenCount);
left.childrenCount += right.childrenCount;
}
// We perform merge not at the end of parent's children list
// and therefore should copy over the elements after merged ones
if (leftPosition < parent.valuesCount - 1) {
System.arraycopy(parent.values, rightPosition, parent.values, leftPosition, parent.valuesCount - rightPosition);
System.arraycopy(parent.children, nextAfterRightPosition, parent.children, rightPosition, parent.childrenCount - nextAfterRightPosition);
}
parent.valuesCount--;
parent.childrenCount--;
}В чём-то похожая проблема есть, кстати, и в индексах Postgres - она обсуждалась здесь и предложенное решение - перестроить индекс. Так что перестроение в такой ситуации может быть неплохой альтернативой. Ну или делать то, что делают коммунальщики - подождать (читай накидать в него ещё ключей), авось само обрастёт обратно.
Сбор
Ну наконец то, ради чего всё затевалось: поиск!
В процессе давнего обсуждения с коллегой я услышал, что B-Tree был бы медленным за счёт большого числа ключей в ноде. Этот разговор во многом побудил меня написать эту статьи, поэтому сначала я приведу алгоритм поиска ключа в узле простым перебором (тот самый findPositionForValueInNode, реализацию которого я отложил). На этом этапе дерево должно быть уже вполне рабочим и я могу уже сравнить его производительность с родным TreeSet.
public boolean contains(E value) {
return contains(value, root);
}
private boolean contains(E value, Node node) {
int position = findPositionForValueInNode(value, node);
// Found it!
if (position < node.valuesCount && compare(value, (E)node.values[position]) == 0) return true;
// We are at the leaf and didn't find element yet. It means it's not in the tree
if (!node.hasChildren()) return false;
return recursiveContains(value, node.children[position]);
}
private int findPositionForValueInNode(E value, Node node) {
int newValuePosition = node.valuesCount;
// Empty node - either root at the start or some weird node after removal
if (newValuePosition == 0) return 0;
while (newValuePosition > 0) {
int compareResult = compare((E)node.values[newValuePosition - 1], value);
// Found element itself, should return its position
if (compareResult == 0) return newValuePosition - 1;
// Left element is smaller than current one - should insert current one on current place
if (compareResult < 0) return newValuePosition;
newValuePosition -= 1;
}
return newValuePosition;
}С поиском в узле перебором в худшем случае мы получим сложность поиска , где
- фактор дерева,
- кол-во ключей. Это получается просто в силу того, что для гарантированного нахождения ключа нужно пройти всё дерево по высоте (а высота дерева не более
) и в каждом из узлов проверить от 1 до
ключей. С точки зрения алгоритмической сложности у нас вообще получается
:
это вообще константы, кто их считает? Ок, время сравнить с TreeSet, пока только поиск:
Бенчмарки
Для сравнения я использую родной Java TreeSet и 3 варианта BTree - с (
тоже пробовал, но это прямо таки совсем бессмысленно с точки зрения практического применения). Для сравнения в деревья добавляются 100к случайных ключей от 0 до 100000, затем удаляются 50к случайных ключей из того же диапазона. Я рассчитываю, что это в разумном объёме прореживает дерево, чтобы как-то эмулировать реальное применение. Затем для замера скорости проводится поискдобавлениеудаление 10к ключей из тех, что были добавлены в начале (часть должна была удалиться, т.е. уже не представлены в дереве).
Так же позднее добавил бенчмарки на случайных строках lorem ipsum - здесь гипотеза такая, что на более тяжёлом компараторе может проиграть алгоритм, требующий больше сравнений (в то числе на константу больше). Их привожу позднее.
Код бенчмарков на гитхабе. Это часть, которая оказалась сложнее самой реализации дерева и написания этой портянки текста. Я мог сделать ошибки. Я буду благодарен, если кто-нибудь на них укажет.
Benchmark Mode Cnt Score Error Units
LookupBenchmark.BTree3 ss 20 4334220.950 ± 283045.902 ns/op
LookupBenchmark.BTree10 ss 20 3537762.900 ± 249627.362 ns/op
LookupBenchmark.BTree100 ss 20 5030886.900 ± 372271.905 ns/op
LookupBenchmark.BTree1000 ss 20 19278231.300 ± 2759189.556 ns/op
LookupBenchmark.JavaTree ss 20 3735875.200 ± 369086.499 ns/opНу ладно, предсказуемо, зависимость от не совсем линейная, возможно из-за малого числа элементов в нодах дерева с
. Можно для сравнения переписывать на бинарный поиск. Его асимптотическая сложность должна быть уже
т.е. не зависеть от
и равняться таковой у бинарного дерева с точностью до константы.
private int findPositionForValueInNode(E value, Node node) {
int upperBound = node.valuesCount - 1;
int lowerBound = 0;
int currentPosition;
while (upperBound >= lowerBound) {
currentPosition = (upperBound + lowerBound) / 2;
int compareResult = compare((E)node.values[currentPosition], value);
if (compareResult == 0) {
// Found it!
return currentPosition;
} else if (compareResult > 0) {
upperBound = currentPosition - 1;
} else {
lowerBound = currentPosition + 1;
}
}
return lowerBound;
}И результаты:
Benchmark Mode Cnt Score Error Units
LookupBenchmark.BTree3 ss 20 4980452.300 ± 363053.540 ns/op
LookupBenchmark.BTree10 ss 20 4144964.350 ± 147929.751 ns/op
LookupBenchmark.BTree100 ss 20 3910115.600 ± 209279.402 ns/op
LookupBenchmark.BTree1000 ss 20 3704128.850 ± 256023.934 ns/op
LookupBenchmark.JavaTree ss 20 3692234.700 ± 282524.163 ns/opНу вот, ситуация стала повеселее для больших . С другой стороны похоже, что бинарный поиск не имеет смысла для малых
, видимо он добавляет оверхед по сравнению с простым перебором, что не особо удивительно. В коде напрашиваются достаточно много оптимизаций, но пока можно зафиксировать промежуточные результаты: поиск по производительности похож на поиск по "настоящему" дереву, уже что-то.
Оптимизация
Сразу просматриваются несколько очевидных оптимизаций, которые стоит сделать. Код приводить тоже не буду, только рассуждения, при желании можно посмотреть итог в репозитории.
Срезаем мелочи и не совсем
Первой под нож пойдёт хвостовая рекурсия, где возможно, чтобы не забивать стек? Переписываю add/contains в циклы:
Benchmark Mode Cnt Score Error Units
LookupBenchmark.BTree3 ss 20 4859216.500 ± 392641.181 ns/op
LookupBenchmark.BTree10 ss 20 4070638.950 ± 351575.736 ns/op
LookupBenchmark.BTree100 ss 20 3741470.600 ± 225125.411 ns/op
LookupBenchmark.BTree1000 ss 20 3440761.200 ± 176463.944 ns/op
LookupBenchmark.JavaTree ss 20 3681791.900 ± 294030.188 ns/opС некоторым допущением можно сказать, что что-то стало лучше.
Следующим шагом проверим, сделала ли Java очевидную вещь - замену деления на 2 на сдвиг, меняю эти места вручную. И увеличиваю кол-во замеров, а то за +- 10% плохо видно. И добавляю строки.
Benchmark(Integer) Mode Cnt Score Error Units
LookupBenchmark.BTree3 ss 100 4733719.510 ± 145137.425 ns/op
LookupBenchmark.BTree10 ss 100 4042940.730 ± 134647.100 ns/op
LookupBenchmark.BTree100 ss 100 3527921.220 ± 94431.726 ns/op
LookupBenchmark.BTree1000 ss 100 3538251.700 ± 80785.712 ns/op
LookupBenchmark.JavaTree ss 100 3750000.300 ± 126217.465 ns/op
Benchmark(String) Mode Cnt Score Error Units
LookupStringsBenchmark.BTree3 ss 100 8560899.970 ± 200320.505 ns/op
LookupStringsBenchmark.BTree10 ss 100 7846474.900 ± 191177.261 ns/op
LookupStringsBenchmark.BTree100 ss 100 7277645.230 ± 159630.210 ns/op
LookupStringsBenchmark.BTree1000 ss 100 7024600.330 ± 158602.701 ns/op
LookupStringsBenchmark.JavaTree ss 100 7455433.920 ± 299656.742 ns/op ns/opНа вид стало лучше. Может Java и не оптимизировала этот момент. А может стоило ранее не жлобиться и сразу делать 100 итераций, чтобы погрешность была меньше. Кто ж теперь узнает. Оставляю так.
Память
Даже без удаления узлы в нормальном состоянии дерева могут быть не совсем заполнены, то есть в нём точно есть лишняя выделенная память, но как оно выглядит на реальном примере? Попробуем построить дерево с из 100к рандомных ключей и посмотреть, насколько всё плохо. Чтобы сделать ситуацию хуже, добьёмся получения этого дерева через последовательное добавление 100к случайных ключей, а затем удаление 80к из них, а потом снова добавление и снова удаление... И так пока не наберётся как минимум (больше можно) 100к ключей в дереве.
В эксперименте получилось по 111023 ключа. Теперь в B-Tree есть 2752 узлов на 4 уровнях (1, 2, 63 и 2686 узлов на каждом уровне соответственно), видно, что уровни несколько отличаются от оптимальных (1, 61, 3721, ...). Для каждого из узлов храним 2 инта, 2 указателя и два массива суммарно на 121 указатель (). Считая всё по 4 байта получаем
. А у обычного дерева (считая каждый узел как 3 указателя - на значение, на левое поддерево и на правое поддерево) -
. Немного лучше. Но если присмотреться, то видно, что в текущей реализации B-Tree для всех листов превентивно выделена память под потомков, но их нет. И нет буквально никаких шансов, что они появятся - рост дерева идёт вверх, его нижний уровень всегда остаётся на месте. Если срезать эти излишки, то получится всего
, что внезапно ощутимо меньше, чем у бинарного. Вот теперь точно всё. Как обычно вношу изменения в код на гитхабе, но не привожу здесь.
Расчёт достаточно примитивен и не включает object header и выравнивание. С ними меньшее число узлов оказывается ещё экономнее.
А чего это с памятью так получилось?
Господи Иисусе, кто-то дочитал до этого места и открыл спойлер внутри спойлера? Спасибо! Теперь про память:
Возвращаясь к началу статьи - в бинарном дереве примерно половина узлов - листья, не имеющие потомков, но всё ещё имеющие указатели на них с nullвнутри. То есть указателей "простаивают", но избавиться от них нельзя буквально никак, потому что даже в виде
null это признак отсутствия потомков. В B-Tree в свою очередь простаивают целые массивы указателей на ключи и потомков в узлах, где этих ключей и потомков немаксимальное количество. Но похоже, что это всё равно эффективнее.
Количество сравнений и его зависимость от размера дерева
Предлагаю посмотреть сколько сравнений требует поиск строк в дереве. Суть как в бенчмарках: запихиваем в дерево строк, удаляем
из них и после этого ищем 10000 ключей, часть из которых в дереве есть, а части нету. Ну и считаем вызовы компаратора
comparator.compare(...) :
Comparisons made to find 10000 keys in tree of 4994 keys.
Comparisons count for BTree(factor 3): 121580; average 12.158
Comparisons count for BTree(factor 10): 120019; average 12.0019
Comparisons count for BTree(factor 100): 119264; average 11.9264
Comparisons count for BTree(factor 1000): 118606; average 11.8606
Comparisons count for Java Set: 119107; average 11.9107
Comparisons made to find 10000 keys in tree of 504878 keys.
Comparisons count for BTree(factor 3): 178070; average 17.807
Comparisons count for BTree(factor 10): 183280; average 18.328
Comparisons count for BTree(factor 100): 185556; average 18.5556
Comparisons count for BTree(factor 1000): 186196; average 18.6196
Comparisons count for Java Set: 164735; average 16.4735
Comparisons made to find 10000 keys in tree of 5503622 keys.
Comparisons count for BTree(factor 3): 208744; average 20.8744
Comparisons count for BTree(factor 10): 218451; average 21.8451
Comparisons count for BTree(factor 100): 222054; average 22.2054
Comparisons count for BTree(factor 1000): 221212; average 22.1212
Comparisons count for Java Set: 184874; average 18.4874Похоже, что дерево из стандартной библиотеки значительно экономнее в плане сравнений. Причём разрыв растёт с ростом числа элементов, видно, что количество сравнений в B-Tree почти точно равно , но в Java Set оно ещё лучше, например
, а сравнений в среднем получилось всего 18.5... Наверное по мере роста дерева у TreeSet будет преимущество, надо добавить бенчмарки на бОльшем датасете. А пока подбить итог:
Вжух! И на том же бенчмарке получаем
Benchmark Mode Cnt Score Error Units
LookupBenchmark.BTree3 ss 100 4491093.760 ± 113824.168 ns/op
LookupBenchmark.BTree10 ss 100 3955657.280 ± 104259.518 ns/op
LookupBenchmark.BTree100 ss 100 3531611.410 ± 90054.955 ns/op
LookupBenchmark.BTree1000 ss 100 3398888.750 ± 98544.199 ns/op
LookupBenchmark.JavaTree ss 100 3620823.050 ± 118513.632 ns/opДля небольшого стало только хуже, а остальные скинули по... ерунду какую-то короче. И в среднем оказались на уровне TreeSet. Так что время подводить итоги.
Контрольный забег
Для подведения итогов посмотрим на относительную производительность всех операций - добавления, поиска, удаления. Кроме того добавим поиск в деревьях большего размера (~500k и ~5kk ключей).
Результаты
Результаты на деревьях порядка 50к ключей
Benchmark Mode Cnt Score Error Units
InsertBenchmark.BTree3 ss 100 4722088.220 ± 157640.269 ns/op
InsertBenchmark.BTree10 ss 100 4137478.610 ± 133454.131 ns/op
InsertBenchmark.BTree100 ss 100 4670246.540 ± 688544.369 ns/op
InsertBenchmark.BTree1000 ss 100 4130470.990 ± 90276.965 ns/op
InsertBenchmark.JavaTree ss 100 3848856.180 ± 123844.692 ns/op
LookupBenchmark.BTree3 ss 100 4491093.760 ± 113824.168 ns/op
LookupBenchmark.BTree10 ss 100 3955657.280 ± 104259.518 ns/op
LookupBenchmark.BTree100 ss 100 3531611.410 ± 90054.955 ns/op
LookupBenchmark.BTree1000 ss 100 3398888.750 ± 98544.199 ns/op
LookupBenchmark.JavaTree ss 100 3620823.050 ± 118513.632 ns/op
RemoveBenchmark.BTree3 ss 100 5626406.130 ± 125189.484 ns/op
RemoveBenchmark.BTree10 ss 100 4377464.160 ± 102839.509 ns/op
RemoveBenchmark.BTree100 ss 100 4154719.920 ± 97029.662 ns/op
RemoveBenchmark.BTree1000 ss 100 4339840.950 ± 109503.543 ns/op
RemoveBenchmark.JavaTree ss 100 4855598.190 ± 155505.945 ns/op
Benchmark(String) Mode Cnt Score Error Units
InsertStringsBenchmark.BTree3 ss 100 8187217.570 ± 173368.157 ns/op
InsertStringsBenchmark.BTree10 ss 100 7752785.470 ± 592271.297 ns/op
InsertStringsBenchmark.BTree100 ss 100 7253840.100 ± 165826.517 ns/op
InsertStringsBenchmark.BTree1000 ss 100 7348469.990 ± 127354.334 ns/op
InsertStringsBenchmark.JavaTree ss 100 7404469.400 ± 177941.481 ns/op
LookupStringsBenchmark.BTree3 ss 100 7909663.710 ± 213347.661 ns/op
LookupStringsBenchmark.BTree10 ss 100 6646783.480 ± 129974.960 ns/op
LookupStringsBenchmark.BTree100 ss 100 6510030.450 ± 150733.755 ns/op
LookupStringsBenchmark.BTree1000 ss 100 6088266.120 ± 114544.077 ns/op
LookupStringsBenchmark.JavaTree ss 100 7195944.640 ± 211249.082 ns/op
RemoveStringsBenchmark.BTree3 ss 100 8548929.690 ± 170164.580 ns/op
RemoveStringsBenchmark.BTree10 ss 100 7227995.580 ± 158598.243 ns/op
RemoveStringsBenchmark.BTree100 ss 100 6958251.130 ± 139552.609 ns/op
RemoveStringsBenchmark.BTree1000 ss 100 7263921.030 ± 133818.723 ns/op
RemoveStringsBenchmark.JavaTree ss 100 8508606.270 ± 389131.820 ns/op
Результаты для деревьев большего размера
Просто Lookup - ~50k ключей
Big - ~500k ключей
Huge - ~5kk ключей
Benchmark(Integer) Mode Cnt Score Error Units
LookupBenchmark.BTree3 ss 10 4522873.600 ± 407118.526 ns/op
LookupBenchmark.BTree10 ss 10 4110355.700 ± 347475.903 ns/op
LookupBenchmark.BTree100 ss 10 3583114.100 ± 604730.934 ns/op
LookupBenchmark.BTree1000 ss 10 3461063.700 ± 435177.529 ns/op
LookupBenchmark.JavaTree ss 10 3754289.300 ± 491147.526 ns/op
LookupBenchmark.BigBTree3 ss 10 8649725.900 ± 1369897.170 ns/op
LookupBenchmark.BigBTree10 ss 10 8080699.300 ± 1744388.993 ns/op
LookupBenchmark.BigBTree100 ss 10 6859515.600 ± 1085416.523 ns/op
LookupBenchmark.BigBTree1000 ss 10 6827167.600 ± 863958.634 ns/op
LookupBenchmark.BigJavaTree ss 10 6658629.000 ± 1700001.580 ns/op
LookupBenchmark.HugeBTree3 ss 10 13026209.100 ± 566916.686 ns/op
LookupBenchmark.HugeBTree10 ss 10 11352643.700 ± 903485.703 ns/op
LookupBenchmark.HugeBTree100 ss 10 11106332.400 ± 606793.337 ns/op
LookupBenchmark.HugeBTree1000 ss 10 11736421.900 ± 859256.011 ns/op
LookupBenchmark.HugeJavaTree ss 10 9228314.500 ± 539060.601 ns/op
Benchmark(String) Mode Cnt Score Error Units
LookupStringsBenchmark.BTree3 ss 10 7521619.800 ± 595459.641 ns/op
LookupStringsBenchmark.BTree10 ss 10 6895826.100 ± 293621.419 ns/op
LookupStringsBenchmark.BTree100 ss 10 6410657.800 ± 544833.272 ns/op
LookupStringsBenchmark.BTree1000 ss 10 6103261.600 ± 447151.591 ns/op
LookupStringsBenchmark.JavaTree ss 10 7279490.300 ± 667739.355 ns/op
LookupStringsBenchmark.BigBTree3 ss 10 12567509.100 ± 1215372.374 ns/op
LookupStringsBenchmark.BigBTree10 ss 10 11546350.200 ± 727266.401 ns/op
LookupStringsBenchmark.BigBTree100 ss 10 11678035.600 ± 644743.258 ns/op
LookupStringsBenchmark.BigBTree1000 ss 10 11077497.900 ± 928992.874 ns/op
LookupStringsBenchmark.BigJavaTree ss 10 10295538.600 ± 926229.417 ns/op
Видно, что на малых деревьях преимущество за B-Tree, а вот начиная с ~100к ключей он сдувается и доминировать начинает TreeSet.
Выводы
Наивная реализация B-Tree в Java показывает приемлемые результаты - как минимум асимптотическая сложность остаётся на уровне бинарного дерева, хотя производительность в ns/op несколько ниже при размере дерева от 100к ключей. Не merge sort VS quick sort конечно, но что есть, то есть. Что интересно, B-Tree в большинстве случае требует на себя меньше памяти, чем обычное дерево (см. фрагмент текста про оптимизацию памяти). И выделяет её бОльшими фрагментами.
Похоже, что ставка на меньшее число случайных чтений отчасти сыграла, но нивелируется по мере роста количества ключей за счёт меньшего количества сравнений, выполняемого TreeSet стандартной библиотеки.
Ну и наверное логичным выводом из этого всего будет то, что в условиях дешёвого чтения (все данные помещаются в оперативке или быстром кеше) выгоднее использовать обычное бинарное дерево. Исключение - если нужно сэкономить память. B-Tree скорее более экономичен в плане расходов на внутреннюю структуру.
That's all folks! Спасибо за внимание.
Собеседовательное
Настоящее практическое применение
Ладно, чиселки перекладывать оно умеет, а помогает ли это знание в перекладывании грОшей от работодателя работнику? Иначе говоря, что там на собеседованиях? Нужное знание-то? Делюсь своим опытом, оставляю опрос, чтобы читатель мог поделиться своим.
До недавнего времени я был уверен, что B - это про BST. Из N собеседований на позицию веб разработчика, которые я прошёл за последние 10 лет, я был спрошен об индексах буквально каждый раз и в N - 2 случаях даилог выглядел примерно так:
Собеседующий (С): А вот сделали мы табличку в БД и нам не нравится производительность определённых запросов, что делаем?
Я: Делаем explain analyze, добавляем простой или композитный индекс, чтобы ограничить область поиска перебором.
С: О, индекс, а что за индекс?
Я: В 99% случае это B-Tree, в СУБД есть другие виды, но их на практике видно редко. B-Tree - это бинарное балансированное дерево поиска, поиск за logn.
С: Окей, тут хватит, переходим к ...
Но один раз ответ "прокатил" не полностью:
...
Я: В 99% случае это B-Tree, в СУБД есть другие виды, но их на практике видно редко. B-Tree - это бинарное балансированное дерево поиска, поиск за logn.
С: На самом деле это не бинарное дерево. Дерево - да, балансированное - да, поиска - да, бинарное - нет, у каждой ноды больше 2 потомков. Там всё интереснее, ознакомьтесь, товарищ соискатель.
Я: о_О. Ок, интересно, спасибо, посмотрю.
Ну что же, ознакомился, век живи, век учись, всё равно дураком помрёшь, но следующее собеседование из-за этого получилось ещё интереснее:
...
Я: В 99% случае это B-Tree, в СУБД есть другие виды, но их на практике видно редко. B-Tree - это небинарное балансированное дерево поиска.
С: Что значит небинарное?
Я: В узлах дерева может быть множество ключей, причём для БД используются деревья с буквально огромными узлами, чтобы минимизировать запросы к файловой системе - в хорошем случае вообще верхние уровни дерева хранятся в оперативке, нижний-е лежат на диске.
С: Что-то ты перемудрил, это ерунда какая-то. Индекс - это балансированное бинарное дерево, направо-налево-направо и нашёл, а если ключи массивом в узле это медленно.
Я: О_о. Ок, бинарное так бинарное, ну тогда это бинарное балансированное дерево, поиск за logn.
С: Ну вот, хорошо, тут хватит, переходим к...
На результат собеседования не повлияло, но вот, бывает и так.
Автор: ivan_evgrafov






