«Невозможный» параллельный алгоритм неотрицательной суммы

Сумма целых чисел — что может быть проще? Сумма есть в SQL, в Java Stream API… в крайнем случае напишем сами. Как и всякая абстракция, она расходится с реальностью.

Вот счёт клиента в банке, по нему движения — положительные пополнения и отрицательные списания — в сумме дают текущий баланс. Так сумма работает в идеальном мире. А в реальности при большом минусе банк с отсрочкой, но предпримет нетривиальные действия вплоть до обращения в суд, чтобы закрыть финансовую брешь.

static long usualSum(LongStream changes) {
    return changes.reduce(0, (a, b) -> a + b);
}

Для склада вроде бы те же положительные приходы и отрицательные отгрузки в сумме дают текущий остаток. Но действия по увязке абстракции с реальностью придётся предпринимать безотлагательно — нельзя отгрузить товар, которого физически нет, нужно сразу считать неотрицательную сумму, поправляя отгрузку. Это касается всех материально-физических объектов — хоть наличных в кошельке, хоть овец в стаде.

static long nonNegativeSum(LongStream changes) {
    return changes.reduce(0, (a, b) -> Math.max(0, a + b));
}

А здесь уже проблемы реализации:

• Неассоциативная бинарная операция нарушает контракт свёртки Stream.reduce(). При вычислении после Stream.parallel() результат будет некорректным, отличным от результата последовательного вычисления.

• Внутри Math.max() есть ветвление и заранее неизвестно, хватит ли остатка на складе для отгрузки. Как разбить вычисление на независимые куски для параллельных вычислителей, если следующий кусок последовательно зависит от предыдущего?

• В SQL нет аналога, а пользовательский агрегат, опять же, должен быть ассоциативным для параллелизации.

"Невозможная" параллельная реализация неотрицательной суммы всё же существует. Весь немногословный код поместим в

public class Example {
    …
}

Для тестирования создадим длинную историю псевдослучайных изменений, пусть распределённых на отрезке [-99, 99]

static LongStream changes() {
    return LongStream
            .range(1, 1000_000_000)
            .map(i -> (i * 137) % 199 - 99);
}

Чтобы на коленке оценить корректность и эффект от параллелизации, печатаем время вычисления и результат.

static void bench(ToLongFunction<LongStream> function, LongStream changes) {
    long start = System.currentTimeMillis();
    long result = function.applyAsLong(changes);
    long end = System.currentTimeMillis();
    System.out.printf("%4sms: %sn", end - start, result);
}

Проверим обычную сумму: вычисления параллелятся идеально и результат совпадает с последовательным. Догадайтесь, сколько ядер в процессоре?

bench(Example::usualSum, changes());
bench(Example::usualSum, changes().parallel());
> 1585ms: 147
>  390ms: 147

Наивная реализация считается быстро, но неправильно при параллельном вычислении.

bench(Example::nonNegativeSum, changes());
bench(Example::nonNegativeSum, changes().parallel());
> 1274ms: 300
>  390ms: 13309

Для верного параллельного решения познакомимся с группой Гротендика, которая позволяет представить целое, в том числе отрицательное, парой натуральных чисел

-2 ~ (5, 3) ~ (15, 13) ~ (105, 103) ~ …

где первый элемент пары трактуется как вычитаемое, а второй элемент — как уменьшаемое. Класс с двумя полями в представлении Гротендика будет хранить промежуточное состояние агрегата неотрицательной суммы.

static final class Gro {
    private long fall;
    private long grow;
}

Место для удара головой 🤯

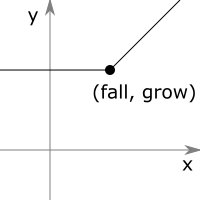
Семейство функций смещённых ReLU с двумя параметрами fall и grow, задающих точку излома, замкнуто относительно композиции. То есть y₂(y₁(x)) имеет такой же вид смещённого ReLU, ибо

max(0, a + max(0, b)) = max(0, a) + max(0, b + min(0, a))

Композиция функций ассоциативна, значит, композиция смещённых ReLU тоже ассоциативна.

Неотрицательную сумму реализуем через мутабельную свёртку Stream.collect():

• Параллельным вычислителям раздаём по пустому агрегату Gro::new;

• Агрегируем accumulator независимые куски данных;

• В конце попарно, сохраняя порядок кусков, объединяем через combiner агрегаты всех вычислителей в один.

• Результатом из объединённого агрегата достаём только уменьшаемое, а про вычитаемое забываем.

  static long grosum(LongStream changes) {
      return changes.collect(Gro::new, Example::accumulator, Example::combiner)
        					  .grow;
  }
  
  static void accumulator(Gro a, long value) {
      a.grow += value;
      if (a.grow < 0) {
          a.fall -= a.grow;
          a.grow = 0;
      }
  }
  
  static void combiner(Gro a, Gro b) {
      if (a.grow < b.fall) {
          a.fall += b.fall - a.grow;
          a.grow = b.grow;
      } else {
          a.grow += b.grow - b.fall;
      }
  }

Проверяем параллельную реализацию неотрицательной суммы: вычисления параллелятся отлично и результат совпадает с последовательным.

bench(Example::grosum, changes());
bench(Example::grosum, changes().parallel());
> 1277ms: 300
>  402ms: 300

select grosum(change) over (order by time) as balance
from changes

prop_eq xs  = grosum xs == foldl' (⊞) 0 xs
prop_monoid = monoid (mempty :: Gro Int)

Какая-то абстрактная магия в реальности работает на благо человека.