У меня возникла необходимость вычислять в Java-приложении значения формул, вводимых пользователями (да еще и так, чтобы приложение понимало комплексные числа). Внимание сразу привлекла библиотека Jep, но ввиду определенных ограничений использовать ее не представилось возможным. Поэтому я решил написать свой парсер, используя Алгоритм Дейкстры для преобразования входной записи из инфиксной нотации в постфиксную, также известный, как Алгоритм сортировочной станции. Он довольно прост, но в то же время элегантен, и я получил удовольствие, реализовывая его. Заинтересовавшихся — прошу под кат.
Нотации
Начну с начала. Математические выражения можно записывать в трех основных формах: префиксной (польская нотация aka Polish Notation, PN), инфиксной и постфиксной (обратной польской нотации aka ПОЛИЗ aka Reverse Polish Notation, RPN). Например, представленные ниже формулы эквивалентны:
- infix: (5 — 6) * 7
- PN: * — 5 6 7
- RPN: 5 6 — 7 *
Одним из стандартных решений задачи парсинга мат. выражений является перевод их из инфиксной записи в постфиксную, поскольку выражения, записанные в последней, очень легко вычислить, используя т. н. «стековую машину» — алгоритм, проводящий вычисления по обратной польской записи. Для перевод infix → RPN можно использовать ряд алгоритмов, но, как я уже говорил в начале статьи, речь пойдет именно о shunting-yard algorithm.
Алгоритм сортировочной станции
Подготовка
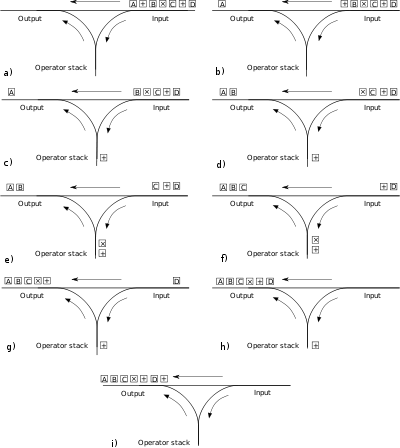
Эдсгер Дейкстра назвал его именно так из-за сходства в принципе действий с обычной железнодорожной сортировочной станцией.
Для перевода между нотациями используется стек и выходная очередь. Входная строка разбивается на токены. Считывание входной строки происходит по одному токену и в зависимости от того, к какой категории он относится, происзводится одно из возможных действий.
Категории варьируются от одной реализации к другой, основная проблема стоит вокруг скобок — некоторые их относят к операторам, некоторые к разделителям, кто как. Я выделяю их в отдельную категорию — «скобки».
Далее самой очевидной категорией является «числа». Хочу отметить, что число, естественно, может быть как целым, так и дробным, однако дробная запись должна быть в десятичной форме, т. к. запись «1/3» не означает число «одна третья» — она означает выражение «один разделить на три». Также в моем случае в данную категорию необходимо было добавить комплексные числа, т. е. содержащие в своей записи мнимую единицу. О том, как я это сделал, будет сказано чуть позже.
Самой простой категорией является «разделители» аргументов функций нескольких переменных (например, функция pow). В моей реализации в эту категорию входит единственный символ — запятая.
Категория «функции». Тут все просто: это список доступных для понимания вашего парсера математических функций, таких как sin, exp, abs и т. д.
И, напоследок, «операторы». Операторами в данном контексте принято называть символы: + — * / и иногда ^ Однако, вы можете определять собственные операторы, например, точку — для перемножения матриц (тогда вам также необходимо определить специальную категорию для матриц). Каждый оператор мы рассматриваем с точки зрения двух интересующих нас параметров: приоритет и ассоциативность — мы знакомы с этими понятиями со школы.
Пожалуй, это вся базовая информация, которая нас интересует, можно перейти к алгоритму.
Собственно, алгоритм
Чтобы не повторяться, скопирую его с Википедии (ссылка на статью в начале топика):
Пока не все токены обработаны:
- Прочитать токен.
- Если токен — число, то добавить его в очередь вывода.
- Если токен — функция, то поместить его в стек.
- Если токен — разделитель аргументов функции (например запятая):
Пока токен на вершине стека не открывающая скобка, перекладывать операторы из стека в выходную очередь. Если в стеке не было открывающей скобки, то в выражении пропущен разделитель аргументов функции (запятая), либо пропущена открывающая скобка.- Если токен — оператор op1, то:
Пока присутствует на вершине стека токен оператор op2, и
Либо оператор op1 лево-ассоциативен и его приоритет меньше чем у оператора op2 либо равен,
или оператор op1 право-ассоциативен и его приоритет меньше чем у op2,
переложить op2 из стека в выходную очередь;
положить op1 в стек.- Если токен — открывающая скобка, то положить его в стек.
- Если токен — закрывающая скобка:
Пока токен на вершине стека не является открывающей скобкой, перекладывать операторы из стека в выходную очередь.
Выкинуть открывающую скобку из стека, но не добавлять в очередь вывода.
Если токен на вершине стека — функция, добавить ее в выходную очередь.
Если стек закончился до того, как был встречен токен открывающая скобка, то в выражении пропущена скобка.- Если больше не осталось токенов на входе:
Пока есть токены операторы в стеке:
Если токен оператор на вершине стека — открывающая скобка, то в выражении присутствует незакрытая скобка.
Переложить оператор из стека в выходную очередь.Конец.
Если читатель знаком с таким понятием, как конечный автомат, то понять алгоритм для него не составит труда. Если нет, то стоит ознакомиться.
Реализация на Java
Прошу не пинать сильно за кривой код — не было времени как следует все оптимизировать, обязательно займусь этим вскоре. Итак, приступим.
Создадим класс, который назовем, как душе угодно. В него поместим следующие поля (пардон за мой французский в комментариях к коду):
// list of available functions
private final String[] FUNCTIONS = { "abs", "acos", "arg", "asin", "atan", "conj", "cos", "cosh", "exp", "imag", "log", "neg", "pow", "real", "sin", "sinh", "sqrt", "tan", "tanh" };
// list of available operators
private final String OPERATORS = "+-*/";
// separator of arguments
private final String SEPARATOR = ",";
// imaginary symbol
private final String IMAGINARY = "I";
// variable token
private final String VARIABLE = "var";
// temporary stack that holds operators, functions and brackets
private Stack<String> stackOperations = new Stack<String>();
// stack for holding expression converted to reversed polish notation
private Stack<String> stackRPN = new Stack<String>();
// stack for holding the calculations result
private Stack<String> stackAnswer = new Stack<String>();
Далее нам необходимо определить ряд вспомогательных методов, которые нам будут нужны по ходу дела:
private boolean isNumber(String token) {
try {
Double.parseDouble(token);
} catch (Exception e) {
if (token.contains(IMAGINARY) || token.equals(VARIABLE)) {
return true;
}
return false;
}
return true;
}
private boolean isFunction(String token) {
for (String item : FUNCTIONS) {
if (item.equals(token)) {
return true;
}
}
return false;
}
private boolean isSeparator(String token) {
return token.equals(SEPARATOR);
}
private boolean isOpenBracket(String token) {
return token.equals("(");
}
private boolean isCloseBracket(String token) {
return token.equals(")");
}
private boolean isOperator(String token) {
return OPERATORS.contains(token);
}
private byte getPrecedence(String token) {
if (token.equals("+") || token.equals("-")) {
return 1;
}
return 2;
}
Обратите внимание на метод isNumber — он характеризует, как число, любой токен, содержащий символ мнимой единицы, а также токен, который является переменной (для простоты парсер поддерживает задание одной переменной — «var»).
И теперь, собственно, основной метод нашего класса:
public void parse(String expression) throws ParseException {
// cleaning stacks
stackOperations.clear();
stackRPN.clear();
// make some preparations
expression = expression.replace(" ", "").replace("(-", "(0-")
.replace(",-", ",0-");
if (expression.charAt(0) == '-') {
expression = "0" + expression;
}
// splitting input string into tokens
StringTokenizer stringTokenizer = new StringTokenizer(expression,
OPERATORS + SEPARATOR + "()", true);
// loop for handling each token - shunting-yard algorithm
while (stringTokenizer.hasMoreTokens()) {
String token = stringTokenizer.nextToken();
if (isSeparator(token)) {
while (!stackOperations.empty()
&& !isOpenBracket(stackOperations.lastElement())) {
stackRPN.push(stackOperations.pop());
}
} else if (isOpenBracket(token)) {
stackOperations.push(token);
} else if (isCloseBracket(token)) {
while (!stackOperations.empty()
&& !isOpenBracket(stackOperations.lastElement())) {
stackRPN.push(stackOperations.pop());
}
stackOperations.pop();
if (!stackOperations.empty()
&& isFunction(stackOperations.lastElement())) {
stackRPN.push(stackOperations.pop());
}
} else if (isNumber(token)) {
if (token.equals(IMAGINARY)) {
stackRPN.push(complexFormat.format(new Complex(0, 1)));
} else if (token.contains(IMAGINARY)) {
stackRPN.push(complexFormat.format(complexFormat.parse("0+"
+ token)));
} else {
stackRPN.push(token);
}
} else if (isOperator(token)) {
while (!stackOperations.empty()
&& isOperator(stackOperations.lastElement())
&& getPrecedence(token) <= getPrecedence(stackOperations
.lastElement())) {
stackRPN.push(stackOperations.pop());
}
stackOperations.push(token);
} else if (isFunction(token)) {
stackOperations.push(token);
}
}
while (!stackOperations.empty()) {
stackRPN.push(stackOperations.pop());
}
// reverse stack
Collections.reverse(stackRPN);
}
Щепотка пояснений, т.к. код, думаю, довольно тривиальный. Вначале мы выполняем небольшую подготовку выражения: убираем все пробелы, а также устраняем проблему со знаком минус. Проблема заключается в том, что минус может выступать не только как бинарный оператор, но и как унарный — для записи отрицательных чисел. Поэтому нам нужно контроллировать случаи, когда он встречается в начале строки или сразу же после открывающейся скобки. В принципе, то же самое можно предусмотреть и для плюса, но кто в здравом уме будет намеренно дописывать плюс перед положительным числом?
Далее с помощью стандартного класса StringTokenizer разбиваем входную строку на токены. Очень удобный Java-класс, не пришлось писать свой. И далее запускаем основной цикл алгоритма.
В нескольких местах вы можете встретить упоминание экземпляра класса ComplexFormat. Это класс из библиотеки Apache Commons Math, которую я использую для дальнейшего вычисления результата выражения, что, в принципе, не является темой данного топика (о вычислении значения RPN-выражения можно почитать тут).
Заключение
В принципе, вот и все. Еще раз повторюсь, что нахожу этот алгоритм довольно элегантным (вообще люблю Дейкстру и его алгоритмы — величий информатик). Работа над этим вылилась в создание open-source библиотеки Bracer: bracer.sourceforge.net
Буду рад услышать конструктивную критику и предложения. Надеюсь, статья поможет кому-то, кто столкнулся с данной задачей в своем проекте, или просто нерадивому студенту, которому лень разбираться с теорией для лабораторной работы самостоятельно. Спасибо за внимание!
Автор: NirvanaGhost
