Данная статья написана в силу возмущения тем, что в наших ВУЗах студентов простому разбору математических выражений обучают на основе как раз Обратной Польской Нотации (ОПН), что является откровенным извращением нормальной человеческой логики.
Источником описания ОПН будет описание из Лафоре Р.: Л29 Структуры данных и алгоритмы в Java. Классика Computers Science. 2-е изд. — СПб.: Питер, 2013. — 704 с, рекомендованное как наиболее популярное и адекватное по этому вопросу, впрочем как и по другим часто применяемым алгоритмам.
Ну то есть сравниваем разные алгоритмы с разной идеологией.
Для визуализации последовательности работы над формулой (ОПН) на стр.158 приведён следующий граф:
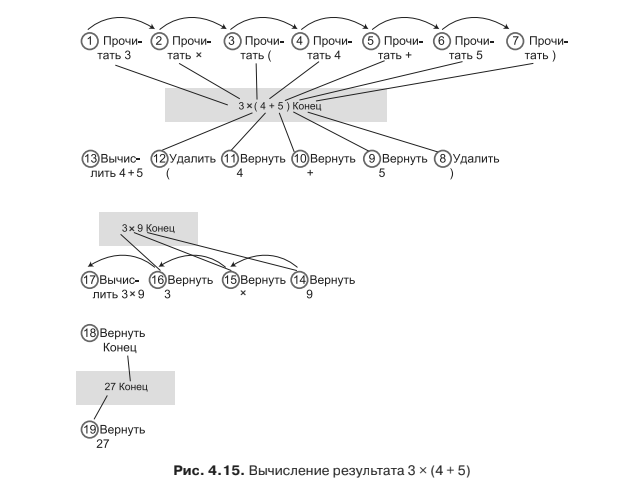
Уже здесь можно увидеть подстраивание алгоритма под неверное для человека свойство последовательного считывания символьной информации. Для человека более характерно приоритетное выделение фрагментов выражения и построение дальнейшей схемы расчётов по приоритетам этих фрагментов. Поэтому в данном случае схема будет выглядеть в реальности вот так:
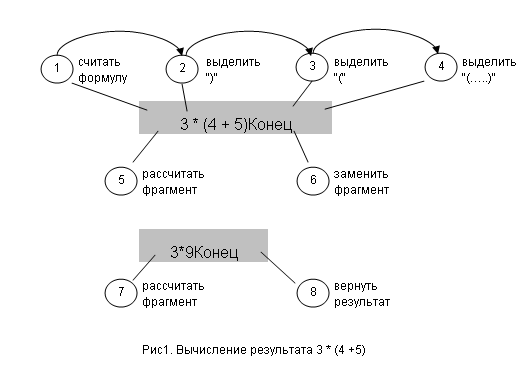
Как видим, неверный исходный посыл на посимвольный разбор выражения приводит не только к искажению обработки инфиксной записи, но и существенно усложняют картину реального разбора сложных формул с множественными вложениями скобок. Ведь вторая схема (Рис1) и понятнее и существенно короче, чем представлено на Рис.4.15 анализируемого источника.
Далее я вынужден привести достаточно пространную цитату из источника, в которой «сову натягивают на глобус».
«Как видите, в процессе вычисления результата инфиксного арифметического выражения приходится перемещаться по выражению в прямом и обратном направлениях. Сначала слева направо читаются операнды и операторы. При накоплении информации, достаточной для применения оператора, вы начинаете двигаться в обратном направлении, «вспоминаете» два операнда и оператор и выполняете арифметическое действие. Если за оператором следует другой оператор с более высоким приоритетом или скобки, применение оператора откладывается. В этом случае сначала применяется следующий, более приоритетный оператор, а затем вы возвращаетесь обратно (влево) и применяете более ранние операторы.
Конечно, алгоритм для выполнения подобной обработки можно было бы запрограммировать напрямую, и все же, как уже говорилось ранее, проще сначала преобразовать выражение к постфиксной записи.» (конец цитаты)
Начнём с перемещения в прямом и обратном направлении. Дело в том, что апологеты ОПН обычно делают упор на последнем этапе расчётов, когда уже пересортированные символы сложены в стек и извлекаются оттуда подряд, что конечно же делает этот этап очень эффективным, вроде как. Но ведь, как помним работа по ОПН состоит из ДВУХ этапов (стр. 153):
«1. Преобразование арифметического выражения в другой формат, называемый постфиксной записью.
2. Вычисление результата по постфиксной записи.» (конец цитаты)
Упс! Оказывается преимущества второго этапа стараются выпятить, а вот головную боль с этапом первым просто скромно упоминают вскольз. Это не упрёк автору, автор пишет классно – это непонимание почему данный, достаточно мутный, метод считается основным при разборе формул и преподаётся на соответствующих специальностях.
Однако давайте посмотрим внимательно на этап первый. Благо автор предоставляет для этого шикарную таблицу (стр. 153):
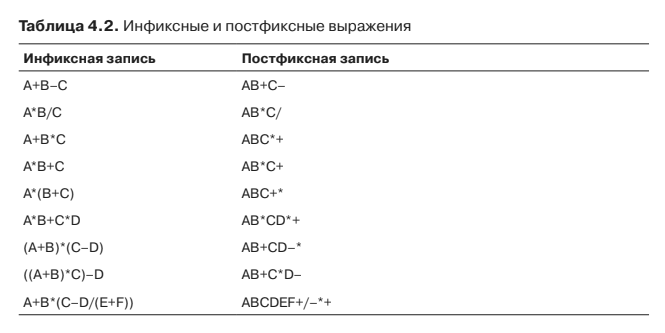
Больше всего мне понравилась последняя строчка. Вот расскажите, ради бога, как это можно здесь последовательно вытаскивать из СТЕКА и получать вменяемый результат. Система из двух стеков, отдельно для операндов и отдельно для операций, ещё будет работать, а вот с одним стеком…
Но речь даже не об этом. Сколько и каких сортировок нужно сделать, чтобы из инфиксной (привычной нам) записи сделать постфиксную? К чему так ломать нормальную человеческую логику студентов в угоду древнего метода? Боюсь даже представить как будет выглядеть, например, такая формула: (A+B*C/D)+(E-F*((G/(H-J*(-1)+I)-L*(M-N)-R)+S). А у вас получилось представить это сходу?
Таким образом можно сказать что само преобразование из инфиксной в постфиксную запись уже несёт в себе неоправдано большие затраты на реализацию сложных слабопонятных алгоритмов сортировки исходных данных. Причём количество возвратов на этом этапе явно будет превышать ресурсы, требуемые на обработку инфиксной (нормальной) записи. Ну и обработка самой такой постфиксной записи, как-то не ограничивается примитивным вытаскиванием подряд из стека, а требует соответствующего обработчика и дополнительных ресурсов.
Проиллюстрируем последовательность требуемых операций (ОПН) на небольшом примере.

Табл1. Порядок расчёта фрагмента формулы
Но и это ещё не всё, ведь если числа состоят не из одной цифры, то надо ставить буфер для сборки числа из отдельных цифр перед помещением их в стек или выходную строку.
У меня нет задачи пересказывать метод расчёта ОПН, поэтому те, кому особо интересно, могут прочитать о нём в первоисточнике, тем более что он действительно классно написан. Посему перейдём к методу (алгоритму) Пинг-Понг, анонсированному в названии статьи.
Сразу оговорюсь, методов (алгоритмов) распарсивания формул достаточно много. Можно назвать и метод рекурсивного спуска и методы построения деревьев и другие. Пинг-Понг мною в сети найден не был, хотя, так думаю, его используют достаточно часто. Почему он получил такое название станет ясно из иллюстраций.
Итак, переходим к разбору алгоритма. Начнём с некоторых определений для удобства изложения.
Приоритет – доминирование одной операции или группировки над другими. В алгоритме используются три приоритета: 0 – операции « ±»; 1 – операции «*/%»; 2 – группировка круглыми скобками «( )». Примечание: функции и работа с ними в данной статье не рассматриваются. Функции – просто отдельный слой, который не оказывает влияния на приоритетность выполнения операций.
Фрагмент – часть формулы, которая может быть передана для более низкоуровневого расчёта. То есть фрагментом является как часть формулы обрамлённая скобками и содержащая операции 0-го и 1-го уровней, так и тривиальный фрагмент, содержащий два операнда и знак операции между ними.
Для удобства иллюстрации будем использовать ту же формулу, которая была предложена выше для расчёта по ОПН: (A+B*C/D)+(E-F*((G/(H-J*(-1)+I)-L*(M-N)-R)+S)*W). Чтобы было более наглядно в процессе иллюстрации работы алгоритма я буду заменять буквы на цифры. Поехали.
Имеем строку формулы на входе.

Операнды вытаскиваются относительно знака операции, один слева другой справа. Последовательность операций внутри фрагмента напрямую зашита приоритетом последовательности обработки с замещением результатом. Вопросы унарного и бинарного « — » решаются внутри блока сложения/вычитания.
Так думаю, что здесь даже и не надо много разъяснений. Ну и так же понятно откуда название. Как видим, сортировки отсутствуют как класс, ограничений на длину формулы и количества вложенных групп — нет. Всё на уровне тривиальных поисков и замен. Чтобы не плодить обрывки строк, достаточно вместо String использовать StringBuilder (java), который позволяет трансформировать строку не плодя лишних сущностей. Ну а главное – это всё понятно на уровне простого интуитивного восприятия.
Для сравнения алгоритмов представим их в одинаковой нотации.
Алгоритм для ОПН взят из Wiki
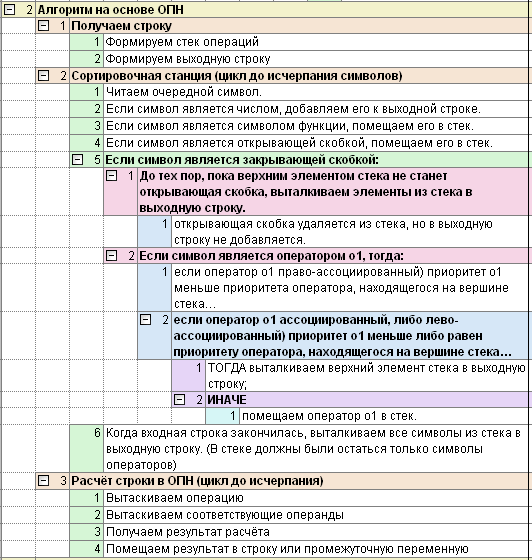
Алгоритм Пинг-Понг
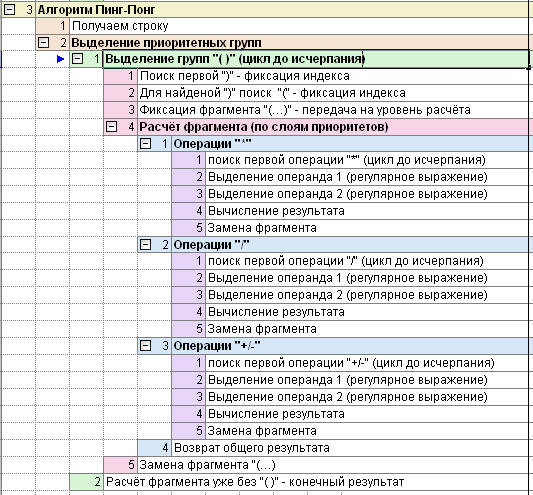
Таким образом алгоритм Пинг-Понг максимально приближен к человеческому восприятию и требует минимального количества ресурсов. Он также по минимуму требует анализа символов и процедур выбора решения, не требует буфера для сборки чисел из цифр.
Таких интуитивно понятных алгоритмов, думаю, достаточно много. Так почему же студентов до сих пор мучают всякой хренью, придуманой в незапамятные времена?
Буду рад если кому-то этот алгоритм пригодится.
Автор: valerar






